探究性教学模式融入二次函数教学的策略探讨

华德

摘要：在深化基礎教育改革的背景下，如何在数学教学中落实素质教育理念，是数学教师关注的焦点。对此，教育工作者认为，探究性教学模式在落实素质教育方面具有明显优势，可应用于数学教学中。文章以初中二次函数教学为例，探究探究性教学模式融入教学中的策略，即优化概念课程、图像与性质课程、应用课程，以此建构探究性二次函数知识学习新格局，让学生深入掌握二次函数知识，并灵活应用二次函数知识。

关键词：初中数学；探究性教学模式；二次函数；概念；应用

中图分类号：G633.6文献标志码：A文章编号：1008-3561（2022）17-0086-03

新课标对二次函数的教学内容、教学目标有详细、具体要求。在具体教学中，教师要积极引导学生理解公式推导过程，然后在此基础上让学生确定二次函数的解析式，充分掌握二次函数的基本性质、基本定理、与二次函数相关的思维方法等，由此提升学生的抽象概括能力、推理论证能力、处理分析数据能力，为学生数学核心素养的持续发展奠定良好基础。另外，二次函数内容在中考出现的几率很大，在未来的高中学习中，学生还要继续探究二次函数知识，因此在初中阶段奠定良好的二次函数知识基础非常有必要。由此可见，二次函数是初中数学教学的重点和难点，教师应结合二次函数的实际学情，积极优化教学策略，引导学生深度探究二次函数知识，构建理想的知识学习和应用格局。

一、探究性教学模式融入二次函数教学的意义

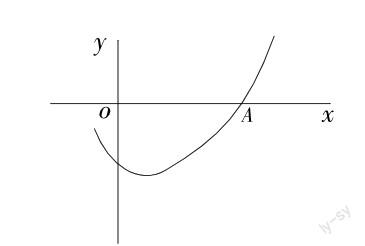
传统的二次函数知识教学多以教师的演示推导为主，学生的自主性难以体现，课堂探究性特征也不明显，显然这不利于学生深度理解二次函数知识，并有可能导致部分学生陷入学困状态。为有效规避这一教学风险，教师可在二次函数教学中融入探究性教学模式。探究性教学模式是以研究数学问题为主的课堂教学活动，在此过程中，教与学的关系得到极大改善，学生成为课堂主人，其通过相互探讨，积极发现问题、分析问题、解决问题，并以此激活数学思维，进入深度理解、应用二次函数知识的最佳状态。例如，下图是二次函数y=ax2+bx+c（a≠0）图像的一部分，且过点A（3，0），二次函数图像的对称轴是直线x=1，下列结论正确的是（）。A.b2<4ac，B.ac>0，C.2a-b=0，D.a原b垣c=0。上述题设考查的是二次函数图像与系数的关系，要求学生在深度理解函数图像与系数关系的基础上，巧妙结合题设条件进行解题。与此类似的题设是中考常见的考查内容，这就要求学生深度理解二次函数知识，然后在此基础上结合实际题设，迅速找到解决问题的方案，得到正确答案。二次函数知识涉及很多变量，具有不确定性，在解答的时候，学生要有探究的意识，才能渐入佳境。由此可见，探究性教学模式融入二次函数教学中非常有必要，可以建构探究性的二次函数知识学习格局，为后续二次函数知识的应用奠定基础。

二、探究性教学模式融入二次函数教学中的策略

初中二次函数的知识点比较多，学生如果理解得不透彻将直接影响到后续的应用。为此，教师要深入探究探究性教学模式融入二次函数的策略，不断提升二次函数的教学质量。

1.基于探究性教学的二次函数概念课程优化

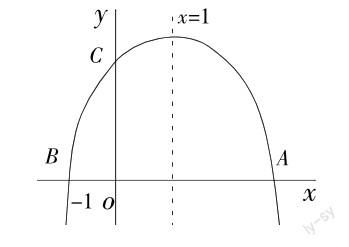
对学生二次函数概念理解情况的调研显示，部分学生对二次函数概念的理解停留在机械性记忆层面，没有真正与解析式y=ax2+bx+c（a≠0）关联起来，也就是说概念理解处于浅层状态。另外，部分学生对上述公式中各项系数取值范围的理解是死记硬背的，并且在解题的时候容易忽视a≠0。二次函数的概念本身比较抽象、复杂，学生理解起来很吃力，部分学生的抽象思维能力不强，而有的教师在教学二次函数概念的时候，以灌输的方式为主，让学生以背诵的方式理解解析式，导致二次函数的教学处于低效化的状态。

在此版块的教学中，探究性教学模式的嵌入，可将焦点放在如下几个方面。第一，积极获取生活化素材，让学生根据生活化素材对二次函数形成初步感知。例如，教师可在课堂导入阶段播放一段CBA的比赛视频，引导学生将熟悉的篮球运动与抛物线关联起来。在熟悉的生活情境中思考二次函数，学生可将自己的积极情绪融入教学中。第二，引导学生在生活经验的基础上，形成二次函数的概念。为此，教师可以引入一些生活案例：（1）正方形的表面积与边长之间的关系是什么样的？（2）老师将积攒下来的2万元钱存入银行，已经知道实际的年利率为x，两年后老师的存款有多少？（3）一个矩形的长和宽分别为30米、20米，如果长和宽都向外面扩x米，请问此时形成的矩形面积是多少？……结合上述案例，教师可引导学生思考变量x与y之间的关系，继而得出二次函数的定义，并鼓励学生对自己不理解的内容大胆质疑。第三，结合学生的反馈，引导学生进行针对性的探究。例如，对于学生不理解的为什么a的取值不能等于0，就可让学生尝试将a的取值设定为0，再去推导。这时，学生会发现如果a等于0，那么解析式就不是二次函数，两个变量之间的关系也不成立。但如果a等于0，两个变量之间还是一次函数关系，同样可以归结为一次函数。在回忆上述二次函数知识的基础上，教师可引导学生总结二次函数，以此加深学生的理解。第四，结合学生的探讨情况引入针对性的习题。例如，如下图，二次函数y=ax2+bx+c（a≠0）的图像与x轴交于A、B两点，与y轴交于C点，且对称轴为x=1，点B坐标为（-1，0），则下面的4个结论：①2a+b=0、②4a原2b+c<0、③ac>0、④当y<0时，x<-1或x>2，其中正确的个数是（）。A.1个，B.2个，C.3个，D.4个。