带有导子的n-李代数形变
2022-05-30徐江南
徐江南,杜 磊
(安徽大学 数学科学学院,安徽 合肥 230601)
0 引 言
代数形变理论最先由Gerstenhaber提出,在文献[1]中,Gerstenhaber介绍了结合代数的形变.自Gerstenhaber之后,各种代数结构的形变开始被许多学者研究[2-6].1966年,Nijenhuis和Richardson研究了分次李代数的形变[2];2004年,Yau研究了余代数代数同态的形变[3];2019年,Tang等构造李代数带有导子的上同调,并用其研究了一些问题[4];2021年,Sun等构造n-李代数带有导子的上同调,讨论了n-李导子对的上同调与相应莱布尼兹导子对的上同调之间的关系,定义了近似形变,并研究了Nijenhuis算子和O-算子与n-李导子对之间的关系[5].本文主要对n-李代数带有导子的形变进行更深入的研究.
1 预备知识
下面简单回顾n-李代数的相关概念及其用到的两个上链复形.
对任意的σ∈Sn,定义sgn(σ)为σ的符号,即若σ为奇置换,则sgn(σ)=-1;若σ为偶置换,则sgn(σ)=1.设V是域上的线性空间,k为任意正整数,定义⊗kV为k个V的张量积.
定义1[7]一个n-李代数是指一个线性空间N,以及N上一个n-元多重线性映射[·,…,·]:⊗nN→N,且该线性映射满足以下等式:
[x1,…,xn]=sgn(σ)[xσ(1),…,xσ(n)],
(1)
(2)
对任意的σ∈Sn和xi,yj∈N均成立.
定义2[7]n-李代数(N,[·,…,·])的一个导子是指一个线性映射D:N→N满足以下条件:
(3)
对任意的x1,…,xn∈N.定义Der(N)为n-李代数(N,[·,…,·])的所有导子构成集合.
定义3设N是一个n-李代数,D是N的一个导子,称(N,D)为一个n-李导子对.
设(N,[·,…,·])是一个n-李代数.下面介绍n-李代数以自身为系数的上同调复形.为使上同调复形形式更简洁,先定义一些映射.定义线性空间∧n-1N为L(N),定义线性映射ad:L(N)∧N→N,双线性映射[ , ]:L(N)×L(N)→L(N)分别为:
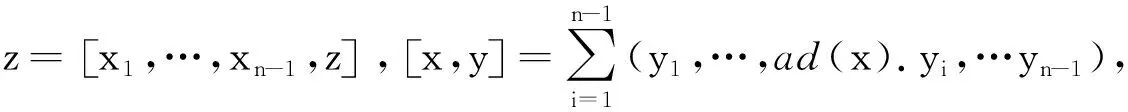
对任意的x=x1∧…∧xn-1∈L(N),y=y1∧…∧yn-1∈L(N),z∈N.
定义4[8]设(N,[·,…,·])是一个n-李代数,则N以自身为系数的上同调,定义为Hp(N),是上链复形C*(N,N)的上同调群.其中,C*(N,N)定义如下:C*(N,N)的0-上链定义为0,对p≥0,C*(N,N)的(p+1)-上链为所有的线性映射f:⊗pL(N)∧N→N.定义C*(N,N)的(p+1)-上链为Cp(N,N).C*(N,N)的微分dp+1:Cp(N,N)→Cp+1(N,N)定义如下:
dp+1f(a1,…,ap,ap+1,z)=
(4)

为方便起见,下面将省略微分dp+1的上标,用d来代替dp+1.
设(N,[·,…,·])是一个n-李代数,D是它的一个导子.为使上链复形的微分运算更简洁,先定义一些算子:
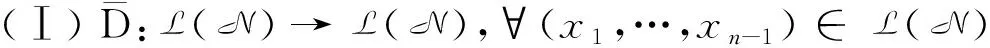
(5)
(Ⅱ)δ:Cp(N,N)→Cp(N,N),∀f∈Cp(N,N),ai∈L(N),z∈N定义为:

(6)
定义控制导子形变的复形为C*(N,D).C*(N,D)的各项定义如下:
对任意的p≤0,
Cp(N,D)=0.
对任意的p≥2,
C1(N,D)=C1(N,N)=Hom(N,N),
Cp(N,D)=Cp-1(N,N)×Cp-2(N,N).
下面定义C*(N,D)上的微分算子.
对p=1,定义∂:C1(N,D)→C2(N,D)为:
∂f=(df,(-1)1δf),∀f∈C0(N,N).
对p≥2,定义∂:Cp(N,D)→Cp+1(N,D)为:
∂(f,g)=(df,dg+(-1)pδf),∀f∈Cp-1(N,N),g∈Cp-2(N,N).
定理1[5](C*(N,D),∂)是一个复形.
2 n-李代数带有导子的形变
设(N,D)是一个n-李导子对,考虑一族线性映射:
[·,…,·]t=∑i≥0[·,…,·]iti,Dt=∑i≥0Diti,
其中,[·,…,·]i∈C1(N,N),[·,…,·]0=[·,…,·],Di∈C0(N,N),D0=D.则有以下定义:
定义5[5]如果对任意的x1,…x2n-1∈N,([·,…,·]t,Dt)满足以下条件:
(7)
(8)
则称([·,…,·]t,Dt)是n-李导子对(N,D)的一个单参数形式形变.
展开式(7)、式(8),并比较tk次项系数,发现式(7)、式(8)等价于以下两组等式对任意的k≥0均成立:
(9)
(10)
命题1[5]设([·,…,·]t,Dt)是n-李导子对(N,D)的一个形式形变,称([·,…,·]1,D1)为形式形变([·,…,·]t,Dt)的无穷小形变,则([·,…,·]1,D1)是复形C2(N,D)的一个2-上边缘.
定义6设([·,…,·]t,Dt)和([·,…,·]′t,D′t)是n-李导子对(N,D)的两个形式形变,则从形式形变([·,…,·]′t,D′t)到形式形变([·,…,·]t,Dt)的一个形式自同构定义为Φt=∑i≥0φiti:N[[t]]→N[[t]],其中φi∈C0(N,N),且φ0=Id,并满足以下条件:
Φt([x1,…,xn]′t)=[Φt(x1),…,Φt(xn)]t,
(11)
Φt∘D′t=Dt∘Φt.
(12)
如果存在一个形式自同构Φt:([·,…,·]′t,D′t)→([·,…,·]t,Dt),两个形式形变([·,…,·]t,Dt)和([·,…,·]′t,D′t)称为等价的.
定理2设([·,…,·]t,Dt)和([·,…,·]′t,D′t)是n-李导子对(N,D)的两个等价的形式形变,则它们的无穷小形([·,…,·]1,D1)和([·,…,·]′1,D′1)属于同一个上同调类.
证明设Φt:([·,…,·]′t,D′t)→([·,…,·]t,Dt)为一个形式自同构,比较等式(11)、式(12)的t次项系数,则有:
D′1(x)+(φ1∘D)(x)=D1(x)+(D∘φ1)(x),
即
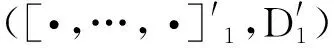
定理3n-李导子对(N,D)的一个形式形变称为平凡的,如果它等价于([·,…,·],D).若H2(N,D)=0,则n-李导子对(N,D)的任何形式形变均是平凡的.
证明设([·,…,·]t,Dt)是(N,D)的一个形式形变.从命题1可知,它的无穷小形变([·,…,·]1,D1)∈Z2(N,D).由于H2(N,D)=0,故存在φ1∈C1(N,N),使得([·,…,·]1,D1)=∂(φ1),定义Φt=Id-φ1t,则可得到形式形变([·,…,·]′t,D′t).其定义如下:
故([·,…,·]′t,D′t)等价于([·,…,·]t,Dt).将以上两个等式展开,有:
D′t=Id+D′2t2+D′3t3+….
经命题1中类似的计算,可得([·,…,·]′2,D′2)∈Z2(N,D).重复以上运算步骤,即可证明([·,…,·]t,Dt)等价于([·,…,·],D).
3 近似形变的延拓
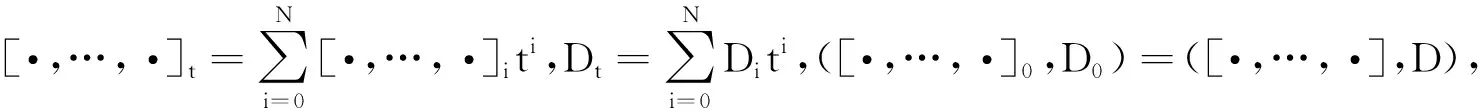
定义8设([·,…,·]t,Dt)是(N,D)的一个N阶形式形变,称([·,…,·]t,Dt)是可延拓的.若存在([·,…,·]N+1,DN+1)∈C2(N,D),使得在如下定义下:
[·,…,·]′t=[·,…,·]t+[·,…,·]N+1tN+1,D′t=Dt+DN+1tN+1,
([·,…,·]′t,D′t)是(N,D)的N+1阶形式形变.
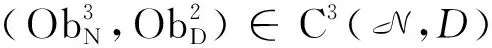
(13)
(14)
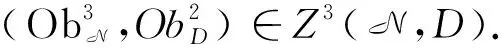

证明若(N,D)的N阶形变([·,…,·]t,Dt)是可延拓的,存在([·,…,·]N+1,DN+1)∈C2(N,D),使得([·,…,·]′t,D′t)在以下定义下:
[·,…,·]′t=[·,…,·]t+[·,…,·]N+1tN+1,D′t=Dt+DN+1tN+1,
([·,…,·]′t,D′t)是(N,D)的N+1阶形变,且对任意的k=N+1都满足式(9)、式(10).比较其中tN+1次的系数,可得:
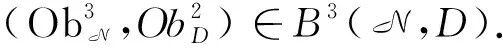
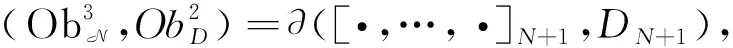
根据定理4和命题2,可以得到以下推论:
推论若H3(N,D)=0,则(N,D)的任何一个N阶形式形变均可延拓成(N,D)的形式形变.
4 命题2的证明
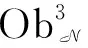
(15)
(16)
(17)
(18)
由等式(4)中d的定义,有:
(19)
(20)
(21)
(22)
(23)
(24)
(25)
(26)
(27)
(28)
(29)
(30)
(31)
(32)
(33)
由于对任意的0≤k≤N,([·,…,·]t,Dt)满足式(9),则有:

将式(25)展开得:
经计算可得:
(15)+(16)+(19)+(22)+(25)=
(34)
(35)
由于对任意的0≤k≤N,([·,…,·]t,Dt)满足式(10),因此展开式(34)和式(35)得:
同理,由式(10),对任意的0≤k≤N,有:
用它将式(26)、式(20)和式(23)展开,通过计算,可得:
(18)+(26)+(28)+(35)=
(36)
(37)
(17)+(20)+(23)+(30)+(32)+(34)=
(38)
(39)
继续计算可得:
(27)+(29)+(36)+(37)=
(40)
(21)+(24)+(31)+(33)+(38)+(39)=
(41)
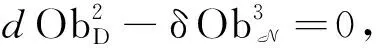
证毕.
5 实 例
设A是一个线性空间,e1、e2、e3为A的一组基,定义A上的括号运算[·,…,·]为[e1,e2,e3]=e1,则(A,[·,…,·])是一个3-李代数.
分别定义导子D:A→A和导子D′:A→A为:
D(e1)=e1,D(e2)=0,D(e3)=0,
D′(e1)=0,D′(e2)=0,D′(e3)=e1.
已知C0(A,A)=Hom(A,A)由基(gij)i,j=1,2,3生成,其中(gij)i,j=1,2,3定义为:
类似可得C1(A,A)由基(fi)i=1,2,3生成,(fi)i=1,2,3定义为fi(e1,e2,e3)=ei.
所以,C1(A,D)=C1(A,D′)=C0(A,A)是9维线性空间,C2(A,D)=C2(A,D′)=C1(A,A)×C0(A,A)是12维线性空间.经计算得:
(Ⅰ) dimZ1(A,D)=4且Z1(A,D)由基{g11,g23,g32,g22-g33}生成,故dimH1(A,D)=4.
(Ⅱ) dimZ2(A,D)=9,且以下列元素为一组基:
{(f1,0),(f2,g12),(f3,g13),(0,g11),(0,g21),(0,g23),(0,g31),(0,g32),(0,g22-g33)}.
(Ⅲ) dimB2(A,D)=5,B2(A,D)由基元{(f1,0),(f2,g12),(f3,g13),(0,g21),(0,g31)}生成,故dimH2(A,D)=4,基为{(0,g11),(0,g23),(0,g32),(0,g22-g33)}.
(Ⅳ)H1(A,D′)=Z1(A,D′)是4维线性空间,它的基为{g21,g31,g32,g33+g11-g22}.
(Ⅴ) dimZ2(A,D′)=9,由以下元素生成:
{(f1,0),(f2,0),(f3,g22),(f3,g33),(0,g11),(0,g21),(0,g23),(0,g31),(0,g32)}.
(Ⅵ) dimB2(A,D′)=5,由{(f1,0),(f2,g32),(f3,g33),(0,g31),(0,g21)}生成.故dimH2(A,D′)=4,且以{(f2,0),(f3,g22),(0,g11),(0,g23)}为基.
