部分信息下带跳线性二次平均场类型的二人零和微分对策问题
2022-05-30杨依芸唐矛宁孟庆欣
杨依芸,唐矛宁,孟庆欣
(1.浙江师范大学 数学与计算机科学学院,浙江 金华 321004;2.湖州师范学院 理学院,浙江 湖州 313000)
0 引 言
最优控制是在所有可能的控制方案中寻找最优方案,使控制系统能够最优地实现期望目标.在最优控制的基础上,当控制系统的状态方程为线性方程,且性能指标为二次时,最优控制可以以线性反馈的形式给出,这样的问题被称为线性二次(LQ)最优控制问题.在随机控制理论中,单个个体的状态不仅取决于其自身的状态,还取决于整个系统的平均值.这种被称为平均场模型(MF)的系统越来越受到学者们的关注.1956年,Kac首次考虑带平均场的随机微分方程(MF-SDE)[1].2013年,Yong研究了在有限时域内由布朗运动驱动的确定性系数的MF-SDE最优控制问题[2].2017年,Sun探讨了MF-LQ最优控制问题的开环可解性与性能指标(一致)凸性之间的关系[3].
在处理金融问题中的意外情况时,有必要用带跳系统来刻画.因此,对带跳线性二次最优控制问题的研究也是非常重要的.Boel等首次讨论了带跳过程的最优控制问题[4].2019年,Tang等探索了由布朗运动和泊松随机鞅测度共同驱动的MF-SDE的LQ最优控制问题[5],利用经典的凸变分原理[6]证明了最优控制的存在唯一性,并推导出两个Riccati方程,同时证明了最优控制具有状态反馈表示.最近一些学者还研究了与一般Lévy过程相关的Teugel鞅驱动的线性二次最优控制问题,获得了最优控制相应的对偶表示和状态反馈表示[7]。
由于我们观察到的信息并非总是完整的,这使得对MF-LQ问题在部分信息下的研究变得愈发深入,这类问题通常与滤波理论有关.2008年,Xiong系统地介绍了随机滤波理论[8].2016年,Ma等研究了在部分观测下MF-FBSDE的LQ最优控制问题[9].
对比最优控制问题,微分对策理论是研究当两个或多个决策人的控制作用同时施加于一个由微分方程描述的运动系统时,其各自实现最优目标对策过程的理论.该问题的研究可追溯到1965年Ho等的工作[10].1979年,Bernhard从闭环角度研究了DG问题[11].2020年,Moon研究了带有仿射项和随机系数的零和微分对策问题,并构建一个直接方法——配方法,以刻画精确的(反馈)纳什均衡,从而得到最优对策值[12].之后,Moon等对带跳的不定线性二次平均场类型的随机零和微分对策问题(I-LQ-MF-SZSDG-JD)的反馈纳什均衡进行了精确刻画[13].2021年,Sun讨论了带有确定性系数的二人零和随机线性二次微分对策问题,研究其开环鞍点与开环上下值函数的关系,并推导出开环上下值有限性的必要条件和开环鞍点存在性的充分条件[14].
本文主要讨论在部分信息下带跳线性二次平均场类型的二人零和微分对策(MF-LQSDG)问题.其创新有:①状态方程包含仿射项,是一个由二维布朗运动和泊松随机鞅测度共同驱动的随机微分方程;②状态方程和性能指标中不仅含有状态X(·)和控制u1(·),u2(·),还包含它们的期望,即所谓的平均场类型的微分对策问题;③在部分信息下,状态X(·)是Ft-适应的,控制u1(·),u2(·)是Gt-可测的,其中Gt⊆Ft.
1 符号与问题提出
1.1 符号
假设T是一个给定的正实数,(Ω,F,{Ft}0≤t≤T,P)是一个完备概率空间,定义W(t)={W1(t),W2(t)}0≤t≤T是一个标准的二维布朗运动.记P为[0,T]×Ω上的Ft-可料的σ-代数,B(Λ)为任何拓扑空间Λ的Borelσ-代数.设(,B(),ν)是满足ν(E)<∞,∀E∈B()的可测空间,η:Ω×Dη→是具有特征测度ν的Ft-适应的平稳泊松点过程,其中Dη是(0,∞)的可数子集.那么由η诱导的计数测度为:
μ((0,t]×A)#{s∈Dη;s≤t,η(s)∈A},对t>0,A∈B(),
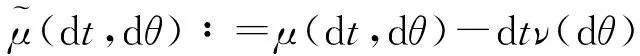
在现实的很多情形中,控制u(·)只能在部分信息下观测.在这种情况下的可允许控制过程u(·)是Gt-可料过程,满足Gt⊆Ft.记G={Gt}0≤t≤T表示t时刻控制者的有效信息.假设Gt=Ft-δ,其中δ>0是一个固定的信息延迟.
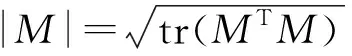
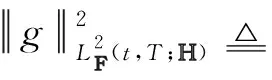

Lν,2(;H)为全体H-值可测函数r:→H构成的空间,且满足:
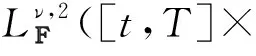

1.2 问题的提出
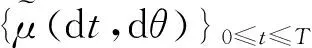
(1)

其中,ui(·)∈Ai是[t,T]内决策者i在部分信息下的可允许开环控制过程;A1×A2称为决策者的可允许开环控制集;系统(1)的强解记作X(·)或X(x,u1,u2)(·),称为在初始时刻t以x为初始状态的状态过程;(X(·),u1(·),u2(·))称为可允许控制三元组.
性能指标定义为如下形式的二次泛函:
J(t,x;u1(·),u2(·))=[X(T)],[X(T)]〉]+[u1(s)],[u1(s)]〉+[u2(s)],
(2)

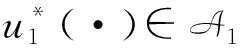
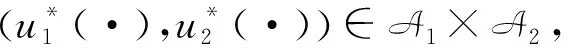
(3)
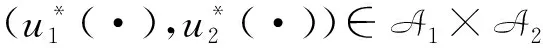
为下文符号的简便,记m=m1+m2,定义
自然地,A=A1×A2.基于以上符号,状态方程(1)可改写为:
(4)
性能指标(2)可改写为:
J(t,x;u(·))=[X(T)],[X(T)]〉]+[u(s)],
(5)
下面介绍本文所需的基本假设:



假设3设t∈[0,T],存在常数δ>0,其满足:
2 开环鞍点与最优对策值
在给出本文的重要结果前,首先引入两个Riccati方程:
(6)
(7)
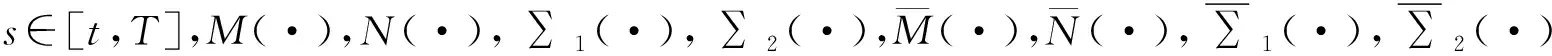
(8)
其次给出以下BSDE:
(9)
以及常微分方程:
(10)
本文的主要结果:
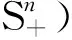
u*(s)=-[N(s)-1M(s){(X*(s)-[X*(s)])|Gs}+N(s)-1{∑1(s)|Gs}+{∑2(s)|Gs}],
(11)
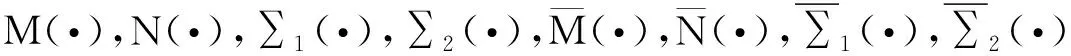
(12)
相应的对策值函数表示为:
V(t,x)=〈Π(t)x+2η2(t),x〉+[〈P(s)σ1(s)+ξ1(s),σ1(s)〉+〈P(s)σ2(s)+〈P(s)h(s,θ)+ζ(s,θ),h(s,θ)〉ν(dθ)+2〈η1(s),b(s)-[b(s)]〉+ 2〈η2(s),
(13)

(14)
不难得到:
下面令
J(t,x;u(·))=[X(T)],[X(s)],[X(s)]〉+[u(s)],
(15)

J1(t,x;u(·))=[X(s)],[X(s)]〉+[X(s)],[u(s)]〉+[u(s)],[u(s)]〉+ 2[σ1(s)]+[σ2(s)]+[ξ2(s)]}+[h(s,θ)]+[ζ(s,θ)]}ν(dθ),[X(s)]〉+[σ1(s)]+[σ2(s)]+[ξ2(s)]}+[h(s,θ)]+[ζ(s,θ)]}ν(dθ),[u(s)]〉+〈P(s)h(s,θ),h(s,θ)〉ν(dθ)+〈ζ(s,θ),h(s,θ)〉ν(dθ)+2〈η1(s),b(s)-
(16)
类似地,对〈Π(s)[X(s)]+2η2(s),[X(s)]〉,应用公式得:
J2(t,x;u(·))=〈Π(t)x+2η2(t),x〉+[X(s)],[X(s)]〉+[u(s)],[u(s)],[u(s)]〉+[b(s)],[X(s)]〉+[u(s)]〉+2〈η2(s),
(17)
综合式(15)至式(17)有:
J(t,x;u(·))=〈Π(t)x+2η2(t),x〉+〈P(s)σ1(s)+ξ1(s),σ1(s)〉+〈P(s)σ2(s)+ξ2(s),σ2(s)〉+〈P(s)h(s,θ)+ζ(s,θ),h(s,θ)〉ν(dθ)+2〈η1(s),b(s)-[b(s)]〉+ 2〈η2(s),
(18)
当控制u(·)满足

(19)
时,对策值函数
J(t,x;u(·))=〈Π(t)x+2η2(t),x〉+〈P(s)h(s,θ)+ζ(s,θ),h(s,θ)〉ν(dθ)+ 2〈η1(s),b(s)-[b(s)]〉+2〈η2(s),[b(s)]〉-
(20)
在部分信息下,u(·)是Gt-可测的,只需对式(19)利用条件数学期望[·|G]的性质,即可得到式(11),则相应的最优对策值函数满足式(13).
当b(·),σ1(·),σ2(·),h(·,·)=0时,记对应的最优对策值函数为V0(t,x):
V0(t,x)=〈Π(t)x,x〉.
3 特 例
第2节得到了开环鞍点u(·)的状态反馈表示,但{(X(s)-[X(s)])|Gs}的形式仍是未知的.为写出滤波方程,给出以下特例:

(21)

特殊地,假设Gt=σ{W2(t),0≤t≤T},则控制u1(·),u2(·)是Gt-适应的.假设观测方程为:
y(s)=W2(s),
为得到最优控制更精确的表达,可以利用滤波理论.假设
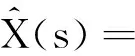
根据文献[8]的引理5.4,有下面的命题:

(22)
且得到开环鞍点的反馈表示:
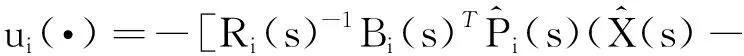
(23)
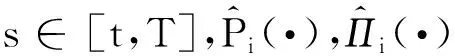
(24)
(25)

(26)
以及常微分方程:
(27)
4 结 语
本文主要研究了部分信息下带跳MF-LQSDG问题,利用配方法得到了开环鞍点的反馈表示,且将MF-LQ问题看作MF-LQSDG问题的一个特殊情况.本文研究的系数是确定性的,时间区间是有限的,对随机系数和无限时区的研究可为后续的学习提供方向.
