面向航天器结构健康状态监测的数据压缩感知算法研究

李 钰 李 晨† 王常龙 梅占东 张世一

(1. 上海卫星装备研究所，上海 200240; 2. 上海空间环境模拟与验证工程技术研究中心，上海 200240;3. 西安电子科技大学电子信息攻防对抗与仿真技术教育部重点实验室，西安 710071;4. 西安交通大学数学与统计学院，西安 710049)

0 引言

航天器产品具有小子样、长寿命、高可靠性和基本不可维修等特点，并且在发射、在轨、运行过程中需要经历复杂的环境剖面。随着智能化结构技术的不断发展，在航天器产品发射、在轨运行过程中对温度、加速度、应变、形变等参数进行实时监测需求逐渐增多，航天器产品结构健康状态监测逐渐成为研究热点。一方面通过光纤传感技术和无线传感网络技术实现对结构健康状态监测数据的实时采集获取，目前国内外已在多个航天器上取得了技术应用，而另一方面如何实现对长时间和多个传感器监测到的大量数据高效传输和存储也是亟需关注的方向。通过采用数据压缩算法可在保证压缩精度的情况下获得较高的压缩比，减少数据的储存和传输量，并且缩短数据处理时间，最终在较小失真的情况下使用很少的监测数据描述航天器产品结构运行状态。Ganesan 等人[1]在基于振动的结构故障诊断中应用压缩感知技术对振动信号进行监测与诊断，以减小数据的存储量；北京卫星环境工程研究所田引黎等人[2]提出了基于半张量积压缩感知的形变数据重构方法，采用该方法对形变信号进行随机采样，实现较高精度的重构；南京邮电大学宋春晓[3]利用压缩感知在Lamb 波结构健康监测中的开展了应用研究。本文将稀疏恢复技术应用于航天器结构健康状态监测数据传输问题中，对于大量监测数据将其分段处理，每一段分别通过压缩测量，在数据接受端通过稀疏恢复算法进行恢复，最后通过卫星振动试验数据验证该方法的有效性。该方案实现了利用低维数据传输高维数据的效果，为解决航天器结构健康状态监测过程中数据高效传输提供理论支持。

1 压缩感知原理与建模

在实际应用中，我们需要处理和监测的数据信号普遍是高维度或高频率的，而采集这些大量的数据对于整个系统的信息存储、传输、编译等环节都提出了极高的要求。为了克服这一困难，由Donoho 等人[4–7]建立了压缩感知理论体系，实现了用较低采样频率的方式恢复高维信号的技术突破，而这些工作也为稀疏信息恢复的理论[8]工作奠定了重要的基础支撑。

稀疏表示、测量矩阵和重构算法是压缩感知基本模型的三要素，稀疏表示是压缩感知理论的重要前提，在实际应用中，大部分信号在小波基上展开后，其小波系数向量的稀疏性表现为大部分元素为0 或是较小的值，只在部分位置上有着较大的数值。从数学角度讲，当一个向量中的大部分位置的元素为零或是较小值时，我们称该向量是稀疏的[4]。特别地，若//x//0≤k，我们也称向量x是k稀疏的，其中

测量矩阵的设计也是压缩感知应用的重要条件，其对于信号重构具有重要意义，RIP 条件[4]已被证明是测量矩阵所要满足的充分条件，Donoho 给出了满足此条件的测量矩阵的三个特征：

1) 列向量满足一定的线性独立性；

2) 测量矩阵的列向量具有某种类似噪声的独立随机性；

3) 满足稀疏度的解是满足1 范数最小的向量。

重构算法是完成从观测信号到目标信号的恢复过程，是压缩感知的关键内容，同时也是研究中的重点和难点，对于稀疏向量的恢复，可以建模为以下l0最小化[9–10]问题，而该模型就是稀疏信息恢复理论中的本源优化问题

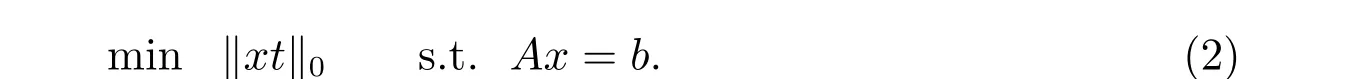
根据经典线性代数理论，欠定方程组Ax=b一般有无穷多个解，但是基于解的稀疏性假设前提，l0最小化问题寻求的是这些解中最稀疏的解。因此，稀疏的先验假设[11–12]是极为重要的。如果航天器结构健康状态监测数据在时域上不具备稀疏特性，可以通过变换域将其转换成稀疏信号，本文将稀疏恢复技术应用于航天器结构健康状态监测数据传输问题中，对于大量监测数据将其分段处理，每一段都通过压缩测量，在数据接收端通过本文设计的稀疏恢复算法进行恢复，从而达到利用低维数据传输高维数据的效果。

2 分式替代模型与算法理论分析

作为稀疏恢复中的本源模型，l0最小化模型已经被证明为一个NP-HARD 问题，因此直接求解该问题是很困难的。寻求直接求解该模型的研究工作方向之一是启发式算法设计，其中的代表是正交匹配追踪算法[5](OMP)以及基于其的改进算法。对于OMP 类型的贪婪算法[6]，其优点在于它是直接被设计用来求解l0最小化模型，而且算法复杂度低。但是这类方法缺点主要有以下几点。第一，此类算法受噪声影响水平较大。这是因为实际问题中的稀疏信号存在有一些较小值的分量，同时受到测量误差的影响，容易在支撑基更新的步骤出现误选，而对于OMP 算法，只要在迭代中支撑基更新出错，就会直接导致整个算法恢复失败。第二，成功恢复的条件较为苛刻。对比于其他算法，如OMP 以及其改进算法[13–14]，几乎都需要对真实解的稀疏度预估。并且该预估值还需要比较接近真实解。可是在许多实际问题中，真实解的稀疏度是难以判断的[15–16]。因此，本章将会给出一种新的替代函数与其对应的算法，通过对其局部最优解性质的讨论给出其收敛性证明。在本章及后面的篇幅中，我们定义函数

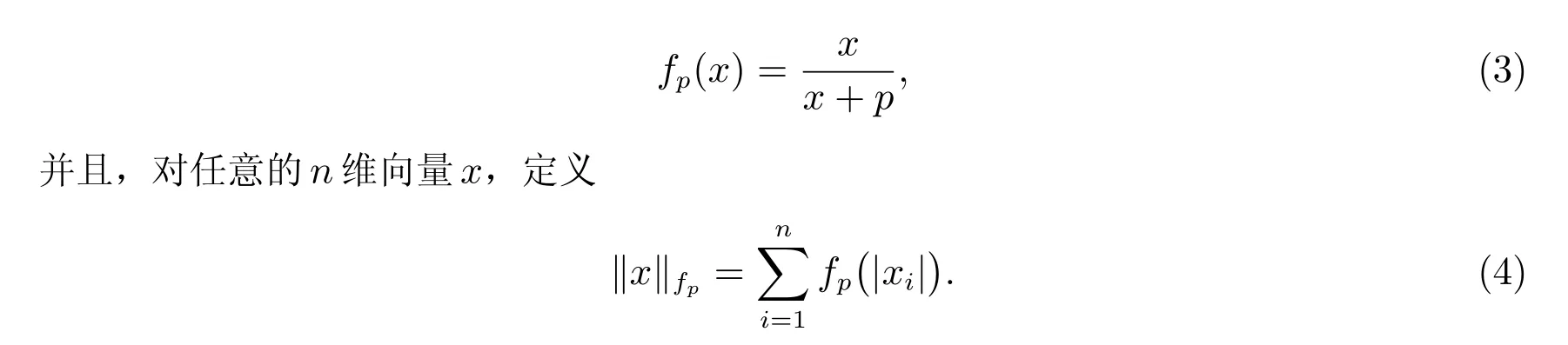
根据定义可以发现，随着参数o趋向于0，函数的性质与0 范数越来越接近。例如，在图1 中所示的二维情况，当p的取值趋向于0 时，函数的图像与0 范数图像越来越近。

图1 分式函数图像

因此，当参数p的取值足够小时，我们可以通过求解如下lfp模型用来恢复原问题中的稀疏向量随后给出这个模型的局部解性质以及根据这个性质所衍生出的不动点迭代算法。对于给定的n维向量x，定义n维对角矩阵

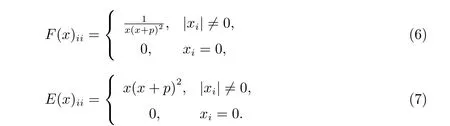
接下来，我们将通过以下定理展示lfp最小化模型的一个重要性质，根据这个性质我们可以得到一个不动点迭代算法。

定理1 如果x∗是lfp最小化模型(5)的解且每一个分量均不为0，测量矩阵是一个满秩矩阵，则有

证明 根据假设，因为x∗的每一分量不为0，因此在该点处足够小的领域内，优化函数可以视为一个可微函数，又因为测量矩阵是满秩矩阵，因此考虑其KKT 条件，定义拉格朗日对偶函数L(x,λ)为

在定理1 中，我们详细地讨论了模型的局部解性质，虽然原问题不能直接应用KKT 条件，但是通过一定数学变化得到了类似的结果。但是注意到，上述结果是建立在解的每一个分量不为0 的前提下，如果没有这个假设直接带来的影响就是AE(x∗)AT有可能不是可逆矩阵，为了解决这个问题，我们可以考虑求其伪逆代替原式结果。根据这个结论，很容易地得到以下不动点算法。

算法1 分式lfp 最小化模型算法Require: A ∈Rm×n, b ∈Rn, p,K Ensure: x∗x1 =arg minAx=b //x//1 E =E(x1)for k =1,2,··· 直到满足终止条件do xk+1 1 =FAT(AFAT)†b S ={i||xk+1 i |∈V a}E =E(xk+1)k =k+1 end for x∗=xk+1

下面给出这个算法的收敛性证明。

定理2 根据算法1 得到的序列{xk}满足

根据引理1 的结果，我们可以发现，分式模型的算法从本质上也是一种支撑基判断方法，但是与OMP 类型的方法不同，本文所提方法是从局部最优解性质入手，不需要稀疏先验知识，因此，在每一步迭代中，我们可以用过对当前解中过于小的分量使其值为0，加速其收敛速度，也通过选取最主要部分的支撑基应对含有噪声的情形。因此有以下改进算法。

算法2 改进的分式lfp最小化模型算法

Require: A ∈Rm×n, b ∈Rn, p,e,K Ensure: x∗x1 =arg minAx=b //x//1 E =E(x1)for k =1,2,··· 直到满足终止条件do xk+1 1 =FAT(AFAT)†b S ={i||xk+1 i |∈V a}S ={i:|xk+1 i |>e}xk+1 1 =arg minsupport(x)⊂S //Ax −b//22 E =E(xk+1)k =k+1

end for x∗=xk+1

3 基于卫星振动试验数据的算法验证

航天器结构在发射、在轨环境下会受振动、声、加速度、冲击等多种动力学环境作用。据美国宇航局统计[17]，卫星发射上天后第一天所出现的故障，有30%∼60%是由于动力学环境所引起的，因此对于监测航天器结构在振动环境下的响应数据是航天器结构健康状态监测的一个重要内容。通过航天器振动环境模拟试验可以再现航天器结构在发射飞行过程所经受的振动环境[18]，获得结构在振动响应。为验证本文提出的算法在后续航天器结构健康状态监测数据处理中应用的可行性，选取了某气象卫星整星地面振动试验过程中的加速度响应数据作为研究对象。试验中在卫星不同结构处布置了多个加速度测点，本文选取1 个加速度测点数据利用本文算法进行了处理和分析验证。

根据航天器的构造，一级液体火箭发动机通过箭体结构传递时，能量逐渐损失，尤其高频部分由于循环次数多，能量损失也多，传递到安装在整流罩内的卫星时，推力脉动只剩下很少的能量，一般400 Hz 以上的推力脉动就已经很弱。因此目前在整星振动试验中通常采样频率在400 Hz 以下，因此这里选取采样率为400 Hz，整个振动试验时长62.5 s，故有25 000 次结果。根据点的方向(分别为x、y、z三个方向)以及信噪比(SNR 为40 dB 和20 dB)分别得到的6 组不同的数据，在压缩比为0.4 的条件下，我们对每次数据直接进行处理恢复，其中某一次恢复实验(分别为点x方向，信噪比为40 dB 和点x方向，信噪比为20 dB)得到的结果以及与15∼25 s 放大结果如图2、图3 所示，图4 给出了每种算法的结果图，可以看出，作为经典匹配追踪算法如OMP 算法和CoSaMP 算法，二者在图像的外部轮廓上出现了较多的“毛刺”，原数据恢复效果不如本文算法结果。

图2 恢复信号时域图

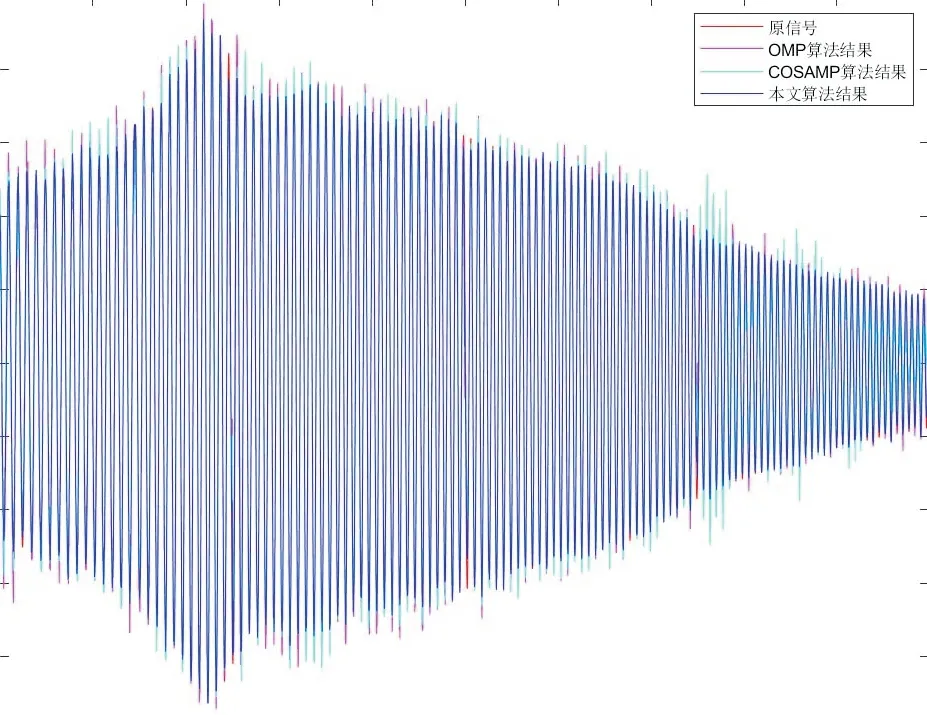
图3 15∼25 s 放大结果时域图

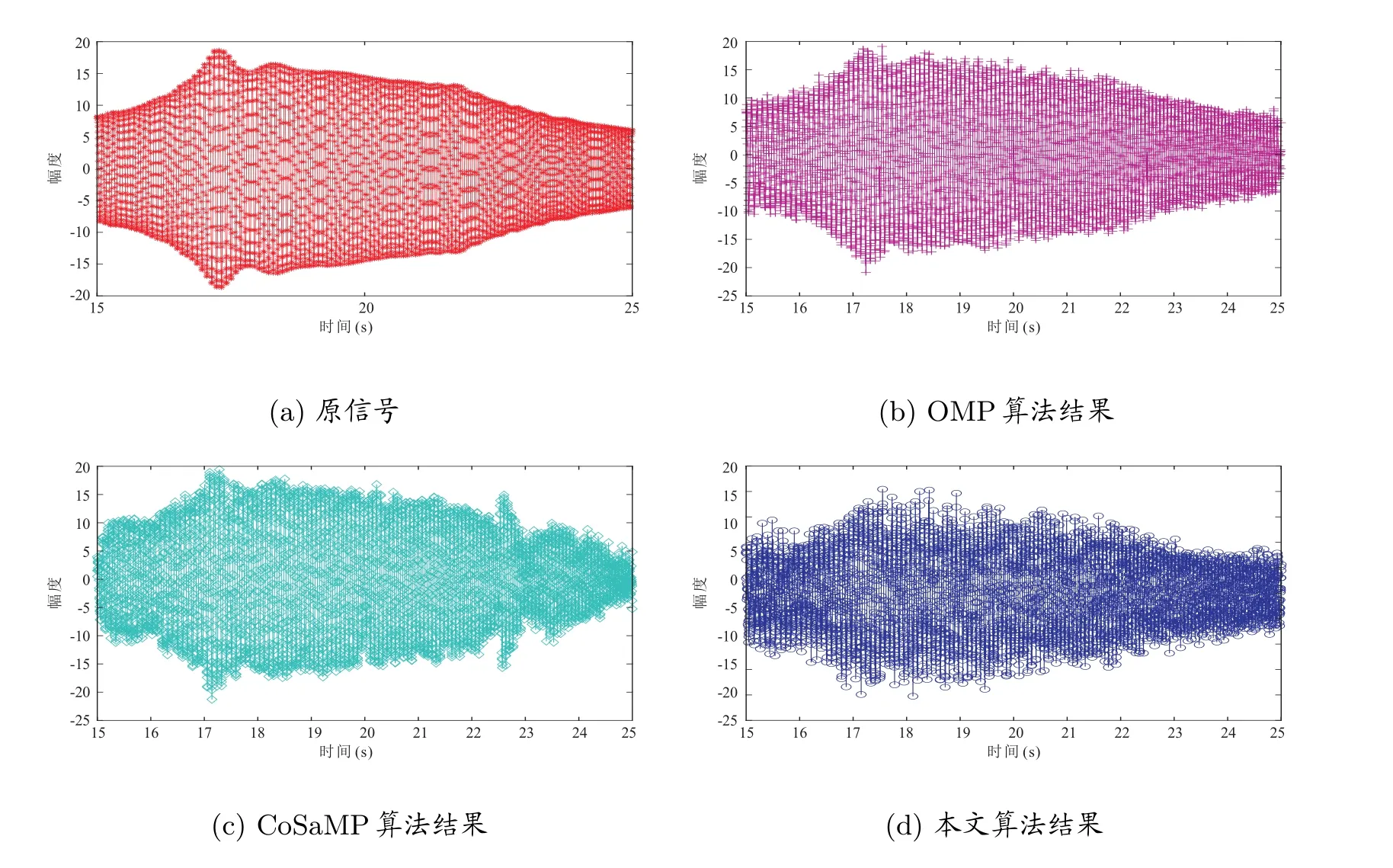
图4 原信号与各算法结果

经计算得到统计的恢复结果误差如表1 所示，每一小格中的三行数据从上至下依次为范数相对误差结果、范数相对误差结果、无穷范数相对误差结果，从表1 可以看出，最右边一列中的本文方法处理得到的各种相对误差均明显小于其他现有两种算法的处理结果。

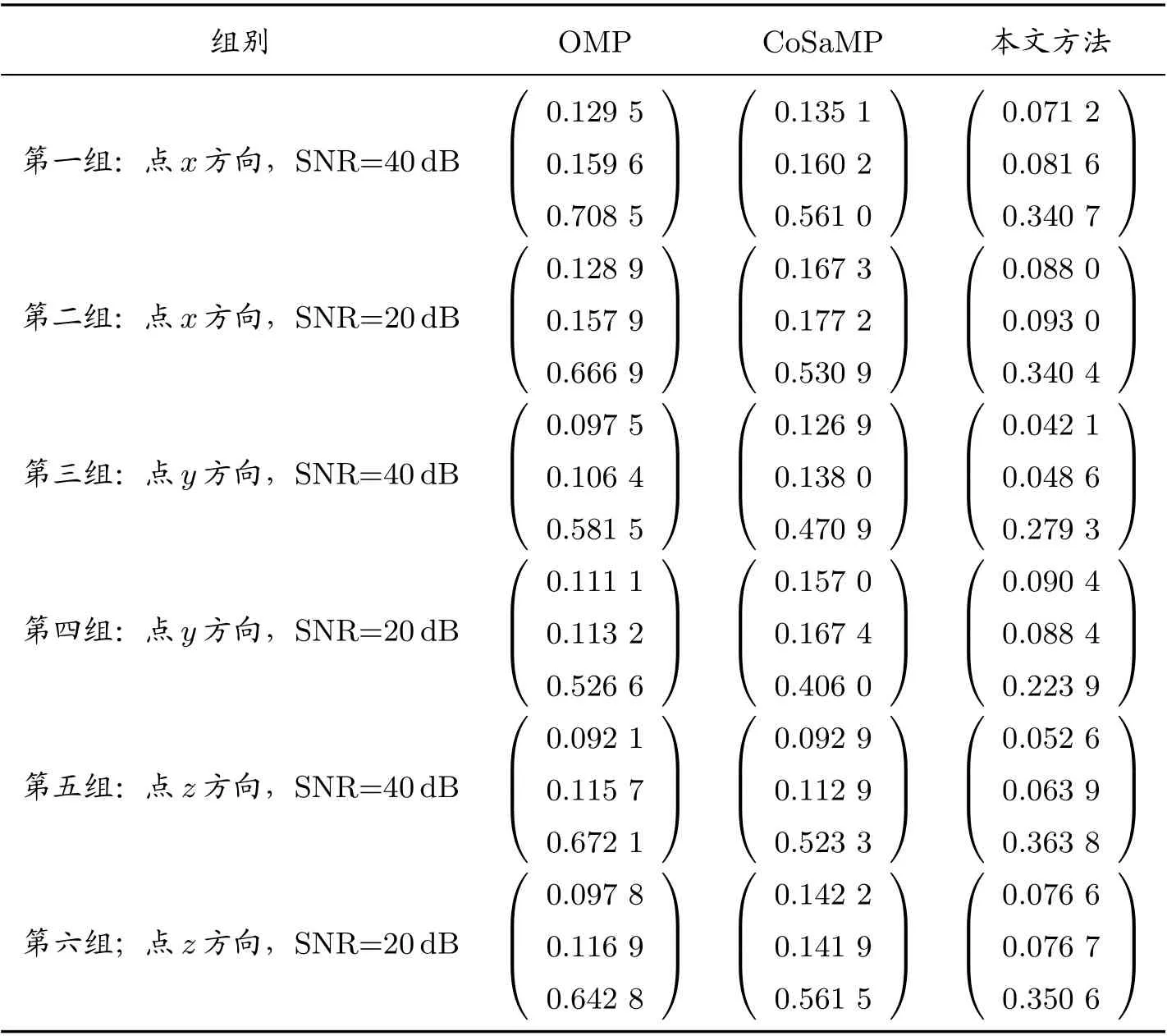
表1 相对误差总表

为了便于处理以及更加细致化地对结果进行分析，将每一次的实测数据分为25 组，每组有1 000 次数据，对每一组数据独立进行恢复处理。如图5、图6 为不同算法的部分恢复结果(时域)以及通过傅里叶变换到频域后的结果，不论是在时域还是频域，另外两种算法依然在图像上出现了一些凸出的“毛刺”，本文所提算法所得结果相比较能够较好地恢复出原信号。

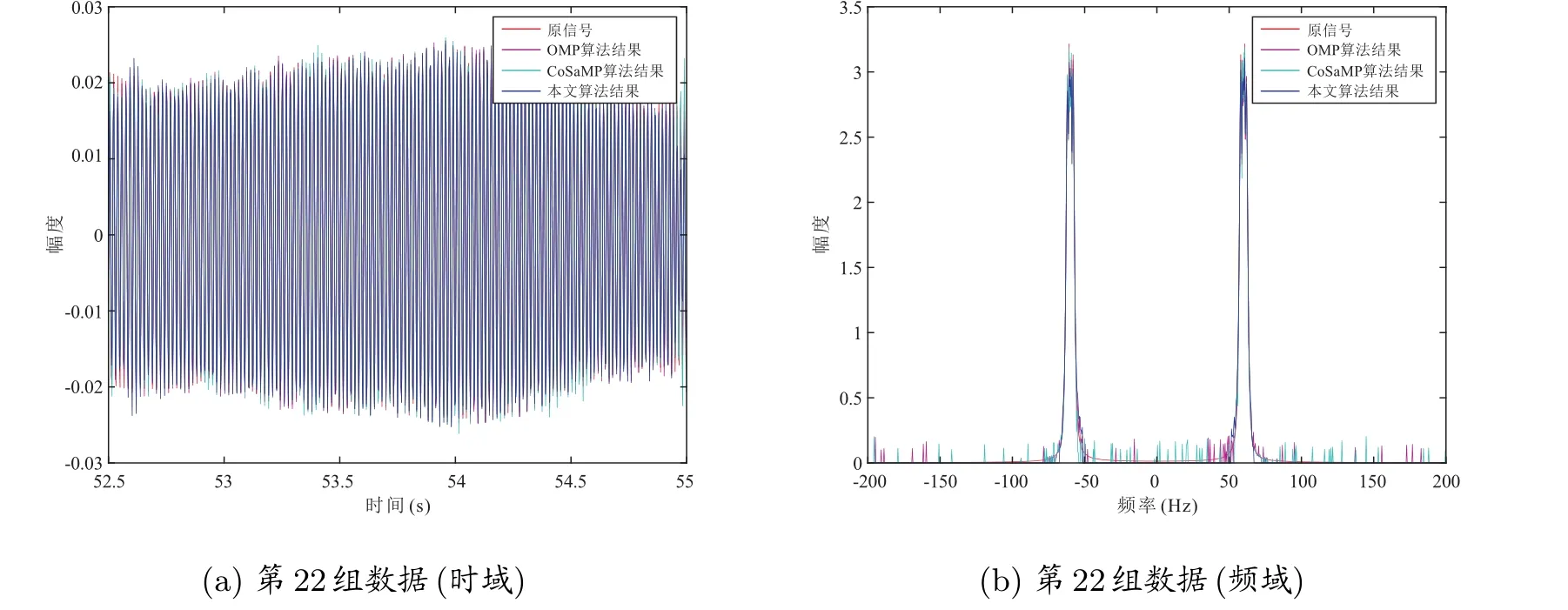
图5 点x 方向，信噪比40 dB 条件下结果

图6 点z 方向，信噪比20dB 条件下结果

将每组恢复处理得到的不同的相对误差结果绘制成折线图如图7 至图12 所示，每一行的左中右依次为范数相对误差结果、范数相对误差结果、无穷范数相对误差结果的图像，由多组图的结果可以看出，本文所提方法的相对误差结果(在图中为红线部分)在大多数组里都低于其他两种算法的结果，其恢复效果要好于其他两种算方法。

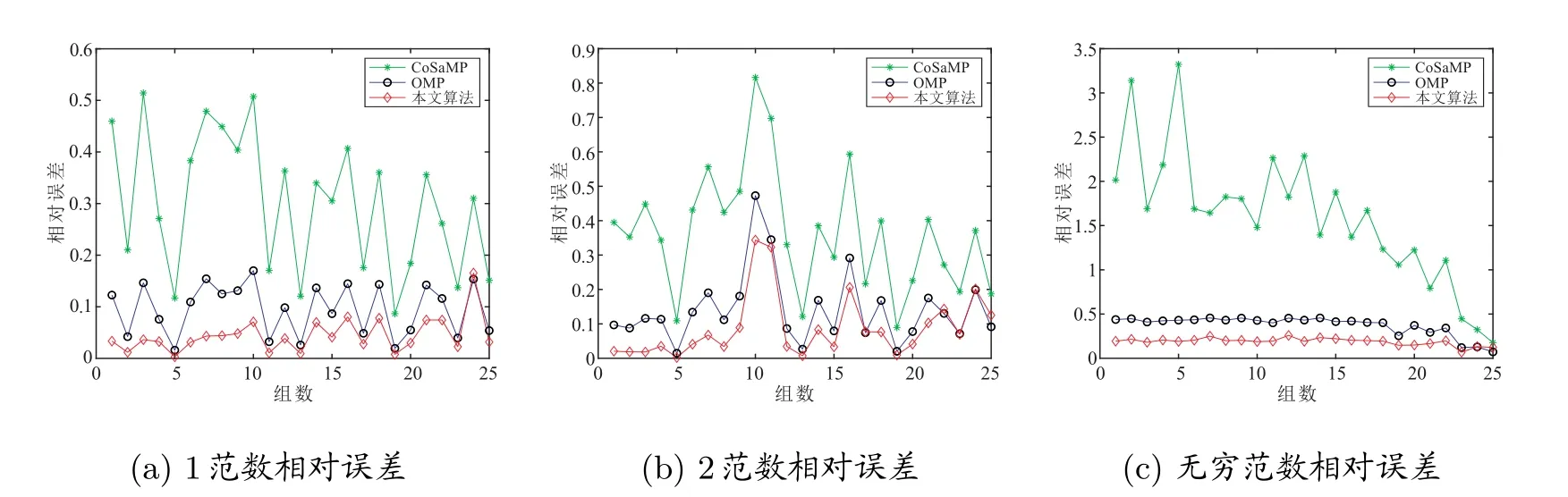
图7 第一组数据统计

图8 第二组数据统计

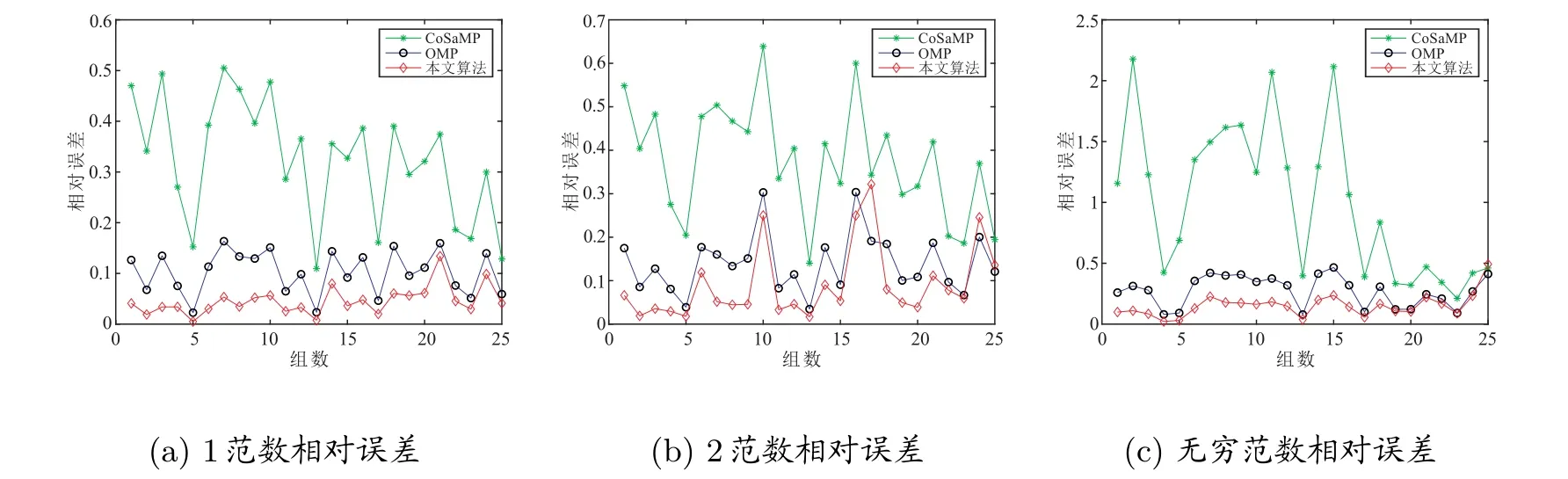
图12 第六组数据统计

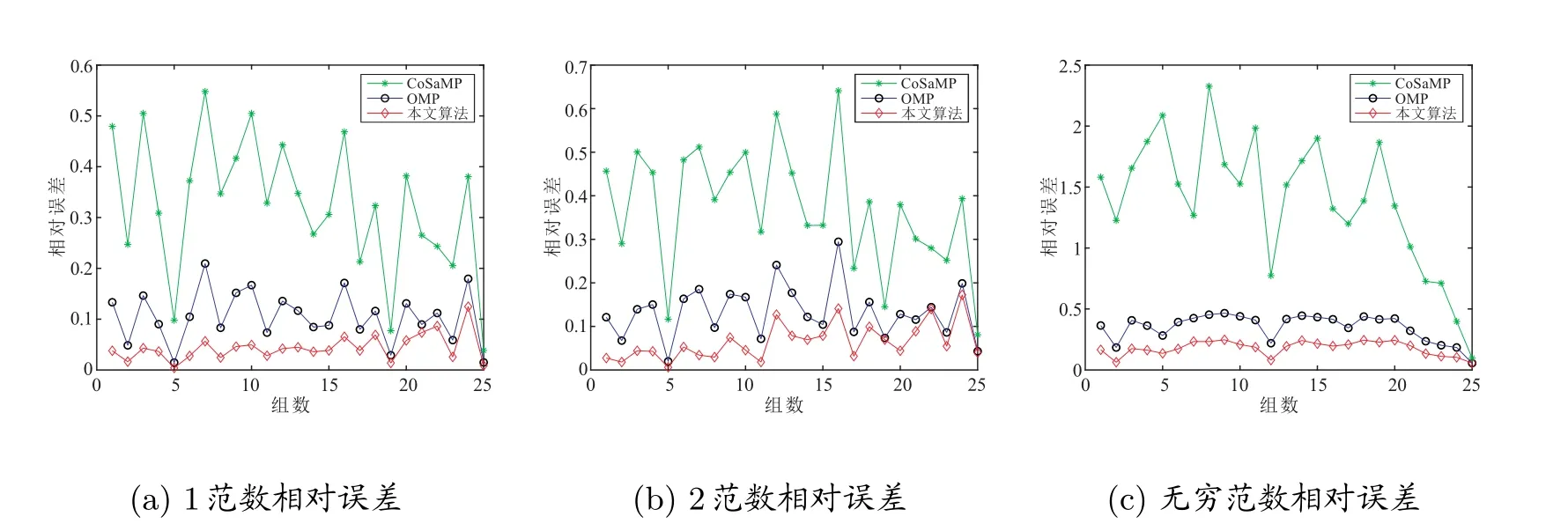
图9 第三组数据统计

图10 第四组数据统计

图11 第五组数据统计

4 结论与应用前景

本文将稀疏恢复技术应用于航天器结构健康状态监测数据传输问题中，并对所提算法进行卫星振动试验数据恢复验证，对比结果表明本文所提算法处理得到的数据恢复相对误差明显小于经典的匹配追踪算法，可以较为可靠的恢复出原数据信号，在较小失真的情况下使用很少的数据描述试验的全过程，具有其一定的优越性。后续将进一步结合航天器结构变形、振动、应变等多种动态响应数据信号处理开展应用验证，为解决未来航天器结构健康状态监测的关键技术提供支持。