求解带有不连续波数的二维变系数Helmholtz 方程的一种高精度紧致差分方法
2022-05-30冯秀芳
王 芳, 冯秀芳
(宁夏大学数学统计学院,银川 750021)
0 引言
Helmholtz 方程是一类描述时谐波、航空声学、水下声学以及电磁波散射等现象的物理模型。求解该方程常用的数值方法有有限元方法[1]、边界元方法[2]、有限差分方法[3–7]等。由于Helmholtz 方程本身的复杂性,研究其数值计算比较困难,特别是对于变系数、变波数和大波数问题仍需深入研究。因此,研究Helmholtz 方程的数值计算方法具有重要意义。
近年来,国内外许多学者采用有限差分方法在求解Helmholtz 方程方面做了大量的研究。1995 年,Harari 和Turkel[3]建立了均匀网格下的四阶格式和非均匀网格下的三阶格式;1998 年,Singer 和Turkel[4]构造了两种具有四阶精度的格式,一种格式是基于pad´e 近似的推广,另一种格式是基于Helmholtz 方程本身,计算高阶导数对其进行修正;2007 年,Nabavi 等人[5]基于方程本身对高阶导数近似,构造了一种新的六阶九点紧致差分格式。以上工作研究的都是波数为常数的情况。2011 年,Wong 和Li[6]提出了任意波数的Helmholtz 方程的有限差分格式;2013 年,Turkel 等人[7]构造了二维和三维变波数Helmholtz 方程的六阶紧致差分格式;Feng 等人[8–10]利用浸入界面方法,构造了常系数下带有不连续波数的Helmholtz 方程的三阶、四阶紧致差分格式。
本文针对带有不连续波数的二维变系数Helmholtz 方程构造了四阶紧致差分格式。首先,介绍了二维变系数Helmholtz 方程的四阶紧致差分格式[11–12]。其次,研究波数k是分段常数的界面问题,界面问题生活中随处可见,例如不同的两种物质:水和油;或者相同的物质,但处于不同的状态:水和冰。浸入界面方法[13–14]是一种处理界面问题的方法,该方法适用于求解区域是笛卡尔坐标系、极坐标系或球面坐标系下的均匀网格、自适应网格或者三角剖分,在远离界面的地方使用标准的有限差分方法或者有限元方法;经过界面时,根据界面关系对有限元或者有限差分格式进行局部修改,使其在整个求解区域内达到高精度。本文选取在网格线上的垂直界面,在文献[12]的基础上构造了一种新的四阶九点差分格式,该格式在界面处可以达到四阶精度。最后,通过数值实验验证了该格式的有效性和可行性。
1 四阶紧致差分格式的建立
考虑下列二维变系数Helmholtz 方程

其中各系数为
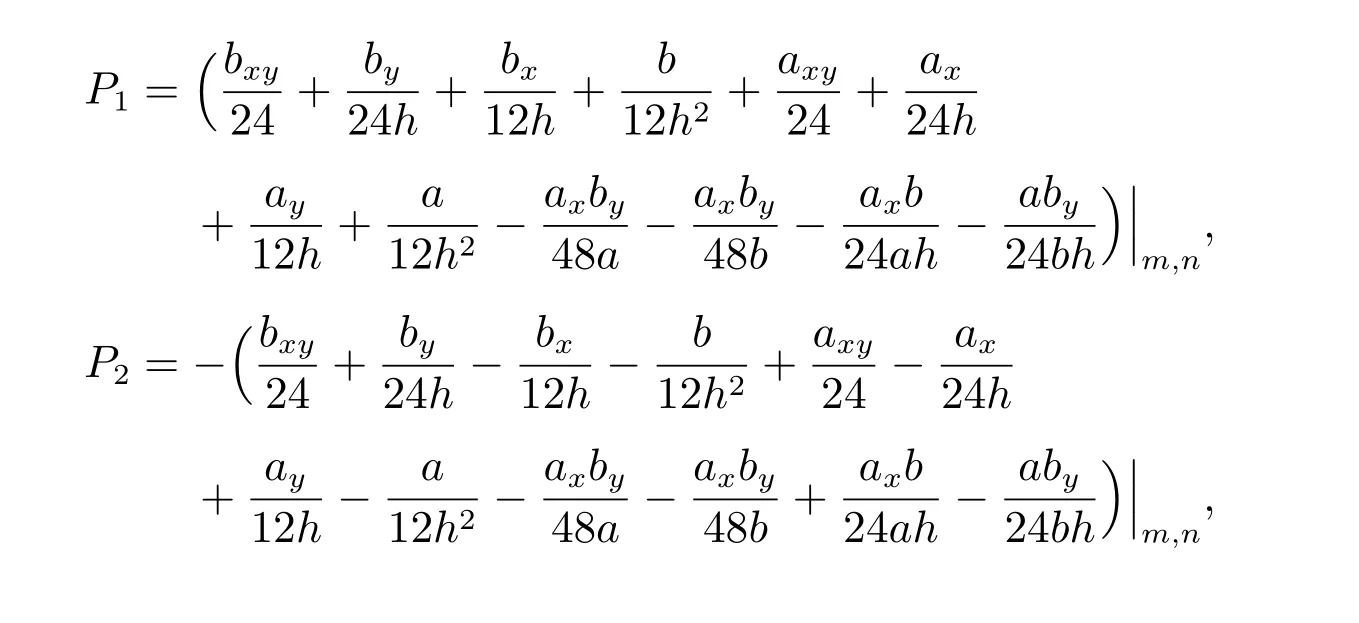

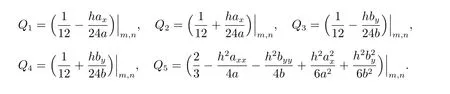
2 波数k(x,y)为分段常数的四阶紧致差分格式
考虑(1)式中的波数k(x,y)为分段常数的二维变系数Helmholtz 方程,即
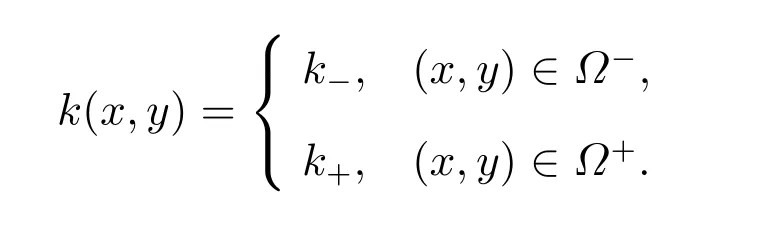
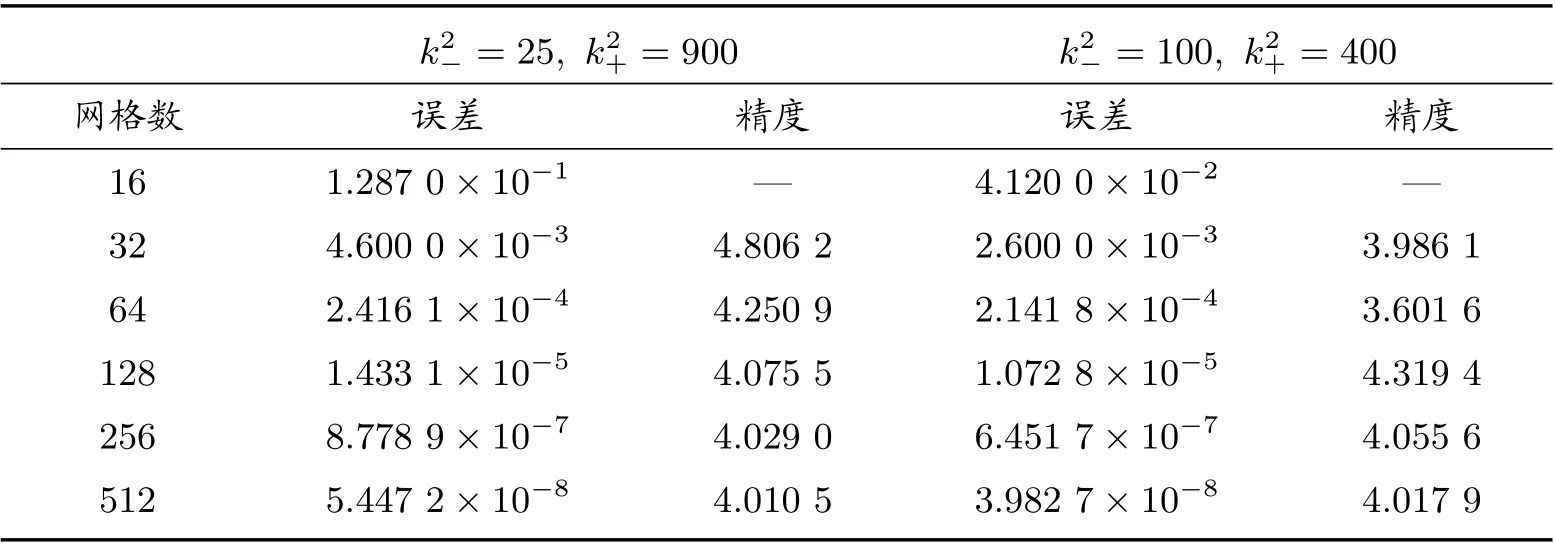
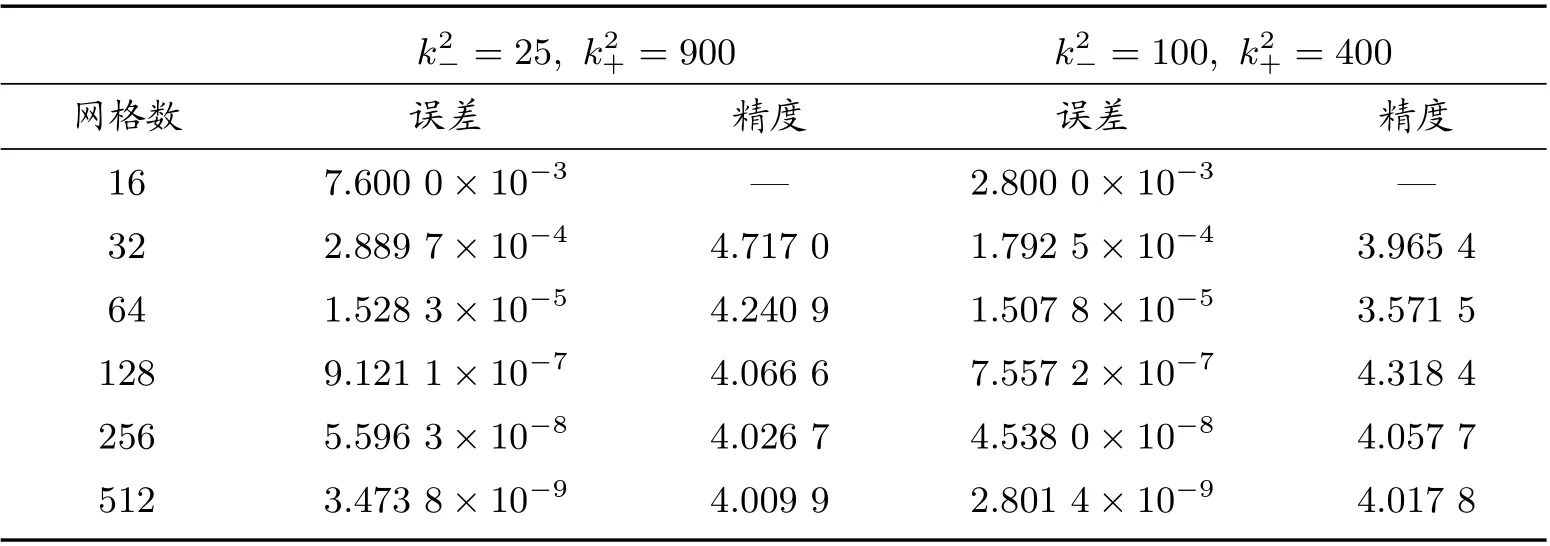
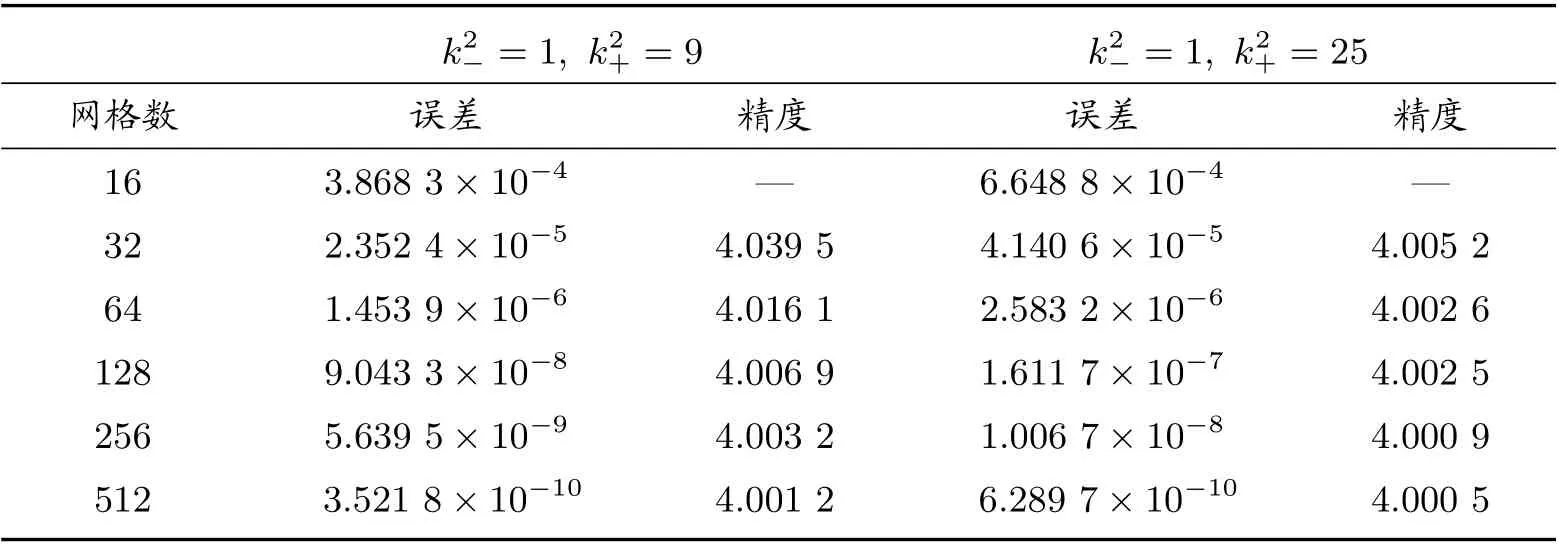
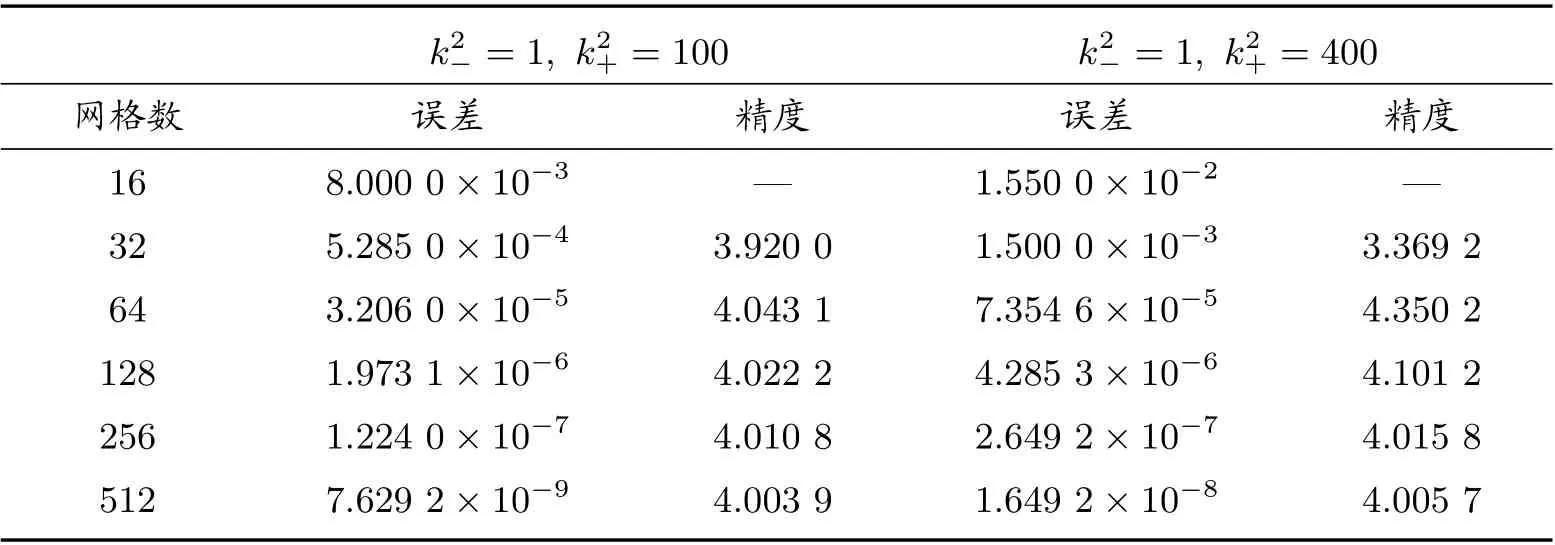
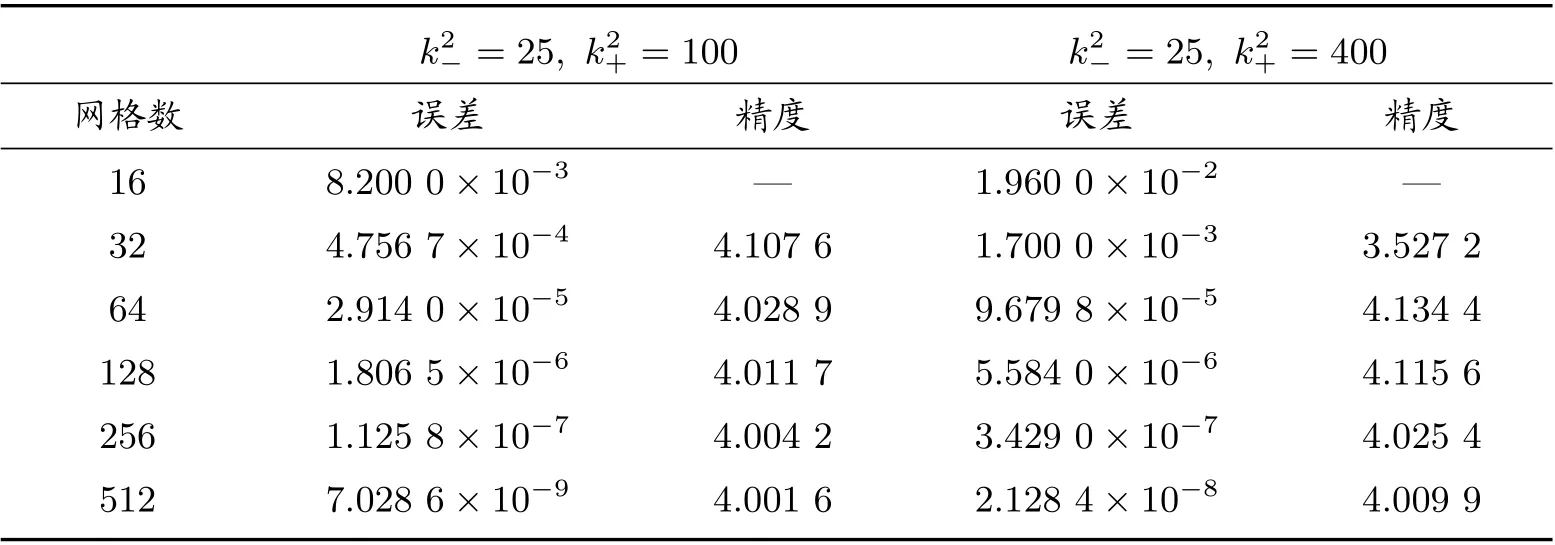
矩形区域Ω被划分为Ω−, Ω+两个区域,即Ω−={(x,y)|e 图1 k 为分段常数时,求解区域示意图 若格式中网格节点全部在界面的一侧时,如图1 中A、C 部分所示,则使用格式(2)进行求解;若格式中网格节点涉及界面区域两侧时,如图1 中B 部分所示,根据浸入界面方法和有限差分方法可推导界面处四阶紧致差分格式。 方程在界面x=α上满足跳跃条件 引理1 假设(1)式的k(x,y)为分段常数,则f(x,y)也是分段的,可以得到如下跳跃条件 将(13)式代入(6)式,并整理得到界面处的四阶紧致差分格式 为了验证本文构造的四阶紧致差分格式(14)式的精确性和有效性,考虑以下两个具有精确解的问题,均采用Dirichlet 边界条件,其中精度 表1 当[k2]=8 与[k2]=24 时,差分格式的误差与精度 表2 当[k2]=99 与[k2]=399 时,差分格式的误差与精度 表3 当[k2]=75 与[k2]=375 时,差分格式的误差与精度 表4 当[k2]=875 与[k2]=300 时,差分格式的误差与精度 表5 当k2−=1, k2+ =9 与k2+ =25 时,差分格式的误差与精度 表6 当k2−=1, k2+ =100 与k2+ =400 时,差分格式的误差与精度 表7 当k2−=25, k2+ =100 与k2+ =400 时,差分格式的误差与精度 本文利用有限差分方法和浸入界面方法构造了带有不连续波数的二维变系数Helmholtz 方程的四阶紧致差分格式。若格式的网格节点全部在界面的一侧时,使用基础文献的四阶紧致差分格式(2),若格式的网格节点涉及界面两侧使用本文构造的四阶紧致差分格式,为了使整体能够达到四阶精度,在正侧点处添加修正项,进行修正,将其转化为负侧点,从而构造了一种新的四阶九点紧致差分格式(14)。最后,通过理论分析和数值验证可以得到该格式是可行的、可靠的。 表8 当k2−=25, k2+ =900 与k2−=100, k2+ =400 时,差分格式的误差与精度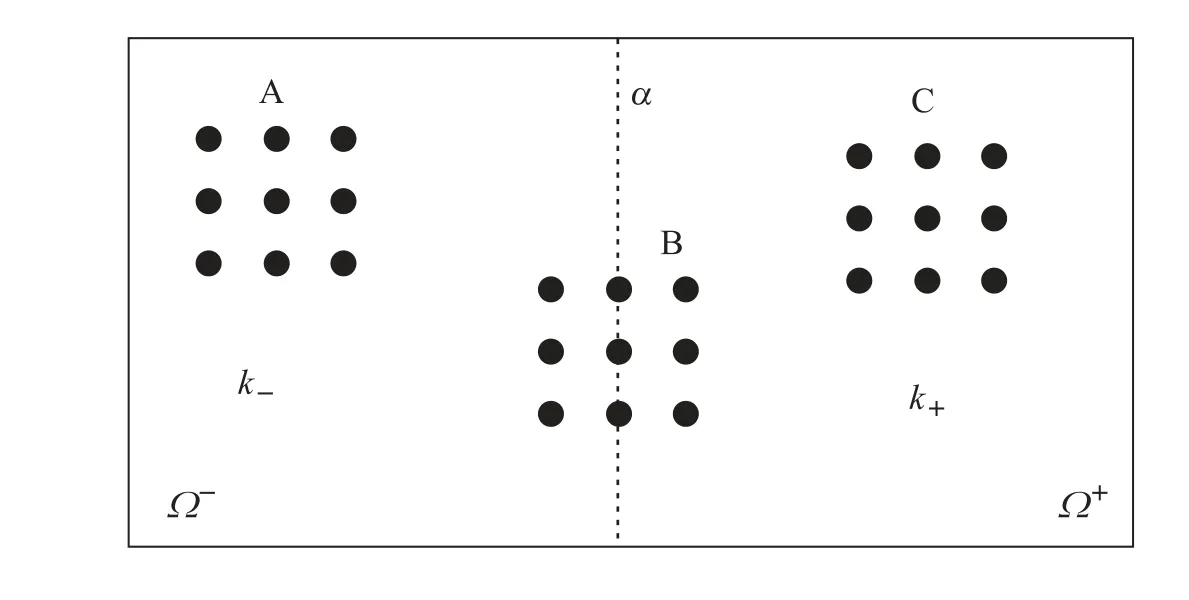







3 数值实验


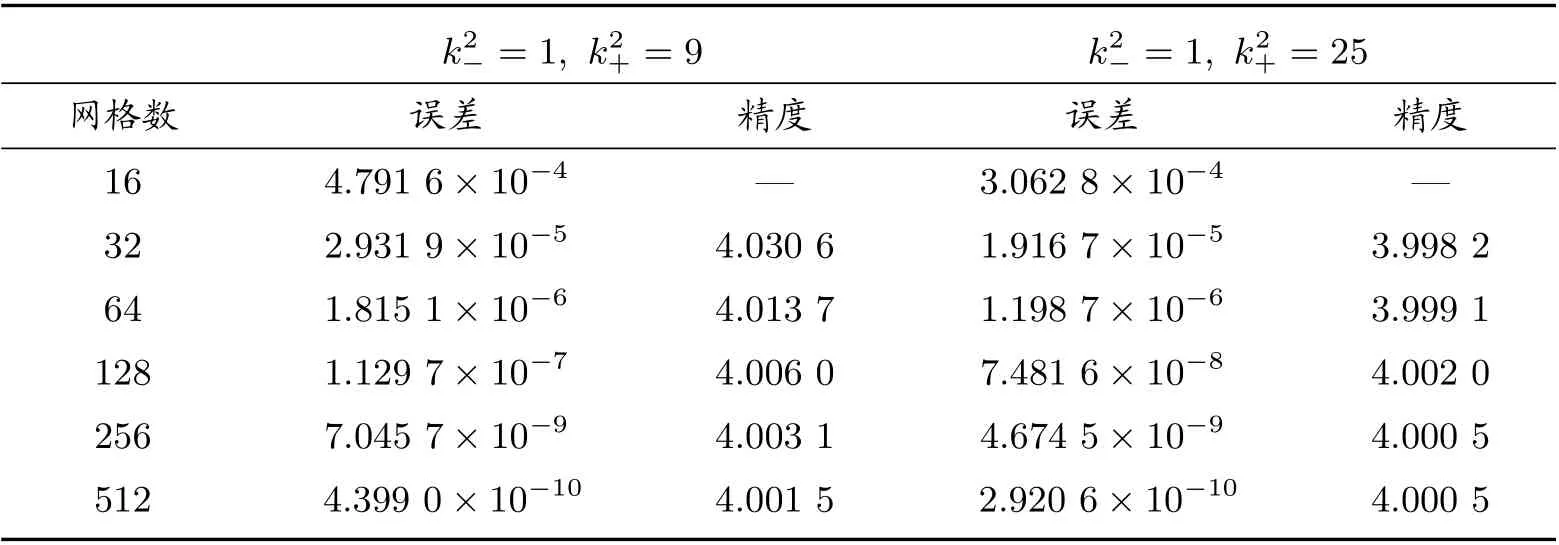
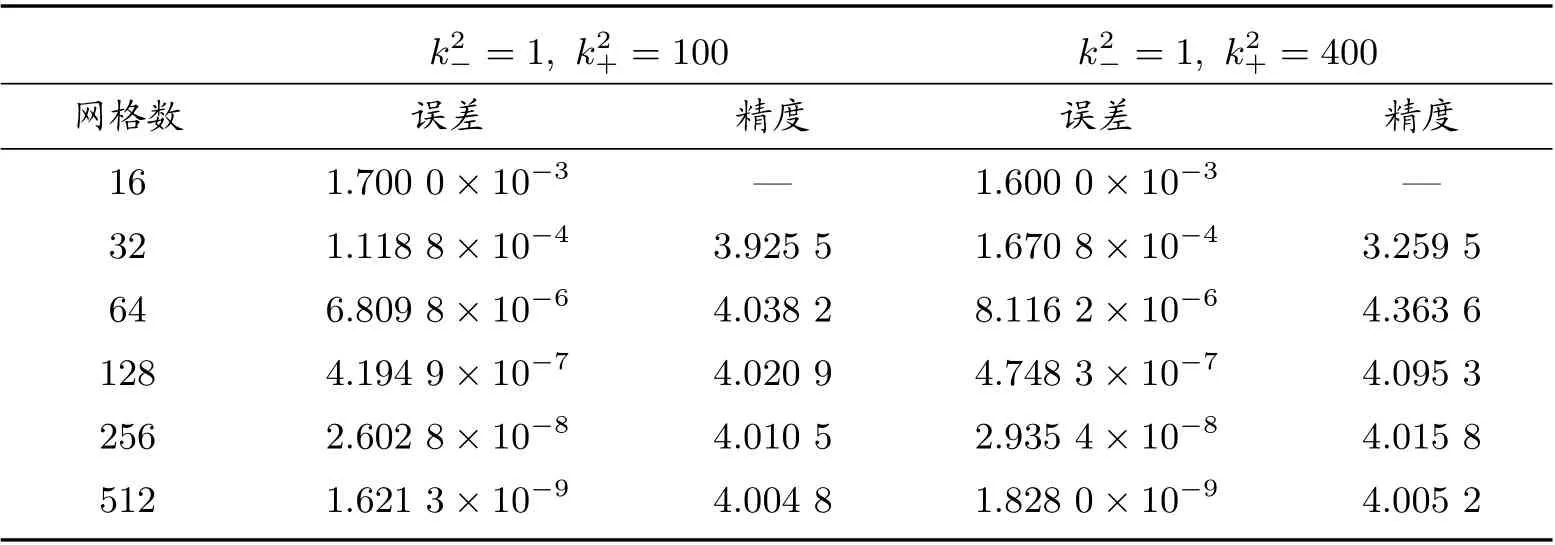
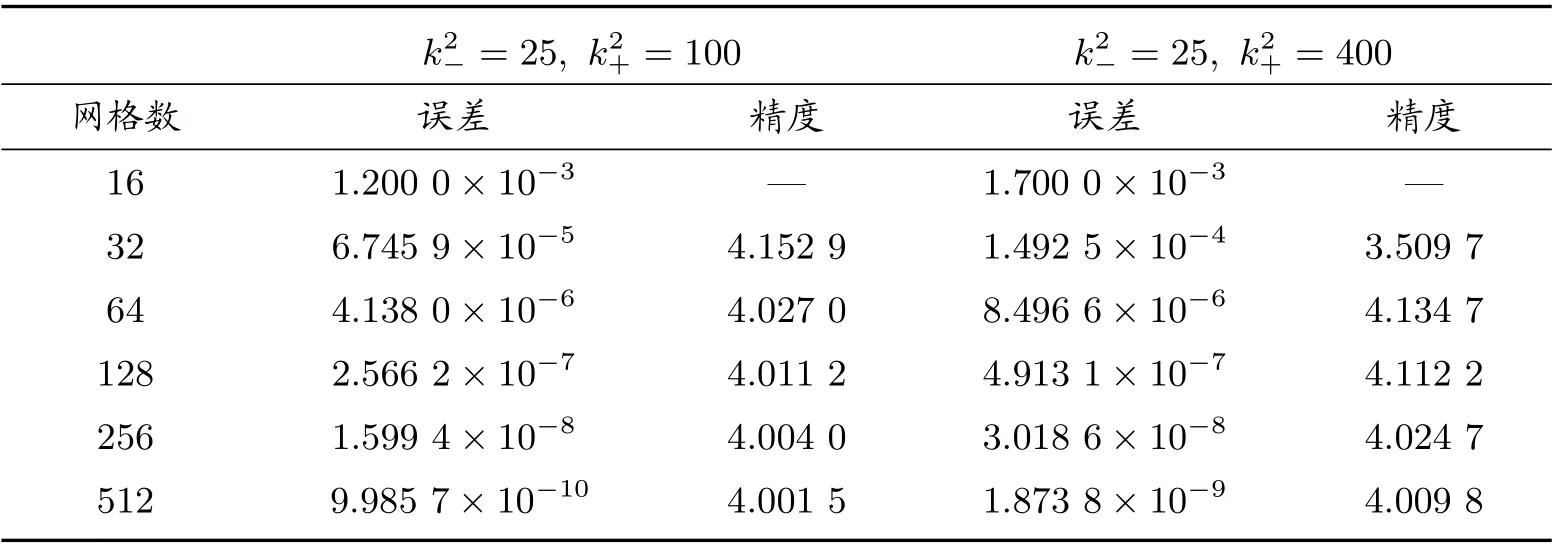


4 结论