磁通e-HR 神经元模型的放电行为及同步控制

马 杰, 高 洁, 独盟盟, 杨丽新

(陕西科技大学文理学院，西安 710021)

0 引言

生物神经元是构成复杂神经网络的基本结构和单元，具有丰富的放电行为，并且神经元之间信息的传递、交流等行为主要是通过神经元的放电活动进行的。文献[1]对e-HR 神经元模型进行了分岔分析和稳定性分析，并且对其存在的隐藏放电动力学以及控制同步进行了研究。文献[2]通过磁通变量来改进原HR 神经元模型，设计了一个四变量磁通HR 神经元模型来描述电磁辐射对神经元放电活动的影响。Song 等[3]研究发现，含有电突触比含有化学突触的HR 神经元的放电活动更容易被外部刺激诱发。文献[4]讨论神经元模型的分岔分析及其存在的隐藏吸引子，并对神经元模型的分岔进行控制。文献[5]以五维超混沌类系统为研究对象，根据Hopf 分岔理论和Routh-Hurwitz 理论，分析了系统非零平衡点的稳定性，以及分岔解稳定性。文献[6–7]对时滞耦合HR 神经元的同步以及部分同步进行实验，以改进的ML 神经元模型，对模型进行数值仿真，研究ML 神经元模型各种丰富的放电情况，另外研究了化学突触和电突触耦合这两种不同耦合方式下的同步控制问题。本文从数学角度对磁通e-HR 神经元模型进行了平衡点与Hopf 分岔分析，讨论了不同外加刺激电流和磁通反馈增益下神经元模型呈现出不同的放电模式。此外研究了磁通e-HR 神经元模型的控制同步，基于Lyapunov 稳定理论设计控制器，并从理论分析和数值模拟两个方面来说明控制器的有效性与可行性。

1 模型描述

最常见的神经元模型除了HH 神经元模型和HR 神经元模型外，在HR 模型的基础上考虑细胞内离子的转移，得到了e-HR 神经元模型，它具有和HR 神经元模型相似的特性。所以，基于e-HR 神经元模型，考虑外界电磁场对膜电位变化的影响，引入磁通量后建立的e-HR 神经元模型的微分方程如下

其中a、b、c、d、e、f、g、u、s、h、v、k、r、l为系统的参数，状态变量x表示神经元的细胞膜电位，y、z分别表示快电流和慢电流，w表示缓慢的动力学行为，φ表示穿过神经元细胞膜的磁通量，I表示外部刺激电流，k0表示磁通反馈增益，W(φ)是由磁通量控制忆阻器的记忆电导，其中W(φ)=α+3βφ2。

2 平衡点稳定性及Hopf 分岔分析

2.1 平衡点稳定性分析

若系统的平衡点为s∗=(x,y,z,w,φ)，通过化简可以得到

当系统取k0=0.2, I=1 时，系统的平衡点为S1=(−1.259 869 962,−6.504 001 479,1.360 520 15,−14.412 004 44,−2.267 765 932)，则系统在平衡点处对应的雅克比矩阵的特征值为

由特征值的正负性可知平衡点S1是不稳定的焦结点，且系统在平衡点S1处是不稳定的。

当系统取k0=2, I=1 时，系统的平衡点为S2=(−1.112 939 521,−4.904 744 852,1.948 241 915,−9.614 234 556,−2.003 291 138)，则系统在平衡点处对应的雅克比矩阵的特征值为

同理，可由特征值的正负性可知平衡点S2是稳定的焦结点，且系统在平衡点S2处是稳定的。在该系统中，稳定的平衡点对应静息态，不稳定的平衡点对应非静息放电模式。

以下讨论系统的稳定性，设系统的平衡点S∗= (x∗,y∗,z∗,w∗,φ∗)，则系统在平衡点处的雅克比矩阵为

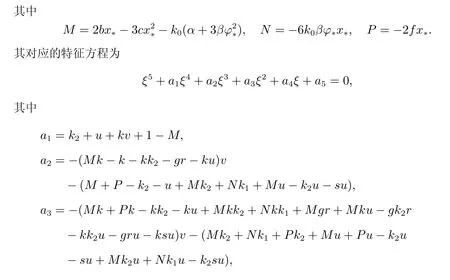
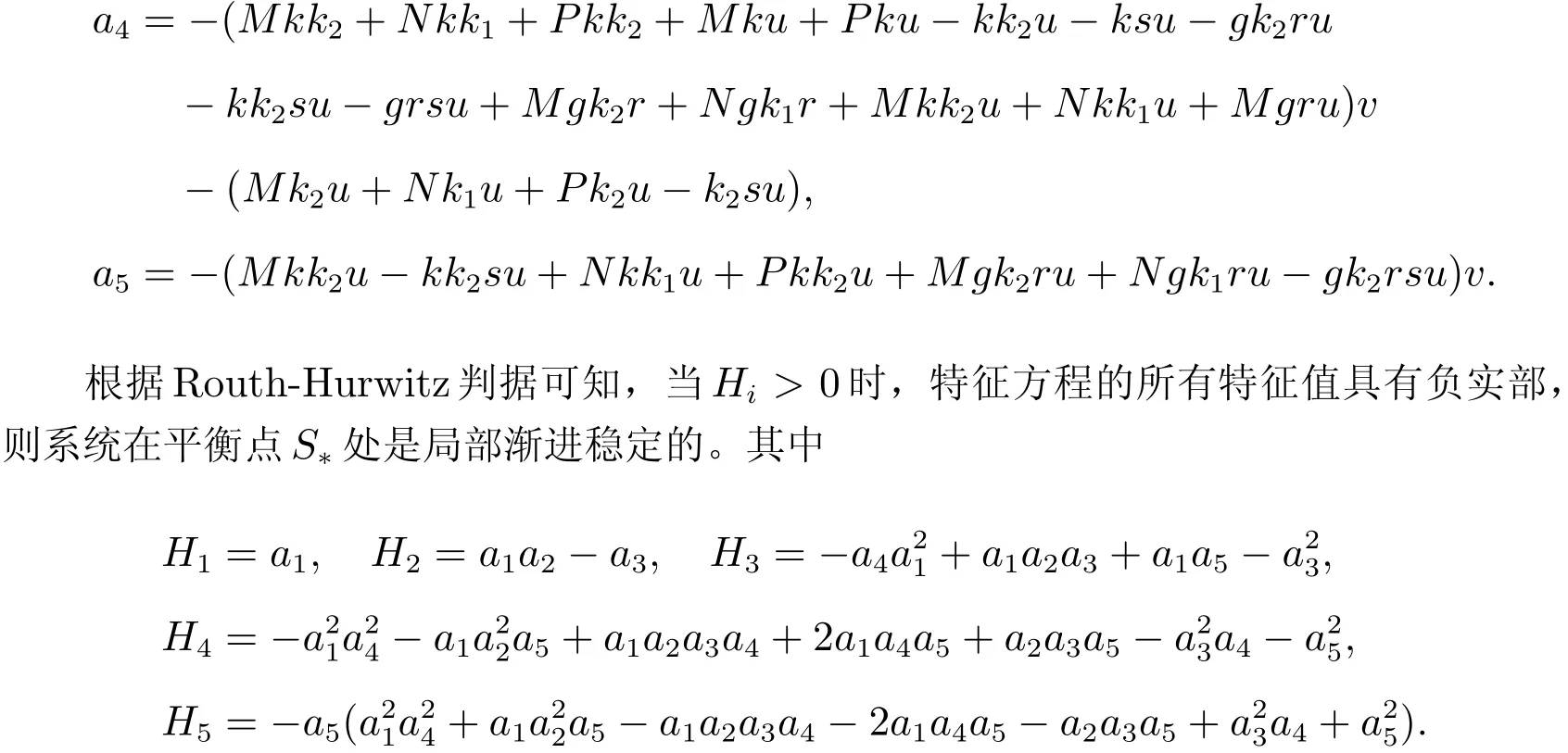
2.2 Hopf 分岔分析

为满足Hopf 分岔的存在及横截性条件，考虑特征方程关于参数k0的导数

2.3 放电行为模拟

数值模拟中，采用四阶Runge-Kutta 算法，通过选取不同的参数值可以得到膜电位的时间序列图，在不同的外加刺激电流下可以呈现出不同的放电模式。取初值为(0.1,0.1,0.1,0.1,0.1)，取反馈增益k0= 2，令α= 0.1, β= 0.02, k1= 0.9, k2=0.5，通过选取不同的外加刺激电流，可以得到神经元的不同放电模式，结果如图1 所示。

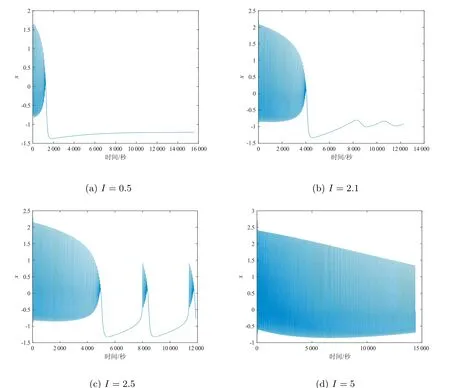
图1 外加刺激电流不同时，神经元膜电位的时间序列图

从图1 可以看出，当I=0.5 时，此时神经元的放电模式呈现静息态；当I=2.1 时，此时神经元的放电模式呈现静息态；当I= 2.5 时，神经元的放电模式呈现簇放电；当I= 5 时，神经元的放电模式呈现周期态。因此，在不同的外加刺激电流下神经元可以呈现出不同的放电模式。

神经元电活动行为不仅受到外加刺激电流的影响，并且与反馈增益参数k0也有着密切的联系。因此，在选定其他参数确定的情况下，施加外加刺激电流I= 2 的情况下，不断增大反馈增益参数k0，观察此时神经元的放电模式。

从图2 可以看出，当k0= 0.5 时，此时神经元的放电模式呈现周期放电；当k0=1.1 时，此时神经元的放电模式呈现簇放电；当k0= 1.8 时，神经元的放电模式为静息态；当k0=2.5 时，神经元的放电模式呈现静息态。因此，在不同的反馈增益参数下神经元可以呈现出不同的放电模式。

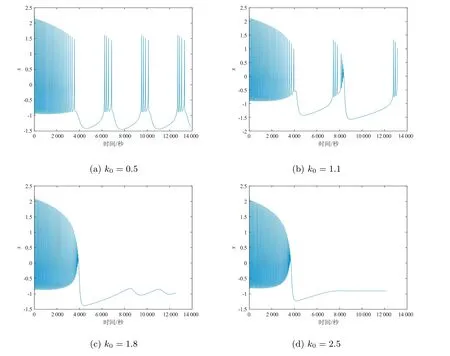
图2 反馈增益不同时，神经元膜电位的时间序列图

3 e-HR 神经元模型的控制同步

3.1 控制同步

同步控制是指通过系统自身的耦合或者施加外力等策略使得两个或者多个动力系统享受相同的动态行为。神经元同步时的耦合方式有很多种，如化学突触耦合、电突触耦合、磁通耦合等。本文通过建立网络化同步控制系统，简单的来说就是基于驱动–响应模式的网络化同步控制。设系统(4)为驱动系统

在外加刺激电流I1= 2.8, I2= 3 时，系统(4)与系统(5)表现出不同的放电模式，其相应的时间序列图，如图3 所示。为了使系统(5)同步到与系统(4)相同的状态，在系统(5)上施加了控制器，即U1、U2、U3。

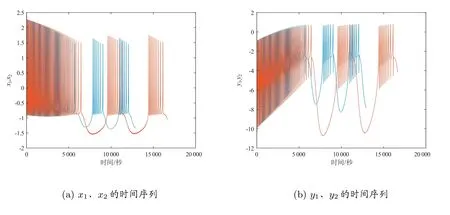
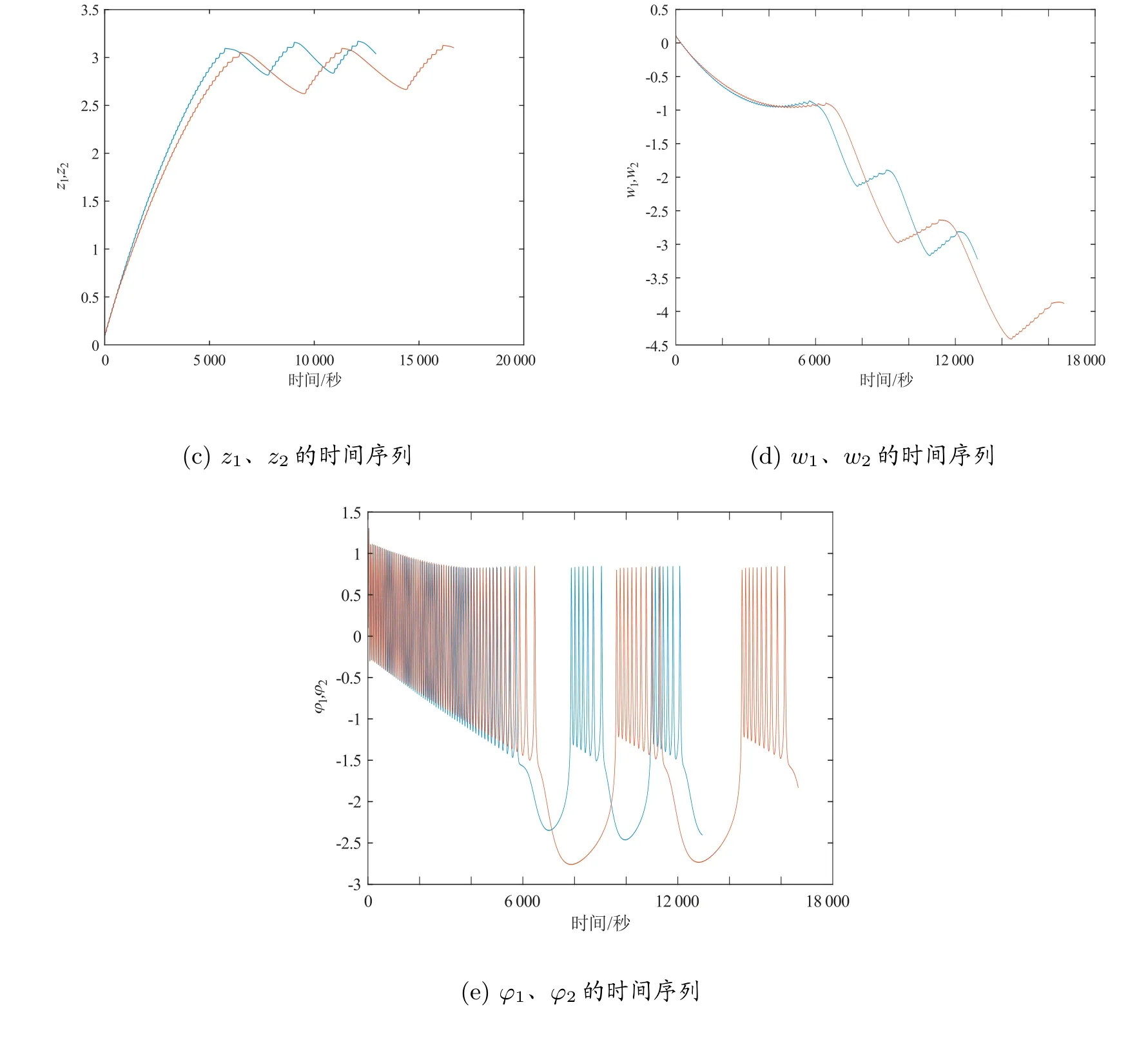
图3 时间序列图

定义系统(4)与系统(5)的同步误差为

所以根据(10)可知，当u>0, k2>0 时，˙V<0，从而可以得出误差系统(6)是渐近稳定的，进而得出系统(4)和系统(5)是同步的。

3.2 数值模拟

具体的数值模拟中取系统(4)的初值状态值为(0.1,0.1,0.1,0.1,0.1)，系统(5)的初始状态值为(0.1,0.1,0.1,0.1,0.1)。

当I1=2.8, I2=3 时，取其他参数不变，系统(4)与(5)呈现不同的放电模式，其相应的时间序列图和同步误差图，如图3 和图4 所示。

所以由图4 可知，在没有加入控制器之前，系统(4)和系统(5)分别保持着各自的动力学行为；加入控制器后，系统(4)和系统(5)在控制器U1、U2、U3的作用下达到了同步。

图4 加入控制器前、后系统(4)与(5)的同步误差图

4 总结

以引入磁通量后建立的e-HR 神经元模型为研究对象，分析平衡点个数以及稳定性，以及发生分岔的条件。发现改变外加刺激电流和反馈增益，神经元可以做出不同模式的响应即呈现不同的放电模式，如静息态、簇放电及周期放电；同时借助Lapunov 稳定理论设计满足同步的控制器且通过理论分析证明该控制器的可行性。关于其控制器是否满足时滞类神经元模型达到同步以及若引入时滞是否能够促进神经元模型更快地达到控制同步还需进一步了解。