非线性分数阶耦合泛函微分方程组边值问题的可解性

乔若楠, 刘锡平, 贾 梅

(上海理工大学理学院，上海 200093)

0 引言

在自然科学和工程技术的许多领域中，很多问题是用微分方程作为数学模型的。有些事物的变化规律不仅与系统当前状态有关，而且与它的过去和未来的发展状态有关。因此带时滞的泛函微分方程边值问题的理论研究受到广泛关注[1–9]。随着科学技术的迅速发展，分数阶微分方程在刻画一些非Newton 力学问题方面显示了特殊的优势。人们对分数阶微分方程进行了大量的研究[10–19]。近年来，分数阶泛函微分方程边值问题也得到了学者们的重视，并取得了很多研究成果[20–21]。

本文研究一类非线性分数阶耦合泛函微分方程组非齐次边值问题

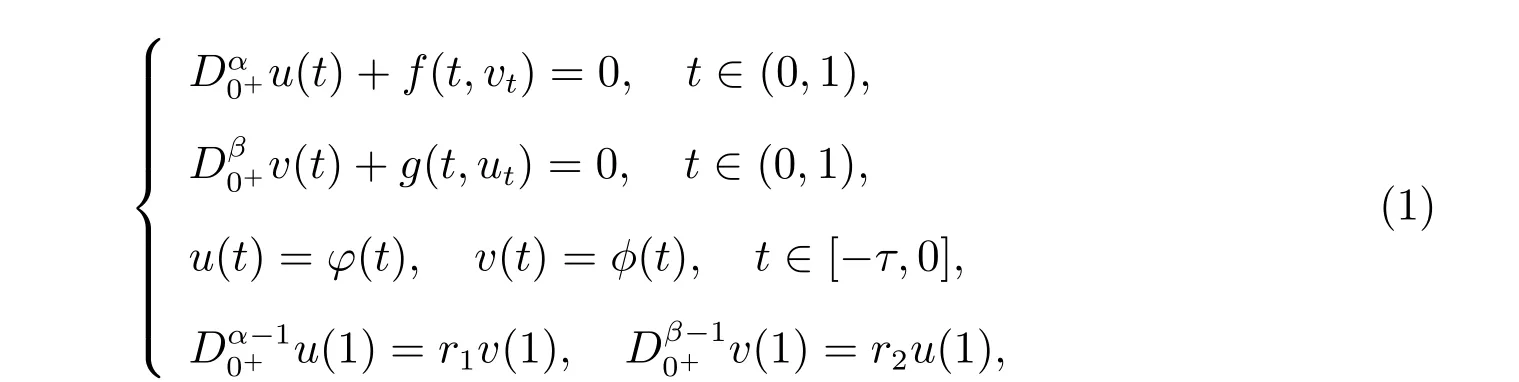
本文首先建立一个比较定理，然后运用上下解方法和迭代方法分别建立并证明了边值问题(1)正解的存在性定理和唯一性定理，并确定了正解的取值范围。最后给出一个例子证明结论的合理性。与现有文献不同是，本文所研究的方程组不仅在非线性项f和g中含有状态变量的泛函ut=ut(σ)=u(t+σ), vt=vt(σ)=v(t+σ)，而且是互相耦合，能更精确地描述一些控制过程。在解决方法上难度也更大，处理手法上也更具特色。

1 预备知识

2 解的存在唯一性

令P={(u,v)∈E:u(t)≥0, v(t)≥0, t ∈[−τ,1]}，则P为E上的正规锥。对任意(u1,v1),(u2,v2)∈E,(u1,v1)≼(u2,v2)，当且仅当(u2−u1,v2−v1)∈P。于是(E,≼)为半序Banach 空间。

定义1 设(u,v)∈E，若(u,v)=(u(t),v(t))满足(1)中各等式，那么我们称(u,v)是边值问题(1)的一个解。若当t ∈[0,1]时，u(t)≥0, v(t)≥0，则称(u,v)为边值问题(1)的一个正解。

定义2 设(u0,v0),(x0,y0)∈E。如果

于是，对任意t ∈(0,1)，都有h(t)≥0, l(t)≥0, a1≥0, a2≥0。

由引理2 可得边值问题

由引理4 可得，当t ∈[−τ,1]时，u(t)≥0, v(t)≥0。

为叙述方便，我们作如下假设：

则(x0,y0)≼(x1,y1)≼(u1,v1)≼(u0,v0)，且(u1,v1)、(x1,y1)分别是边值问题(1)的上解和下解。

证明 由引理2 可得(u1,v1)、(x1,y1)有定义。由上解的定义及(5)可得，对任意t ∈

由引理3 可得(u∗,v∗)∈P是边值问题(1)的正解。类似地，容易证明(x∗,y∗)∈P是边值问题(1)的正解。

假设(u,v)是边值问题(1)在Y中的解，则(x0,y0)≼(u,v)≼(u0,v0)。假设对任意正整数n都成立(xn,yn)≼(u,v)≼(un,vn)。与引理6 类似证明可证

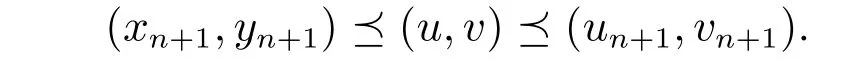
由数学归纳法可得，对任意n=0,1,2,···，有(xn,yn)≼(u,v)≼(un,vn)。

由迭代序列的收敛性可得(x∗,y∗)≼(u,v)≼(u∗,v∗)，所以(x∗,y∗)是边值问题(1)在Y中的最小正解，(u∗,v∗)是边值问题(1)在Y中的最大正解。

定理2 设0≤r1≤Γ(α),0≤r2≤Γ(β)，边值问题(1)存在上解(u0,v0)∈P和下解(x0,y0)∈P，且(x0,y0)≼(u0,v0)。若存在常数µ满足

3 例子

满足条件(S)，由定理1 可得，边值问题(15)在Y中有正解(u∗,v∗)、(x∗,y∗)，且(u∗,v∗)、(x∗,y∗)，分别是边值问题(15)的最大正解和最小正解。

容易验证对于0≤η<0.617 255，边值问题(15)满足定理2 的所有条件，由定理2 可得，边值问题(15)在Y中有唯一解。