MFC致动器的动态迟滞模型辨识及补偿控制
2022-05-30卢荣华陈特欢娄军强崔玉国
卢荣华, 陈特欢,2, 娄军强,2, 崔玉国
(1. 宁波大学 机械工程与力学学院,浙江 宁波 315211;2. 浙江大学 工业控制技术国家重点实验室,杭州 310027)
压电柔性结构具有质量轻,能耗低,可操纵性强等优点,已被广泛应用于航天探索,精密工程,柔性机器人等领域。但是,由于其固有的低阻尼比和较大的柔韧性[1],它们不可避免出现明显的持续振动,这会降低系统的定位精度和运行效率。因此,使用致动器柔性结构进行主动振动控制越来越受到人们的关注[2-3]。尤其在压电致动器的输入与输出之间存在迟滞效应,且不同压电致动器对不同频率的输入信号,其迟滞也不尽相同,对压电柔性结构精确控制,迟滞效应是必须考虑的主要因素。为了克服压电陶瓷的脆性,美国宇航局(NASA)发明了新型的基于纤维的压电复合材料(marco fiber composite,MFC)。MFC显示出优异的性能,如薄层压板,大驱动力和高可靠性[4-5]。Wu等[6]将MFC致动器应用到复合梁上,研究并获得其在空气中的静态与动态特性。
如今使用MFC致动器进行主动振动和变形控制受到广泛的关注。由于逆压电效应,压电陶瓷在电压输入下会产生变形。但是,其固有的迟滞和蠕变行为会降低驱动和定位精度[7]。此外,显著的迟滞效应甚至导致压电致动系统出现不稳定性问题。迟滞效应在驱动电压和响应位移之间呈现出环状非线性关系,压电致动器的迟滞问题亟需解决。目前描述迟滞的模型有很多,如基于物理现象,有Preisach(P)模型[8],PI(Prandtl-Ishlinskii)模型[9-10],Bouc-Wen模型[11],Duhem模型[12],Maxwell迟滞模型[13]。另外通过对模型优化,提出了一些改进模型,如基于PI模型进行改进的MPI(modified Prandtl-Ishlinskii)模型[14],基于传统Bouc-Wen模型引入形状控制函数进行优化,建立改进的Bouc-Wen模型[15]。在这些迟滞模型中,PI迟滞模型是目前应用最广泛的唯象模型,因为其实现过程相对简单,并且可以轻松获得其逆模型。指交叉电极技术允许MFC致动器在d33模式下工作。由于压电常数d33模式大约是d31模式的2~3倍,因此在d33模式下MFC致动器具更高的致动能力;另一方面,较大的致动力相应地需要较高的驱动电压。MFC致动器通常以很高的驱动电压驱动,甚至最高可达+1 500 V,从而产生强大的非线性动态响应。MFC致动器的复杂结构加剧了迟滞非线性,同时其迟滞具有明显的不对称性,故必须考虑MFC驱动的柔性臂的偏置双极性迟滞非线性,从而改善压电柔性臂的定位和操作精度。
大部分的迟滞模型均是静态的且输入频率低,无法满足高频率输入,也无法描述压电柔性结构的动态特性。如,Adly等[16]建立的广义PI模型,精确描述迟滞非线性,同时利用神经网络进行识别,模型局限于非线性需要一致性。Kuhnen[17]将迟滞算子与非对称迟滞环串行组合到经典PI迟滞模型中,建立一种改进型PI迟滞模型来描述非对称迟滞特性,但没有考虑输入频率对迟滞特性的影响。Wang等[18]提出一种MPI迟滞模型,采用耦合算子描述不对称迟滞特性,其仍是个准静态迟滞模型。相比动态迟滞模型,对不同频率迟滞适用性有限,且适用频率离压电致动器的固有频率较远。在动态特性方面,王钰锋等[19]基于Hammerstein模型,以MPI迟滞模型描述压电柔性臂的静态迟滞部分,以外因输入自回归模型描述压电致动器的迟滞线性动态部分,准确描述压电致动器的迟滞率相关。同时复杂控制器的引入,弥补逆补偿误差的问题,但易出现系统鲁棒性下降的可能性。Liu等[20]利用离散传递函数模型良好描述电力系统的动态特性,且系统是多输入多输出的。王一凡等[21]利用单输入单输出传递函数模型研究研究风电功率波动变化与换流站的动态关系。Liu等和王一凡等以传递函数模型进行系统的动态特性研究,为本文研究压电柔性臂迟滞的动态特性提供了一些思路。为了提高MFC致动器对不同频率输入的适用性,准确描述系统迟滞的动态特性。基于Hammerstein模型,建立具有双极性非对称的改进PI迟滞模型,同时建立系统的离散传递函数模型,串联组成一个组合模型。并设计相应的补偿控制方法,即前馈补偿控制。
本文搭建MFC致动的柔性臂构件试验系统,测试得到了柔性臂构件的末端变形位移与MFC致动器驱动电压之间的双极性非对称迟滞特性。基于经典PI模型,通过叠加一系列不同权重、不同阈值的双边死区算子,建立描述MFC致动器的双极性非对称性迟滞特性的改进PI迟滞模型,提高其迟滞模型非对称的逼近能力。在描述系统动态特性方面,采用离散传递函数模型描述系统线性动态特性,并与准静态改进PI迟滞模型串联组成组合模型,即压电柔性臂系统。最后,通过最小二乘法辨识得到改进PI迟滞正、逆模型,离散传递函数模型的特征参数,并对所提出的组合模型进行试验,结果表明其有效性。
1 MFC致动的柔性臂构件系统搭建
MFC结构组成示意如图1所示。MFC结构中环氧树脂的加入提升了整个复合结构的柔韧性、可靠性和变形能力,而指交叉电极的排布方式大幅提高了压电材料的应变致动效率。对比传统的压电陶瓷片而言,MFC的变形和驱动能力显著增强。因此,MFC致动器是柔性结构主动变形、驱动控制及振动抑制的理想元件。
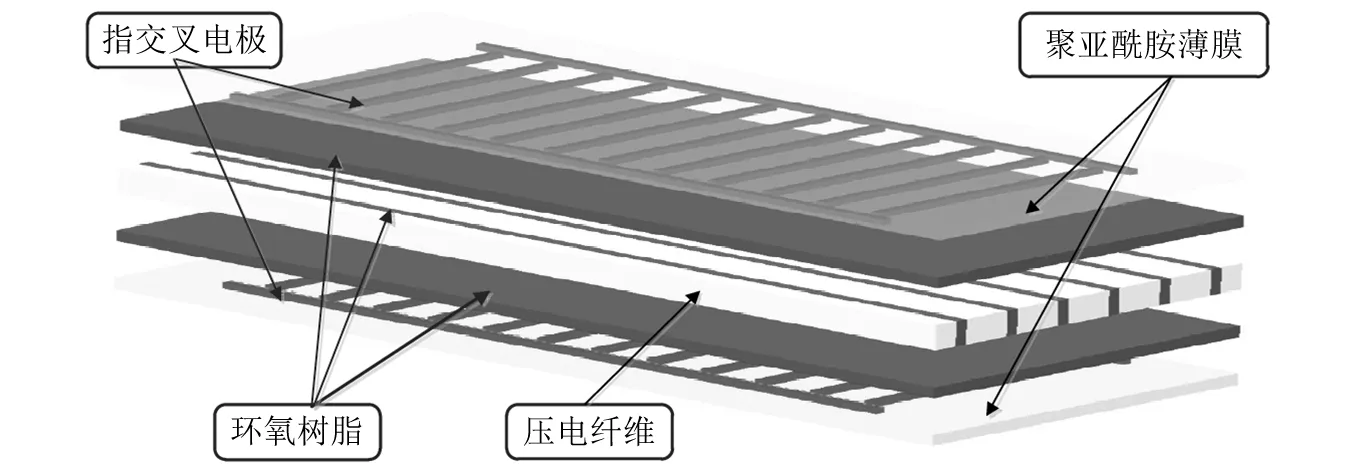
图1 MFC结构示意图Fig.1 Structure diagram of the MFC laminate
为了测试MFC致动器的致动性能,搭建MFC压电柔性臂构件试验系统,其实物图如图2所示。采用环氧树脂胶水3M-DP60将两片MFC致动器(型号M2814-P1,工作模式d33)对称地粘贴在铝基柔性臂构件根部的左右表面。柔性臂构件及MFC基本参数如表1所示。测试过程中,PC机通过USB总线将MFC致动器的驱动电压信号传输到多槽嵌入USB CompactDAQ机箱(NI,cDAQ-9178),然后经D/A模块(NI-AO9263)转换为模拟电压信号,该电压信号经高压放大器(Trek PZD700A,放大倍数200倍)放大后施加到MFC压电柔性臂上,MFC致动器在压电材料逆压电效应下实现柔性臂变形位移的精密驱动。水平安装在柔性臂构件末端的激光位移传感器(Keyence,LK-G80,分辨率0.15 μm)实时检测构件的变形位移,传感器检测位移经控制器调理为模拟电压信号,然后传输到嵌入在机箱中的D/A模块(NI-AI9205),最后经机箱和USB总线传输到PC机中。整个测试系统基于LabVIEW平台完成。

图2 试验装置实物图Fig.2 Photograph the experimental setup

表1 柔性臂构件及MFC致动器参数表Tab.1 Parameters of the beam and MFC actuator
MFC致动器的工作电压范围为-500~+1 500 V,故测试过程中选取电压峰峰值(voltage peak-to-peak,Vpp)分别为400 V、600 V及800 V,频率为0.1 Hz的正弦波驱动电压信号施加到MFC致动器上,得到柔性臂构件的末端变形位移与驱动电压之间的关系如图3(a)所示;不同频率在相同的输入电压下,压电柔性臂迟滞呈现迟滞的率相关,如图3(b)所示。试验结果表明:MFC致动器的驱动电压和柔性臂构件变形位移之间存在着严重的迟滞现象,不同激励电压下得到迟滞环的初载曲线基本重合。随着激励电压幅值的增大,迟滞现象愈加明显。在峰峰值电压800 V的正弦激励下,柔性构件位移的最大迟滞误差达50.6%。值得注意的是,在MFC致动器的双极性驱动电压作用下,柔性臂构件的正、负向变形位移存在着明显的偏置现象,且偏置随着驱动电压幅值增大而变大。在±400 V无偏置电压驱动下,柔性梁构件正、负向位移之间的偏置误差达24.4%。
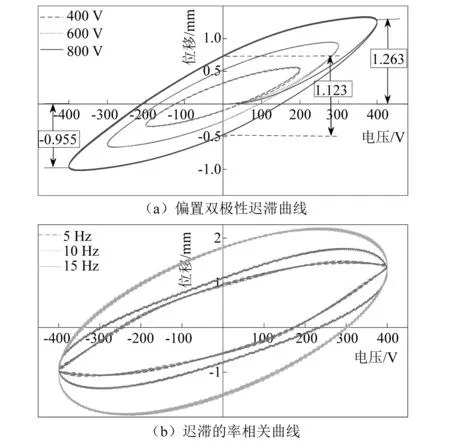
图3 MFC致动器的迟滞特性曲线Fig.3 Hysteresis loops of the MFC actuators
压电柔性臂的迟滞随着驱动电压频率增加也愈发明显,即呈现迟滞率相关性。此时准静态迟滞模型已无法良好描述不同频率的驱动电压在压电柔性臂的迟滞非线性特性,其显著影响了柔性构件的定位、操控。因此,迫切需要对MFC致动器的柔性臂的非对称迟滞特性及动态特性进行深入研究,对压电柔性臂模型进行辨识,并提出可靠的补偿控制方法来改善其驱动精度。
2 压电柔性臂的系统模型
对于压电柔性臂构件,其输入电压频率较低时(小于1 Hz),可以由准静态迟滞模型进行表示。故当输入驱动电压频率较大时,此时用单纯的准静态迟滞模型已无法准确描述系统的迟滞非线性特性,需要建立一个动态的迟滞模型来描述。基于Hammerstein模型的思想,提出一个组合模型描述系统的动态迟滞特性。该压电柔性臂的系统动态迟滞模型有两个部分,改进PI迟滞模型表示静态迟滞非线性部分;离散传递函数模型表示线性动态部分,如图4所示。

图4 试验对象系统结构框图Fig.4 Block diagram of the experimental object system
图4中:yc(t)为中间变量;u(t)和y0(t)分别为压电柔性臂的输入与输出。
2.1 改进PI迟滞模型
PI模型是目前应用最广泛的唯象迟滞模型之一,其表达式简单,求逆简便,易于实现。Play算子的数学解析式为
(1)
式中:l(t)为致动器的输入电压;yr(t)为其响应移;c代表常数;r及wr分别为Play算子的阈值和权重。
PI迟滞模型仅能描述压电柔性臂的对称迟滞特性。为描述压电柔性臂的双极性非对称迟滞特性,基于经典PI迟滞模型,串联一系列无记忆、非对称特性的死区算子。双边死区算子输入和输出之间的关系,如图5所示。
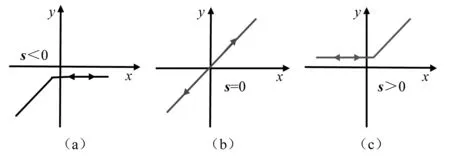
图5 死区算子的输入输出关系Fig.5 Input-output relationship of the dead-zone operator
双边死区算子的表达式为
(2)
式中,x(t)和Gs[x(t),s]分别为死区算子的输入和死区算子的输出,s为死区算子阈值,Gs=[G-m,G-m+1,…,G0,G1,…Gm]T为死区算子向量。将不同权重、不同阈值的死区算子进行叠加可得到G[x](t)
(3)
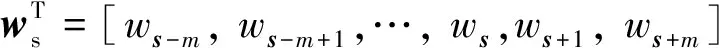
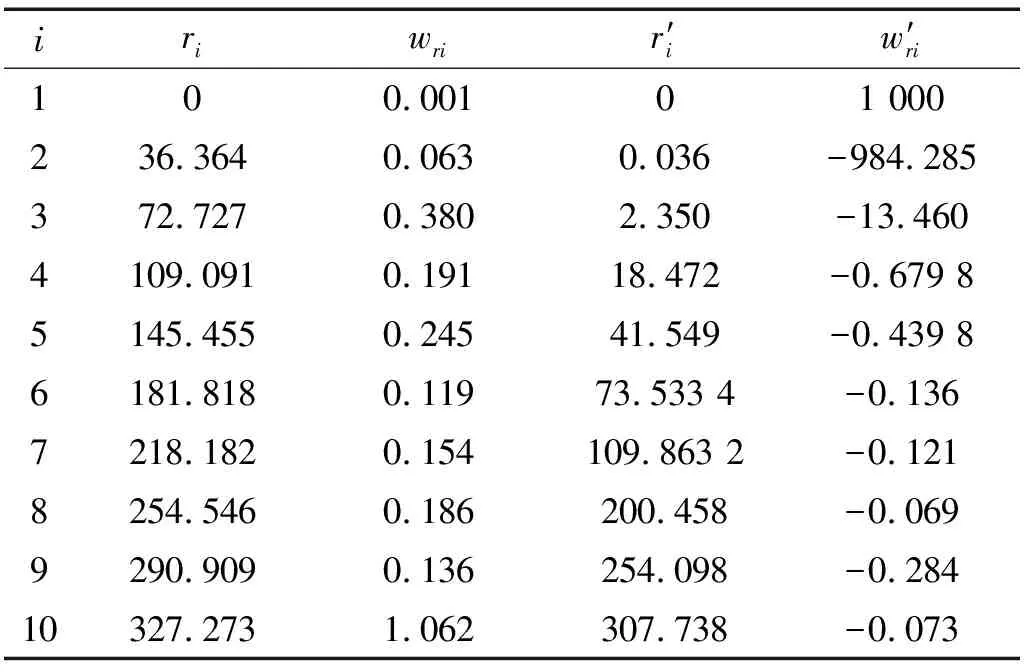
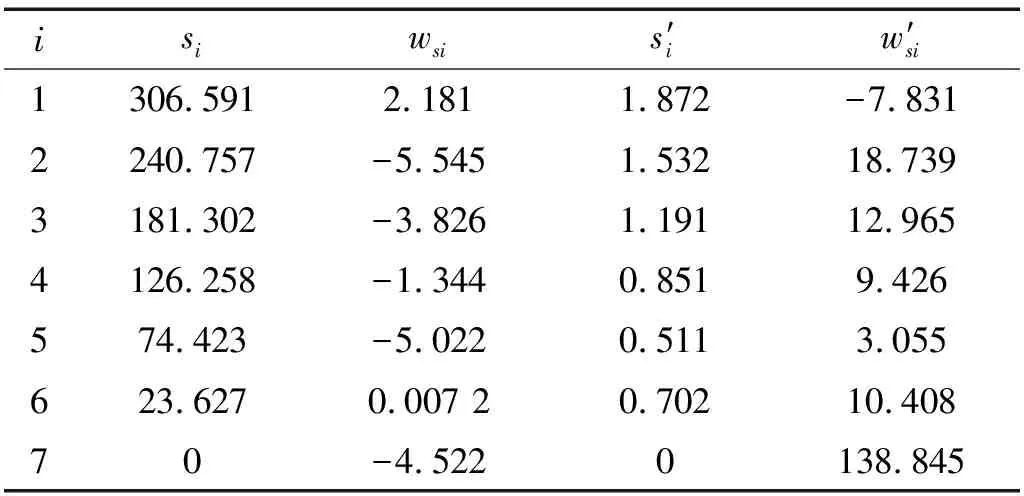
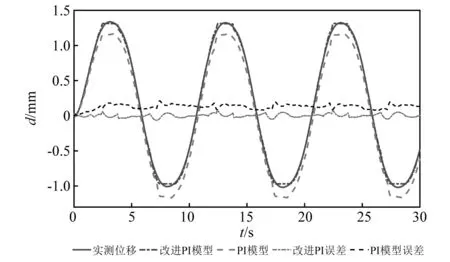
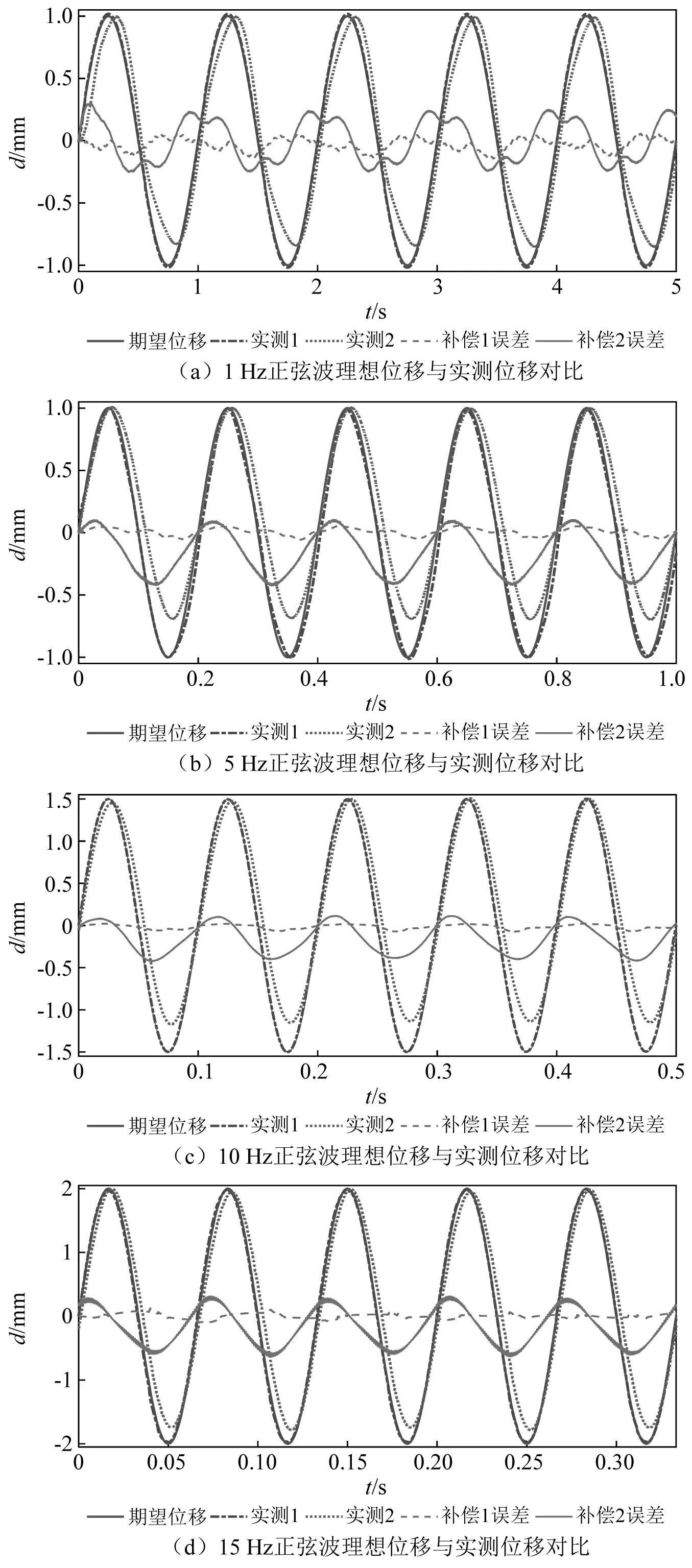
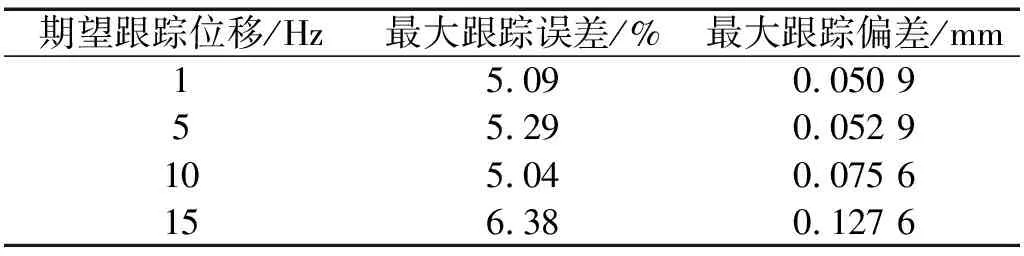
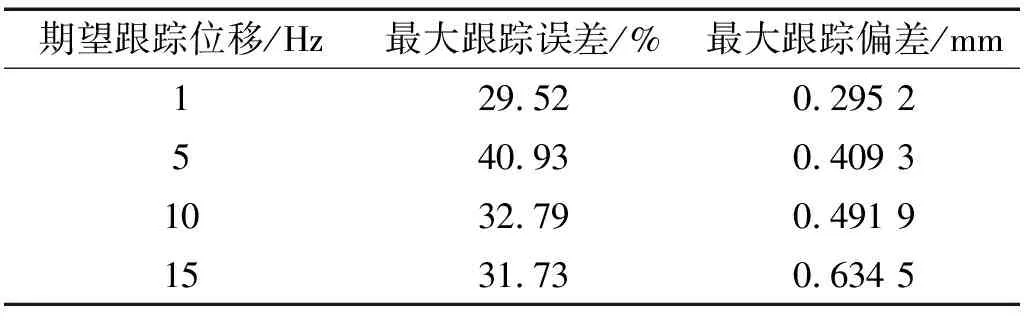
-∞ 综合上述,改进PI迟滞模型与经典PI迟滞模型的区别有:引入了死区算子及死区算子相关的权重、阈值;模型求逆时,出现死区逆算子的逆权重、逆阈值;动态迟滞模型是个组合模型,改进PI迟滞模型是准静态迟滞部分,另外引入离散传递函数模型描述动态迟滞特性部分。将Play算子与另一系列不同权重、不同阈值的双边死区算子进行串联,即可得到描述MFC压电柔性臂的迟滞现象的双极性非对称改进PI迟滞模型 (4) 压电致动器的固有特性,输入-输出关系必须保持强单调性,故对死区算子权重施加线性不等式约束来保证这一特性,如式(5)所示 Us·ws-us≤0 (5) 式中,us及Us矩阵如下 us=[-ε… -ε… -ε]T 式中,ε为无穷小量。 柔性臂和MFC致动器的参数如表1所示。描述压电柔性臂动态特性,需建立系统的动力学动态数学模型;同时建立系统的数学模型也是辨识的前提。纯改进PI迟滞模型,在描述迟滞的非对称性有明显改善,如图6所示。通过引入离散传递函数模型与改进PI迟滞模型串联成组合模型,能更好的描述迟滞动态特性。为研究方便,将柔性臂模型视作欧拉-伯努利梁模型,则离散传递函数模型使用多项式的比率描述系统的输入和输出之间的动态关系,其表达式为 (6) 式中,na和nb均为正整数。 采用最小二乘法对离散传递函数模型进行辨识。基于系统的输入和输出数据(见图4),得到如下最小二乘形式,即 yo(k)=φT(k)θ (7) 式中:φ(k)为数据向量,包括系统的输出和中间变量;θ为待估参数向量,具体表示为 (8) 基于系统采到的M组数据,利用最小二乘法得到其参数向量的估计θ*为 θ*=(φTφ)-1φTY (9) 式中:Y=[yo(1),yo(1),…,yo(M)]T;φ=[φT(1),φT(2), …,φT(M)]T。 由系统参数向量的估计为θ*,那么对应k时刻的估计输出为 (10) 将系统实际输出和估计输出之间的残差表示为 (11) 对系统采到的M组数据,其残差的平方和也就是性能指标,可以表示为 (12) 式中,e=[ε(1),ε(2),…,ε(M)]T。系统参数的最小二乘估计值就是对性能指标J求θ*向量的导数,并令其为0,从而计算得到参数使得J达到极小值。 为了辨识改进PI迟滞模型的参数,并求得死区算子的逆G-1[y(t)](t) (13) (14) 由式(2)中双边死区算子Gs[x(t),s]的输出与阈值正、负有关,故G[x](t)与G-1[y(t)](t)权重的转换关系为 根据试验所测得的MFC驱动电压与柔性臂构件位移之间的双极性非对称迟滞曲线,采用等分阈值的方式确定Play算子阈值ri和死区算子逆G-1[y(t)](t)阈值s′j为 (16) 式中,V为系统输入向量,即输入电压向量。 (17) E[x,y](t)= 表2 Play算子与其逆算子参数表Tab.2 Parameters of the Play operators and their inverse operators 表3 Play双边死区算子与其逆算子参数表Tab.3 Parameters of the double-sides dead zone operators and their inverse operators 从PI迟滞模型、改进PI迟滞模型与实测迟滞曲线拟合情况进行对比,如图6所示。Play算子对称平行四边形结构决定经典PI迟滞模型的输出正、负向位移也是对称的,故导致其无法很好地逼近迟滞曲线的正、负偏置位移,存在较大的偏差,最大偏差达214.5 μm,其拟合误差达到16.06%;而本文提出的改进PI迟滞模型是基于经典PI迟滞模型,引入不同权重、不同阈值的双边死区算子进行叠加,模型对比经典PI迟滞模型在非对称迟滞的逼近性能得到提升,其拟合的最大误差为74.5 μm,拟合度误差下降到5.58%。两种建模对比,改进PI迟滞模型更好的描述压电柔性臂的非对称迟滞非线性特性。 图6 PI迟滞模型与改进PI迟滞模型建模对比Fig.6 Modeling comparison between PI hysteresis model and improved PI hysteresis model 在辨识过程中,由于压电柔性臂的一阶振动模态在其振动中起主导作用,故对其振动进行一个截断处理,仅对振动的一阶振动模态进行辨识。 试验辨识采用幅值为±2 V,频率范围为10~30 Hz的正弦扫频电压信号,通过Labview测控平台驱动MFC压电柔性臂激起柔性臂的一阶振动,并使用激光位移传感器测量柔性臂末端的响应位移,整个扫频过程持续时间为20 s,采样频率为1 000 Hz。以改进PI模型的拟合位移(中间变量yc(t))作为输入,实测扫频响应位移作为输出,此时具有有限个数据点,对这些数据进行最小二乘法的拟合。由拟合结果,即可得到离散传递函数模型G(z),其扫频试验辨识结果如图7所示。试验结果表明,除了在压电柔性臂的固有频率附近拟合稍显不足,其余位置拟合度均较好。 从扫频辨识试验结果可得,离散传递函数模型与系统试验数据高度吻合,其拟合度可达95.39%,充分体现了离散传递函数模型对于压电柔性臂的适用性。一般情况下,在一定范围内随着模型阶次的增加,模型与曲线的拟合程度也会得到提高。另外,随着模型阶次的增加,模型参数辨识的计算量、系统复杂度也会增加,并有可能降低离散传递函数模型的鲁棒性。辨识过程中,对几组不同模型阶次的输入与输出拟合度进行对比分析,最终采用二阶离散传递函数模型已经可以满足使用要求,同时采用离散传递函数模型能克服数据隐藏缺陷,使模型更加稳定。基于最小二乘法所辨识得到的离散传递函数模型G(z)为:G(z)=(629z-1-628z-2)/(1-0.241 9z-1-0.735 5z-2)。 图7 扫频试验辨识结果Fig.7 Sweep frequency experiment identification result 利用建立的改进PI迟滞模型与离散传递函数模型计算得到MFC压电致动器的补偿控制输入,本质上就是对改进PI迟滞模型与离散传递函数模型求逆。由改进PI迟滞模型及离散传递函数模型与其逆互为反函数,式(4)的两层算子依次求逆得到 对离散传递函数模型进行求逆,可得到:G-1(z)=(1-0.241 9z-1-0.735 5z-2)/(629z-1-628z-2)。 为验证压电柔性臂辨识出来的迟滞模型与离散传递函数模型的有效性,建立试验装置平台(见图2),开展柔性臂构件在MFC致动下正弦波轨迹跟踪试验。分别采用幅值为±1,±1,±1.5,±2,对应频率分别为1 Hz,5 Hz,10 Hz,15 Hz正弦波理想位移信号。根据求得的改进PI迟滞逆模型式(19),结合逆离散传递函数模型G-1(z),计算得到每个时刻的补偿控制电压,同时测得压电柔性臂补偿后的位移并与正弦波理想位移进行对比。同时为了对比组合模型的补偿效果,开展基于经典PI迟滞模型的补偿试验,试验结果如图8所示。实测1代表组合模型补偿后的实测位移,补偿1误差就是其补偿后的误差。实测2代表经PI模型补偿后的实测位移,补偿2误差是其补偿后的误差。 经典PI模型补偿后,由于其本身算子是关于中心点对称,即求得的逆补偿电压也是对称的,补偿不掉压电柔性臂的迟滞非对称性,同时不同频率还出现不同程度的相位差,补偿后的误差也偏大。而组合模型的补偿解决了压电柔性臂补偿迟滞非对称的问题,实测跟踪位移与理想位移曲线基本重合,跟踪误差控制在6.38%以内。表明,MFC压电柔性臂的迟滞现象基本消除,基于改进PI迟滞模型与离散传递函数模型的组合模型的补偿方法对MFC压电柔性臂的迟滞特性有明显的改善,具体效果数据,如表4和表5所示。 图8 补偿后试验结果Fig.8 Experimental results after compensation 表4 基于组合模型的补偿控制效果Tab.4 Compensation control effect based on combined model 表5 基于经典PI模型的补偿控制效果Tab.5 Compensation control effect based on classic PI model 表4和表5中四个不同频率信号均为正弦波位移信号。本文所提出的改进PI迟滞模型与离散传递函数模型的组合模型,虽然在很大程度补偿掉MFC压电柔性臂的迟滞误差,提高了其驱动精度,但是并未完全消除其迟滞引起的误差。下一步的工作,有必要引进反馈控制算法,搭建前馈+反馈的复合控制平台,以进一步提高其驱动精度、定位精度。 本文基于经典PI迟滞模型,叠加一系列不同权重、不同阈值的死区算子,建立一种具有非对称迟滞特性的改进PI迟滞模型。基于Hammerstein模型的思路,建立系统的离散传递函数模型,并将改进PI迟滞模型与离散传递函数模型串联构成一个组合模型,解决了纯迟滞模型对不同输入频率的适用性差及无法良好描述系统迟滞动态特性的问题。在前馈控制策略下,MFC压电柔性臂的跟踪精度得到一定的提高。目前仍存在一些不足:比如前馈补偿无法完全消除迟滞引起的误差,抗干扰能力弱,被动控制等。后续研究有必要引进前馈+反馈的复合控制策略,进一步提高驱动、跟踪精度。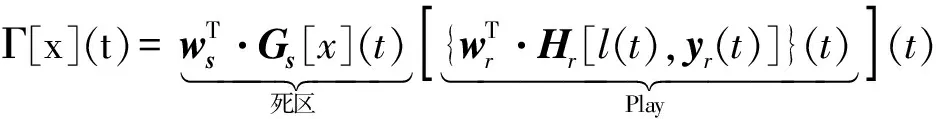
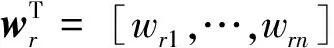
2.2 离散传递函数模型
3 模型的试验辨识
3.1 改进PI迟滞模型的辨识
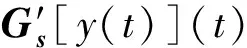
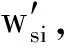
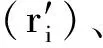
3.2 离散传递函数模型的辨识
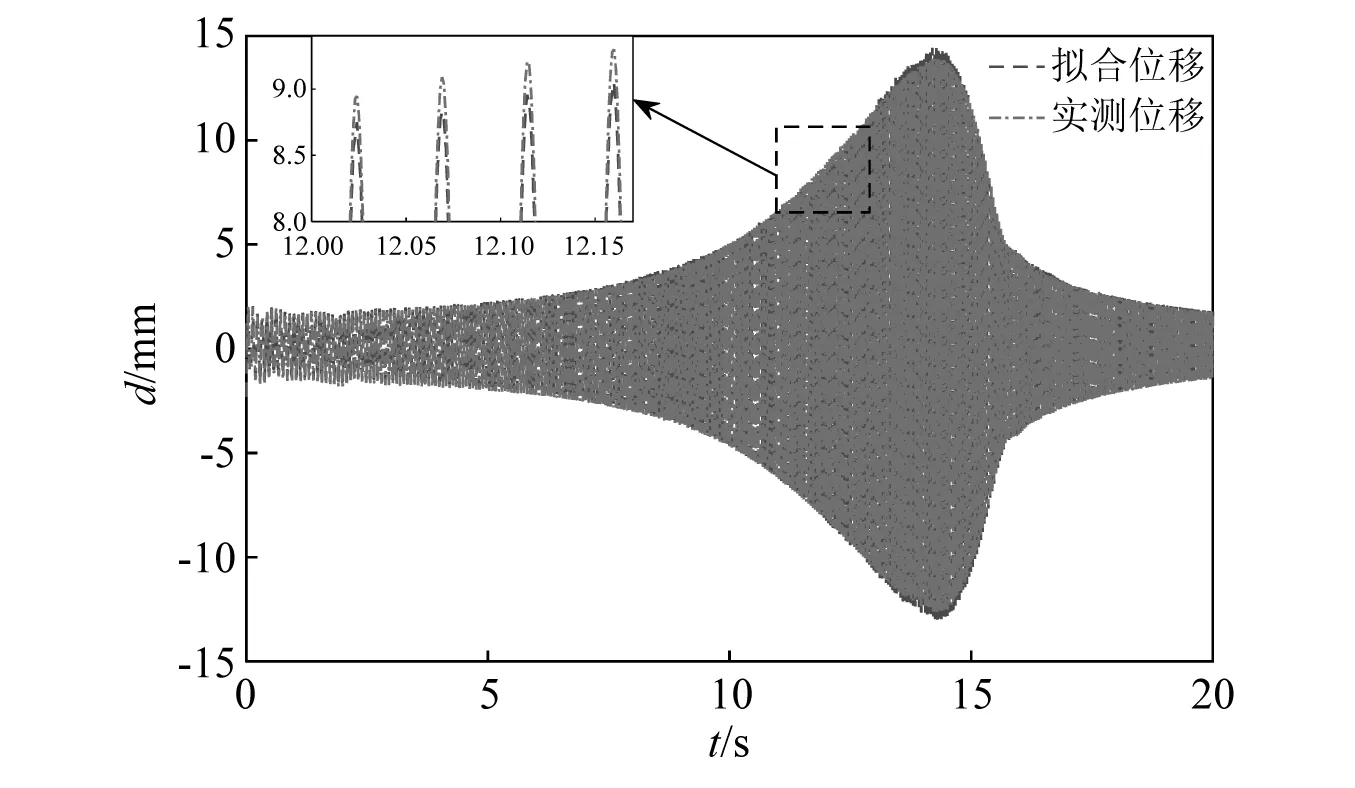
4 前馈补偿控制试验
5 结 论
