Infogram和参数优化CYCBD在滚动轴承复合故障特征分离中的应用
2022-05-30刘桂敏吴建德李卓睿
刘桂敏, 吴建德, 李卓睿, 李 祥
(1. 昆明理工大学 信息工程与自动化学院,昆明 650500;2. 昆明理工大学 云南省人工智能重点实验室,昆明 650500)
滚动轴承作为旋转机械设备的重要部件,在设备运行过程中起着至关重要的作用,一旦发生故障,轻则导致生产过程停滞,重则危及生命与财产安全[1-2]。在实际生产中,滚动轴承运行工况复杂,随着运行时间的增加,会出现两个以上的故障,即复合故障。在复合故障中,单一故障彼此影响,故障特征不易提取[3]。因此,研究行之有效的复合故障诊断方法才能准确提取故障特征、定位故障位置,是保障旋转机械安全稳定运行的关键[4]。
为实现滚动轴承复合故障的准确诊断,常常将复合故障分解为单一故障,增强单一故障特征[5]。然而,在故障分离过程中,振动信号受噪声污染,故障频率难以辨识,大大增加了故障特征分离的难度。如何对信号进行降噪处理是复合故障信号领域重要的研究方向之一[6]。目前,带通滤波器由于可以滤除频段内各种无用信号与噪声,降低频段之间的信号干扰得到了广泛应用。而在带通滤波过程中,中心频率用于确定故障频带的位置,带宽确定频带的宽度,带宽太小不能包含足够的故障特征频率信息,太大则会引入更多噪声干扰,因此,合理选择中心频率和带宽是有效降噪的关键[7-9]。快速谱峭度(fast kurtogram,FK)方法以谱峭度(spectral kurtosis,SK)理论为基础,可以有效筛选出包含故障冲击信息最多的共振频带,快速确定最优中心频率及带宽[10-11]。王宏超等[12]将FK算法用于带通滤波器参数的确定,有效提取了滚动轴承的故障特征,弥补了人工干预进行带通滤波参数确定的不足。但若信号的信噪比较低,或瞬态重复率较高,FK极易失效[13]。为此,Antoni[14]引入了谱负熵的概念,提出了Infogram方法,同时考虑了故障信号的冲击特性与循环平稳特性,弥补了峭度图方法的缺陷,提升了故障周期识别度。夏均忠等[15]将Infogram应用于滚动轴承故障诊断中,通过与FK的对比分析,证明了Infogram方法在选择共振频带方面的优越性。为此,本文引入Infogram方法对信号进行预处理,消除噪声干扰,获取冲击性和循环平稳性最强的频带信号,为后续故障分离奠定基础。
此外,在复合故障信号中,各类故障常以卷积的形式在传输过程中相互影响。导致强故障信号掩盖弱故障信号,造成故障漏诊。因此,需要对其做进一步的分离,提取出滚动轴承的各单一故障成分。最大相关峭度解卷积(maximum correlated kurtosis deconvolution,MCKD)方法能够通过解卷积消除或减弱传输路径对故障信号的影响,更好地识别周期性故障冲击信号[16]。杨斌等[17]将MCKD与总体局部均值分解方法(ensemble local mean decomposition,ELMD)相结合,先用MCKD提取信号中主故障成分,然后使用ELMD筛去主故障后,再用MCKD提取次故障,有效分离了复合故障。刘文朋等[18]通过不同周期下解卷积结果输出信号的多点峭度值确定故障周期后,利用MCKD算法实现了复合故障的准确分离。但MCKD输入参数较多,只有当所有参数都得到合理选取时,才能发挥其在提取周期性故障冲击上的优越性。CYCBD以最大二阶循环平稳指标(second-order indicators of cyclostationary,ICS2)为依据,能够有效提取含故障冲击成分的源信号,输入参数相比MCKD方法更少,恢复脉冲周期平稳源的能力更强[19]。赵晓涛等[20]利用CYCBD有效提取了滚动轴承含有强噪声的微弱故障信号特征。CYCBD是通过求解一个有限长的滤波器解卷积来恢复故障源,滤波器的长度对解卷积结果影响很大,过长的滤波器会降低算法效率,则有效选取滤波器长度可以更好的增强信号特征。传统的滤波器长度选择依靠人为经验,不能实现自适应[21]。为了实现滤波器长度的自适应选择,本文在CYCBD的基础上,引入包络谱稀疏度指标,用于评价故障信号解卷积处理的效果,优化CYCBD滤波器长度,提高算法速率。
综上所述,利用Infogram方法的优势,以最大包络谱稀疏度为优化目标确定CYCBD最佳滤波器长度,结合改进的参数优化CYCBD方法,提出一种新的复合故障特征提取方法,实现复合故障的有效分离。并利用三种不同的数据集验证了本文方法的适用性。
1 基本原理简介
1.1 Infogram原理
滚动轴承振动故障信号同时具有脉冲性和循环平稳性,Infogram方法采用谱负熵指标来量化重复瞬态特征,并定义信号频带上的熵值为谱熵。若轴承正常运转,系统平稳,熵值最大。如若出现故障,则系统失衡,熵值最小。谱熵指标变化与峭度指标变化相反,为使两者变化趋势相同,定义谱熵的负值为谱负熵[22]。
设长度为k的时域离散信号为x(n)(n=1,2,…,k),其平方包络SEx(n;f,Δf)定义如式(1)所示

(1)
式中: j为虚数单位;H(·)为希尔伯特变换;f为频带中心频率;Δf为频带宽度。谱负熵在时域及频域中的定义如式(2)、式(3)所示
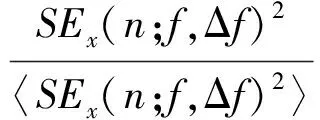
(2)
ΔIE(f;Δf)=
(3)
式中: 〈·〉为计算平均值;α为循环频率,表示频率变化值;SESx(α;f,Δf)为SEx(n;f,Δf)的傅里叶变换,即:SESx(α;f,Δf)=F[SEx(n;f,Δf)]。
时域谱负熵可以度量故障信号的冲击特性,频域谱负熵可以度量故障信号的循环平稳特性。基于熵的不确定原理,对两者进行加权平均,计算信号的平均谱负熵ΔI1/2(f;Δf)(如式(4)所示),则可以同时度量信号的冲击特性及循环平稳特性。
(4)
为便于计算和表示,Infogram采用短时傅里叶变换(short-time Fourier transform,STFT)构建滤波器组,将信号分解为不同层级。频率轴(横轴)按(Δf)i=Fs/2i规律进行分段,其中i代表分解层数,允许取非整数值。取STFT长度的典型值Nw=2,4,6,8,12,16,24,32,48,64对信号进行分解,则对应的i值为log2(Nw),即:1,2,2.6,3,3.6,4,4.6,5,5.6,6。计算分解后不同频带的平均谱负熵值,构造平均Infogram。其中,横轴表示信号的频率,纵轴表示分解层数,颜色深浅表示平均谱负熵值大小[23]。
1.2 CYCBD方法
CYCBD是一种基于广义Rayleigh熵的盲解卷积方法,以ICS2最大化为目标,通过迭代特征值分解算法求解,从而达到提取故障特征的目的。CYCBD通过对含噪观测信号x进行解卷积运算,获取具有循环平稳性的目标源信号s0,即
s=x*f≈s0
(5)
式中:s为源信号;f为滤波器; *为卷积运算符。用矩阵形式表示则为s=Xf,如式(6)所示

(6)

(7)
(8)
(9)

(10)
信号中周期成分矩阵的表达式如式(11)所示
(11)
则由式(6)、式(10)及式(11)可以得到ICS2的表达式,具体如式(12)所示
(12)
加权矩阵W如式(13)所示
(13)

CYCBD算法流程图如图1所示。具体步骤如下:
步骤1初始化滤波器f,迭代次数n=1;
步骤2由输入信号x和滤波器f计算输出信号s;
步骤3计算对应的加权矩阵W;
步骤4解出最大特征值λ对应的滤波器f;
步骤5返回步骤2,直至ΔICS2≤ε或n≥100;
步骤6进行解卷积运算,输出目标源信号s。
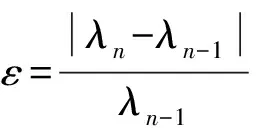
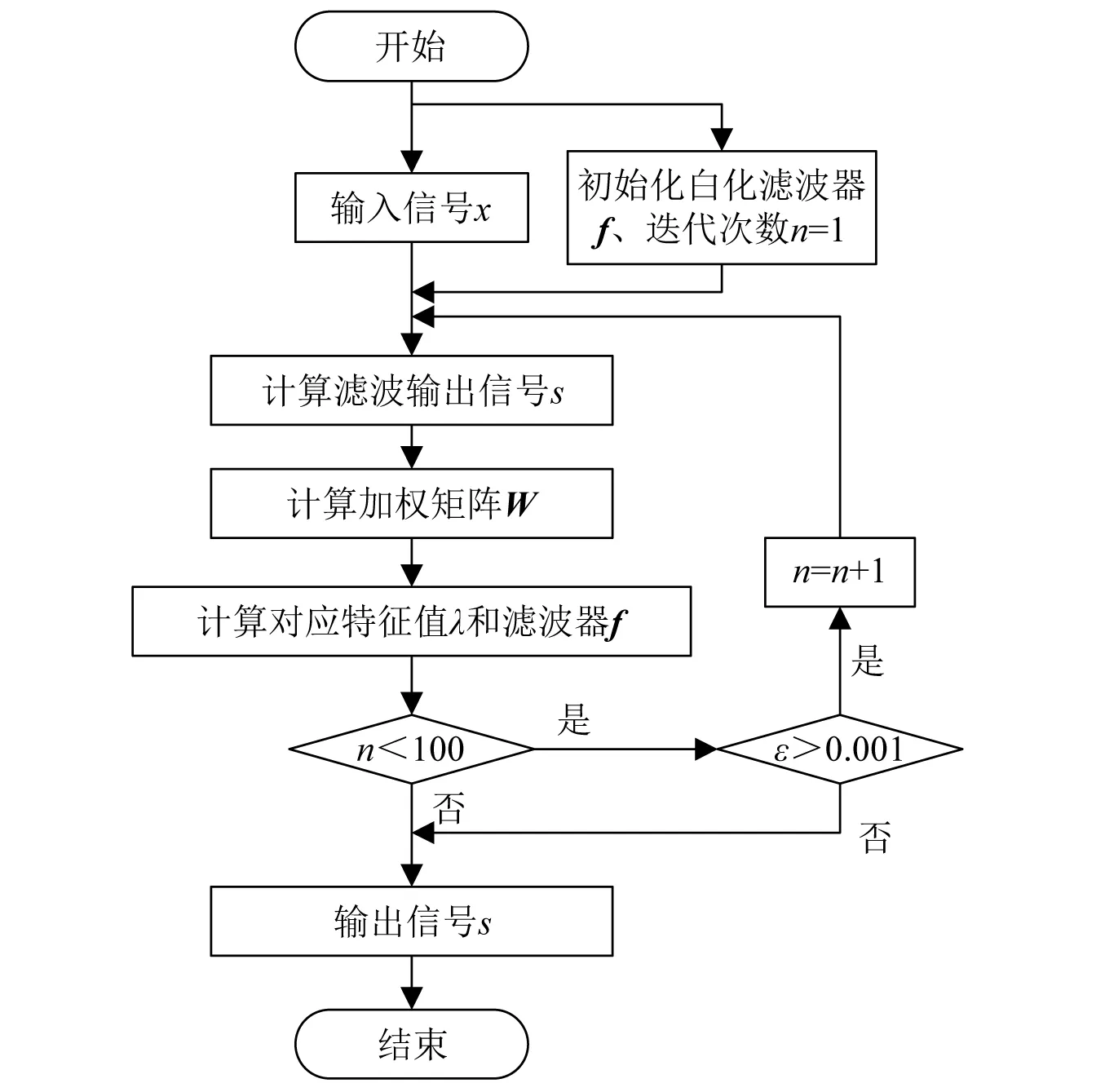
图1 CYCBD算法流程图Fig.1 CYCBD algorithm flow chart
1.3 参数优化CYCBD
CYCBD的分析效果受滤波器长度的直接影响,而滤波器长度的变化趋势与指标ICS2值的变化趋势基本一致。滤波器长度增加,ICS2值会随之变大,但计算所需的时间也会变久。若在一定范围内依据最大ICS2来确定滤波器长度,则会选择该范围内的最大值,大大降低算法效率。为了提高计算效率,需要选定适合的指标确定最优滤波器长度。本文以包络谱稀疏度为依据,对滤波器长度进行自适应选取[24]。稀疏度是表征信号稀疏性的统计参量,可用于评价信号的解卷积效果。信号x(n)的稀疏度表达式如式(14)所示
(14)
当滚动轴承处于正常状态时,观测到的振动信号比较平稳,幅值大小基本一致,稀疏度较小。一旦发生机械故障,会出现离散峰值,使稀疏度增大。然而使用时域信号进行分析时,稀疏度极易受少数幅值较大的脉冲影响,不能很好反应解卷积效果,若将时域信号转换到频域,采用包络谱的稀疏度可有效评价解卷积效果[25]。对信号进行CYCBD处理后,若解卷积信号的包络谱中各处幅值大小基本一致,说明其包络谱的稀疏性较小,无明显故障信息;若包络谱的某些频率处出现离散峰值,则稀疏度将会增大,说明该信号中包含明显的故障脉冲[26]。
基于以上分析,本文以最大包络谱稀疏度为优化目标自适应确定CYCBD的滤波器长度,具体优化流程如下:
步骤1根据轴承结构参数计算滚动轴承各部件理论故障特征频率,并以此为依据,设置CYCBD的循环频率集。
步骤2设定搜索范围。为加快搜索速率,减少不必要的运算,CYCBD最小滤波器长度要能包括故障冲击信号衰减周期且不能太长,本文将滤波器的搜索范围定为100~1 000[27]。
步骤3在100~1 000搜索范围内以100为步长进行粗略搜索,以包络谱稀疏度最大值确定粗略的滤波器长度,并以此为界,在小于该长度100的范围内以10为步长进行精确搜索,确定CYCBD的最佳滤波器长度。
2 故障特征分离方法流程
本文提出的Infogram和参数优化CYCBD的复合故障特征分离方法流程图如图2所示。具体步骤阐述如下:
步骤1用Infogram对输入信号x(t)进行分析,根据平均Infogram中平均谱负熵最大的频带确定带通滤波器的中心频率fc和带宽Bw;
步骤2用确定的带通滤波器对输入信号x(t)进行滤波,获得降噪后的信号x1(t);
步骤3设定合适的循环频率集,计算不同滤波器长度下滤波信号的包络谱稀疏度,确定CYCBD的最优滤波器长度;
步骤4采用参数优化CYCBD对降噪后的复合故障信号x1(t)进行分析,得到解卷积信号;
步骤5对得到的解卷积信号包络解调分析,提取故障特征,确定故障类型。

图2 Infogram和参数优化CYCBD的故障特征分离方法Fig.2 Fault feature separation methods for Infogram and parameter optimization CYCBD
3 仿真信号分析
为验证本文所述方法的有效性,采用不同故障激起多个相同及不同共振频带的复合故障仿真模型[28],建立复合故障仿真信号(如式(15)所示),采样频率fs为25.6 kHz,分析点数为10 240点。
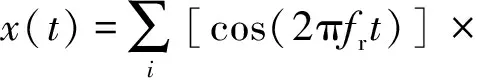
(15)
式中:n(t)为信噪比为-5 dB的高斯白噪声;i为故障周期数;其他参数设置如表1所示。

表1 仿真信号参数Tab.1 Parameter of simulation signal
仿真信号时域波形如图3所示。从图3(c)的复合故障信号中已无法看到图3(a)和图3(b)中明显的周期性脉冲成分。对时域信号进行STFT及包络解调分析,得到的频谱与包络谱如图4所示。在图4的频谱及包络谱中均未找到相应的故障特征频率,可见背景噪声严重影响了信号故障特征的提取,采取常用的信号分析方法无法实现复合故障特征的分离与诊断。

图3 仿真信号时域波形Fig.3 Simulation signal time domain waveform

图4 仿真信号频谱、包络谱Fig.4 Spectrum and envelope spectrum of simulation signal
为了实现复合故障分离,运用本文提出的方法进一步分析。首先得到复合故障信号的平均Infogram,如图5(a)所示。从图5(a)可知,平均谱负熵值最大的频带中心频率fc为9 600 Hz,带宽Bw为266.67 Hz。因此,设置最优带通滤波器的中心频率fc为9 600 Hz、带宽Bw为266.67 Hz,获得滤波后信号的时域波形及其包络谱如图5(b)所示。由图5(b)可知,复合故障信号中两种故障混杂在一起,不利于故障识别。

图5 平均Infogram及优选频带时频域波形Fig.5 Average Infogram and optimize frequency band time domain and frequency domain waveform
以最大包络谱稀疏度为评价指标,对CYCBD的滤波器长度寻优,采用参数优化后的CYCBD方法对信号进行分离。分离外圈故障时,根据外圈理论故障频率,设置循环频率集为[110,220,…,1 100],在设定的搜索范围100~1 000内寻优,寻优结果如图6(a)所示。从图6(a)可知,包络谱稀疏度最大值对应的滤波器长度为500。设定精细搜索范围为400~500,在此范围内继续搜索,包络谱稀疏度的变化趋势如图6(b)所示。从图6(b)可知,最优滤波器长度为500。因此,将CYCBD的滤波长度L设置为500,提取到的信号时域波形及包络谱如图7所示。从图7可知,信号包络谱中存在明显的外圈故障基频(110 Hz)及其倍频(2~13fo),外圈故障被成功分离出来。

图6 外圈滤波器长度优化过程Fig.6 Filter length optimization process for outer ring fault
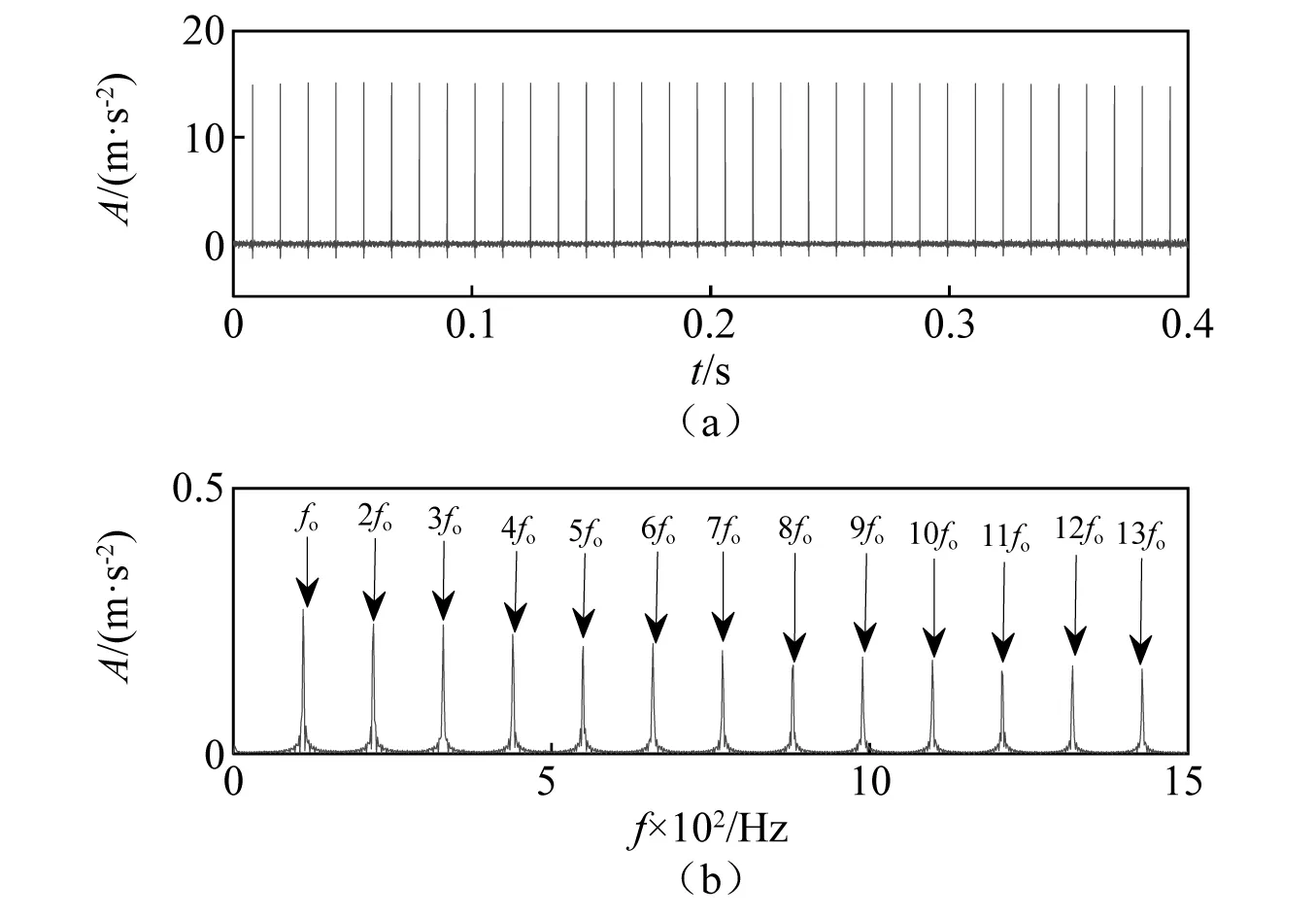
图7 外圈故障信号时域波形及包络谱Fig.7 Time domain waveform and envelope spectrum of outer ring fault signals
同样,在分离内圈故障时,根据理论故障频率设定循环频率集[180,360,…,1 800],在既定的范围内寻优,结果如图8(a)所示。从图8(a)可知,滤波器长度L为500时包络谱稀疏度最大。在400~500内继续寻优,结果如图8(b)所示。从图8(b)可知,最佳滤波器长度L应选为480。将CYCBD算法的滤波器长度设置为480,提取到的内圈信号时域波形及其包络谱,如图9所示。
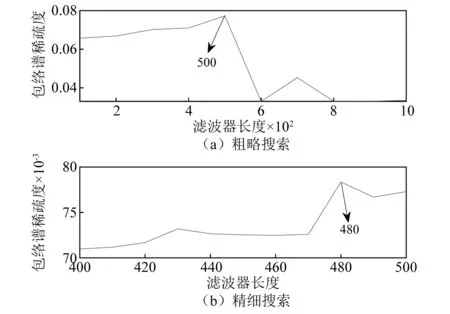
图8 内圈滤波器长度优化过程Fig.8 Filter length optimization process for inner ring fault
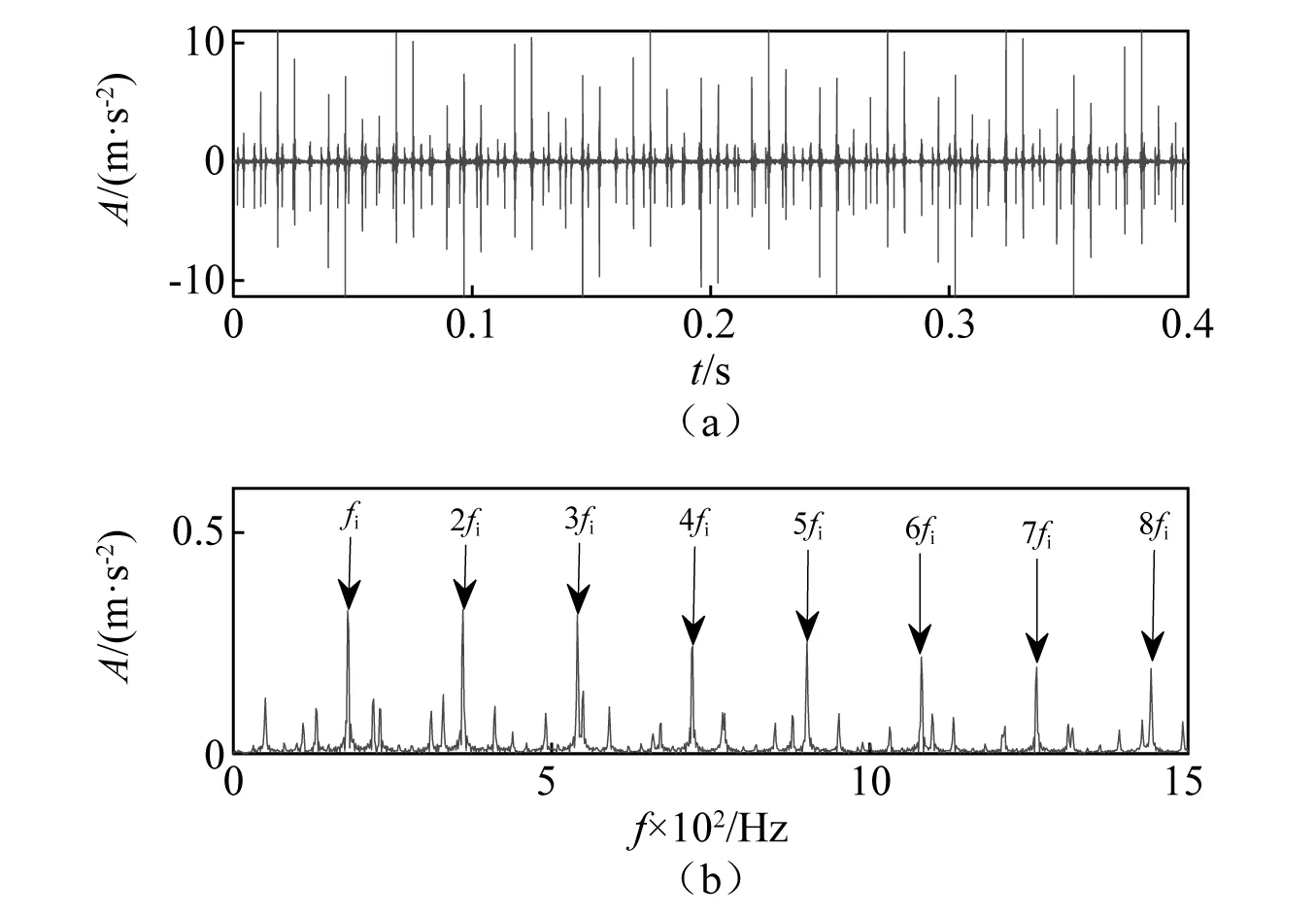
图9 内圈故障信号时域波形及包络谱Fig.9 Time domain waveform and envelope spectrum of inner ring fault signals
从图9可知,包络谱中包含清晰的内圈故障特征频率(180 Hz)及其倍频(2~8fi),内圈故障信号被成功分离出来。
综合以上分析可以确定,该信号同时包含内圈和外圈故障信息。本文所提方法在强噪声干扰下,有效提取了复合信号包含的全部故障特征,实现了外圈和内圈故障特征的分离。
4 试验验证分析
为进一步论证该方法的有效性,使用西安交大-昇阳科技联合试验室(Xi’an Jiaotong University-Changxing Sumyoung Technology,XJTU-SY)滚动轴承试验数据进一步分析。并使用自制试验平台完成了复合故障试验,对所提方法进一步论证。
4.1 XJTU-SY轴承数据试验分析
XJTU-SY滚动轴承试验平台如图10所示,包括交流电动机、转速控制器、转轴、液压加载系统和测试轴承等部件[29]。其中,测试轴承是型号为LDK UER204的滚动轴承,轴承具体参数如表2所示。试验的采样频率fs为25.6k Hz,转速为2 100 r/min。轴承故障特征频率可以通过式(16)和式(17)进行计算
(16)
(17)
式中:n为滚动体个数;d为滚动体直径;D为轴承节径;α为接触角;fr为轴承转速。计算得fi=172.09 Hz,fo=107.91 Hz。本文采用工况1数据集中内外圈复合故障数据进行试验分析,信号时域波形及其频谱如图11所示。从图11可知,时域波形中无明显的周期性冲击成分,频谱中也无明显的故障频率。

图10 轴承加速寿命试验台Fig.10 Bearing accelerated life test bed

表2 LDK UER204轴承参数Tab.2 LDK UER204 bearing parameters
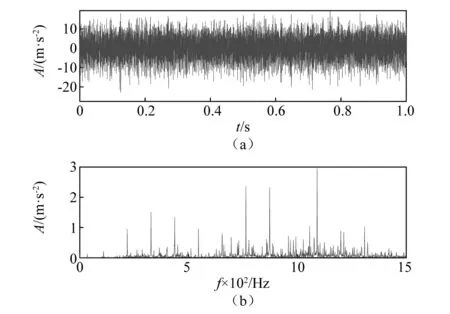
图11 XJTU-SY内外圈复合故障时域波形及其频谱Fig.11 Time domain waveform and spectrum of XJTU-SY composite fault
采用本文提出的方法对复合故障信号进一步分析,得到平均Infogram分析结果如图12(a)所示。从图12(a)可知,平均谱负熵最大的共振频带,确定带通滤波器的中心频率fc为1 600 Hz、带宽Bw为3 200 Hz。对信号进行带通滤波,滤波后信号时域波形及其包络谱如图12(b)所示。从图12(b)的包络谱中,仅能找到外圈故障的倍频(2~5fo,7~8fo),无法找到内圈相关频率。
进而采用参数优化CYCBD方法对故障进行分离。根据外圈理论故障频率设置循环频率集[107.91,215.82,…,1 079.10],以包络谱稀疏度为评价指标,经过两次筛选后,得到外圈滤波器长度优化结果,如图13所示。从图13(a)可以确定精细搜索的上限为700,从图13(b)可知,CYCBD最佳滤波器长度L应设置为700。经参数优化CYCBD处理后得到解卷积信号及其包络谱,如图14所示。从图14可知,包络谱中存在清晰的与外圈故障频率理论值近似的基频(109.4 Hz)及其倍频(2~9fo),不含其他故障成分,外圈故障信号被成功提取出来。
同样地,在提取内圈故障时,设置循环频率集为[172.09,344.18,…,1 720.9],滤波器长度优化结果如图15所示。从图15可知,CYCBD滤波器长度L应设置为740。得到解卷积信号及其包络谱如图16所示。

图12 平均Infogram及优选频带时频域波形Fig.12 Average Infogram and optimize frequency band time domain and frequency domain waveform
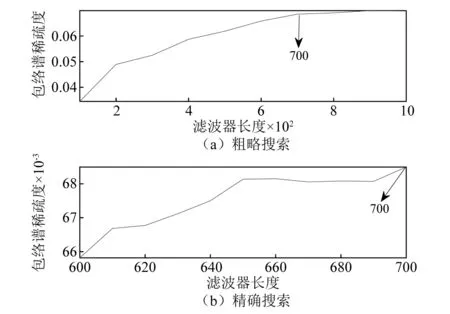
图13 外圈滤波器长度优化过程Fig.13 Filter length optimization process for outer ring fault

图14 外圈故障信号时域波形及包络谱Fig.14 Time domain waveform and envelope spectrum of outer ring fault signals
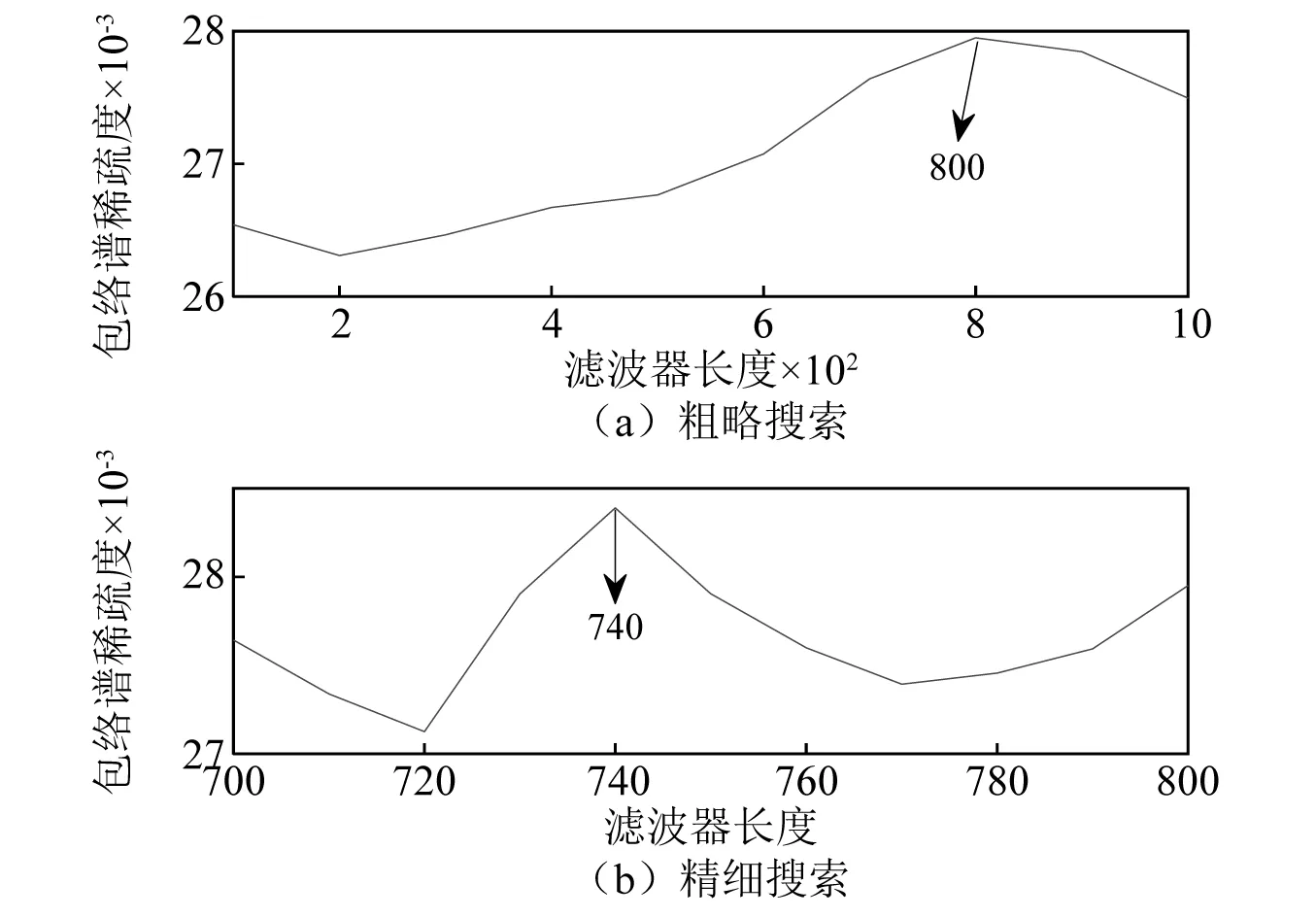
图15 内圈滤波器长度优化过程Fig.15 Filter length optimization process for outer ring fault

图16 内圈故障信号时域波形及包络谱Fig.16 Time domain waveform and envelope spectrum of inner ring fault signals
从图16可知,包络谱中包含清晰的与内圈故障理论值相近的基频(171.9 Hz)及其倍频(2~6fi,8fi),内圈故障信号被成功提取出来。综合以上特征,可以确定该轴承同时存在内圈和外圈故障。
4.2 自制试验平台实测信号论证与分析
本文使用自制试验平台完成滚动轴承内外圈复合故障试验,该平台由驱动电动机、转轴、液压油缸、测试轴承、传感器等部件组成,结构如图17所示。试验轴承为深沟球轴承,型号为6205-2RSH,结构参数如表3所示。为模拟复合故障,分别在测试轴承内圈和外圈设计了一个宽0.2 mm的裂缝,如图18所示。试验中转速fr为1 797 r/min,采样频率fs为25.6 kHz。试验数据每10 s采集一次,两组数据之间间隔5 s。由式(18)和式(19)计算得轴承内圈故障基频理论值fi=162.33 Hz,外圈故障基频理论值fo=107.22 Hz。
滚动轴承复合故障信号时域波形及频谱,如图19所示。从图19可知,时域波形具有明显的脉冲成分,且呈现周期性波动,但仅根据时域波形不能直接知晓滚动轴承的故障类型和故障位置,频谱中也未找到明显的故障频率。

图17 自制试验平台Fig.17 Self-made experimental platform

表3 测试轴承参数Tab.3 Test bearing parameters

图18 测试轴承Fig.18 Test bearing

图19 试验信号时域波形及其频谱Fig.19 Time domain waveform and spectrum of experimental signal
利用本文方法对复合故障信号进一步处理,平均Infogram如图20(a)所示。从图20(a)可知,带通滤波器fc应设置为2 266.67 Hz、Bw为2 133.33 Hz。滤波后信号时域波形及其包络谱如图20(b)所示。从图20(b)可知,包络谱中仅存在与理论值相近的内圈故障基频163.3 Hz、外圈故障基频108.6 Hz及其2倍频217.6 Hz,且故障特征频率交织在一起。

图20 平均Infogram及优选频带时频域波形Fig.20 Average Infogram and optimize frequency band time domain and frequency domain waveform
根据各理论故障特征频率,设定相应的循环频率集。依据包络谱稀疏度曲线选择CYCBD的最优滤波长度,优化结果如图21和图22所示。从图21、图22可知,提取外圈与内圈故障的最佳滤波器长度L分别为330及650。采用参数优化CYCBD提取到的外圈和内圈故障频率及其包络谱,如图23和图24所示。从图23、图24可知,分离效果与前两个案例一致,进一步论证了方法的有效性。

图21 外圈滤波器长度优化结果Fig.21 Filter length optimization process for outer ring fault
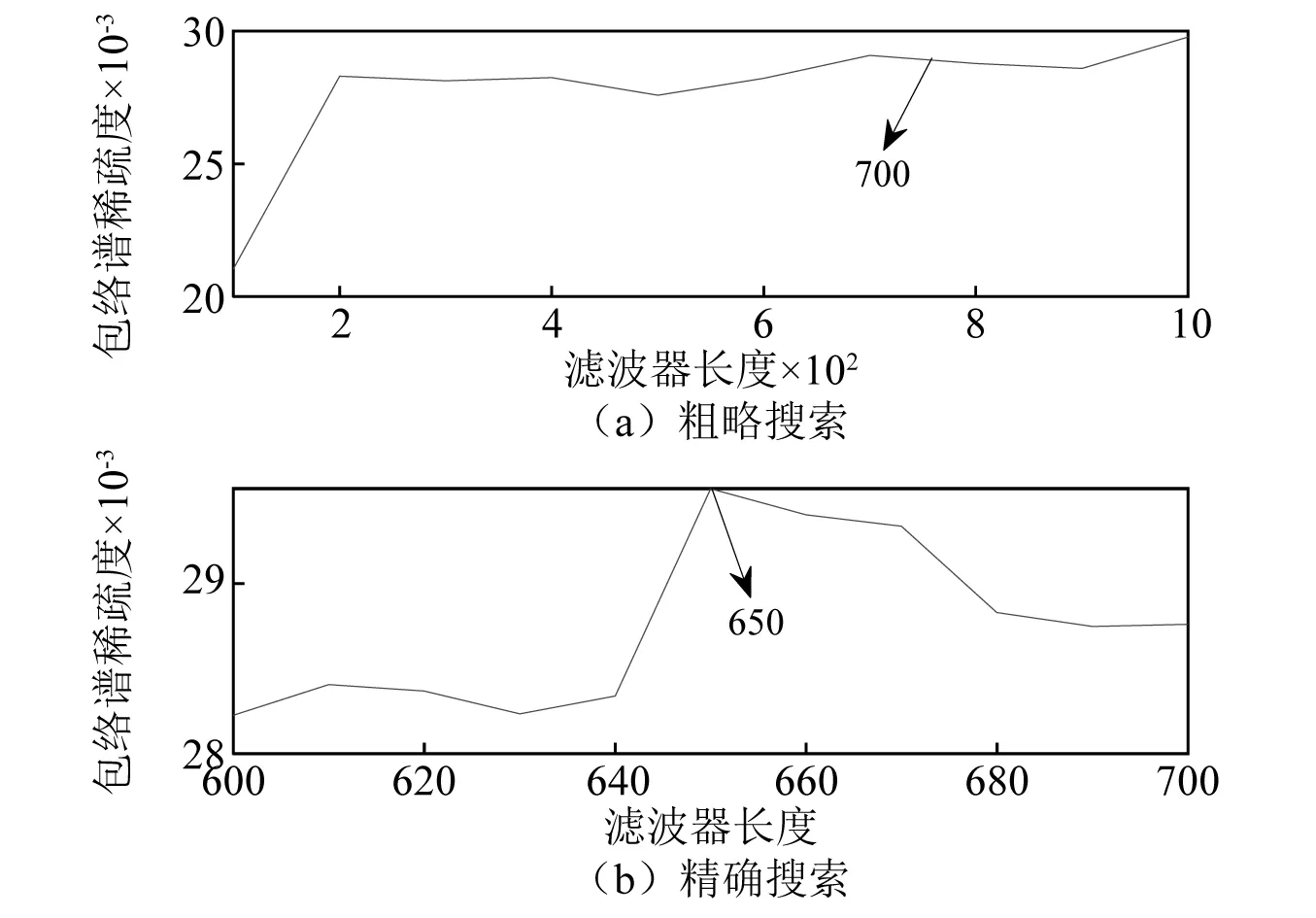
图22 内圈滤波器长度优化结果Fig.22 Filter length optimization process for inner ring fault

图23 外圈故障信号时域波形及包络谱Fig.23 Time domain waveform and envelope spectrum of outer ring fault signals

图24 内圈故障信号时域波形及包络谱Fig.24 Time domain waveform and envelope spectrum of inner ring fault signals
5 结 论
本文针对CYCBD中滤波器长度选择问题,提出了自适应的优化方法,并将Infogram与参数优化CYCBD相结合,应用于滚动轴承复合故障特征提取及分离中,通过对仿真信号及试验数据的分析,得出以下结论:
(1) 为消除噪声对复合故障信号的影响,利用Infogram方法的优势,有效确定带通滤波器参数,提取包含故障信息较多的频带,为故障进一步分离建立了基础。
(2) 针对CYCBD参数对解卷积效果与效率的影响问题,采用最大包络谱稀疏度选择最佳参数。并将参数优化CYCBD方法引入复合故障特征分离中,消除了信号之间的相互耦合,有效提取了各故障成分,实现故障信号的有效分离。
(3) 通过滚动轴承复合故障的仿真试验及实测信号分析,结合Infogram和参数优化CYCBD方法可以有效解决复合故障难以全面诊断的问题,实现了复合故障特征的准确分离和有效提取。
