求解一类代数Riccati 方程的Anderson加速算法

王小利，宋 岩，凌永辉

(闽南师范大学数学与统计学院，福建漳州 363000)

产生于运输问题的一类非对称代数Riccati 方程具有以下形式：

Juang[1]在1995 年证明了矩阵方程（1）正解的存在性，并在文献[2]中给出了一种近似计算最小正解的数值算法.考虑到实际应用及解的物理意义，最小正解的计算是研究者着重关注的问题.Lu[3]在2005 年证明了方程（1）的解满足以下形式：

其中◦表示Hadamard 乘积，n阶方阵T=(tij)= (1δ i+γj)，n维向量u和v满足

于是，求解矩阵方程（1）的最小正解等价于求解非线性向量方程（3）的最小正解.

近几年来，关于求解方程（3）最小正解已经取得了大量的成果.Lu[3]在2005 年提出一种不动点迭代（Fixed Point Iteration，FP）法来求解方程（3）的最小正解，随后又在文献[4]中进一步给出求解该方程的Newton 法.随后，Lin 等[5]改进文献[3]中的不动点算法得到一种收敛更快的不动点算法.在前人的基础上，Bai 等[6]在2008 年基于矩阵分块的Jacobi 迭代和Gauss-Seidel迭代给出了NBJ（Nonlinear Block Jacobi）法和NBGS（Nonlinear Block Gauss-Seidel）算法，这两种算法可用于计算接近奇异情况下的问题.随后，Lin[7]又对文献[6]中方法进行改进.同年，Lin 等[8]提出基于两步Newton 法的数值算法，并且证明了其单调收敛性.Ma 等[9]在2016 年提出了修正的Jacobi 型不动点迭代法和修正的Newton 型迭代法.Miyajima[10]在2017 年根据解的特殊结构提出一种适用于非奇异情况的直接求解算法.Zhang 等[11]在2020 年提出了带参数的Newton 外推法以及改进的倍增算法，并利用Cayley 变换给出了收敛性分析.其他方法详见文献[12-14]及其参考文献.

为改善不动点迭代在求解大规模方程接近奇异情况下收敛速度较慢的问题，本文考虑了一种新的不动点加速算法，这种加速方法最早是由Anderson[15]在1965 年提出的.Fang 等[16]在2009年提出了基于该加速方法的多割线迭代法，并将其应用于电子结构计算.Walker 等[17]在2011 年证明了在一定条件下，Anderson 加速与GMRES（Generalized Minimal Residual）是等价的，并讨论了几种算法的实施.Toth 等[18]在2015 年给出了Anderson 加速应用在线性及非线性问题上的收敛性分析.基于该加速框架，本文给出了求解方程（3）的一种不动点加速算法，并与FP、NBJ、NBGS 三种不动点迭代算法进行数值实验比较.非奇异情况下的数值结果显示，该加速算法较FP、NBJ、NBGS 法有较好的计算效能.在接近奇异情况下，较FP、NBJ、NBGS 三种算法均有良好的计算效能，特别是在计算接近奇异的大规模问题时，该加速算法优势尤为明显.

1 Anderson 加速算法

对于非线性方程（3），Lu[3]在2005 年给出了求解该方程的不动点迭代形式：

该算法计算简单，运算量只有 O(n2)，在非奇异情况下具有良好的计算效能.但在解决接近奇异的问题时，收敛速度缓慢.特别是，计算接近奇异的大规模问题时，需要花费很长时间.为了解决这一问题，我们利用Anderson 加速对不动点迭代法（4）进行改进.

下面给出Anderson 加速的一般算法.

算法1 Anderson 加速法.

算法1 实现的主要困难是通过求解带约束最小二乘问题（5）来确定参数根据Fang等[16]的推导，上述算法的带约束最小二乘问题可以改写为无约束问题：

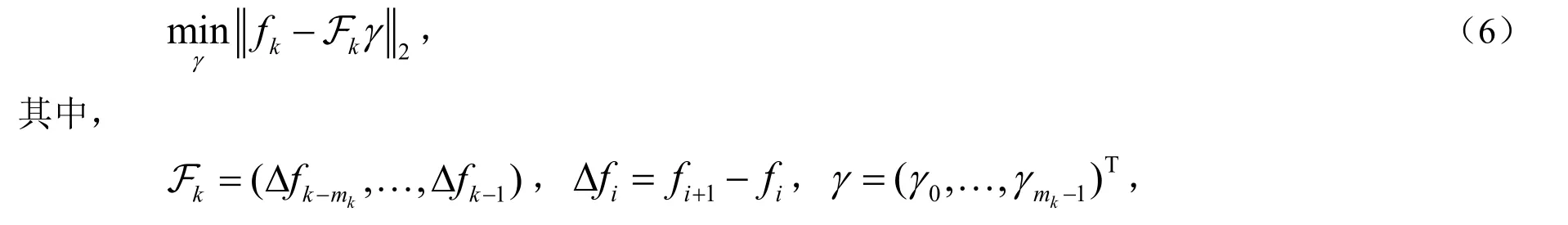
这里α与γ间的关系为

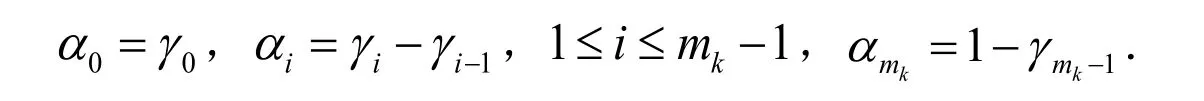
从而，算法1 中计算下一步迭代值的等式对应改写为：

2 最小二乘问题的求解

对于带约束最小二乘问题（5），Walker 等①Walker H,Ni P.A Linerly Consterained Least-Squares Problem in Electronic Structure Computations [C].International Conference on Computational &Experimental Engineering and Science,2010:43-49.在2010 年提出在一定条件下可以利用Lagrange乘数法直接求解.对于无约束的最小二乘问题（6），选用较为稳定的QR 分解进行计算.

这样求解无约束的最小二乘问题（6）可转化为求解一个mk×mk的上三角方程组.下面计算Fk的QR 分解.

下面给出Anderson 加速求解非对称代数Riccati 方程的算法描述.

3 数值实验

分别使用算法2（AA 算法）、不动点迭代[3]（FP 算法）、文献[6]所提出的非线性Jacobi 分块法（NBJ 算法）和非线性Guass-Seidel 分块法（NBGS 算法）来进行数值实验，比较这4 种算法在α、c的不同取值情形下的CPU 时间（单位为秒）、迭代次数IT 和相对残差ERR，其中CPU时间取算法计算十次的平均值.

将区间[0,1]进行划分，再利用四点的Guass-Legendre 求积公式求出每个子区间的节点ωi和权重ci，i=1,2,…,n，从而可以求出矩阵的P 和，其中维数n分别选512、1 024、2 048、4 096和8 192.

其中 eps ≈ 2.220 4 × 1 0−16.

所有实验均在CPU-3.60GHz（Intel(R) Core(TM) i7-4790），RAM-4GB 环境下进行，MATLAB版本为2013a.

在迭代终止条件相同的情况下，矩阵维数n固定为8 192 时，表1 为不同参数数值的实验结果.可以看出，在非奇异情况下，算法AA 与NBGS 计算效率相似，但随着参数的取值逐步接近奇异情况，算法AA 的优势也越来越明显.不管是CPU 时间、迭代次数还是残差，都明显优于其他三种算法.

表1 n= 8 192时不同参数的数值模拟

表2 为选定参数 (α,c)= (10−7,1 − 5 × 10−7)，矩阵维数n取不同值的实验结果.可以发现，该方法在计算接近奇异情况的大规模问题时，相较其他三种算法，算法AA 效果尤为显著，大大节省了计算成本.

表2 α= 10 −7 ,c=1 − 5×10−7时不同矩阵维数的数值模拟

表3 为(α,c)= (0.001,0.999)，矩阵维数n固定为4 096 时不同m的实验结果.

表3 α= 0.001,c= 0.999,n= 4 096时不同m 的数值模拟

表4 为α= 10−5，c=1 − 10−4，矩阵维数n为2 048 时不同m的实验结果.

表4 α= 10 −5 ,c=1 − 10−4,n= 2 048时不同m 的数值模拟

对比收敛较快的NBGS 法可以得出，选取适当的m，迭代次数与误差也会有所改变，选取最优的m可在一定程度上减少不必要的运算.当参数(α,c)接近奇异到一定程度时，即使不取最优的m，也有较好的收敛效果.这表明算法AA 对于求解方程（3）最小正解是十分有效的.

图1 为不同参数的收敛过程.图1（a）为取参数 (α,c) = (0 .01,0 .9 9)，m=12，矩阵维数n= 512时不同方法的数值实验结果；图1（b）为取参数 (α,c)=(1 0−6,1 −10−5)，m=7，矩阵维数n= 4 096时的实验结果.可以看出，随着参数的取值接近奇异情况，较其他三种方法，算法AA 具有良好的计算效能.

图1 不同参数的收敛过程