一种ICS异常检测的优化GAN模型

顾兆军，刘婷婷，2，隋 翯

(1.中国民航大学 信息安全测评中心，天津 300300；2.中国民航大学 计算机科学与技术学院，天津 300300；3.中国民航大学 航空工程学院，天津 300300)

工业控制系统(Industrial Control System，ICS)是国家关键基础设施的核心[1]，物理安全和网络安全是其平稳运行的必要条件[2]。然而随着工业控制系统逐渐接入互联网，其网络安全问题愈加凸显[3-4]。工业控制系统网络安全保障体系包括防护、检测、响应和恢复4个层面[5]，检测是其中重要环节，负责识别违反安全策略的行为或被攻击的迹象[6-7]，为告警和响应提供必要信息。

检测从技术角度可分为误用检测和异常检测[8]。异常检测由于对未知攻击的高效识别，受到研究人员的广泛关注，基于统计分析、基于数据挖掘、基于特征匹配和基于机器学习等方面的异常检测研究成果颇为丰富。近年，基于深度神经网络的异常检测技术逐渐成为研究热点[9-11]。自动编码器网络(AutoEncoder，AE)[12]、循环神经网络(Rerrent Neural Network，RNN)[13]、长短时记忆网络(Long-Short Term Memory，LSTM)[14]、卷积神经网络(Convolutional Neural Networks，CNN)[15]和深度自动编码高斯混合网络(Deep Autoencoding Gaussian Mixture Model，DAGMM)[16]等深度神经网络在应用中都取得了良好的效果。然而，工业控制系统的高实时性要求检测方法准确率更高，误报率更低；同时，工业控制系统中的类不平衡问题现象使分类器易于牺牲异常类来提高模型拟合能力，从而导致其准确率下降，泛化能力变差。

文献[17]提出的生成式对抗网络(Generative Adversarial Network，GAN)为工业控制系统异常检测提供了全新视角。该模型通过生成器与鉴别器博弈，使生成器能够不断学习从隐空间到真实数据的映射，从而使生成数据更符合真实数据分布。但是传统的生成式对抗网络模型无法处理高维特征的图像检测问题，因此文献[18]提出深度卷积生成式对抗网络(AnoGAN)，设计了从图像到隐空间映射的异常评分方法，实现了医疗图像异常识别，并成功分割出了图像中的异常区域。针对时间序列多元异常检测问题，文献[19]将GAN与LSTM-RNN相结合，提出了一种新的MAD-GAN模型。该模型同时考虑整个变量集特性以捕获变量之间的隐空间交互，在异常评分中也同时考虑鉴别损失和重构损失，在多个数据集上的实验结果表明该模型不仅具有优异的检测性能，在维数缩减、迭代稳定性等方面也具有独特优势。文献[20]的实验研究也得到了类似的结论。然而，上述模型均为基于“单向”生成式对抗网络模型的异常检测方法，生成器需要学习真实数据对应的隐空间特征，即其先验分布，从而导致检测算法的时间复杂度很高，计算成本偏大。

为了提高隐空间特征的学习效果和学习效率，文献[21]通过引入编码器设计了双向生成式对抗网络(BiGAN)，使模型具备学习真实数据到隐空间逆映射功能，为数据添加了隐空间特征“标签”，从而使模型具备了分类能力，尤其是在图像分类和识别方面具有突出优势。以双向生成式对抗网络模型为基础，结合网络入侵行为特征，文献[22]率先提出高效异常检测生成式对抗网络方法(EGBAD)，并实验证明了该方法不仅适用于图像数据，在网络入侵数据检测中，尤其在时间复杂度方面具有优异性能。进一步针对入侵检测中的离散数据，文献[23]在BiGAN基础上采用Dropout全连接网络，并使用Wasserstein距离替代了交叉熵和JS散度，并提出一种由剩余损失加权求和计算鉴别损失的模型，使检测准确率、召回率和F1得分都得到明显提升。BiGAN模型虽然通过引入编码器提高了真实数据得到对应的隐空间特征映射的学习能力，但处理数据类不平衡数据时，模型容易陷入局部最优。

因此，文献[24]提出了一种采用“编码-解码-编码”三层子网结构作为生成器的生成式对抗网络模型——GANomaly。该模型通过使原始数据和二次编码后数据的隐空间向量之间距离最小化，来学习正常数据分布；并通过被检测数据与该分布之间的距离评断是否异常，从而进一步提升了算法的学习能力。基于GANomaly思想，针对类不平衡数据，文献[25]提出异常分数由表观损失和潜在损失共同构成，并利用该方法通过对滚动轴承基准数据分析，实现了对物理机构的故障诊断。

上述已有研究成果充分说明基于生成式对抗网络的异常检测模型在处理类不平衡数据时具有独特优势。笔者提出了一种用于工业控制系统异常检测的隐空间特征重构生成式对抗网络模型——Latent Feature Reconstruction GAN(LFR-GAN)。在训练阶段，通过引入新的编码器，学习生成数据到隐空间的映射，实现生成数据的隐空间特征重构，并嵌入SE Block(Sequeze and Excitation Block)模块[26]提升有效特征权重，提高隐空间特征重构能力；鉴别器则同时鉴别两个编码器和一个生成器产生的3个数据对，加快模型收敛，提高模型精度和泛化能力。在检测阶段，综合考虑重构和鉴别损失，借鉴WGAN-GP[27]研究思路，采用L2范数优化异常评分公式，克服模式崩塌[28]问题。最后，在公开数据集SWaT[29]和WADI[30]上对LFR-GAN模型进行了验证，并与AnoGAN、BiGAN和WGAN-GP等方法进行了对比。结果表明，从学习能力、检测能力、稳定性等方面，LFR-GAN模型都具有明显的优势。

1 LFR-GAN模型

模型分为训练和检测两个阶段。在训练阶段，模型通过编码器E1、E2和生成器G与鉴别器D不断对抗，学习正常样本的数据分布和隐空间特征。模型训练完成之后，基于训练模型对未知状态的测试样本进行异常检测。通过特殊设计的异常评分公式，计算待测数据样本的异常得分并排序，根据经验比例筛选出异常数据，从而判断待测数据是否异常。模型算法流程如图1所示。

图1 LFR-GAN异常检测模型算法流程

1.1 训练阶段

训练阶段如图2所示，数据空间输入样本x经过编码器E1编码，得到其在隐空间的特征E1(x)；同时隐空间随机噪声z经过生成器G解码，在数据空间得到生成样本G(z)；然后生成样本G(z)进一步经过编码器E2编码，得到生成数据在隐空间的重构特征E2(G(z))。从而，得到了3对由数据空间样本和其隐空间特征组成的数据对——(x，E1(x))，(G(z)，z)和(G(z)，E2(G(z)))。鉴别器D通过鉴别这3个数据对得到鉴别损失，并根据鉴别损失逐步递归求解模型梯度，实现权重更新，反向优化编码器E1、E2和生成器G。

训练过程中，对于生成器，其使生成样本G(z)尽可能接近真实样本x；对于编码器E2，其使重构的隐空间特征E2(G(z))尽可能接近于真实样本对应的隐空间特征E1(x)；编码器E1、E2以及生成器G通过与鉴别器D不断对抗博弈实现迭代优化，以使鉴别器越来越难以分辨这3个数据对的来源，使得生成数据趋近于真实数据，隐空间的重构特征趋近于真实数据映射到隐空间的特征。

对于鉴别器，其目标是准确分辨出3个数据对的来源，并给出数据对来自于生成数据的可能性。当数据对来自真实数据(x，E1(x))时，鉴别器给出的数据对来自于生成数据可能性判据D(x，E1(x))应趋向于0，当数据对来自生成器(G(z)，z)或(G(z)，E2(G(z)))时，鉴别器给出的数据对来自于生成数据可能性判据D(G(z)，z)和D(G(z)，E2(G(z)))应趋向于1。

通过以上分析，该模型的训练目标是实现一个最大最小二元博弈平衡：

(1)

而V(D，E1，E2，G)可表示为

V(D，E1，E2，G)=Ex～pX[Ez～pE1(·|x)‖D(x，z)‖w]+Ez～pZ[Ex～pG(·|z)‖1-D(x，z)‖w]+

(2)

图2 LFR-GAN模型训练过程示意图

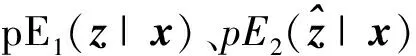
在训练过程中，可以通过计算KID值[31](Kernel-Inception Distance)来评估模型学习训练样本分布的情况。KID值是真实样本和生成样本概率分布之间的差异，计算公式如下：

DKID=MMD(Pr，Pg) ，

(3)

其中，Pr为真实样本的分布，Pg为生成样本的分布，MMD(Pr，Pg)可表示为

(4)

(5)

其中，d为训练集维数。

按式(3)～(5)可以计算隐空间特征z分布和真实数据编码得到的隐空间特征E1(x)分布之间的KID值。KID值可以反映模型学习能力，KID值越小，表示两个分布之间的差异越小，模型的学习能力越强。

1.2 检测阶段

模型训练完成之后，将已训练好的编码器、生成器和鉴别器重组构成检测模型，如图3(a)所示。根据检测模型产生的损失，使用异常评分公式来计算检测数据的异常得分S：

S=λLG+(1-λ)LD，

(6)

其中，λ是一个常量，根据经验取0.2；LG为重构损失，用来衡量测试样本和生成样本的差异；LD为鉴别损失，用来衡量(x，E1(x))和(G(E1(x))，E2(G(E1(x))))两个数据对特征匹配损失，以评估生成数据是否和真实数据有相同的特征。

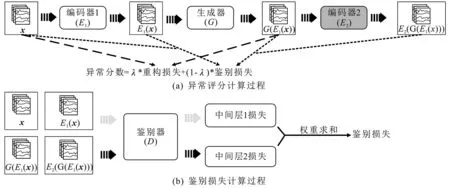
图3 LFR-GAN模型检测过程示意图

LG和LD的计算公式如下：

LG=‖x-G(E1(x))‖2，

(7)

LD=‖fD(x，E1(x))-fD(G(E1(x))，E2(G(E1(x)))‖2。

(8)

式(7)中的x为测试数据，E1(x)表示该数据编码后的隐空间特征，G(E1(x))表示将编码器E1生成的隐空间特征解码后的生成数据。式(8)中fD为嵌入鉴别器中的中间层，如图3(b)所示，fD(·)为该中间层的输出。L2范数对异常值更加敏感，更有利于得到稳定解，因此采用L2范数对LG和LD两个损失函数进行计算。通过以上计算，测试数据的异常评分越高，越有可能为异常。在计算出所有样本的异常分数后，将数据按异常分数降序排列，根据经验预先设置异常比例，将异常分数处于该比例范围内的样本标记为异常。

2 实验与结果

2.1 实验设置

实验采用SWaT和WADI两个公开数据集，SWaT(the Secure Water Treatment)是一个水处理操作实验系统，数据集采集了11天实验数据，其中最后4天里共发动36次攻击。WADI(WAter DIstribution)是一个分布式跨区域水务管道系统，连续16天采集了系统的网络流量、传感器和执行器数据，其中只有2天具有攻击数据，二者均是典型的类不平衡数据集。本实验将两个数据集均分成训练集和测试集。两个训练集中所有数据均为正常样本。两个测试集异常样本占比分别约为11.98%和5.99%，数据集详细信息如表1所示。

表1 SWaT和WADI数据集情况

实验使用Intel 酷睿i7 9750H处理器和NVDIA GeForce GTX 1650显卡，于Tensor Flow 1.14.0架构在Python 3.6下实现。实验采用Adam优化器，学习率r=0.000 01，隐空间向量维度设为256，隐藏层维度设为128，训练轮数根据经验设置为60。

2.2 实验结果和分析

首先，根据式(3)～(5)计算LFR-GAN模型在SWaT和WADI两个数据集上的KID值随迭代次数变化，来检验模型在训练阶段的学习能力，并与AnoGAN，WGAN-GP和BiGAN进行对比，结果如图4所示。

由图4可知，随着迭代次数增加，LFR-GAN模型KID值基本处于0.1以下，明显低于AnoGAN和WGAN-GP，与BiGAN相比也可以得到更低值，表明LFR-GAN模型得到的隐空间特征z分布和真实数据编码得到的隐空间特征E1(x)分布间差异更小，模型的学习能力更强。在WADI数据集的初始学习阶段，LFR-GAN模型KID值出现一些偏大值，是由于LFR-GAN模型在学习高维数据时尚未达到最优结果；随着迭代次数增加，LFR-GAN模型KID值逐渐回落到低值稳定状态，模型表现出明显的学习能力优势。

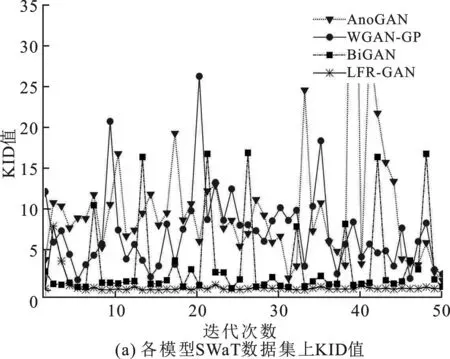
此外，随迭代次数增加，除在WADI数据集的初始学习阶段出现一些波动外，LFR-GAN模型KID值基本处于稳定状态，而AnoGAN，WGAN-GP和BiGAN均出现较大幅度的波动且在实验参数范围内未见收敛趋势。说明与上述3个模型相比，具有SE Block的LFR-GAN模型有更好的学习稳定性，可以在更少的迭代次数下达到最佳学习状态。

工业控制系统异常检测注重检测效率，异常的出现往往会造成巨大的损失，所以在检测阶段更关注召回率，并兼顾准确率、精确率和F1得分。实验使用召回率、精确率和准确率来反映模型的检测性能，F1得分作为召回率和精确率的调和平均，检测结果如图5所示。

由图5可知，LFR-GAN模型在SWaT数据集上的召回率为0.971 7，在WADI数据集上的召回率为0.996 3，相比其他模型，LFR-GAN模型的召回率大概可以提高2%～8%。召回率提高意味着异常数据误报率降低，LFR-GAN既可以更准确地识别异常样本，提高系统的安全性，又可以兼顾系统的实时性，避免由于误报率过高导致的系统无效响应。实验结果表明，基于隐空间特征重构的LFR-GAN针对不平衡数据集，相比其他模型具有更好的检测性能。

此外，LFR-GAN模型的准确率和精确率均高于其他模型，在SWaT数据集上的准确率为0.933 7，精确率为0.952 3；在WADI数据集上的准确率为0.970 6，精确率为0.976 9。相比其他模型，准确率提高了约5%～11%，精确率提高了约2%～7%。精确率提高意味着漏报率降低，LFR-GAN可以更好地预测异常数据。上述表明LFR-GAN无需使用异常样本进行训练，也可实现高准确率和高精确率。并且LFR-GAN模型的F1得分也高于其他模型，在SWaT数据集上的F1得分为0.956 4；在WADI数据集上的F1得分为0.971 5，相比其他模型，F1得分大概提高了3%～8%。F1得分作为模型的综合评价指标，它同时考虑精确率和召回率，让两者达到一个平衡点。所以F1分数在一定程度上反映了模型的综合性能和稳定性，F1值越大，模型综合性能和稳定性越好，进一步说明了LFR-GAN模型的优势。

由于精确率-召回率曲线(Precision-Recall Curve，PR曲线)对样本比例敏感，本实验还使用PR曲线来衡量模型在类不平衡情况下的异常检测性能，结果如图6所示。

PR曲线可以用来对比分类器间的性能优劣。由图6可知，LFR-GAN在两个数据集上的PR曲线均可包围其他三个模型的PR曲线，曲线与坐标轴围成的面积最大。因此，LFR-GAN模型的分类性能最优，BiGAN较好，WGAN-GP中等，AnoGAN性能最差。可见，在类不平衡情况下，LFR-GAN模型的PR曲线更饱满，对应的曲线下面积更大，分类性能更好，与图5结果相一致。

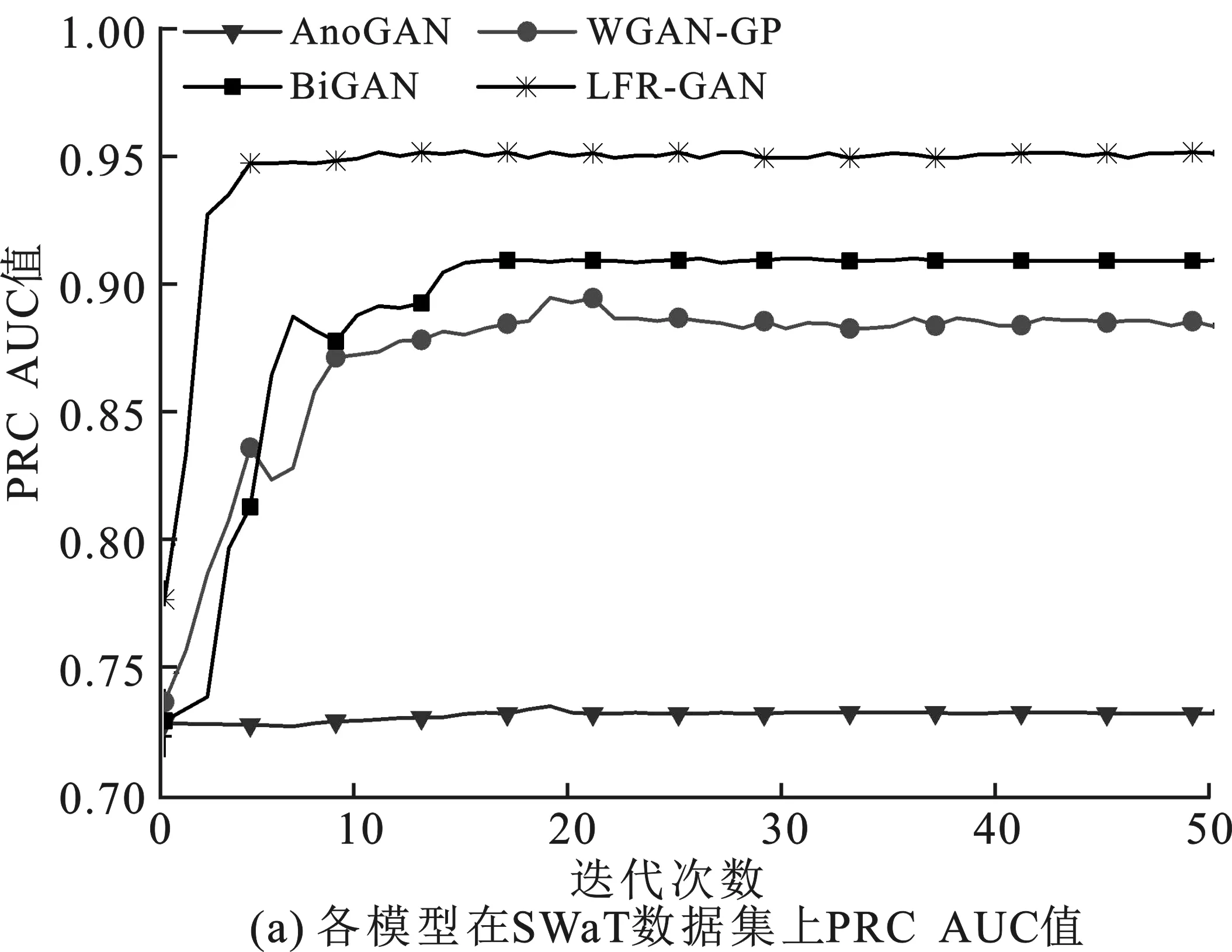
实验通过每次迭代得到的PRC AUC(Area Under Curve)值来反映模型在检测阶段的运行稳定情况。PRC AUC值即为PR曲线下面积，它能够说明模型在验证阶段的性能，面积越大，表示分类器的性能越好。在模型每次迭代后进入检测阶段，得到PRC AUC值并与AnoGAN、WGAN-GP和BiGAN进行对比，结果如图7所示。

由图7可知，从第一次迭代开始，LFR-GAN的运行数值一直高于其他模型，并处于上升的阶段。模型趋于稳定后，在WADI数据集上，LFR-GAN的PRC AUC值最优时接近1。上述结果说明，模型趋于稳定后，LFR-GAN模型运行的情况最好。此外，随迭代次数增加，LFR-GAN模型基本在10次迭代内PRC AUC值达到最大，且运行平稳，而AnoGAN的值最低，WGAN-GP和BiGAN模型需迭代15～30次后才能达到稳定。实验证明了子网结构采用卷积神经网络的LFR-GAN能更好地提取样本的局部特征，且具有隐空间特征重构的模型可用更少的迭代次数完成学习，达到最优状态，模型具有更好的运行稳定性。

为了更直观地展示各模型异常检测的效果，实验分别在SWaT和WADI测试集随机选取1 000个样本点，根据设定的异常评分公式(式(6))计算每个样本的异常评分，检验模型的分类能力，并与AnoGAN、WGAN-GP和BiGAN进行对比，结果如图8和图9所示。

LFR-GAN相比其他模型能更好地区分异常样本，而AnoGAN和WGAN-GP均存在漏报的现象，BiGAN相对漏报率低，但没有一个清晰的分类边界。可见与其他模型相比，LFR-GAN特殊设计的异常评分公式，能够更有效划分正负样本的界限。

3 结束语

笔者针对工业控制系统异常检测工作中类不平衡问题，根据生成式对抗网络架构，新增生成数据向其隐空间映射的编码器，引入SE Block模块，采用L2范数优化异常评分公式，提出了LFR-GAN异常检测模型，并在SWaT和WADI数据集上进行了性能验证。

与AnoGAN，WGAN-GP和BiGAN的对比表明，LFR-GAN模型在处理类不平衡问题时，训练过程全部使用正常样本，但却可以获得更好的学习性能、检测结果和模型稳定性。可见LFR-GAN模型鲁棒性更强，稳定性更好，具有很好的现实可用性和有效性。随着检测技术和设备性能不断提升，计算能力和存储能力不断增强，LFR-GAN模型在ICS异常检测中将更具有前景。