船闸浮式系船柱受荷响应力学模型

刘明维，李明龙，吴林键，江 涛，赵殿鹏

(1. 重庆交通大学 国家内河航道整治工程技术研究中心，重庆 400074； 2. 长江三峡通航管理局，湖北 宜昌 443002； 3. 浙江省交通工程管理中心，浙江 杭州 311215)

0 引 言

随着三峡库区建成蓄水，长江中上游的通航条件得到了显著改善。三峡船闸通航船舶货运总量2011年已经突破1亿吨，2019年达到1.44亿吨[1]。目前，通航船舶在闸室内停靠主要依赖于浮式系船柱，该通航设施在浮力的作用下随水位变化而上下浮动，进而满足通航船舶安全系缆的要求。然而在实际使用过程中，受通航船舶大型化、系缆不规范、船舶进闸速度过快、浮式系船柱被漂浮物卡住以及船闸灌泄水作用等因素影响，浮式系船柱所受系缆力易超出其设计允许值，导致其结构发生破坏，进而造成吊船、拉船入水、船体损伤甚至船员伤亡等重大安全事故[2-7]。因此，如何实现对船闸浮式系船柱系缆安全的快速评估，具有重要的现实意义。

目前，船闸浮式系船柱结构主要通过安装在通航船舶缆绳上的缆绳载荷监测系统进行系缆安全评估。然而，船闸浮式系船柱结构的实际受力不仅与船舶系缆力大小有关，还受缆绳系缆角度、系缆方向、系缆位置等多因素共同影响[8-9]。仅通过监测缆绳上的系缆力大小无法有效地反映船舶系缆力对船闸浮式系船柱结构本身受力特性的影响，难以准确地评估船舶过闸通航的系缆安全状态，具有较大的局限性。同时，这种船闸浮式系船柱系缆安全评估方法对于通航枢纽管理单位来说不具有主动性，无法实时全覆盖跟踪监测所有的通航船舶进而进行安全预警。

船闸浮式系船柱结构的应变能够直接反映其受力状态。近年来有学者提出通过监测系船柱表面应变，进而实现对系船柱结构的系缆安全评估[10,12]。实际情况中，在同样大小的系缆力下，不同的系泊高度、系缆角度对船闸浮式系船柱的作用并不相同，仅通过简单测量几点船闸浮式系船柱结构上面的应变，并以此作为评估浮式系船柱系缆安全的依据，该方式的合理性尚需进一步探讨[12]。

为保障船闸浮式系船柱在运行状态下的系缆安全，结合某大型船闸工程项目中浮式系船柱的结构特点，采用理论推导与数值仿真技术相结合的方法对船闸浮式系船柱上部结构的受力状态进行分析，建立浮式系船柱受荷响应力学模型。通过选取船闸浮式系船柱柱身同一截面指定位置的应变，计算船舶系缆力大小，并将其与船闸浮式系船柱的系缆力设计允许值进行对比，可实现对船闸浮式系船柱系缆安全的快速评估。

1 船舶系缆力-浮式系船柱柱身应变特性关系

船闸浮式系船柱一般由浮筒、滚动装置、系船架三部分组成[13]。根据某船闸工程中浮式系船柱结构受力特点，将船闸浮式系船柱上部结构概化为简支外伸梁，即：将船闸浮式系船柱的空心圆柱体系船柱柱身概化为等截面弹性梁，并将用于固定该空心圆柱体的3块钢板概化为2个固定铰支座。系缆力合力F与水平面夹角为β(竖向角)，船闸浮式系船柱结构在系缆力作用下产生拉弯组合变形，见图1。

对于船闸浮式系船柱上任一受力点D，其应变主要包括轴向拉伸应变与弯曲应变两部分。

1.1 轴向拉伸应变

船闸浮式系船柱由线弹性材料构成，符合胡克定律。系缆力轴向分力Fz产生轴向拉伸，即：

(1)

推导可得：

(2)

式中:ε1为船闸浮式系船柱表面的拉伸应变；Fz为系缆力的竖向分力；σ为船闸浮式系船柱表面的拉伸应力；S为船闸浮式系船柱截面面积；E为船闸浮式系船柱弹性模量；a为待定系数。

1.2 弯曲应变

在弯矩作用下，船闸浮式系船柱结构产生弯曲应变。截面弯矩M包括Fxy产生的弯矩Mxy和Fz产生的弯矩Mz。

对于Fxy产生的弯矩Mxy：

Mxy=bFxy·(L1-h)·L2/L1

(3)

式中:L1为船闸浮式系船柱简支段长度；L2为船闸浮式系船柱悬臂段长度；h为应变测量点到船闸浮式系船柱上简支点距离；b为待定系数。

对于Fz产生的弯矩Mz，由于系缆力作用于一定宽度的半圆截面，所以：

cFz·(2R/π)

(4)

式中:R为船闸浮式系船柱轴向截面圆环半径；ω为船闸浮式系船柱圆柱体受力面任意一点与圆心连线和中性轴的夹角，见图2(a)；c为待定系数。

在纯弯曲下，推导可得船闸浮式系船柱截面D点弯曲应变，如式(5)：

(5)

式中：ε2为船闸浮式系船柱表面的弯曲应变；I为船闸浮式系船柱截面圆环的惯性矩；d为应变测量点到中性轴的垂直距离。

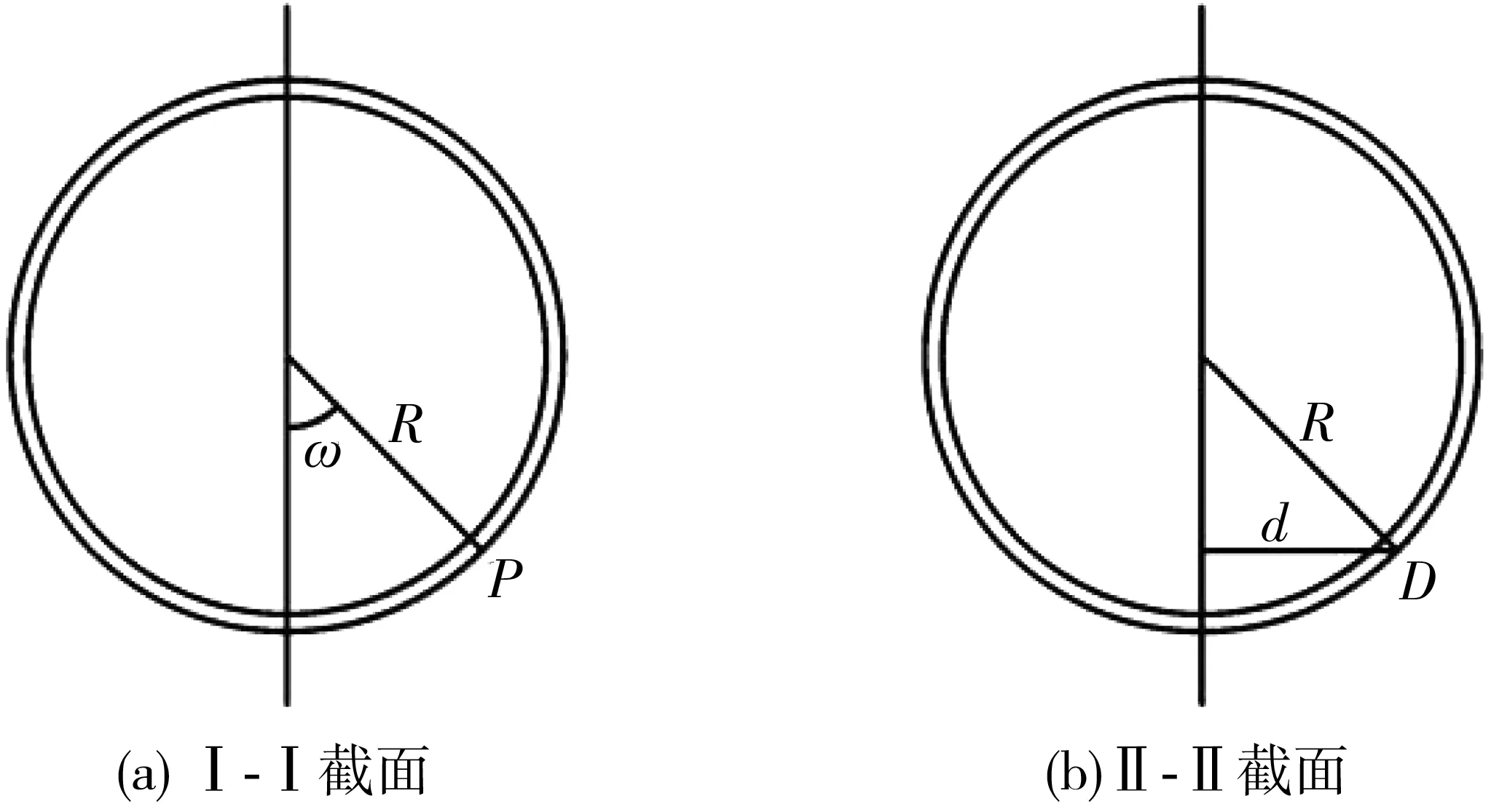
图2 船闸浮式系船柱Fig. 2 Floating bollard of ship lock

由应变叠加可得船闸浮式系船柱表面D点应变，如式(6)：

(6)

2 浮式系船柱受荷响应力学模型

2.1 模型的建立

在指定高度的系缆力作用下，船舶缆绳系缆点与测点截面间的距离为L2+h，缆绳与水平面夹角为β(竖向角)，有：

Fxy=Fcosβ

(7)

Fz=Fsinβ

(8)

在船闸浮式系船柱测点轴向截面表面选取3个应变测量点B、C、D，位置见图3，此时取h=600 mm。应变测量点B、C、D与中性轴的距离为：

dB=Rsinξ

(9)

dC=sin(ξ+μ)

(10)

dD=Rsin(ξ+μ+φ)

(11)

式中：ξ为连接测点和圆心的直线与中性轴的夹角；μ为B和C两测点与圆心连线的夹角，取10°；φ为C和D两测点与圆心连线的夹角，取10°，见图3。

测点B和圆心连线与闸墙线间的夹角为θ，取80°，则：

α=90°+ξ-θ

(12)

式中：α为缆绳与闸墙线的夹角(水平角)。

图3 船闸浮式系船柱应变监测位置及相关角度Fig. 3 Strain monitoring position and relative angle of floating bollard of ship lock

设应变监测点的应变为ξi，i代表B、C、D点，则B、C、D点的应变分别为εB、εC、εD，联列式(6)～式(12)，得：

(13)

式中：dB=Rsin(α+θ-90°)；dC=Rsin(α+θ+μ-90°)；dD=Rsin(α+θ+μ+φ-90°)。

基于式(13)即可求得船舶系泊缆绳与闸墙线的水平夹角α、缆绳与水平面的竖向夹角β和指定高度的系缆力F。

2.2 模型参数确定

为确定浮式系船柱受荷响应力学模型中的各待定参数，笔者拟采用浮式系船柱受荷仿真数值试验的方法对模型中各待定参数进行确定。

2.2.1 浮式系船柱受荷仿真数值试验

根据某船闸浮式系船柱各部件的实际尺寸，采用ANSYS Workbench建立浮式系船柱上部结构的三维数值模型[14]，见图4。

浮式系船柱上部结构各部件主要包含3种材料。其中，空心圆柱体系船柱柱身采用铸钢(ZG310-570)材料，平行于图4(b)XOY平面的3块板采用不锈钢(1CR18Ni9Ti)材料，其余部件均采用Q235型钢材。上述3种材料的弹性模量分别为200、193、200 GPa；密度分别为7 850、7 750、7 850 kg/m3；泊松比分别为0.30、0.31和0.30；屈服强度分别为310、207、250 MPa；抗拉强度分别为570、586、460 MPa。

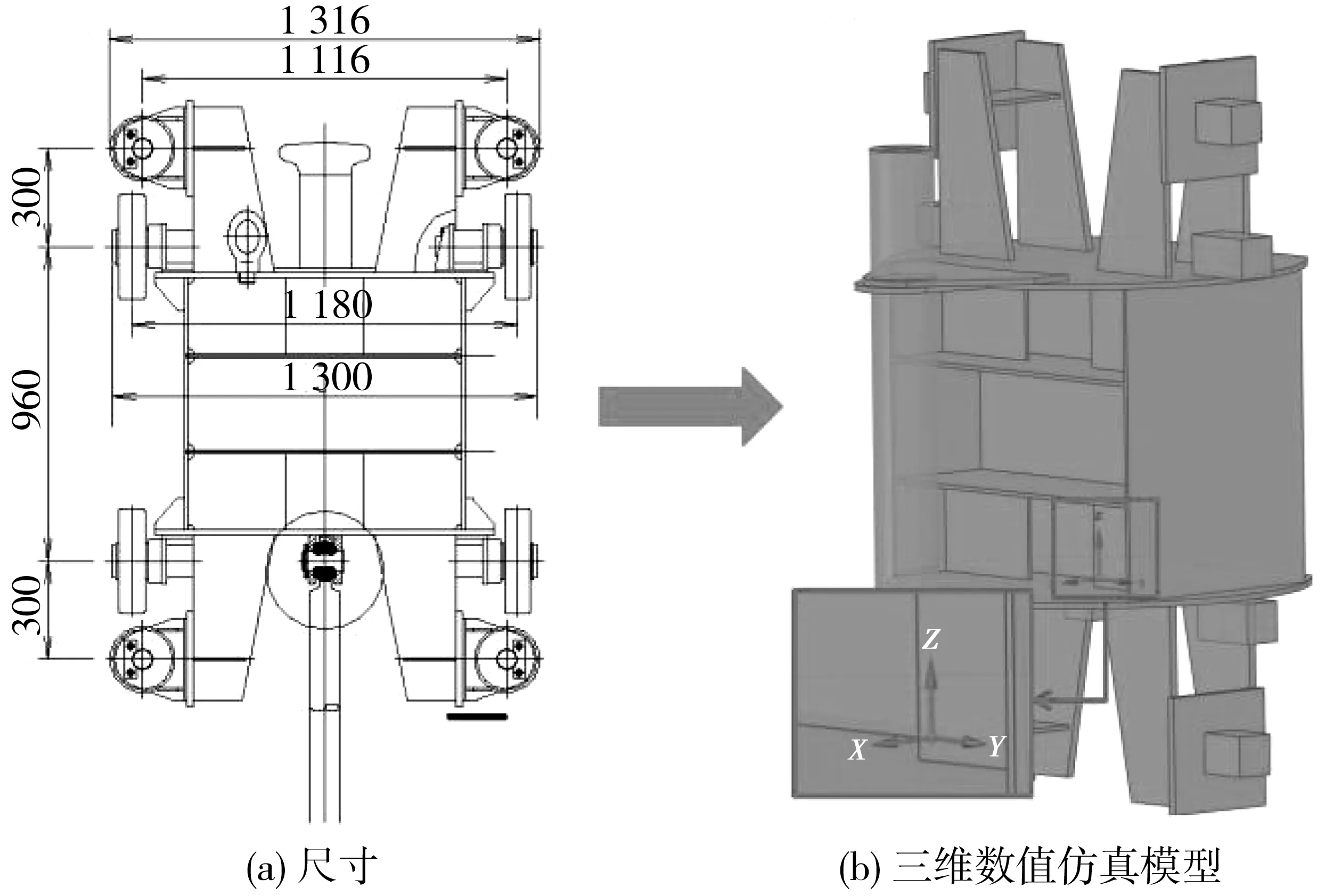
图4 船闸浮式系船柱Fig. 4 Floating bollard of ship lock

2.2.2 数值试验的计算工况

在数值仿真计算过程中，船闸浮式系船柱上部结构所受永久荷载考虑如下：①结构自重G=8.155 4 kN，方向竖直向下；②水的浮力与结构自重大小相等，方向相反。

综合考虑缆绳与闸墙线的水平夹角α、缆绳与水平面的竖向夹角β以及船闸浮式系船柱的对称性，船闸浮式系船柱数值仿真计算的可变荷载工况共设置3个因素(船舶系缆力F、水平角度α、竖向角度β)，每个因素分别设置5个水平，即：系缆力F分别取50、100、200、300、400 kN，水平角度α分别取30°、45°、60°、75°、90°，竖向角度β分别取0°、15°、22.5°、30°、45°。将每个因素的每个水平相互搭配进行全面计算，总计算工况为53=125次。

2.2.3 数值试验的计算结果

通过船闸浮式系船柱数值仿真模型计算，可分别得到在125种工况条件下，船闸浮式系船柱柱身各测点位置处的应变，见图5。

图5 数值仿真试验应变计算结果Fig. 5 Strain calculation results of numerical simulation test

2.2.4 模型参数确定结果

基于船闸浮式系船柱数值仿真试验的计算结果，选择各测点位置的相关参数，利用最小二乘法基本原理，对式(13)进行多元线性回归分析，可得到式(13)中的待定参数，见表1。

表1 船闸浮式系船柱受荷响应力学模型相关参数Table 1 Relevant parameters of load-bearing response mechanical model of floating bollard of ship lock

3 模型的验证与应用

为验证船闸浮式系船柱受荷响应力学模型的可靠性，选择与船闸浮式系船柱受荷响应力学模型参数确定所取可变荷载工况不同的其他可变荷载工况的结果进行对比分析，验证工况见表2。

表2 可靠性验证荷载工况Table 2 Reliability verification of load conditions

将B、C、D测点应变代入式(13)，计算出缆绳与闸墙线的水平夹角α′、缆绳与水平面的竖向夹角β′和指定高度的系缆力F′，见图6。

图6 可靠性验证荷载工况条件下的计算结果对比Fig. 6 Comparison of calculation results under load conditions of reliability verification

根据图6可计算得到船闸浮式系船柱受荷响应力学模型的误差，见图7。

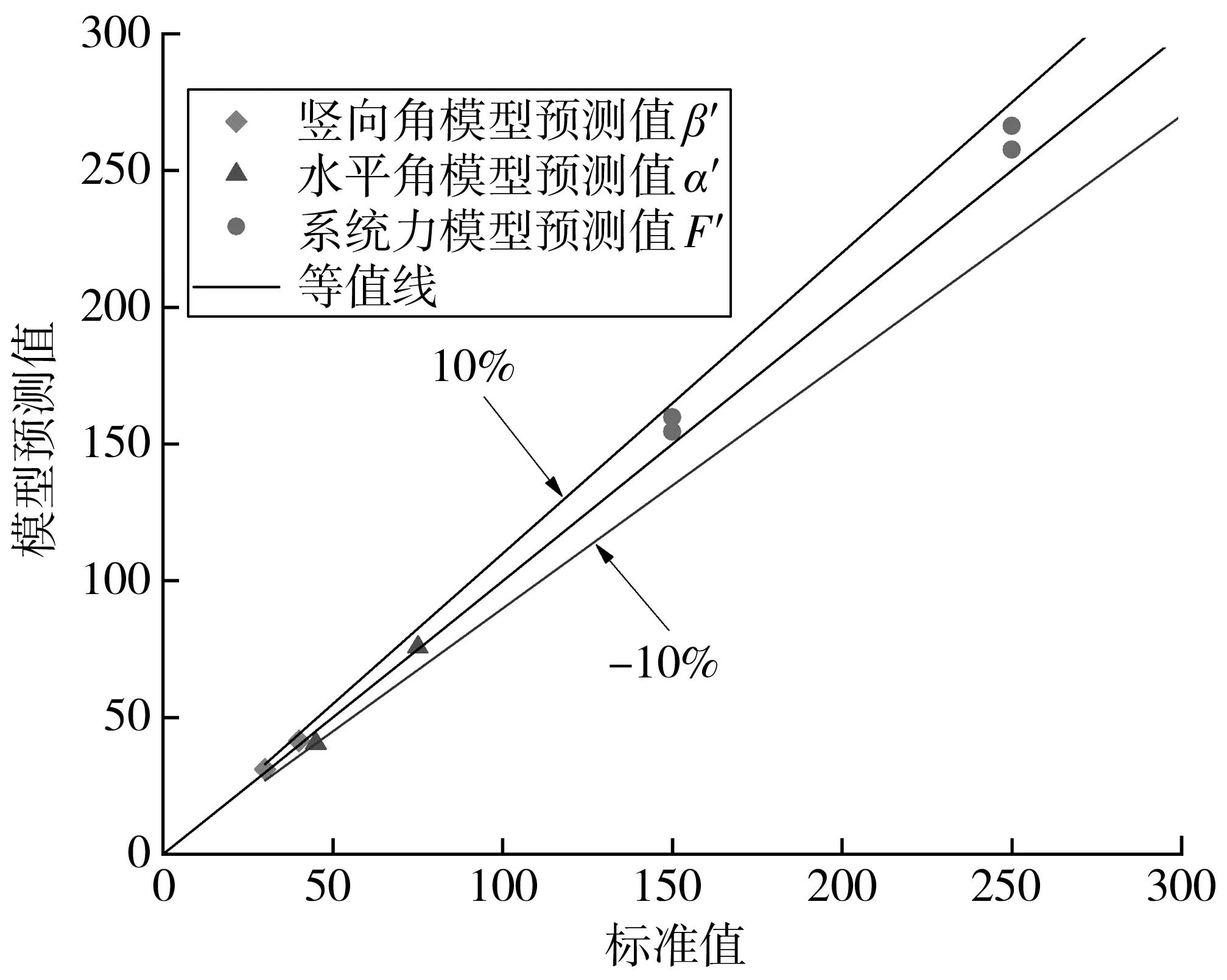
图7 船闸浮式系船柱力学模型反演误差Fig. 7 Inversion error of mechanical model of floating bollard of ship lock

由图7可知，船闸浮式系船柱指定高度的系缆力计算结果与数值仿真计算结果之间的最大误差为6.51%；缆绳与闸墙线的水平夹角α计算结果与数值仿真计算结果之间的最大误差为-9.74%；缆绳与水平面的竖向夹角β计算结果与数值仿真计算结果之间的最大误差为3.54%。由于数值仿真模型计算结果与实际测量结果之间存在误差，考虑实际使用情况，验证了文中模型的精度。

4 结 论

1)建立了反映船舶缆绳系缆力与船闸浮式系船柱柱身应变二者特性关系的船闸浮式系船柱受荷响应力学模型。通过测量船闸浮式系船柱柱身同一截面上指定测点的应变可以计算得到浮式系船柱所受系缆力的大小和方向，为实现船闸浮式系船柱在服役状态下的自动化感知与预警技术奠定了理论基础。

2)在船闸浮式系船柱的使用过程中，将计算得到的船舶系缆力与船闸浮式系船柱的系缆力设计允许值进行对比，可以实现对船闸浮式系船柱的系缆安全评估。

3)笔者提出的系缆安全评估方法，通过计算船闸浮式系船柱所受系缆力大小，解决了现有的系缆安全评估方法不能有效地评估船舶过闸通航安全状态以及不能全覆盖监测过闸通航船舶的问题。