基于集成算法的铁路客流短期预测模型研究

刘 杰

(重庆工程职业技术学院 智能制造与交通学院，402260)

0 引 言

客流预测是铁路运营管理中一项重要的基本工作，科学合理的把握线路乃至路网客流状态，能为铁路的收益管理和决策提供数据支持。预测分为短、中、长期预测，由于中长期预测时间跨度较大，除自身历史客流数据规律外，还要更多考虑经济社会政策突变因素影响。短期预测时间跨度小，在历史数据较为充足的情况下，短期客流可以通过对历史客流数据规律挖掘来较为精确的预测。

目前，客流预测研究成果多集中在短期客流预测。王洪业等[1]以客票系统数据为基础，将客票数据转换为客运量时序数据，采用改进的移动平均法对客流进行预测；李夏苗等[2]基于模糊预测和客流OD推算方法对一条高速铁路线路车站发送人数进行预测，得到较好的效果；杨晓等[3]考虑高速铁路短期客流周期性和波动性特征，提出改进重力模型对客流进行预测；帅斌等[4]根据北京市郊客流的特点，利用灰色预测模型对S2线客流进行了预测，得到了较高的预测精度；李晓俊等[5]基于客流复杂性和非线性特点建立径向基神经网络预测模型；宋嘉雯等[6]基于铁路客流性质提出四阶段法对银川—宁乐铁路初、中、长期客流分别预测；豆飞等[7]把客流变化率模糊化，并利用其模糊值时序关系建立客运专线模糊k近邻预测模型；李丽辉等[8-9]将灰色预测模型和双约束重力模型组合起来对京沪高铁客流进行预测；杨军等[10]提出利用小波分解将原始客流时序数据分为高频和低频2个子序列，再利用SVM回归算法分别对高频和低频子序列进行预测，最后用小波重构得到预测值的地铁客流预测方法；T.H.TSAI等[11]利用多时间单元神经网络和并行集成神经网络对铁路短期客流进行预测，结果表明其在均方误差上明显优于传统多层感知机模型；YU Wei等[12]将经验模态分解和反向传播神经网络模型结合对地铁客流短期预测，得到精度较高且稳定的结果； JIANG Xiushan等[13]将集合经验模态分解和灰色支持向量机结合对武汉—广州高铁客流进行短期预测，结果表明其平均误差小于既有的支持向量机和ARIMA模型预测结果；M.MILENKOVIC等[14]利用季节自回归移动平均模型对塞尔维亚铁路2014年1—6月客流预测，取得了较好效果；SUN Yuxing等[15]将小波分解和支持向量机模型结合对北京地铁短期客流进行预测，该方法预测结果精度较高，且稳定性好。

现有铁路客流预测主要分为2大类：①是传统时序预测模型，如ARIMA和GM(1,1)等，这类模型使用简单，但处理复杂非线性能力不强；②基于机器学习的模型，如随机森林、SVM回归和k邻近模型等，这类模型预测精度高，但需要外部特征数据支持，增加了数据收集和分析的难度。为了克服以上模型缺点，在铁路客流短期问题上，笔者研究思路为首先以铁路车站间OD客流为预测对象，再将小波分解和ARIMA模型组合构建单个预测模型(以下简称：弱模型)，最后采用集成算法Adaboost将多个弱模型集成为一个预测模型(以下简称：强模型)，最后在测试集上进行验证。理论上已经证明，集成算法组合的强模型在预测精度和泛化能力上要高于单个弱模型。

1 抽 样

(1)

(2)

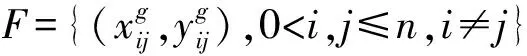
为了后面算法描述方便，将样本集F重新记为F={(xh,yh),h=1,2,…,|F|},其中，|F|表示样本集样本数量。

有了样本集，采用留出法(hold-out)得到训练集U和测试集V，且满足：

|U|∶|V|=4∶1

(3)

|U|+|V|=|F|

(4)

式中：|U|为训练集样本数量；|V|为测试集样本数量。

2 客流预测

ARIMA是一种常用的时间序列建模方法，它不仅描述了数据点之间的相关性，也考虑了数值之间的差异性，但ARIMA模型对数据平稳性有较高要求，铁路客流的时间序列数据很难满足，因此对时间序列先进行小波分解，分解后各子序列相比原始序列更加平稳，更符合ARIMA模型对数据性质的要求，从而可以适当提高预测精度。

2.1 小波分解

考虑客流数据离散特性，采用一维离散小波分解，如式(5)：

(5)

式中：C(0,k)为低频系数；D(l,k)为高频系数；φ(0,k)(h)为尺度函数；ψ(l,k)(h)为小波函数；l和k为整数。

2.2 ARIMA模型

自回归移动平均模型ARIMA[16-17]是基于时间序列数据自相关性，利用历史值和拟合误差的线性组合预测的一种线性模型，如式(6)。ARIMA模型算法流程如图1。

Xt=a1Xt-1+…+apXt-p+εt-…-bqεt-q

(6)

式中：p为自回归阶数；a1,…,ap为自回归系数；q为滑动平均阶数；Xt为t时刻预测值；Xt-1,…,Xt-p为t-1,…,t-p时刻历史数据；εt,εt-1,…,εt-p为t,t-1,…,t-p时刻拟合误差。

图1 ARIMA模型算法预测流程Fig. 1 ARIMA model algorithm prediction process

从小波分解角度，不同的小波基{φ(0,k)(h)，ψ(l,k)(h)，l∈N,k∈Z}得到的低频和高频系数不一样，因此在77种常见小波基中进行筛选，最终选择在样本上加权误差和最小的小波基。算法步骤如下:

步骤2:利用小波基dr对(xh,yh)中特征序列xh分解得到C(0,k)和D(l,k)。

步骤5:如果r=R, 则r=argrmin(Te), 输出dr，算法结束；否则r=r+1，b=0，转步骤2。

3 客流预测集成模型

在特征序列较短时，弱模型的泛化能力不强，为挖掘所有OD客流整体规律，采用Adaboost算法思想将若干个Gm(xh,dr)集成为一个强模型，Gm(xh,dr)表示第m个弱模型，其中m=1,2,…,M,M为弱模型数量。

集成算法是通过样本预测误差更新弱模型权重，最终在损失目标函数达到最优时得到最佳组合[18]。集成算法步骤如下：

步骤1:初始化参数M,μ。其中，μ为防过拟合参数且0<μ<1，令m=1。

步骤2:在U上训练Gm(xh,dr)，得到一个使所有训练样本加权误差最小的Gm(xh,dr)。

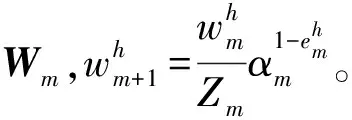
…，αMGM(xh,dr),r∈[1,R]的中位数，算法结束；否则，m=m+1，转步骤2。

4 案例分析

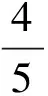
表1 77种常用小波基名称集合Table 1 Name set of 77 kinds of commonly used wavelet bases

4.1 模型参数估计

按第2节中小波基的选择算法确定，最终的小波基为Coiflets 5。按第3节集成算法确定得到100个弱模型权重值如表2。

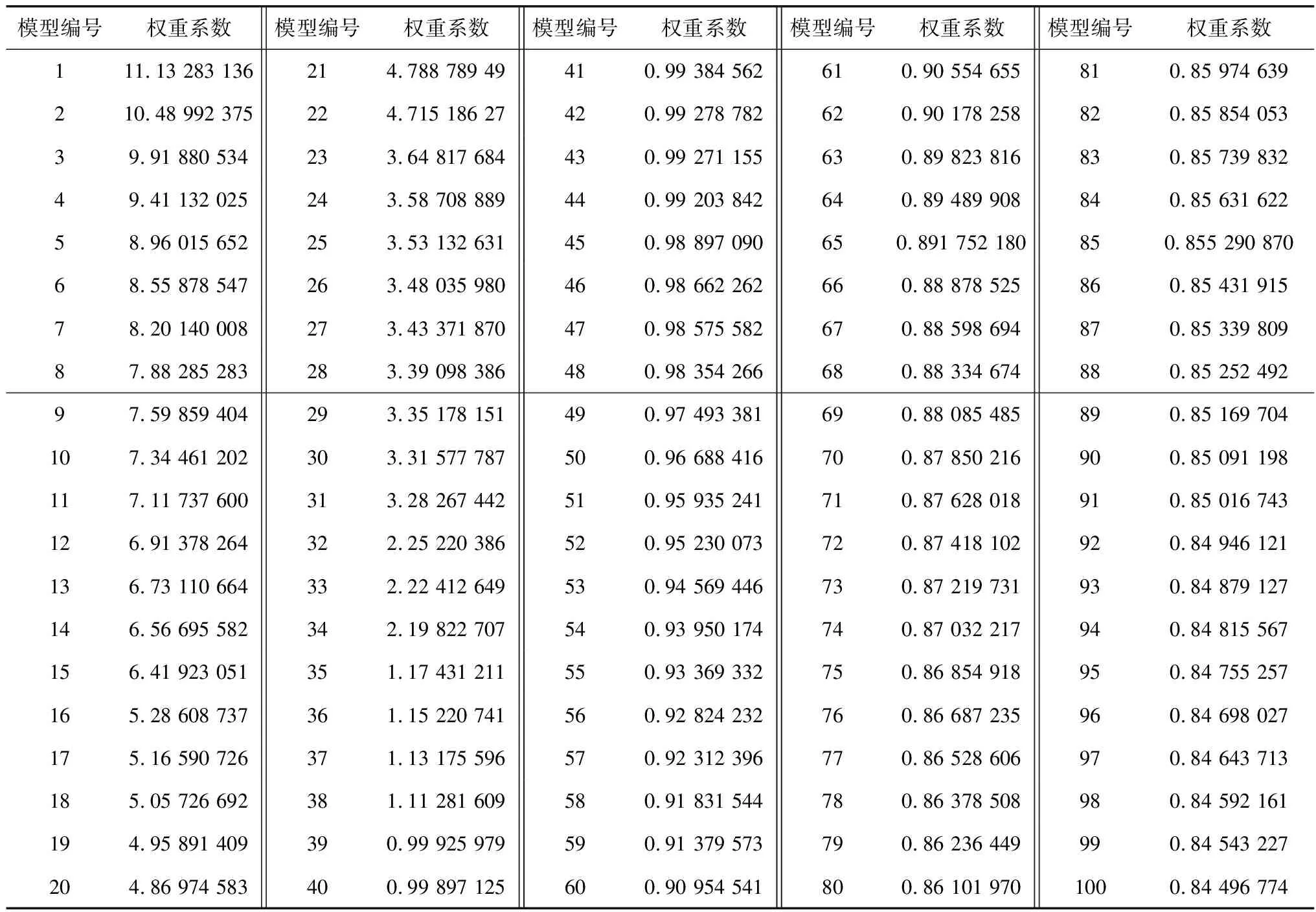
表2 集成模型权重系数Table 2 Weight coefficients of ensemble model

4.2 预测模型精度对比

将测试集V分别用灰色预测模型GM(1,1)，ARIMA同笔者模型分别测试，以平均绝对误差MA、平均相对误差MR和预测均方差MS指标度量，公式如式(7)～式(9)：

(7)

(8)

(9)

表3 模型预测精度结果对比Table 3 Comparison of model prediction accuracy results

表3为模型预测精度结果。由表3可知：笔者模型比GM(1,1)和ARIMA在30天的短期预测上预测精度有明显提高，在MA、MR和MS上与GM(1,1)相比分别提高42.90%、98.61%和63.74%；与ARIMA相比分别提高33.34%、36.94%和13.30%。

从指标结果来看GM(1,1)不适合用来对渝万线特征序列客流进行短期预测，其预测误差过大，原因在于GM(1,1)是以指数形式的变化趋势来进行预测，而特征序列的反复波动性不符合GM(1,1)的特点。ARIMA预测效果优于GM(1,1)，说明渝万线客流除具有周期性和波动性外，还体现一定的线性特征。预测时间跨度越大，预测的累计误差随之增加，精度降低。笔者选择预测时间跨度为30天，在这个时间跨度上获得了较好的精度结果，因此可以将模型和算法泛化到时间跨度小于30天的数据集上。

5 结 语

笔者对数据抽样的变长时间序列样本进行训练与预测，充分挖掘原始时间序列数据局部和全局特征，并和GM(1,1)， ARIMA进行比较。结果表明：在平均绝对误差、平均相对误差和均方差3个指标上平均有38.12%，67.78%和38.52%的提高。笔者模型和算法适用于客流短期预测，但对于中、长期客流预测仅从历史数据特征挖掘是不够的，需要外部数据作为补充，尤其是经济政策的突变影响数据，这也是后续进一步研究的重点。