基于注意力机制LSTM的地铁乘客出行行为预测研究

张鹏飞，翁小雄

(华南理工大学 土木与交通学院，广州 广东 510641)

0 引 言

地铁客流预测是轨道交通领域的研究热点，现有预测模型与方法[1-2]已可以提供相当准确的预测结果，为地铁系统的规划、运营等提供了良好的支撑。然而，随着人工智能、云计算等[3]新技术的飞速发展，地铁领域的应用场景正在向着个性化、多样化方向发展，如交通信息个性化推送[4]、差异化票价策略[5-6]等。这些新兴应用场景不仅需要宏观粒度的客流预测，更需要对微观粒度的乘客个体出行行为进行预测与建模。

个体出行行为预测是指基于个体的历史出行行为记录，预测其下一次的出行属性(如出发地、目的地等)。相较于客流预测，个体出行行为预测的研究起步较晚，主要原因是个体出行行为预测需要对海量数据(如GPS轨迹、地铁刷卡记录等)进行分析，对算法设计及算力都有较高要求。近年来，大数据计算使储存和处理海量个体出行轨迹数据成为可能，针对个体出行行为的预测的研究也开始涌现。目前，个体出行行为预测方法主要基于统计学习算法。S.GAMBS等[7]提出了n元出行马尔科夫(n-Mobility Markov Chain)模型，基于个体出行的前n次访问地点预测下一个可能的访问地点；A.MONREALE等[8]提出了基于决策树的T模式树(T-pattern tree)模型，从历史GPS数据中学习个体的出行行为特征然后进行预测；Z.ZHAO等[9]提出一种n元语言模型，并将出行行为预测分为出行决策以及属性决策两个连续的子问题分别进行求解。然而，这些方法并不能很好适用于地铁乘客的出行行为预测。

地铁乘客的出行行为主要以地铁进出站刷卡(AFC)数据的形式储存。AFC数据包括多维时空信息，如进出站站点、进出站时间等。这些信息有着不同的表示形式，如空间信息(如进站站点)是离散的类别数据(categorical data)，而时间信息(如进站时间)则是连续数据。现存方法通常直接将连续的时间信息离散化，再利用马尔科夫等离散模型进行处理，这显然不够精确。个体出行行为还存在长距离依赖，如某些地铁乘客可能会在每周末去往商场站点进行消遣，这种模式每周才出现一次，传统预测方法无法把握这种间隔较长的出行模式。

针对上述问题，笔者提出了一种基于注意力机制LSTM(长短时循环神经网络)的深度学习预测框架，利用地铁系统的AFC数据记录预测乘客的下一次出行行为。提出了不同的特征提取模块处理与融合不同数据类型的时空信息，能更加精确把握乘客的出行信息，克服了传统统计学习模型难以进行数据融合的缺陷；同时，利用注意力机制学习传统统计学习方法无法把握的长距离依赖出行特征，提升预测精度。

1 研究问题定义

为了表述准确，先对所研究预测问题进行数学定义。

出行元组：出行元组r=(a1,a2,…,ak)定义为地铁乘客一次出行的属性集合，其中ai为第i个出行属性。如一次进站点为A站、时间为08:00、出站点为B站、时间为08:10的出行可表示为(A, 08:00, B, 08:10)。

出行序列：地铁乘客u的出行序列S表示该乘客在AFC数据库中最后n次出行的时序排列S={r1,r2,…,rn}，ri表示乘客u在AFC数据库中记录的第i次出行，rn表示乘客u在AFC数据库中记录的最后一次出行。

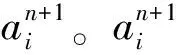
2 基于注意力机制LSTM的预测模型

预测模型的框架主要由特征提取与时序模块两部分组成，如图1。特征提取用于将乘客的各出行属性信息进行融合，从而将出行序列转化为抽象的向量序列输入至时序模块；时序模块基于注意力机制选择与当前预测相关的历史出行信息，生成上下文向量cn，与表示最后一次出行信息的向量hn拼接后输入预测模块，预测下一次出行的出行属性。

2.1 出行特征提取

由于出行属性有离散(空间)和连续(时间)2种数据形式，对不同形式的出行属性信息进行高质量的特征提取及信息融合，对提高预测精度至关重要。针对离散和连续出行属性提出2种不同的特征提取模块，对乘客出行进行建模。

2.1.1 离散出行属性特征提取

离散形式的空间信息数据本质上属于类别数据，如进站站点中每个站点可视作一个分类。对于类别数据，深度学习领域普遍采用词嵌入(word2vec[10])技术进行特征提取，为后续模块提供富含语义特征[11]的高质量输入。笔者利用word2vec将离散出行属性ai变换为对应的非稀疏向量vai。

图1 预测模型框架示意Fig. 1 Schematic diagram of the prediction framework

2.1.2 连续出行属性特征提取

空间信息的连续数据值仅代表不同的时间点，直接将其输入模型无法很好的提取特征，这是由于空间中的连续值并不是预测所需要的信息，预测关注的是地铁乘客在这些时间点上发生出行行为的关联关系，而非数值大小关系。现有预测模型通常对连续时间属性进行离散化，如将一天划分为24个小时区间，将每个区间当作一个类别，然后利用word2vec进行特征提取，这样避免了属性的值对预测造成的影响。

但是，对于地铁乘客的出行行为预测，这种离散化表示并不准确。例如，进站时间08:00与08:59均属于08:00—08:59这个区间，因此若利用小时区间这种离散化形式对时间进行表示，上述两个时间点的表示将完全相同，这掩盖了其实际相差将近一个小时的事实，显然是不合理的。

(1)

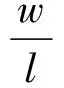
重叠编码的优势在于，当两个时间点接近时，编码绝大多数位置都相同，仅有少数元素不同，可以表征其特征具有很高的相似性。例如图2中，由于07:07与07:14十分相近，他们的重叠编码向量有两处的元素不同(图中只显示了一处)；当两个时间点距离逐渐变大，其相同的元素个数逐渐减少，直至完全没有重叠，此时两个时间点表征不同的两个类别，随后再增加两个时间点间的距离，则不会对其相似性产生影响。

将连续的时间属性表示为重叠编码的形式后，同样利用word2vec将其变换为一个非稀疏向量vai进行特征提取。

2.1.3 出行属性特征融合

利用上述两种特征提取模块，可以将每个出行属性a1,a2,…,ak表示为其对应的非稀疏向量va1,va2,…,vak。深度学习模型具有强大的特征提取能力，可直接将各个非稀疏向量拼接起来组成表征该次出行的特征向量vi=va1⊕va2⊕…⊕vak，其中⊕表示拼接操作。这样，乘客的出行序列S即变换为其对应的向量序列Sv。

2.2 时序预测模块

2.2.1 LSTM神经网络

时序预测模块用于提取序列Sv中的时序关联。长短时记忆神经网络(LSTM)作为一种循环神经网络的改进，对长时序序列有较强的处理能力[12]，其结构如图3。

图3 LSMT结构示意Fig. 3 Schematic diagram of LSTM

LSTM网络的更新规则如式(2)～式(7)：

jt=σ(Wijvt+bij+Whjht-1+bhj)

(2)

ft=σ(Wifvt+bif+Whfht-1+bhf)

(3)

gt=tanh(Wigvt+big+Whght-1+bhg)

(4)

ot=σ(Wiovt+bio+Whoht-1+bho)

(5)

ct=ft*ct-1+jt*gt

(6)

ht=ot*tanh(ct)

(7)

式中：vt为t时刻输入网络的出行特征向量；ht为t时刻LSTM的隐藏层状态向量；jt为记忆状态向量；ht-1为t-1时刻的隐藏层状态向量；it,ft,gt,ot分别为LSTM单元的输入门、遗忘门、记忆门及输出门的输出向量；σ(·)为双曲正切sigmoid激活函数；*为哈达玛(Hadamard)积；Wij,Whj,Wif,Whf,Wig,Whg,Wio,Who均表示一层线性层；bij,bhj,bif,bhf,big,bhg,bio,bho为偏置项。

LSTM主要克服了传统RNN训练中“梯度消失”与“梯度爆炸”的问题。LSTM与传统RNN最大的区别就在于其门控结构对长序列的信息提取更加有效。

2.2.2 注意力模块

虽然LSTM具有提取长序列时序特征的能力，但序列长度过长时(如超过20)，LSTM的性能会快速下降[13]。对于地铁乘客出行行为预测，只有选取足够长的序列长度，才能包含乘客更多的出行特征(如每周末固定休闲出行)。因此，仅利用LSTM无法很好处理地铁乘客出行行为预测问题。

为了解决上述问题，将注意力机制与LSTM组合，共同把握长出行序列的时序特征。注意力机制用于计算乘客的每一次历史出行{r1,r2,…,rn-1}与当前出行rn的相关性，从而构建当前时刻的上下文向量cn。注意力模块的加入使历史特征不会因为多步时序传播而变弱，从而弥补了LSTM无法处理过长序列的缺陷。

上下文向量cn表征当前出行与历史出行的依赖关系，计算方法如式(8)、式(9)：

(8)

αk=softmax(hnWchk)

(9)

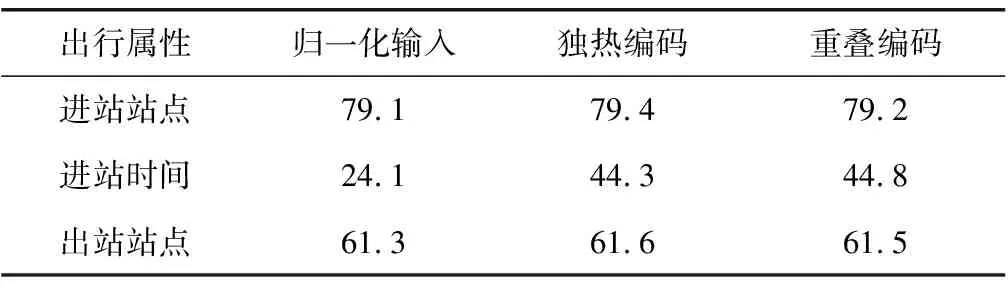
式中：hn，hk分别为当前时刻与k时刻(k

得到上下文向量cn后，将cn与hn拼接后输入线性层，并用softmax激活函数将线性层的输出转化为概率输出：

on=softmax(Woutun)

(10)

式中：Wout为输出线性层，un=cn⊕hn。

2.3 模型训练

L=crossentropy(on,target)

(11)

式中：crossentropy(·)表示交叉熵函数；target为真实属性值对应的独热编码形式。

整体算法训练流程如下：

算法：地铁乘客出行预测训练算法

输入：乘客出行序列S={r1,r2,…,rn}

输出：训练完毕的模型M

while epoch

Sv=featureExtraction (S)

fori∈(1,2,…n) do:

hi=LSTM(vi)

end for

H←[h1,h2,…,hn-1]

cn=Attention(H,hn)

un=cn⊕hn

on=softmax(Woutun)

L=crossentropy(on,target)

IfL

end while

outputM

else:

backpropagation(L)

3 实例分析

以广州地铁2017年1月8日至2017年3月9日的AFC数据验证笔者提出的预测框架。随机选择20 000名累计出行次数大于90次的乘客作为研究对象。对于每次出行，选择进站时间tin，进站站点o，出站站点d以及星期几D构建出行元组。对于每一名所选乘客的出行序列，用宽度为70的滑动时窗进行采样，将所得序列样本按照8∶2比例分为两部分，前80%序列样本归入训练集，后20%序列样本归于测试集。

3.1 特征提取模块性能对比

为验证所提出的特征提取模块的有效性，利用归一化输入、独热编码、重叠编码，3种不同的方法对时间信息进行特征提取：

1)归一化输入。先将时间点tin变换为从当天00:00开始的时间戳，再归一化至区间[0,1]。例如，06:00转换为6÷24=0.25。将归一化后的数值直接与空间信息的非稀疏向量拼接构建vi。

2)独热编码。将时间点tin转换为独热编码(以1 h为间隔)，然后用word2vec转化为非稀疏向量与空间信息拼接。

3)重叠编码。将时间点tin转换为重叠编码(l=5 min,w=1 h)，然后用word2vec转化为非稀疏向量与空间信息拼接。

训练3个分别使用上述3种时间信息表示的模型，分别对下一次出行的进站站点o、进站时间tin及出站站点d进行预测，模型参数设置如表1。

表1 预测模型参数设置Table 1 Parameter settings of the prediction model

vd,vo,vtin,vD分别表示经过word2vec转化后的非稀疏向量。预测的性能指标选择准确率:

(12)

式中：Nright为测试集中对n+1次出行的属性ai预测正确的序列个数；Ntotal为测试集的序列总数。

模型预测结果如表2。

表2 不同时间信息特征提取模块准确率Table 2 Accuracy of different time information feature extraction modules %

实验结果显示：

1)直接归一化输入时间信息无法很好的提取时间特征，其预测性能弱于另外2种方法，尤其是对于进站时间的预测，其准确率远低于另外2种方法。

2)在对进、出站点的预测中，利用独热编码时间信息的模型取得了最好的预测效果；而在对进站时间的预测中，重叠编码具有优势。

这种情况的主要原因是进出站的预测对时间信息的依赖不高，算法只需把握空间信息就可以输出正确的预测站点结果。因此，重叠编码更强的时间信息提取能力优势并不明显，相反，由于重叠编码引入了更高维的时间信息表示，更容易陷入过拟合(over-fitting)的麻烦，降低预测性能；而对于进站时间的预测，算法必须正确把握具体的时间特征才能输出正确的结果。重叠编码提取更高质量时间特征的能力可以显示出较大的优势，从而取得了更高的预测准确率。

3.2 预测性能对比

为了验证笔者提出预测框架的有效性，将其预测结果与现存的代表性个体出行预测模型进行比较(对t的预测采用重叠编码方式，对o与d预测采用独热编码方式)。选择Mobility Markov chain(Markov)算法[12]、Mobility N-gram(N-gram)算法[13]作为比较对象，预测性能对比结果如表3。

由表3可知：

1)在进站站点、进站时间以及出站站点的预测中，对比N-gram算法，笔者提出深度学习模型分别获得了17.9%、4.4%、11.3%的提升。这说明了深度学习框架在特征提取与建模方面相较于所对比方法具有明显优势。

2)较之站点预测，进站时间预测的提升较小，这主要是因为乘客出行的时间存在较高的随机性，即使是同一出行行为(例如下班回家)，其出行时间也可能存在较大幅度的变化，这些随机因素很难通过建模去进行捕捉，因此深度学习模型在进行时间预测时也表现出有限的提升；

3)进、出站站点预测提升较大，这是因为同一出行行为的进出站站点不存在较大的随机性，只要所构建的模型可以更好的捕捉乘客的出行特征，就可以作用于预测效果的提升，获得的提升也更为显著。

相较于目前应用较多的传统统计学习方法，笔者提出的预测框架大幅度提高了预测精度。

4 结 论

笔者提出了一种针对地铁乘客出行行为的预测框架。基于乘客出行行为时间信息及空间信息的特点，构建了不同的特征表示及提取模块，可以更加精确的捕捉个体的出行信息；同时，注意力机制LSTM深度学习网络可以精准的从历史出行信息中选择与当前预测最为相关的出行特征，加强了网络对乘客出行行为多重依赖关系的建模，从而提高对个体出行行为预测的精度。相较于传统统计学习算法，笔者提出的算法具有明显优势。分析发现，所提出模型在对进、出站站点的预测中取得了显著提升，预测准确率分别从50.3%、61.5%提升至61.6%、71.4%。同时，不同的信息提取模块对于不同预测场景的作用也呈现出异质性，对于进站及出站站点的预测中，独热编码预测性能最优，分别达到了79.4%、61.6%，而重叠编码对进站时间的预测则具有优秀的性能，准确率达到44.8%。