一种局部阴影下用户侧光伏阵列解析建模方法
2022-05-26郭雨涵李长青鲁兴海
郁 丹,郭雨涵,李长青,唐 人,鲁兴海
(1.浙江华云电力工程设计咨询有限公司,浙江杭州 310000;2.杭州恒龙新能源科技有限公司,浙江杭州 310016)
碳排放是导致温室效应的主要原因之一,为缓解全球变暖问题,各国纷纷出台了碳中和的规划方案,中国也于2020年9 月承诺,力争在2060 年前实现碳中和,这一雄心勃勃的目标必将带动分布式光伏发电的新一轮增长,用户侧光伏电站高比例接入必将成为未来电力和能源系统的趋势[1]。
光伏发电利用入射光能量激发半导体材料中的载流子,使之产生定向流动形成电能。作用在光伏模块表面的辐射度对光伏输出特性的影响极大,用户侧光伏电站接收的辐射度不仅受云、雾等气象条件影响,而且经常遭受附近建筑物阴影的遮蔽,导致光伏电站出力与标况不同,呈多局部峰值形态。给出不同辐射度下光伏电站的出力曲线,不仅可为用户选择不同光伏型号的收益分析提供参考,也可为最大功率点跟踪提供支撑。
为研究用户侧光伏模块阴影下的输出特性,文献[2]和文献[3]分别基于光伏模块输出特性的超越方程,建立了多个模块串并联的Matlab 模型,对不同遮蔽状态下光伏阵列的输出特性进行了仿真分析。由于光伏模块输出特性的隐函数特点,无法以简单的代数方法求解,并且该超越方程本身又包含多个未知参数,不论是超越方程还是其所包含的未知参数,Matlab 的求解手段均为数值计算方法,不仅耗时较长,且容易受初始值的影响。为此,文献[4]利用代数方法求解了光伏输出特性超越方程中的未知参数,将输出电流-电压特性转变为参数已知的超越方程,但该方法在求解输出特性时仍需要利用迭代等数值计算方法。
为简化光伏模块的建模过程,文献[5]通过引入两个参数,给出了光伏阵列非遮蔽情况下输出特性曲线的简化求解方法,文献[6]和文献[7]基于文献[5]的模型,给出了阴影下的光伏阵列输出特性曲线。但上述文献均未对参数的推导过程进行详细论述。文献[8]采用简化的逆幂律模型和四参数模型对阴影下光伏模块的输出特性进行了分析,但在偏压较大时,两个模型均显示出较大误差。
为提高用户侧局部阴影下光伏阵列输出特性曲线的建模精度,考虑到辐照度对光伏输出特性的重要影响,文献[9]给出了基于动态辐照度的光伏阵列阴影模型,文献[10]建立了光伏模块的子系统模型,但文献[9-10]同样需要预先计算超越方程中未知参数的解;文献[11]通过拍摄照片对阵列表面的辐照度进行计算,以给出阴影下准确的光伏阵列输出特性曲线,但拍摄质量受客观条件因素的制约较多;文献[12]则提出了利用随机森林算法对光伏遮蔽情况进行判断的模型,但是该方法需要预先对模型进行训练。
本文提出了一种仅利用厂商给定数据,不需任何迭代等数值计算,且简单、准确的阴影下光伏阵列输出特性曲线建模方法,并以数值迭代为基准,对所得结果的误差进行对比分析,论证所建模型的准确性和可靠性。
1 光伏模块输出特性和迭代求解
描述光伏模块工作机理的模型包括单二极管和双二极管电路两种,双二极管模型虽然在辐照度较低时的精度稍高,却包含较多的未知参数,导致求解难度较大。单二极管模型能在精度和求解难度中取得较好的折中,因此单二极管模型的应用更加广泛。本文同样采用单二极管模型进行分析,如图1 所示。
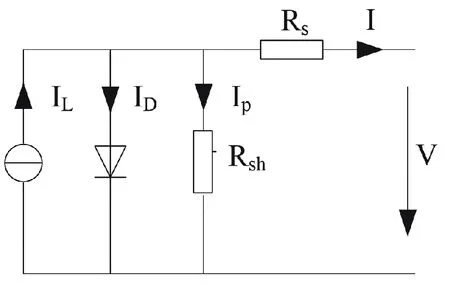
图1 光伏模块的单二极管模型
图1 所示的光伏模块的输出I-V 特性满足:

式中:IL为光生电流;Io为二极管反向暗电流;A为二极管理想因子;Rs为光伏模块的串联电阻;T为光伏模块的工作节温;Rsh为光伏模块的并联电阻;K为玻尔兹曼常数;N为模块中单体电池的串联数;q为电子电量。
式(1)等号左侧的电流变量I同时出现在等号右侧的指数项,不能用简单的代数手段求解,只能利用迭代等数值计算方法给出数值解。由于光伏生产厂家也未给出IL、Io、A、Rs和Rsh的值,因此求解输出特性曲线需要首先计算上述5 个未知参数的值。
将数据手册给定的开路电压(Voc,0)和短路电流点(0,Isc)分别带入式(1),可得:
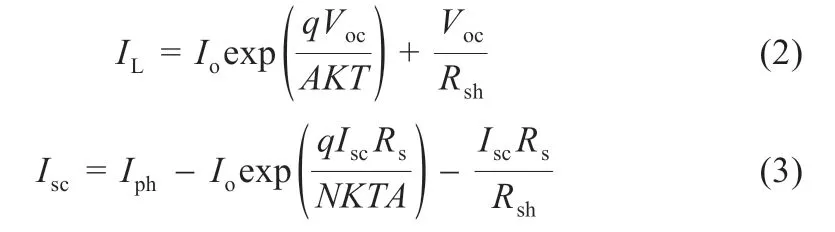
将式(2)带入式(1)得:
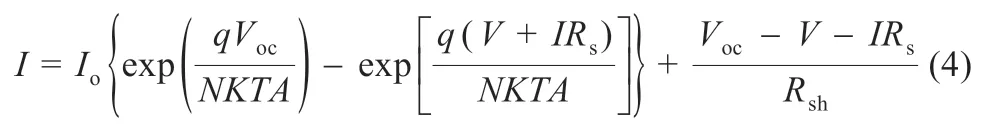
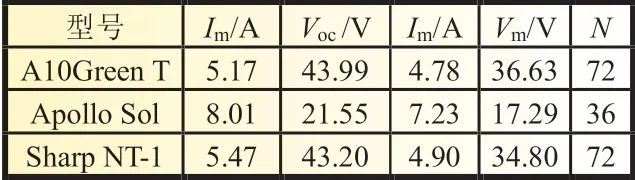
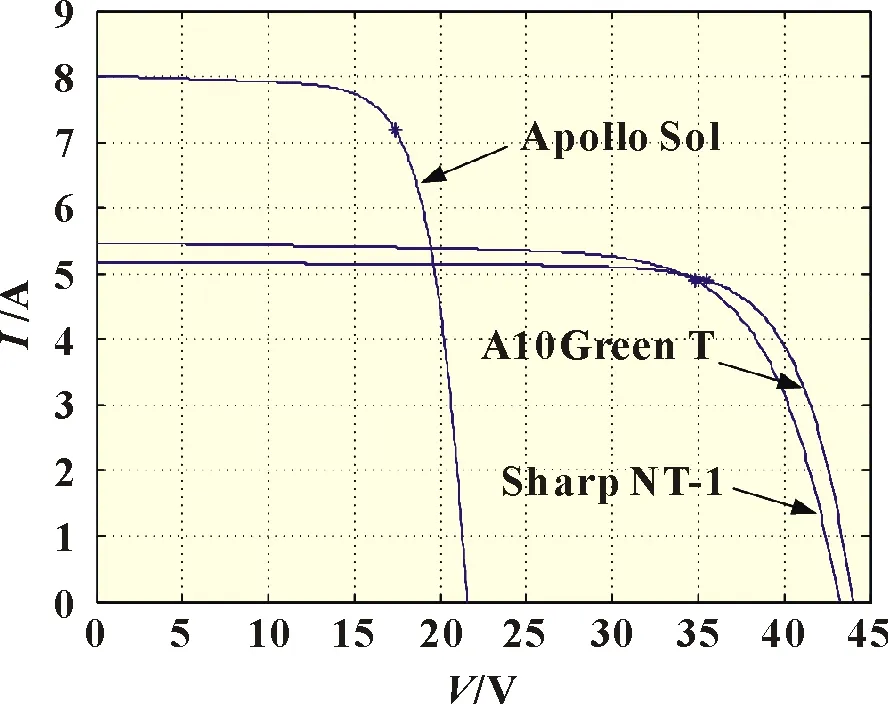
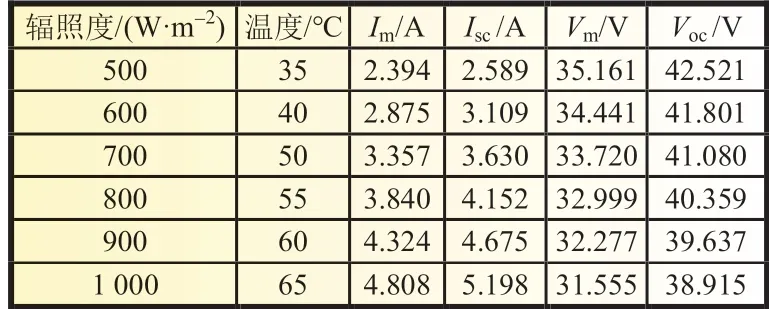
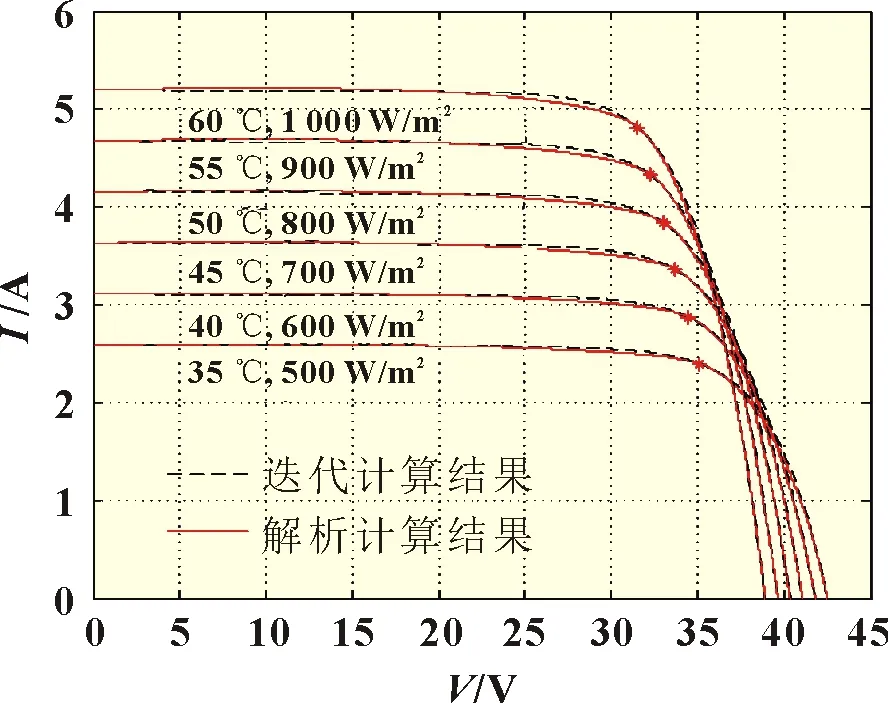
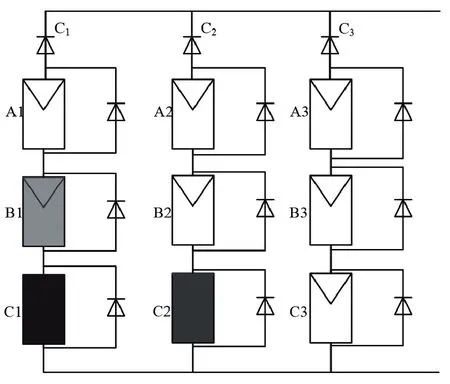
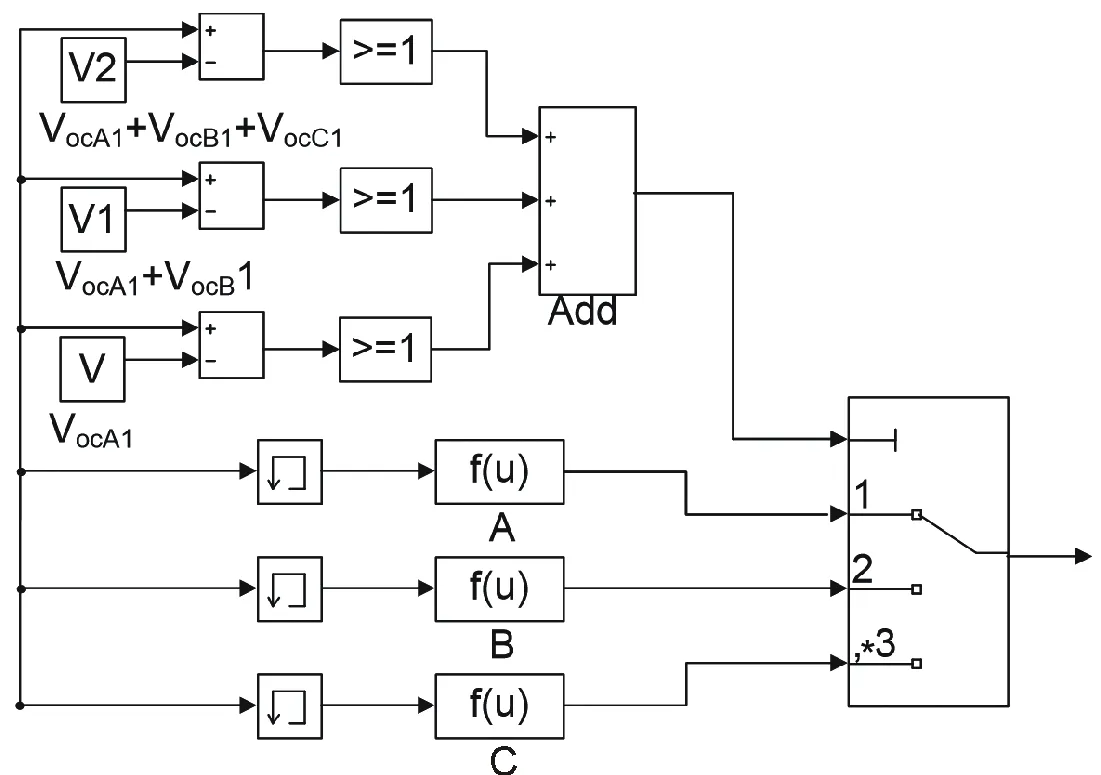
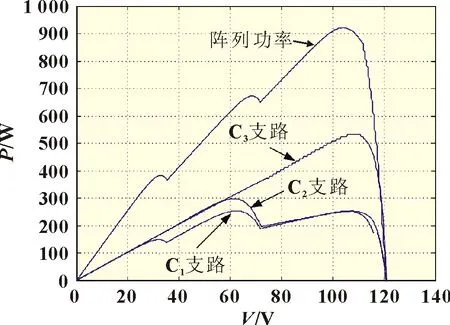
将式(2)带入式(3),且忽略Rs(IscRs< 将最大功率点(Vm,Im)带入(1)可得: 将式(2)、(3)带入式(6)中,消去Io、IL,并进行相应的变换,得到: 由最大功率点处功率对电压导数为0,有: 利用短路电流点(0,Isc)处电流对电压导数等于负的并联电阻的倒数,可得: 综合式(2)、(5)、(7)~(9)可给出光伏非线性方程所有未知参数的解,式(7)~(9)为非线性方程,需进行迭代求解,求解过程中涉及到变量A的值,因而,式(7)~(9)需要迭代计算。式(2)、(5)为代数方程,可在式(7)~(9)计算结果的基础上,直接代数计算。 为验证迭代法计算光伏模块超越方程未知参数的可靠性,选取3 种不同厂家型号的光伏模块,厂家给定数据如表1所示。 表1 光伏组件给定数据 利用表1 中厂商给定参数,对超越方程的5 个未知参数进行计算,结果如表2 所示。 利用表2 中的计算结果,直接调用Matlab 的迭代函数,再次求取3 种光伏模块的输出特性曲线,结果如图2 所示。 表2 光伏组件参数计算结果 图2 光伏模块输出特性迭代计算结果 图2 中利用牛顿迭代数值计算方法给出了3 种不同型号的光伏模块输出特性曲线的数值解,在Matlab2014a 软件上采用迭代法求解上述3 种光伏模块的平均计算时间为7.23 s,求解输出特性的平均时间为3.1 s,迭代求解的计算时间较长。但是和实测值相比,迭代所给出的数值解能够避免客观条件和测量设备所带来的误差。因此,迭代所得的数值解能够作为光伏模块输出特性误差校验的基准。 由于迭代等数值求解光伏模块输出I-V 特性曲线时间较长的弊端,经过大量实践经验的总结,本文给出一种无需迭代计算,仅利用解析方法对标况下(环境温度为25 ℃,辐照度为1 000 W/m2,AM=1.5)光伏组件进行建模的简单方法,光伏模块输出电流满足: 利用式(10)所提模型,基于厂商给定标况下的短路电流点I0(0,Isc)、最大功率点Pm(Vm,Im)和开路电压点V0(Voc,0)数据,即可给出标况下不同光伏模块输出特性曲线的代数求解结果,利用前1 节所给的光伏模块,以式(10)所提模型进行建模,结果如图3 所示。 图3 3种光伏模块输出特性的解析计算结果 图3 中利用所给解析模型对3 种光伏模块进行建模的平均仿真时间为0.7ms,极大地缩短了仿真时间。以迭代数值结果为基准,所提解析模型A10Green T 建模的平均相对误差为2.8%,Apollo Sol 建模的平均相对误差为2.2%,Sharp NT-1建模的平均相对误差为2.3%,平均相对误差小于3%,精度满足工程要求。 光伏模块实际工作时,辐照度和温度经常变化,导致其短路电流点I0(0,Isc)、最大功率点Pm(Vm,Im)和开路电压点V0(Voc,0)的数值发生变化,此时可利用文献[13]给定等式对实际工况下的短路电流点、最大功率点和开路电压点进行计算。 以光伏模块A10Green T 为例,利用文献[13]对实际工况下的短路电流点、最大功率点和开路电压点数值进行计算,结果如表3 所示。 表3 实际工况下的光伏组件数据 基于表3 所得数据,首先以迭代法给出A10Green T 的输出特性,然后利用式(10)的解析模型对A10Green T 的输出特性进行求解,结果如图4 所示。 图4 A10Green T实际工况下的输出特性结果 对变化工况下A10Green T 的输出特性误差进行分析,可知不同辐照度和温度下利用解析法计算A10Green T 的输出特性,其误差和标况下的误差相差不多,不同工况下所有6 条曲线的平均相对误差为2.81%。 基于同样的步骤分别对实际工况下Apollo Sol 和Sharp NT-1 光伏模块的输出特性进行计算,并且其计算结果的平均相对误差同样和标况下误差相近,此处不再给出。 多个光伏模块串并联组成光伏阵列,本文以3 行3 列的光伏阵列为例,利用所建解析模型对该光伏阵列的输出特性进行分析。实际工作时,每个光伏模块均需并联旁路二极管,目的是避免反向击穿的“热斑效应”,同时在每一条光伏模块构成的串联支路均需串联阻塞二极管,目的是防止电流反向流通。 未受阴影遮蔽、轻度阴影遮蔽和阴影遮蔽较严重的光伏模块分别用白色、灰色和黑色表示。假定该光伏阵列的阴影情况如图5 所示。 图5 光伏阵列的阴影情况 对图5 中光伏阵列各串联支路光伏的关键节点的输出特性进行分析。以C1支路为例,假定C1支路中光伏模块C1 受到阴影遮蔽,若该支路总电压为A1、B1 和C1 模块的开路电压之和时,C1支路中所有旁路二极管都处于反偏状态,此时该支路的3 个光伏模块均可向外输出电流,但此时电流为0;若该支路总电压为A1、B1 开路电压之和时,此时输出电流较大,为维持较大的支路电流,光伏模块C1 应处于反偏状态下,A1、B1 可以正常输出电流;同理,若该支路总电压为A1的开路电压时,此时输出电流最大,则此时光伏模块B1 和C1均处于反偏状态下,只有A1 可以正常输出电流。 基于上述分析可知,实际工况下A1、B1 和C1 模块的开路电压分别用VocA1、VocB1和VocC1表示,短路电流分别用IscA1、IscB1和IscC1表示,若该支路总电压在0~VocA1,此时电流输出IscB1~IscA1,若该支路总电压在VocA1~VocA1+VocB1,此时电流输出IscC1~IscB1,若该支路总电压在VocA1+VocB1~VocA1+VocB1+VocC1,此时电流输出0~IscC1。 基于前述理论分析,利用式(10)建立不同辐照度和温度下光伏模块的仿真模型,以其中C1并联支路为例,局部阴影下光伏阵列的仿真模型如图6 所示。 图6 局部阴影下光伏模块的仿真模型 假定图5 中光伏模块结温均为50 ℃,未遮蔽模块的辐照度均为1 000 W/m2,轻度阴影遮蔽的辐照度为800 W/m2,阴影遮蔽较严重模块的辐照度为500 W/m2,利用图6 中所示模型为核心建立Matlab 的仿真分析模型,可以得到任意阴影下光伏阵列输出特性曲线分别如图7、图8 所示。 图7 光伏阵列各串输出I-V曲线 图8 光伏阵列各串输出P-V曲线 由图7 和图8 中A10Green T 阵列的输出特性可知,在温度不变的情况下,辐照度对短路电流和最大功率点电流的影响较大。按照图5 的阴影遮蔽情况,3 行3 列A10Green T 光伏阵列模型的C3支路的输出I-V 特性为一个“台阶”的阶梯波,由于C2和C1支路存在阴影遮蔽的光伏模块的数量分别是1个和2 个,所以C2和C1支路输出I-V 特性为具有2 个和3 个“台阶”的阶梯波,鉴于C1、C2和C3支路最大功率点电压基本相等,所以,整个阵列输出I-V 特性“台阶”的数量与3 条支路中最大“台阶”相同。 利用图7 中的电流和电压数据,保持横轴数据不变,将纵轴设置为电压与电流的乘积即功率,很容易得到图8 所示的光伏阵列P-V 特性,输出的功率特性完全可以用图7 中的I-V特性推导,此处不再详细论述。 针对目前阴影下光伏阵列建模中存在的不足,本文提出了一种不需繁琐数值计算的阴影下光伏阵列输出特性曲线解析建模方法,利用迭代法的数值解为参考,对所提标况和变工况下光伏阵列的输出特性解析方法进行了验证,证明了所提建模方法的简单性和快速性,并给出了3 行3 列光伏阵列在局部阴影下的输出特性曲线的仿真结果,进一步论证了所建模型的准确性和可靠性,可为用户侧光伏阵列阴影下建模提供参考。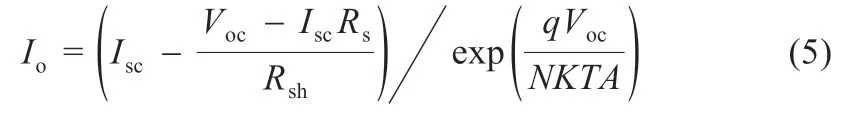
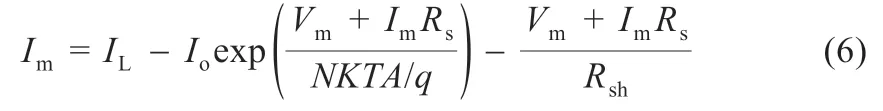
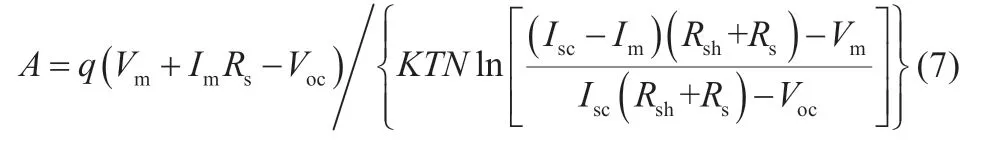
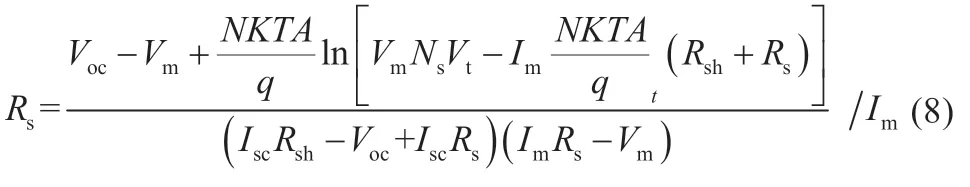
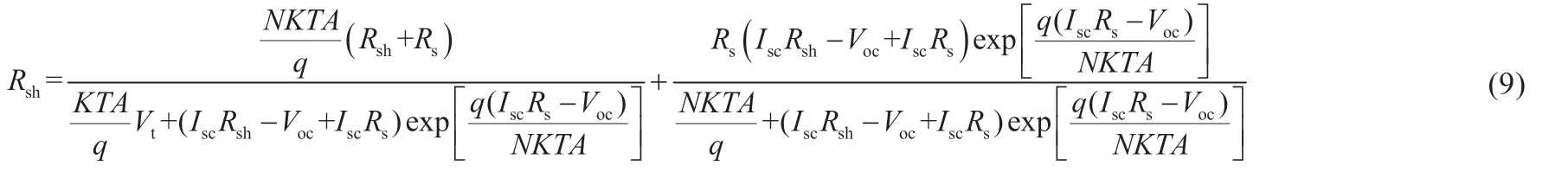

2 光伏模块输出特性的解析模型
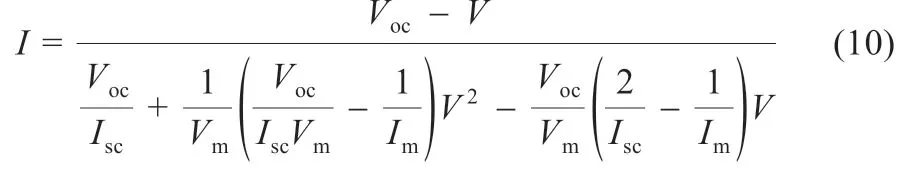

3 局部阴影下光伏模块输出特性

4 结论
