均质软黏土中双筒吸力桩基础最佳荷载作用点不排水承载特性数值分析

2022-05-26王长涛任玉宾张世兴王江宏王凤云

河南科学 2022年4期

王长涛，任玉宾，张世兴，王江宏，王凤云，王胤

（1.海洋石油工程股份有限公司，天津 300451；2.大连理工大学海岸和近海工程国家重点实验室，辽宁大连 116024）

随着海洋资源开发与利用逐渐由近浅海向深远海迈进，深水海洋环境的复杂性与恶劣性对海底工程设施的基础形式提出了更高的要求，将直接导致以下三个问题：①继续采用单吸力桩基础形式则会导致吸力桩尺寸过大，增加陆上加工制造以及海陆运输成本与困难；②深远海海底环境复杂，大直径吸力桩基础的安装成本和施工的困难均会增加；③大直径吸力桩承载力的发挥对荷载作用点和受荷管架可承受的最大应力也提出更高要求.

深水海底平台由于受到海底洋流、管线及上部设施的复杂荷载作用，往往需要采用多个吸力桩进行固定.由多个吸力桩形成的组合桩基础能够保证上部平台结构更加稳固、调节精度更高，能够满足各种新型设备对于平台定位精度的要求，因而组合桩基础形式在深海生产系统中有广阔的应用前景.

对于多筒吸力桩基础，不同的组合形式使得基础在复杂的深海环境中会存在不同的荷载作用位置.已有多位学者研究表明，吸力桩基础的荷载作用点位置对于承载特性有较大影响.目前已知最早的研究为1994年Keaveny等［1］在黏土中进行了多组吸力桩基础水平受荷原位试验，发现不同荷载作用点位置的极限承载力差距可达2倍.Tjelta［2］在2001年研究了不同强度的黏土中最佳荷载作用点的位置，研究发现在均匀强度的黏土中，最佳荷载作用点位置在1/2L，在土体强度随深度线性增加的黏土中，最佳荷载作用点的位置则在2/3L处，且Tjelta指出将荷载作用点施加在筒体某一深度处，吸力桩基础只发生平动，不发生转动，此时吸力桩基础具有最大的承载能力.Supachawarote等［3］通过有限元软件ABAQUS对正常固结土中的吸力桩基础进行承载力分析，研究结果表明当荷载作用点位于0.7L时，其承载力高于其他位置.张其一等［4］利用有限元软件ABAQUS分析吸力桩基础的水平受荷进行分析，研究荷载作用点位置和吸力桩长径比对极限承载力的影响，并给出深水吸力桩失稳模式.研究发现荷载作用点位置极大地影响着吸力桩的极限承载力与稳定性，荷载作用点位置的变化会导致吸力桩出现前倾转动、平移滑动和后仰转动失稳模式，同时吸力桩失稳模式受长径比的影响.王建华等［5］通过室内模型试验对长径比为6和4的吸力桩在0.59L处受荷的极限承载力进行了试验研究，发现当加载角度40°变化至20°时，筒体破坏时的水平位移和承载力逐渐增加，但研究中未能考虑荷载作用点随加载角度的变化关系.黎冰等［6］通过模型试验方式研究砂土中吸力桩基础的承载特性，发现当荷载作用点位于沉箱高度的2/3L和3/4L处时获得的基础承载力最大.

目前，关于双筒基础的承载特性研究较少，尤其是针对双筒基础最佳荷载作用点的承载特性的研究成果更为少见.朱斌等［7-8］通过室内模型试验和离心机试验研究了四锚基础的抗拔和抗倾覆能力，但均考虑的是固定荷载作用点受荷工况，未考虑不同荷载作用点受荷时的承载特性.基于上述研究现状，本文基于有限元软件ABAQUS建立了双筒基础的三维有限元模型，分析了长径比、筒间距、加载角度等因素对双筒基础最佳荷载作用点位置变化的影响，得到了不同工况下双筒基础最佳荷载作用点位置处倾斜受荷的V-H承载力破坏包络线.通过与单筒基础模拟结果的对比，定性计算得到了群桩效应系数，分析了上述三因素对双筒基础承载特性的影响程度.

1 有限元计算模型

与室内模型试验和现场原位测试相比，数值模拟简便快捷，可进行多参数分析，具有一定优势，同时还能获得试验中难以测量的结果.本文基于已有学者的研究方法［9-12］，利用大型商用有限元软件ABAQUS，基于通用静力总应力分析方法对双筒吸力桩基础承载特性开展模拟研究.

1.1 模型建立

双筒吸力桩基础受荷加载位置及角度示意图如图1所示，其中ZP表示荷载作用点距离筒顶平面的竖向距离，HP表示荷载作用点距离吸力筒顶中心处的水平距离；θ表示单个吸力筒受荷方向与水平面的夹角，称为荷载作用角度；S为双筒基础两个吸力筒外侧壁之间的径向距离，称为筒间距.定义与吸力筒受荷方向相同的一侧为前侧，前侧径向正对的一侧为后侧，在双筒基础受荷过程中，筒间为前侧.

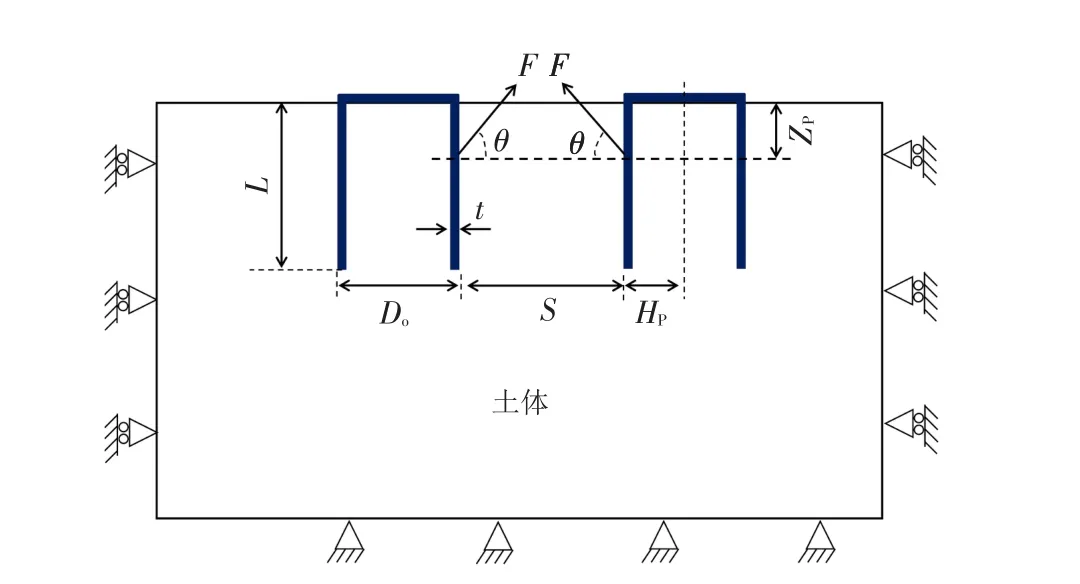
图1 双筒基础受荷示意图Fig.1 Loading schematic diagram of unidirectional loading of double-bucket foundation

由于模型具有对称性，故取双筒基础和土体各一半进行有限元模型的三维建模，建立的双筒基础有限元分析模型如图2所示，其中DB为土体深度方向边界，RB为土体距离吸力筒外侧的径向边界.土体和吸力筒的网格单元采用C3D8R单元进行划分.土体外圆周侧约束两个水平方向的位移，底部约束竖向和水平向三个方向位移，土体上表面自由，土体和双筒基础在对称边界上设置对称边界约束，即位移约束该面法向位移，转动约束只允许沿该面法向转动；采用固定位移比加载方式模拟筒体受荷作用；土体-筒壁间接触采用摩尔-库伦摩擦准则.

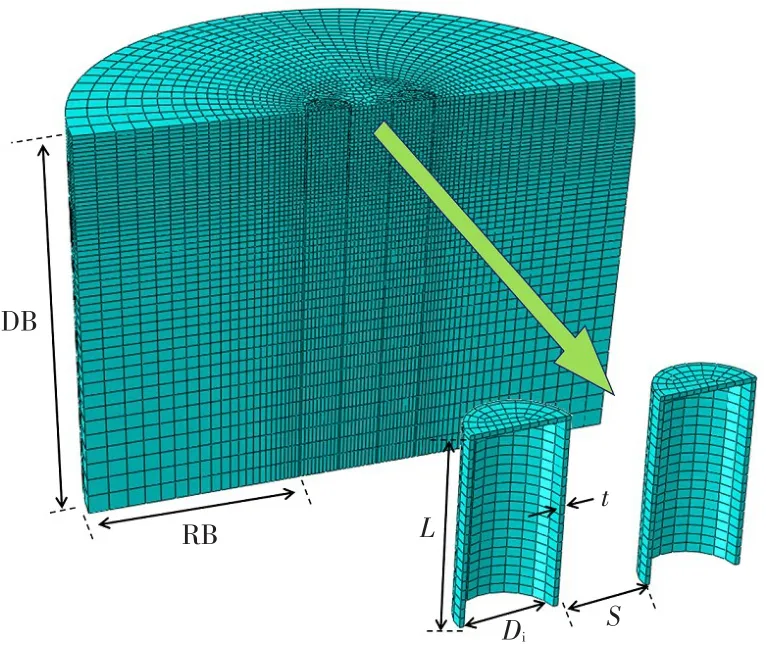
图2 双筒基础受荷有限元模型Fig.2 Finite element model of double-bucket foundation under loads

1.2 材料参数

本研究采用Mohr-Coulomb理想弹塑性本构模型模拟土体应力-应变关系，采用线弹性本构模型模拟吸力筒受力变形.具体参数设置见表1.

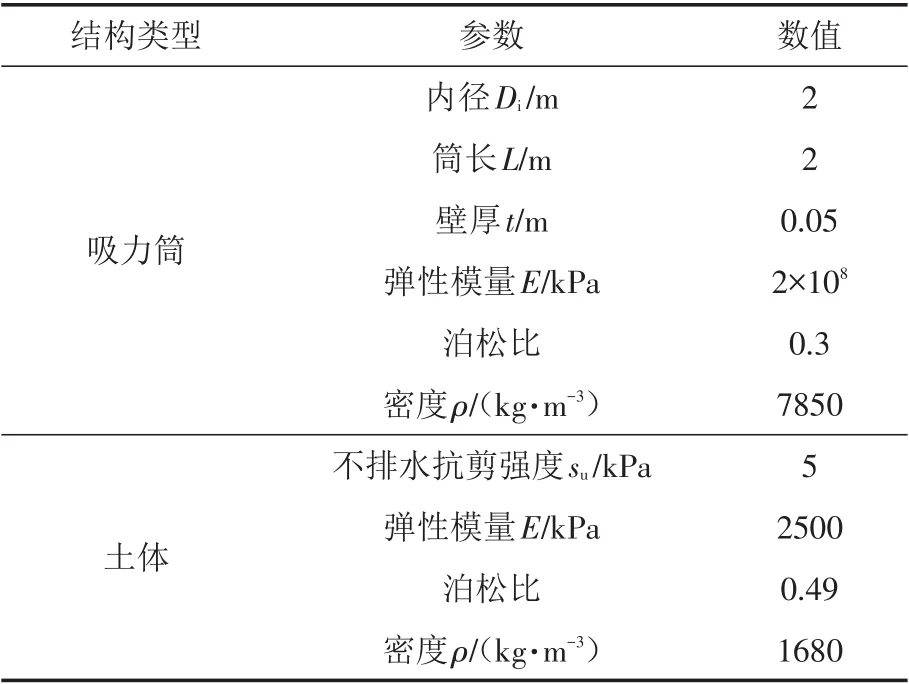
表1 有限元模型中材料参数设置Tab.1 Material parameters of finite element modeling

1.3 荷载位移标记方法

本文采用的荷载位移标记方法，遵循Butterfield等［13］提出的右手准则和顺时针法则，具体标记方法如表2.

表2中F、F1、V1、H1均为不考虑筒重的荷载值；Fult为群桩总极限荷载值；F1ult为单个吸力筒总极限荷载值；V1ult为单个吸力筒竖向极限荷载值；H1ult为单个吸力筒水平向极限荷载值；Di为筒体内径；A为筒顶内部表面积，su为土体不排水抗剪强度；n为筒体个数，本研究模拟双筒，因此取值2.

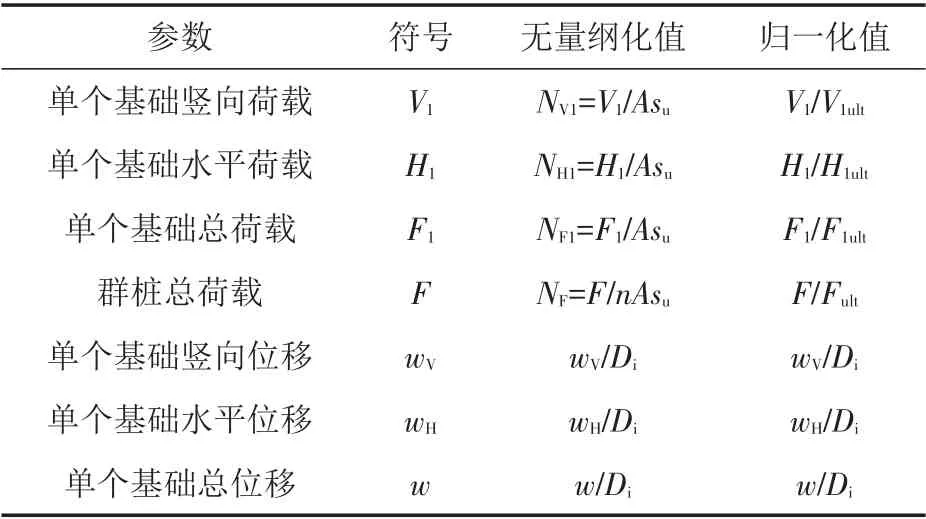
表2 双筒基础荷载位移标记方法Tab.2 Notations for the loads and displacements for double-bucket foundation

讨论群桩效应的影响需结合单筒受荷进行分析，记群桩竖向效应系数为KV=V1/V.其中，V1为群桩工作中单个吸力筒竖向荷载；V为单筒工作时的竖向荷载.相应地，定义群桩水平向效应系数KH=H1/H.

1.4 极限承载力判断标准

本研究采用切线交点法确定吸力筒极限承载力［8，14-16］.该方法是Mansur和Kaufman等［17］于1958年在路易斯安那州河流中进行桩基础承载力测试中提出，并被后来学者所广泛应用的一种基础承载力确定方法.在该方法中，取荷载初始段切线与荷载趋于平缓段切线的交点所对应的荷载值，作为吸力筒基础极限承载力，此极限承载力对应的位移为极限位移，如图3所示.

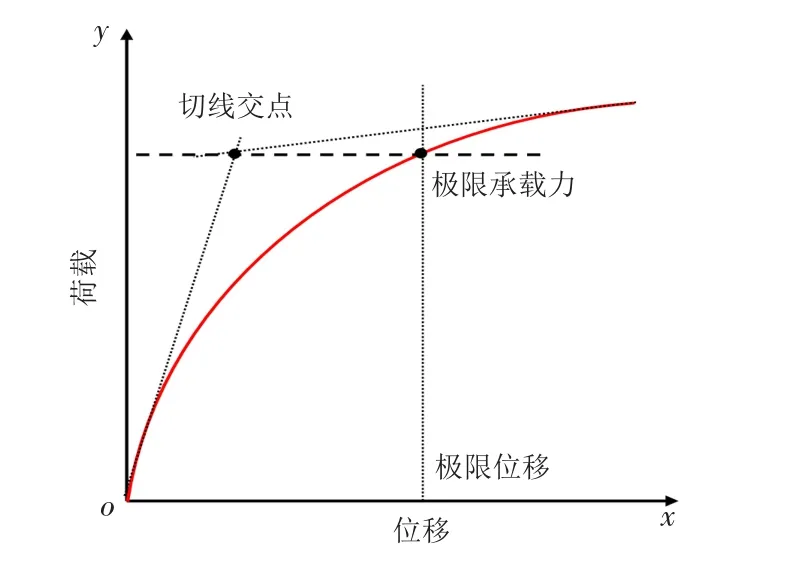
图3 切线交点法确定极限承载力示意图Fig.3 Schematic diagram of ultimate bearing capacity determined by tangent intersection method

1.5 模型有效性验证

为验证本文所建立吸力筒基础有限元模型的有效性与合理性，使用Zhu等［8］和Cao［18］进行的软黏土中单筒受荷离心模型试验结果与数值模拟进行对比.离心模型试验中吸力筒和土体的参数见表3.

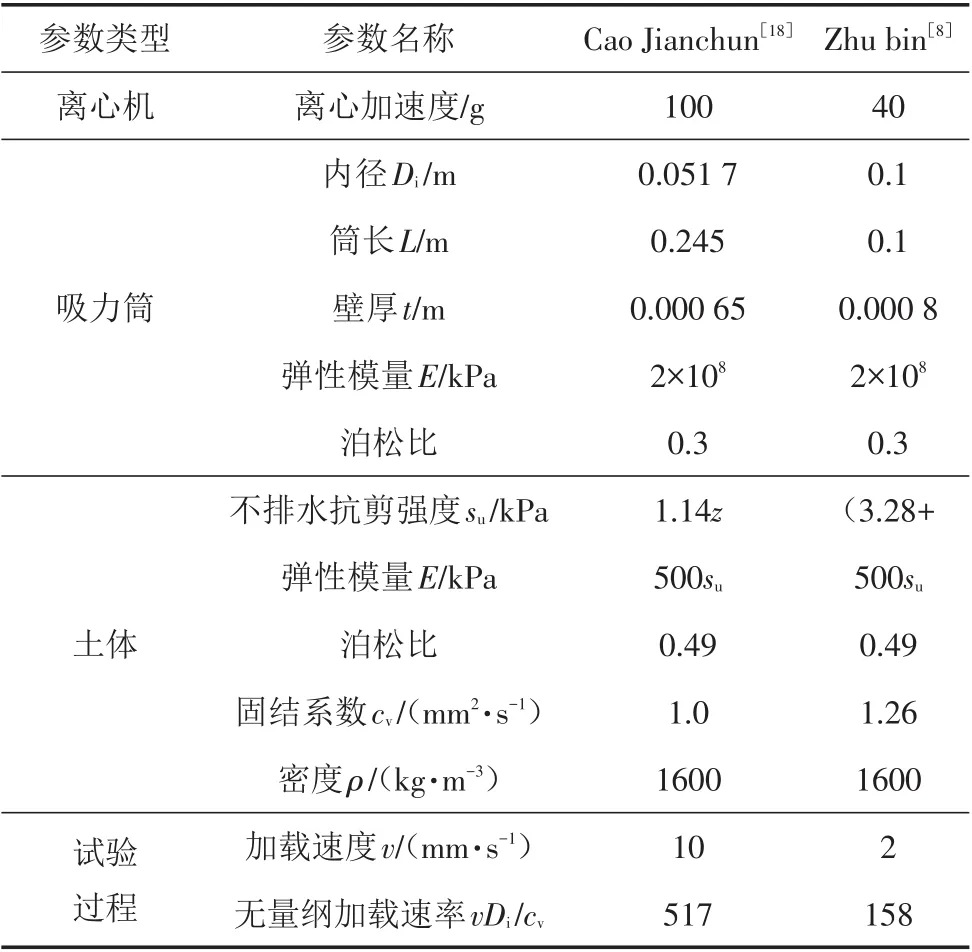
表3 吸力筒离心机受荷模型试验参数Tab.3 The parameters of the suction bucket in centrifuge test

根据Finnie和Randolph［19］在1994年提出的浅基础排水条件判定标准，即无量纲加载速率vDi/cv＞30为不排水条件，0.01＜vDi/cv＜30为部分排水条件，vDi/cv≤0.01为完全排水条件.从表3中所列的2组吸力筒受荷离心模型试验可判断条件为vDi/cv＞30，均为不排水条件试验，与本文建立的吸力筒受荷过程模拟的排水条件一致.同时采用Iskander等［20］提出的吸力筒承载力计算公式对数值模拟结果加以验证，该理论公式表达如下：

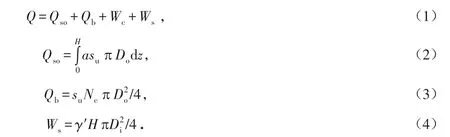
式中：Qso为筒外壁摩擦力；Qb为筒端承载力；Wc为筒体浮重度；Ws为筒内土塞浮重度；a为黏滞系数，Randolph和House［21］认为a一般取值在0.5～0.7之间；su为土体不排水抗剪强度；Di和Do分别为筒体的内直径与外直径；γ′为土体的有效重度；Nc为端部承载力系数，Iskander等［20］、Randolph和House［21］建议取值为9.

数值模拟分别与离心模型试验、理论公式对比如图4所示.

图4 数值模型有效性验证Fig.4 The validation of finite element model

从图4中可以看出，数值模拟得到的荷载-位移曲线中荷载值较离心模型试验测试结果偏大，相对误差具体数值见表4.

表4 数值模拟与试验、理论值对比结果Tab.4 Comparison results of finite element model with experimental and theoretical values

综上，关于数值模拟和离心机试验以及理论公式的对比结果误差均小于10%，可认为本文建立的吸力筒基础受荷有限元计算模型是合理有效的.

2 最佳荷载作用点判别标准

吸力筒基础在海底设施工程中主要承受海底洋流和上部结构共同引起的荷载作用，提高上部荷载作用下的吸力筒基础承载力是工程设计中关注的重点问题，而荷载作用点位置影响着吸力筒基础承载特性和破坏模式，当荷载作用点位于最佳加载位置时，吸力筒基础承载性能得到最大发挥.图5展示了长径比L/Di=2.0，筒间距S/Di=2.0的双筒基础在加载角度为40°时，不同加载位置作用下双筒基础的破坏模式.

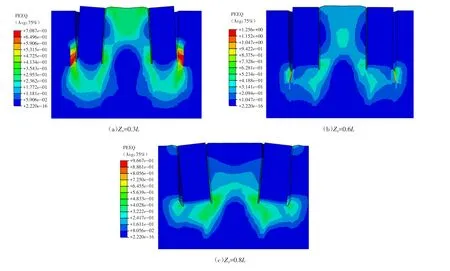
图5 加载位置对双筒基础破坏模式的影响（L/Di=2.0，S/Di=2.0）Fig.5 Influence of loading position on failure mode of double-bucket foundation（L/Di=2.0，S/Di=2.0）

根据前人研究结论，认为吸力筒基础在最佳荷载作用点受荷时只发生平动不发生转动，且此时具有最大的承载能力［2］，如图5（b）所示.故本节提出两种判断吸力筒基础最佳荷载作用点位置的标准，第一种为位移判断标准，第二种为承载力判断标准.

2.1 位移判断标准

在位移判断标准中，认为吸力筒基础失稳破坏时筒体仅发生平动不发生转动，即沿筒长方向各点的位移相等时，判定该点为最佳荷载作用点.

图6展示了长径比L/Di=2.0、筒间距S/Di=2.0的双筒基础在加载角度为40°时，不同加载位置下单个吸力筒筒体前侧的水平位移随深度变化的结果.可以看出，当加载角度θ=40°，荷载作用点位于0.6L处时，筒体沿筒长方向各点的水平位移相等，均为0.12 m.根据位移判断标准，判定该点为最佳荷载作用点.

图6 双筒基础不同荷载作用点受荷时单个吸力筒水平位移随深度的关系Fig.6 The relationship between horizontal displacement and depth of single bucket under different loading points

2.2 承载力判断标准

在承载力判断标准中，认为吸力筒基础在不同加载点作用下获得最大承载能力时的作用点即为最佳荷载作用点.

图7展示了长径比L/Di=2.0，筒间距S/Di=2.0的双筒基础在加载角度为40°时，不同加载位置下单个吸力筒的荷载位移曲线.可以看出，当受荷角度θ=40°，荷载作用点位于0.6L处时，单个吸力筒模拟获得的荷载位移曲线明显高于其他加载位置.根据承载力判断标准，判定该点为最佳荷载作用点.由此可见，对于本文建立的单筒模型，采用位移和承载力判断标准，获得的最佳荷载作用点一致.

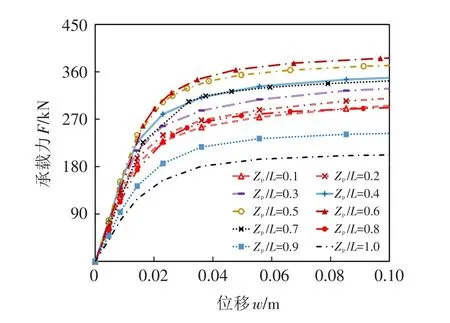
图7 双筒基础不同荷载作用点受荷时单个吸力筒荷载位移曲线Fig.7 Load-displacement curve of single bucket under different loading points

3 计算结果与分析

定义双筒基础中的单个吸力筒发生平移滑动破坏时的荷载作用点为双筒基础的最佳荷载作用点.为了研究双筒基础在最佳荷载作用点处受荷承载特性，进行不同长径比、不同筒间距、不同加载角度工况下的双筒基础受荷分析.本文双筒基础受荷有限元分析模型分析工况参数见表5，其他未列出的材料参数与表1相同.

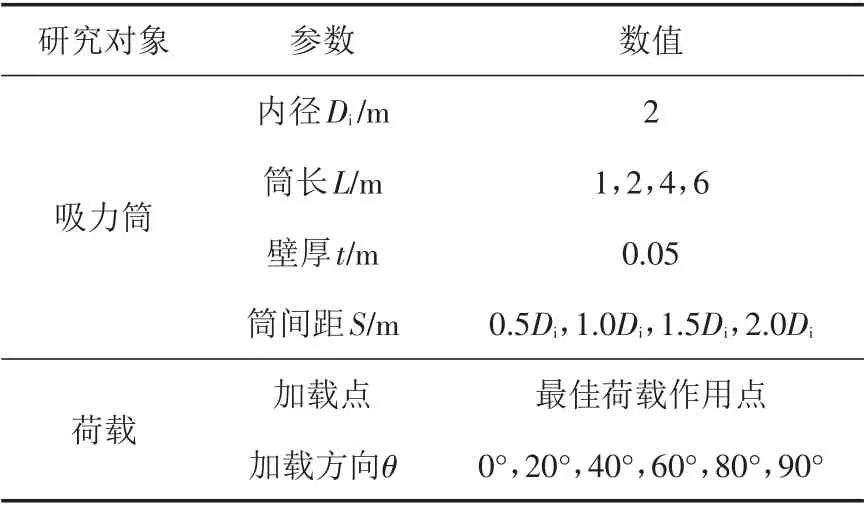
表5 双筒基础受荷分析工况表Tab.5 Load analysis cases for double-bucket foundation

3.1 破坏模式

以长径比L/Di=3.0的双筒基础在筒间距S/Di=2.0工况为例，进行双筒基础周围土体位移和等效塑性应变分析.图8展示了双筒基础在最佳荷载作用点加载角度为0°、40°和80°加载时的筒周土体位移矢量和等效塑性应变分布情况.

从图8中可以看出，①双筒基础及其筒内土体在受荷过程中，仅发生沿加载方向的平移滑动，无转动；②筒体前侧中间土体受挤压向上隆起，筒体后侧土体有向下运动的趋势；③筒体周围土体的等效塑性区关于双筒基础中轴面对称，筒体后侧塑性区发展极不均匀，随着加载角度增大，后侧塑性区逐渐向上扩展；④筒体前侧中间区域土体的塑性变形较为均匀，随着加载角度增大，该区域的塑性变形逐渐减小，筒挤土效应逐渐降低；⑤随着加载角度增大，筒体前侧与后侧以及端部土体的塑性变形逐渐均匀.可推测当筒间距较大且以90°加载角度情况下，双筒基础在受荷过程中，前后侧土体的变形与塑性区的发展相同且均匀.

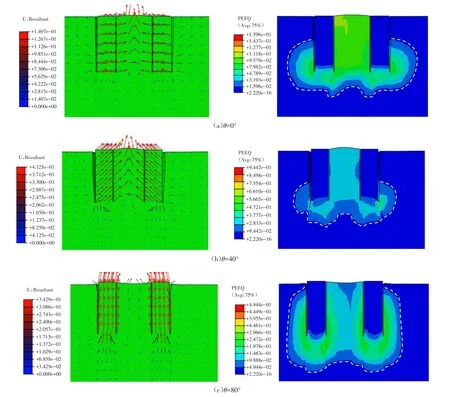
图8 双筒基础最佳荷载作用点受荷土体位移矢量和等效塑性应变分布图（L/Di=3.0，S/Di=2.0）Fig.8 Displacement vector and equivalent plastic strain distribution diagram of the loaded soil on the optimal loading point of the double-bucket foundation（L/Di=3.0，S/Di=2.0）

3.2 极限承载力

进一步研究双筒基础在最佳荷载作用点加载的极限承载力随加载角度变化的发展规律.图9展示了长径比为L/Di=3.0、筒间距S/Di=0.5的双筒基础在最佳荷载作用点处，以不同加载角度加载时获得的单个吸力筒基础荷载-位移关系曲线.从图9（a）可以看出，双筒基础受荷时竖向极限承载力随着加载角度的增大逐渐增大，单个基础的最大竖向荷载发生在90°加载角度下，最小竖向荷载发生在0°加载角度下；从图9（b）可以看出，双筒基础受荷时水平向极限承载力随着加载角度的增大逐渐减小，且在加载角度小于20°之前缓慢减小，最大的水平向承载力发生在0°加载时，最小的水平向承载力发生在90°加载角度下.

图9 双筒基础最佳荷载作用点受荷单个吸力筒荷载位移关系（L/Di=3.0，S/Di=0.5）Fig.9 Load-displacement relationship of the loaded single bucket of optimal loading point for double-bucket foundation（L/Di=3.0，S/Di=0.5）

3.3 V-H破坏包络线

图10展示了筒体长径比为L/Di为0.5、1.0、2.0、3.0，筒间距为S/Di为0.5、1.0、1.5、2.0的工况下，双筒基础在最佳荷载作用点加载时单个吸力筒基础归一化的V-H破坏包络线，可见各工况下V-H破坏包络线变化趋势基本相似.

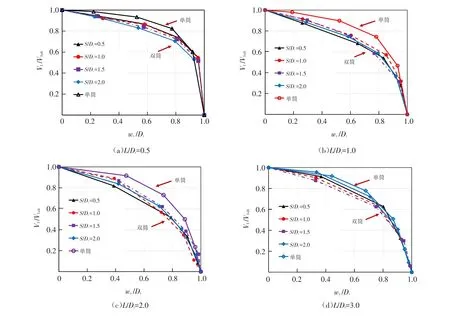
图10 双筒基础最佳荷载作用点受荷单个吸力筒V-H破坏包络线Fig.10 V-H capacity envelope of the loaded single bucket of the optimal loading point for double-bucket foundation

从图10（a）可以看出，长径比L/Di=0.5时，随着筒间距S/Di的增大，双筒基础中的单个吸力筒基础的归一化V-H破坏包络线范围逐渐缩小，且均小于图10单筒最佳荷载作用点受荷时获得的归一化V-H破坏包络线.从图10（b）、（c）、（d）可以看出，长径比L/Di为1.0、2.0、3.0时，不同筒间距工况下获得的归一化的V-H破坏包络线随筒间距的增大变化规律不一致，但均小于单筒最佳荷载作用点受荷时获得的归一化V-H破坏包络线.

3.4 极限破坏位移

已有关于吸力筒基础的研究多是关注承载力问题，然而关于吸力筒基础极限破坏位移的讨论较少，迄今为止尚未有一个广泛认可和应用的破坏标准.

图11和图12分别展示了筒体长径比L/Di为0.5、1.0、2.0、3.0，筒间距S/Di为0.5、1.0、1.5、2.0的工况下，双筒基础在最佳荷载作用点受荷时单个吸力筒基础无量纲化的竖向和水平向极限破坏位移随加载角度的关系.

从图11中可以看出，①在长径比L/Di=0.5时随着加载角度的增加，双筒基础达到极限承载力时竖向极限位移几乎不随加载角度发生变化；在长径比L/Di为1.0、2.0、3.0时，竖向极限位移随着加载角度的增加逐渐增大.②组成双筒基础的单个吸力筒基础在达到极限承载力时，对应的竖向极限破坏位移大于单筒破坏时的竖向极限破坏位移，该结论同Zhu等［8］在离心机中开展的四筒基础竖向抗拔结果不同，而与刘树杰等［22］开展的三筒基础竖向承载力有限元结果相同.③综合4种长径比、4种筒间距的竖向极限破坏位移范围，可认为双筒基础最佳荷载作用点受荷时竖向极限破坏位移在（0.01～0.04）Di之间.

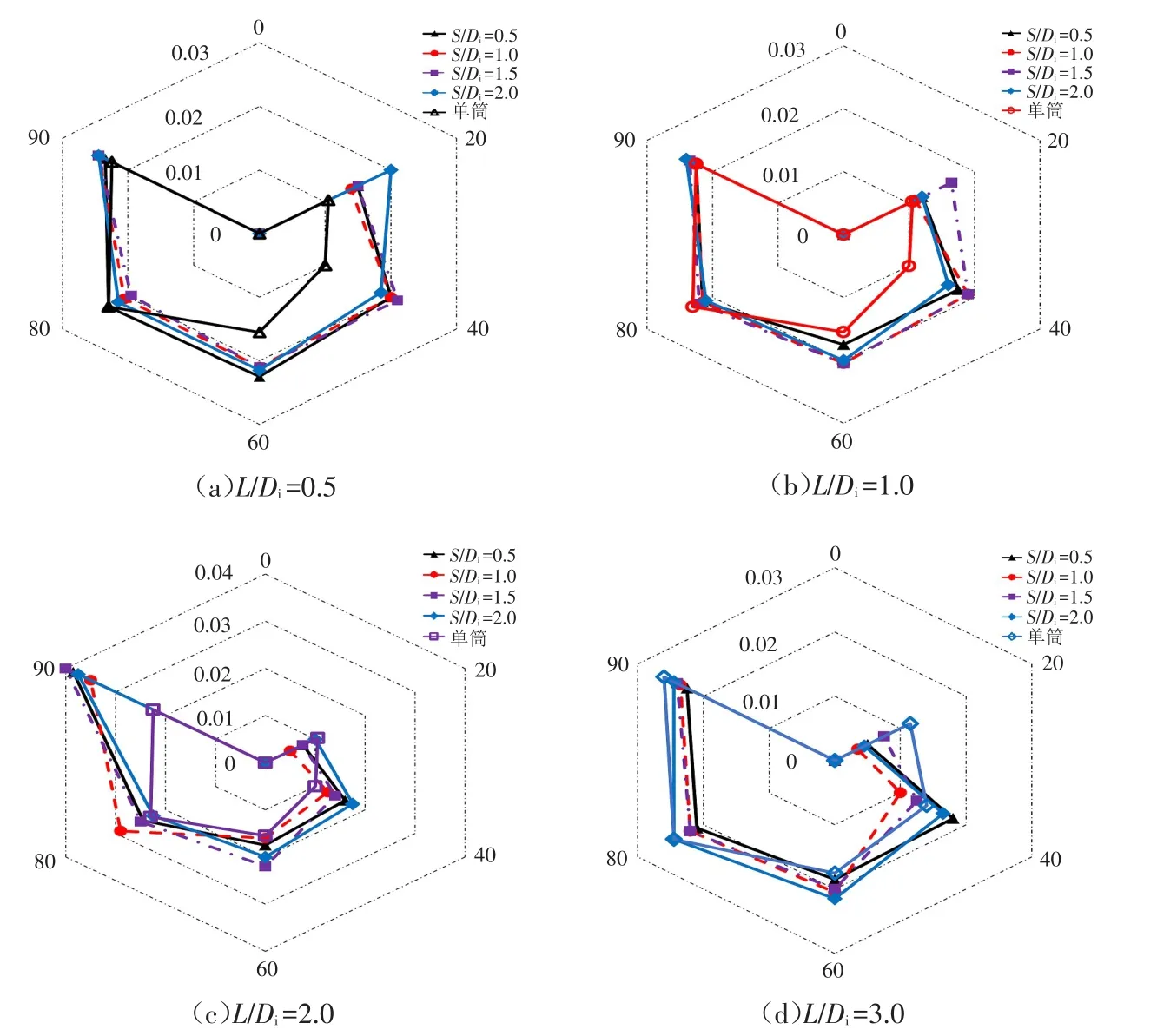
图11 双筒基础在最佳荷载作用点受荷时竖向破坏位移（wv/Di）Fig.11 Vertical failure displacement of suction bucket under load on the optimal loading point（wv/Di）

从图12可以看出，一是随着吸力筒基础加载角度的增加，双筒基础达到极限承载力时水平向极限位移有减小的趋势；二是组成双筒基础的单个吸力筒基础在达到极限承载力时，对应的水平向极限破坏位移与单筒基础水平向极限破坏位移相近；三是综合4种长径比、4种筒间距的竖向极限破坏位移范围，可认为双筒基础最佳荷载作用点受荷时水平向极限破坏位移在（0.01～0.03）Di之间，水平向极限破坏位移要小于竖向极限破坏位移.

图12 双筒基础最佳荷载作用点水平破坏位移（wH/Di）Fig.12 Horizontal failure displacement of suction bucket on the optimal loading point（wH/Di）

3.5 群桩效应

关于长径比L/Di、筒间距S/Di及加载角度θ对双筒基础群桩效应影响的研究目前还不系统.本文基于上文建立的双筒基础最佳荷载作用点受荷有限元模型，基于大量的数值模拟结果，探究双筒基础的竖向和水平向群桩效应系数随着长径比L/Di和筒间距S/Di以及筒顶加载角度θ的变化规律，为双筒基础的优化设计提供借鉴依据.定义双筒竖向群桩效应系数为KV=V1/V，其中V1为组成双筒基础的单个吸力筒竖向极限承载力，V为单筒工作时的竖向极限承载力，相应地，定义水平向群桩效应系数KH=H1/H.

图13展示了同一长径比L/Di的双筒基础最佳荷载作用点以不同角度加载受荷时，KV和KH随着筒间距S/Di和加载角度θ变化的规律.因为加载角度0°时为水平加载，90°时为竖直加载，均为极限工况，故在考虑竖向承载力群筒效应系数KV时，剔除0°受荷工况，考虑水平向承载力群筒系数KH时剔除90°受荷工况.

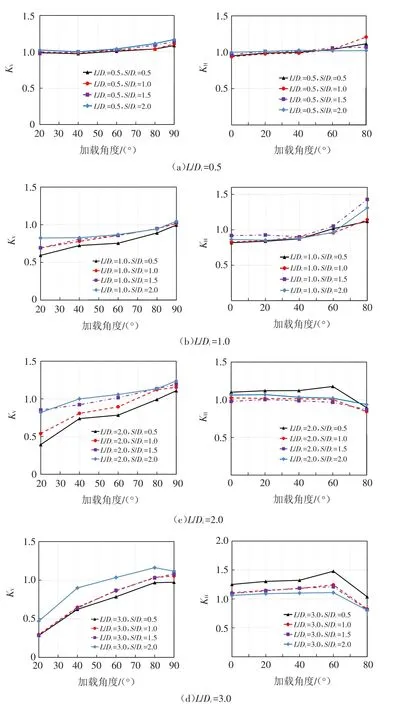
图13 双筒基础最佳荷载作用点受荷时群桩效应系数变化关系Fig.13 The changes of the group pile effect coefficient of the optimal loading point

从图中可以看出，①在加载角度θ≥20°之后，筒间距越大，双筒基础竖向群筒效应系数KV越大.②长径比L/Di=1.0和2.0时，双筒基础竖向群桩效应系数KV随加载角度增加而增大；长径比L/Di=0.5时，双筒基础竖向群桩效应系数KV随加载角度的增加，先稳定在1.0左右而后缓慢增大；长径比L/Di=3.0时，双筒基础竖向群桩效应系数KV随加载角度的增加，先增大而后趋于稳定，即双筒基础最佳荷载作用点的以大角度加载时能得到较大竖向承载力.③双筒基础水平向群桩效应系数KH在不同长径比时随筒间距S/Di和筒顶加载角度θ的变化规律不同.在长径比L/Di=0.5和1.0时，随着加载角度的增加，水平向群桩效应系数KH先发生微小变化后显著增大；在长径比L/Di=2.0时，随着加载角度的增加，水平向群桩效应系数KH先发生微小变化而后显著减小，且筒间距S/Di=0.5获得的水平向群桩效应系数KH最大；在长径比L/Di=3.0时，随着加载角度的增加，水平向群桩效应系数KH先缓慢增加而后减小，且筒间距S/Di=0.5获得的水平向群桩效应系数KH最大.

综上分析，同一长径比的双筒基础群桩效应系数KV和KH随着筒间距S/Di和加载角度θ变化规律并不一致.但筒间距越大，双筒基础竖向群桩效应系数KV越大.当长径比L/Di=0.5时，其KV和KH随加载角度的增大发生微小变化，且稳定在1.0左右，即双筒基础群桩效应不明显；当长径比L/Di=1.0时，加载角度θ≤60°，KV和KH无论筒间距多大，其值均小于1.0，即双筒基础群桩效应是不利的；当长径比L/Di=2.0和3.0时，筒间距S/Di=0.5，获得的水平向群桩效应系数KH最大，但获得的竖向群桩效应系数KV最小.当筒间距S/Di=2.0，获得的竖向群桩效应系数KV最大.

3.6 最佳荷载作用点位置

表6～表9列出了双筒基础不同长径比、不同筒间距受荷时最佳荷载作用点位置随加载角度变化的位置坐标.当Hp/Do=0.5时，意味着最佳荷载作用点位于筒侧，Hp/Do=0时意味着最佳荷载作用点位于筒顶中心位置；当Zp/L=1.0时，意味着最佳荷载作用点位置在筒底端，Zp/L=0时意味着最佳荷载作用点位置在筒顶端.

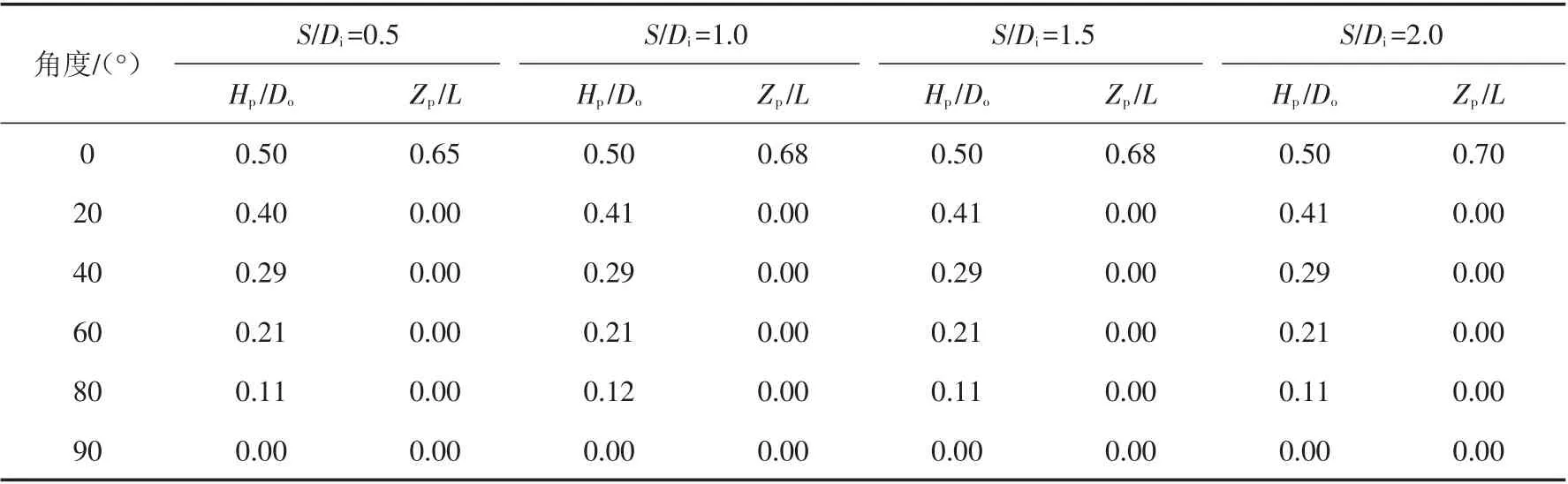
表6 双筒基础最佳荷载作用点位置坐标（L/Di=0.5）Tab.6 Coordinates of the optimal loading point for double-bucket foundation（L/Di=0.5）

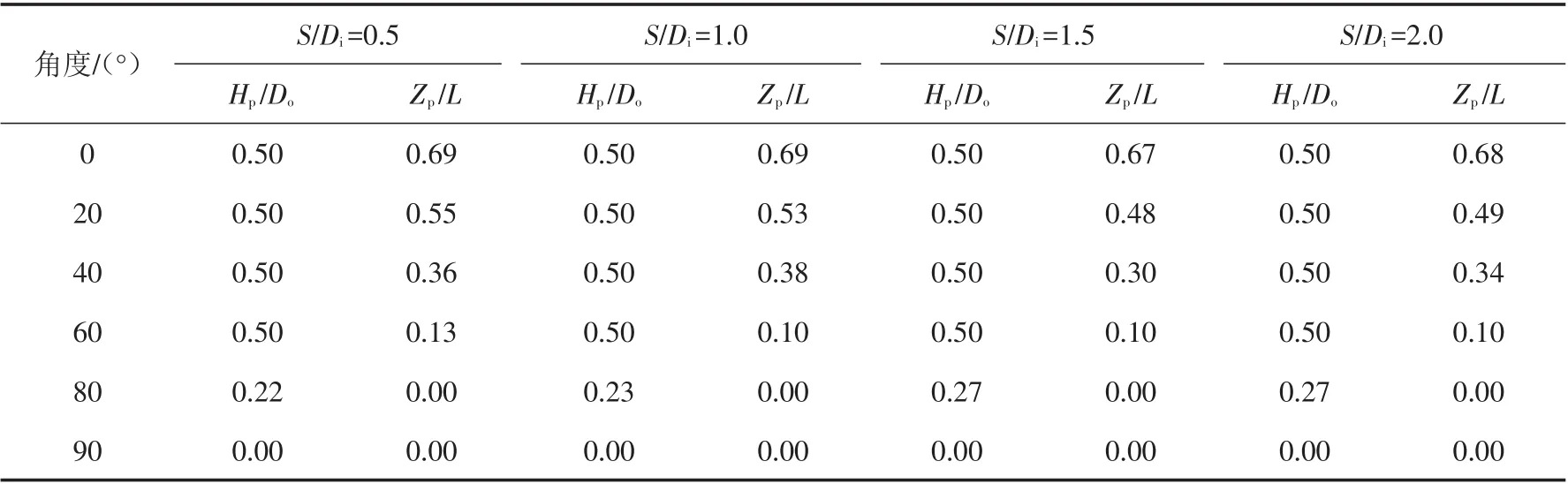
表7 双筒基础最佳荷载作用点位置坐标（L/Di=1.0）Tab.7 Coordinates of the optimal loading point for double-bucket foundation（L/Di=1.0）

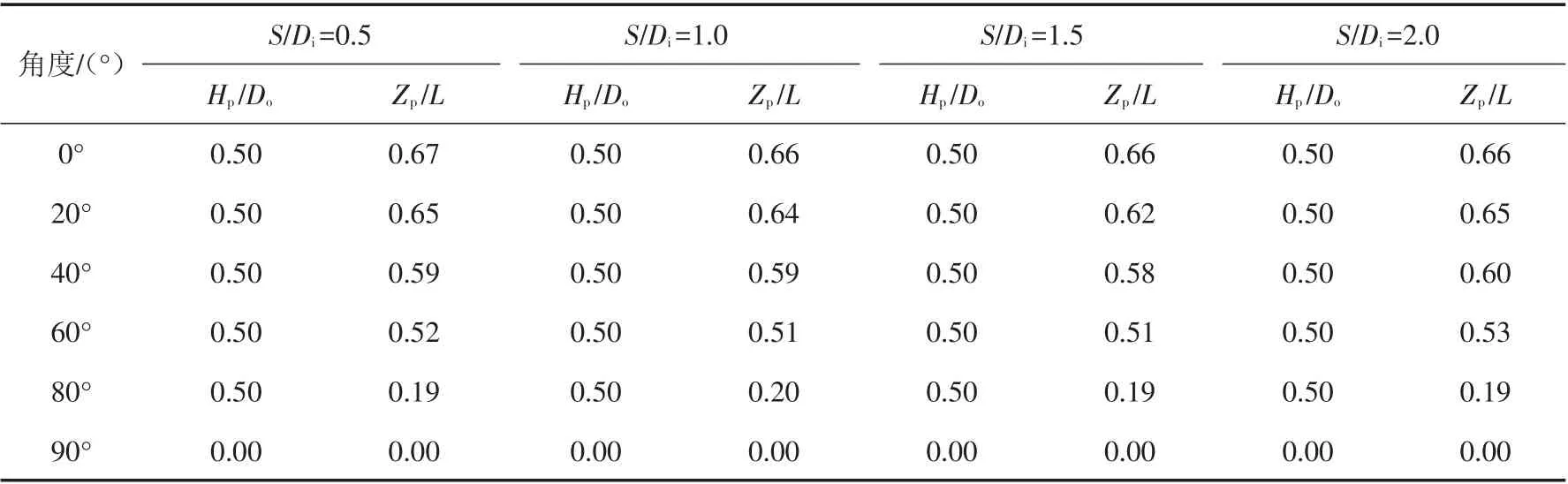
表8 双筒基础最佳荷载作用点位置坐标（L/Di=2.0）Tab.8 Coordinates of the optimal loading point for double-bucket foundation（L/Di=2.0）

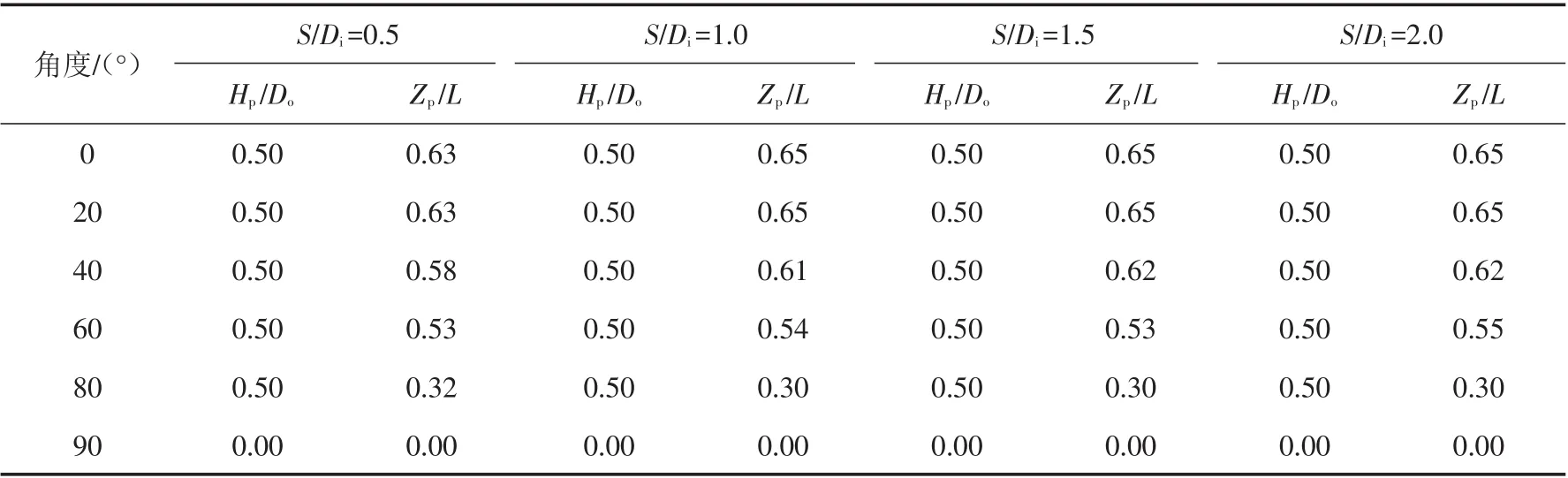
表9 双筒基础最佳荷载作用点位置坐标（L/Di=3.0）Tab.9 Coordinates of the optimal loading point for double-bucket foundation（L/Di=3.0）

为更直接地分析双筒基础受荷时最佳荷载作用点位置随加载角度变化规律，现将最佳荷载作用点位置坐标同加载角度的关系绘于图14中.可以看出，对于长径比为L/Di=0.5的双筒基础，筒间距对其最佳荷载作用点位置的影响非常小，且随着加载角度的增加，Hp/Do值从0.5线性降低至0，即荷载作用点位置离筒顶中心的距离近似线性减小.对于长径比为L/Di=1.0的双筒基础，在加载角度为0°～60°时，Zp/L值随着加载角度的增加从2/3左右逐渐线性降低，即荷载作用点位置离筒顶的距离近似线性减小.对于长径比为L/Di=2.0和3.0的双筒基础，Zp/L数值随着加载角度的增加从2/3左右位置逐渐呈现非线性降低.水平加载时，最佳荷载作用点位置均在筒侧2/3L处；竖向加载时，最佳荷载作用点位置均在筒顶中心处.