纳米结构表面液体沸腾传热的分子动力学模拟

张石重，陈占秀，刘峰瑞，庞润宇，王清

（河北工业大学能源与环境工程学院，天津 300401）

随着电子器件的尺寸不断微型化，功能高度集成及能耗不断增加，对其散热性能要求日趋苛刻，高效散热方式成为制约电子设备性能和可靠性的关键问题。池沸腾强化传热没有运动部件，装置结构简单，池内所需液体量小，适合微型器件狭窄空间内的高热流密度散热，其相变潜热比单相冷却方案高1～3 个数量级，被视作一种重要的有效冷却技术。

微型器件狭窄空间内发生的池沸腾包含复杂的传热与传质过程，加之相变过程的不稳定性，增加了对其实验测试和数值模拟的困难。付婷采用激光加工和烧结技术在金属表面制作微槽和纳米线等不同形状的纳米结构，分析了这些纳米结构对沸腾传热的影响。Ahn 等实验研究了液体饱和状态下光滑及微结构表面对池沸腾的影响。由于目前加工及测试仪器在时间和空间尺度上的限制，采用实验测试方法研究微纳尺度下相变传热依然是具有挑战的课题之一。

采用数值模拟成为微纳尺度行之有效的方法之一。其中分子动力学模拟方法是对分子无原则运动不进行任何简化，是研究原子和分子水平复杂系统的高级确定性方法之一。其优势在于能够以原子级精度描述流体的运动特性，确定每一个原子轨迹，有效得出微纳尺寸下的传热特性，因而成为研究纳米尺度系统沸腾现象的重要工具。

诸多学者利用分子动力学模拟方法对纳米尺度下的沸腾传热过程进行研究，Hens等采用分子动力学模拟研究光滑基底上纳米级厚度液态氩加热沸腾过程，指出对于处在同一温度下的不同浸润性表面，沸腾仅发生在润湿性强的表面。类似地，Mao等利用模拟技术研究了液态水的加热过程，观察到水分子也发生了与Hens 等的工作中类似的沸腾现象。王艳红等从能量角度对沸腾现象进行分析，发现液膜厚度和润湿性共同影响着相变形式：当薄膜厚度较大时，弱的固液间作用力会促进沸腾现象的发生，当厚度较小时，为达到沸腾现象，对壁面提出了更高的温度和润湿性要求；由于较低的Kapitza 热阻，在同一壁面温度下，润湿性强的系统温度梯度更大，在更短时间内有气泡产生。

学者们也对固体壁面上增加微结构强化沸腾传热进行了研究。Chen 等采用分子动力学（molecular dynamics，MD）模拟了凹槽为“V 形”和“柱形”及润湿性对池沸腾液膜上气泡成核行为的影响，发现凹槽结构加速了初始气泡成核时间。Diaz等研究了纳米柱在水平铜基底上氩膜的蒸发及池沸腾传热过程的影响，发现随着纳米柱间距离的增加，热流密度随之增加，最小间距（2.17nm）的热流密度是最大间距（10.66nm）的63%左右。Liu 等利用Weierstrass-Mandelbrot 函数生成了随机粗糙度表面，发现表面粗糙结构提高了换热效率并促进了成核。借助于表面纳米结构，固体和流体原子之间的热传递变得更加有效。Liu 等通过构造凹形半球纳米结构表面，并进行液态氩薄膜在纳米结构表面上的沸腾传热的MD模拟，发现纳米结构可以有效地增强沸腾传热，可以通过增加凹形纳米结构的亲水性来改善传热性能。

本文总结了实验及分子动力学模拟结果，将池沸腾表面微结构概况表述为凹、凸微结构表面，将液膜放置在设有凹、凸半球状纳米结构的粗糙表面进行加热以引发沸腾过程，并与光滑表面进行比较分析；通过在亲水壁面至超疏水壁面7种不同润湿性的表面构建纳米结构，揭示纳米级凹、凸微结构表面和润湿性对液膜池沸腾的综合影响过程。

1 物理模型介绍及模拟细节

本文采用液氩作为传热工质，主要原因是氩以单原子形式存在，氩与氩仅有范德华力作用，没有分子间不对称相互作用、氢键作用及分子间缠绕等，分子振动及碰撞运动单一，反映分子间流动与传热过程简单，很多学者也采用液氩作为流动与传热工质。池沸腾模型中固体壁面以铂（Pt）原子构建，构建的池沸腾结构尺寸参考相关文献[12-19]，计算的体系中凹、凸结构更小，适用于更小的纳米结构对传热的影响，同时将固-液间的作用力范围拓展为超亲水到超疏水状态。

1.1 物理模型

建立如图1 所示的模拟区域，该模拟体系为L×L×L=7.056nm×7.056nm×50.176nm 的 长 方 体 盒子，由固、液和蒸气区域组成。固壁采用Pt原子，依照面心立方结构（FCC）的排列方式构建池沸腾底部金属基板，晶格常数为0.392nm。按照从下至上的顺序，固体基板分别被设置为固定用外部原子、热源和接触墙3个部分，分别起着预防基底形变、提供热源和进行能量交换的作用。固体壁面分为3种结构表面，分别为平面、凸半球纳米结构表面及凹半球纳米结构表面。对于光滑表面，其固体厚度为=3.136nm，液膜厚度为=5.096nm；对于含凸起半球纳米结构的粗糙表面，固体平面的厚度设置为=2.744nm，液膜厚度=5.488nm，纳米结构半径=1.96nm；对于含凹陷半球纳米结构的粗糙表面，固体平面厚度=3.528nm，液膜厚度=4.9nm，纳米结构半径=1.96nm；以上液膜厚度均指液体顶层到平面部分的距离。这些设置保证了氩原子数量在7609 上下，其差距不超过7.5‰。改变壁面厚度及液膜厚度使得氩原子数保持基本不变，由于固体壁面导热层设置较厚且液膜改变较小，这些改动不会对模拟结果造成影响。

图1 物理模型结构示意图

1.2 力场选择及参数设置

将弹簧力施加于固体铂原子，使其被约束在初始位置。工质选用氩原子，其性质稳定，势函数简单，在沿模拟框高度方向的最高处设置反射墙以确保粒子不会丢失。将Lennard-Jones 势能（12-6 势能）模型应用于氩原子、铂原子之间的相互作用力的计算，其中截断半径设置为1.19nm。在本文所有模拟中，基底厚度都超过了其截断半径距离，这保证了壁面厚度不会影响模拟结果。L-J（12-6）势能函数如式(1)所示。

式中，r为计算粒子对之间的间隔距离。在计算氩-氩原子对之间的相互作用力时，两个参数选择为=0.0104eV，=0.3405nm；当计算固体-固体原子对之间的相互作用力时，选取=0.52eV，=0.2475nm。

固体和液体、气体之间的L-J 参数由Lorentz-Berthelot 混合法则进行求解，并使用调节系数对其进行调节，从而获得不同润湿性壁面。其数学形式如式(2)、式(3)所示。

1.3 模拟过程

图2 密度法计算接触角示意图

表1 不同润湿性表面参数

整个模拟过程分为3 个阶段进行。首先利用Nose-Hoover 热浴法进行85K 的热浴，这个阶段选取系综为正则系综（NVT）并使用共轭梯度法对系统能量进行最小化处理，能量公差和力公差均设置为10，保证系统达到稳定状态且粒子速度遵循麦克斯韦速度分布。积分时间步长选择为5fs，进行了3ns 的计算使系统稳定；随后撤去整体温度控制，利用Langevin 控温将基板温度继续控制在85K，同时应用微正则系综（NVE）对全部氩原子进行更新，此过程将会持续1ns，在模拟过程中监测整个系统的温度、压力和能量变化，确保系统在该过程结束之前达到平衡状态，此过程为弛豫过程，保证加热开始前的初始状态；最后一阶段利用Langevin恒温器将热源原子在15ns时间内以43K/ns的升温速率进行升温，其余原子在NVE 环境下进行更新。

2 结果与讨论

2.1 加热相变过程

弛豫后壁面上液态氩层的分布状态如图3 所示。对于光滑平面和凸半球纳米结构表面，所用工况下的形态近似，但是随着接触角增大，固壁与液氩的距离增大。对于凹半球纳米结构表面，润湿性较强的E-case1 至E-case4 工况下，其凹槽内充满工质氩；但是随着接触角增大，即在润湿性较弱的E-case5 至E-case7 工况下，其凹槽内已不再含有工质氩，液氩与固壁间形成部分空腔，如图3(c)所示，说明不同润湿性下固壁与液体层的初始状态不同。

图3 不同壁面工况下的初始状态

对上述初始状态的液氩层进行加热，加热过程液氩沸腾快照如图4所示，对此池沸腾过程中起始沸腾时间进行统计，通过质心位置确定沸腾起始时间，即每隔固定时间取一次液体质心位置，取=+ ∆，此过程上升距离为∆=-，当时间周期为t～t时，h- h< 0.2nm；同时在时间周期为t～t时，h- h> 0.2nm，认为t时刻为沸腾现象发生的沸腾起始时间。统计起始沸腾时间如表2所示。

表2 平面、凹、凸结构表面各工况起始沸腾时间

对于接触角小即润湿性较强的E-case1、Ecase2、E-case3工况，液氩受热后发生爆炸沸腾呈现大致相同的过程，如图4(a)、(b)、(c)所示，在Ecase1的强亲水润湿性下，光滑平面起始沸腾发生在2.7ns左右，凸半球纳米结构表面和凹半球纳米结构表面起始沸腾时间分别是2.25ns和2.175ns；对比亲水条件下逐渐减弱的E-case1、E-case2、E-case3工况，平面上液氩沸腾起始时间由2.7ns 左右逐渐延长为5.4ns 左右，凸半球纳米结构表面起始沸腾时间由2.25ns左右逐渐延长为4.6ns左右，凹半球纳米结构表面起始沸腾时间由2.175ns 左右逐渐延长为4.35ns左右，说明在亲水条件下，相同结构的表面，润湿性减弱延后了气泡出现的起始时间；对于同一润湿性下平面和含凸、凹半球纳米结构的三种亲水性表面，在E-case1亲水工况下，凹半球纳米结构表面发生沸腾所需时间最快，凸半球纳米结构表面次之，平面所需时间最长，说明添加纳米结构会促进气泡提前发生，缩短起始沸腾时间。

疏水工况下E-case4、E-case5 如图4(d)和(e)所示，含凸半球纳米结构表面出现气泡早于含凹半球纳米结构表面，平面还是最晚，与亲水E-case1、E-case2、E-case3 工况不同；E-case4 工况下三种表面均早于E-case5 工况下三种表面；超疏水Ecase6及E-case7，平面和含凹半球纳米结构表面都在10.75ns 有气泡产生，可以计算到起始沸腾时间点，而含凸半球结构表面气泡产生时间点不明显；对于更为疏水工况E-case7，加热至计算完成，只有平面上有气泡产生，约在12.8ns，含凹、凸半球纳米结构表面均没有明显的气泡产生，液膜离开固壁的距离也很小，主要表现为液膜上部氩原子蒸发过程。

图4 不同工况壁面快照信息

2.2 相变过程中气相分子数的变化

本文采用Maroo 等判定气态原子的方法判断加热过程中气相分子数量，以某原子为中心确定其周围5.3nm半径球体内氩原子数目，当该原子周围有不超过7 个氩原子时，认为该原子处于气体状态。通过这种方法计算了上述工况下的气态原子占比，如图5所示，其数值上等于气态原子数目与总的氩原子数目之比。

图5 不同表面加热过程气态原子所占比例

图5所示为加热过程中气态原子生成分数，曲线斜率表示气态原子生成速率。由图5发现气态原子变化可以分为两个阶段，曲线拐点位置在起始沸腾时间点附近。第一阶段是开始加热过程，气态氩原子上升速度很快，气态氩逐渐摆脱液氩层进入气体空间，说明在此阶段液氩层原子在固壁附近吸热，固壁的热量通过液氩层传递到其上层氩原子，上层氩原子吸热后以蒸发方式进入气体空间；第二阶段是沸腾加热过程，气体分子数也在增加，但是增速减缓，直至全部液体原子加热后转变为气态原子，之后气态原子不再增加，曲线不再上升，Ecase1至E-case4工况下在计算时间内液氩全部转变为气态氩；曲线随着润湿性减弱，拐点位置逐渐下移，说明润湿性减弱，液态原子转换为气态原子的速度也随之降低，E-case5 至E-case7 工况下在计算时间内液氩未全部转变为气态氩，且对于超疏水E-case6 和E-case7，液氩转变为气态氩的数量未超过30%。对比三种表面上气态氩生成速度，Ecase1至E-case4工况下，含凹半球微结构表面略大于凸半球微结构表面，两者都大于平面；而对于E-case5 工况，三种表面上气态生成速度相差不大，对于E-case6 和E-case7，平面速度最快，含凹半球微结构表面次之，凸半球微结构表面最慢。

2.3 不同工况下氩膜层温度变化

温度变化曲线如图6～图8所示，温度曲线的斜率反映了液氩层升温速率。图6 是亲水工况Ecase1 至E-case3 下液氩层温度随时间的变化趋势，温度曲线变化过程中也有拐点，此拐点位置也在起始沸腾时间点附近。相同亲水工况下均显示出含凹半球纳米结构表面上液氩温度最高，升温速率最快，含凸半球纳米结构表面次之，平面工况中液氩温度最小和升温速率最慢的顺序，说明相同亲水情况下纳米结构的存在能够强化换热，但润湿性占据主要影响因素，这与前人的研究结果一致。

图6 亲水壁面温度随时间变化情况

温度曲线也可分为两段，曲线转折发生也在起始沸腾时间点附近（约2.7ns），强亲水工况Ecase1 与E-case2 和E-case3 比较，温度升高转折变化比较明显，反映了起始沸腾前液氩在固壁附近的快速升温过程；发生起始沸腾后，液氩层离开壁面，是升温速率减慢的过程。E-case1 至E-case3工况，随着润湿性减弱，升温速度减缓，凸半球微结构表面升温速率最快，凹半球微结构表面次之，平面最弱。

图7 显示了疏水E-case4 和E-case5 工况下液氩层温度随时间变化趋势，两种工况下温度曲线均有转折点，也在起始沸腾时间点附近。E-case4 工况下三种表面上两个阶段的变化趋势比较相近，凹、凸半球纳米结构表面有温度交叉，在4.5ns之前显示出＞＞的温度排序；而在4.5ns之后，如插图P2-Concave-E-case4所示情况，由于纳米凹槽初始状态有液氩原子，三种表面温度变化相差不大。而对于接触角为132.72°的E-Case5工况，开始阶段凸半球纳米结构表面温度升高领先，而由于凹、凸槽内液氩原子蒸发逃逸，使得平面上液氩层的温度升高变快，超过凹、凸槽上液氩温度。

图7 疏水壁面温度随时间变化情况

图8显示了接触角在150°～180°的超疏水E-case6和E-case7 工况下液氩层温度随时间的变化趋势，三种表面上温度曲线转折也在起始沸腾时间点附近，与前面快照图4相符。这种超疏水情况，整体温升情况都比较差，加上初始时刻凹、凸半球纳米结构表面便存在空隙（气泡），直至计算完成，最高温升在115K 范围内。超疏水表面出现的气泡（气体层）初始时刻便存在，不是加热过程形成的，在强疏水表面上固-液间作用力非常小，液氩难以完全浸润壁面，该气体层的出现是固-液弱相互作用力导致，壁面上能量传递效率很低，加热产生气泡出现较晚。这与“壁面越亲水传热效果越好气泡出现越早”是不同的。比较亲水、输水表面上的温升最大相差45K，并且平面上温升大于含微结构表面上的温升，呈现出>>。加热过程结束，液体温度只是从85K提高到100～110K，再一次说明了超疏水表面不适用于强化传热过程。

图8 超疏水壁面温度随时间变化情况

2.4 不同工况下氩原子热流密度变化

热流密度参考了Liu 等的做法，使用氩原子总能量的变化与液态氩薄膜的横截面积的商来获得热流密度，即= ∂(∂·)。式中，和分别表示整个系统氩原子能量增量和系统加热方向的截面面积，选取的截面积均为底面面积。将热流密度随时间的变化曲线记录在图9～图11 中。对于光滑的强润湿性表面，利用本文模拟程序，按照前人的成果中的相应参数进行模拟验证，得到的热流密度趋势与上述文献一致，且热流密度峰值约为0.00305eV/(ps·nm)和0.00312eV/(ps·nm)，与 两 种热流密度峰值0.003eV/( ps·nm)和0.00306 eV/( ps·nm)相差分别为1.67%和1.96%，验证了本文模拟程序的准确性。

图9 所示为亲水E-case1、E-case2、E-case3的热流密度变化曲线，热流密度变化分为三部分，曲线有两次转折变化，统计发现第一个拐点均发生在起始沸腾时间点之前，第二个拐点在时间方面没有总结出明显特征，但是都在液膜离开固壁2nm以上出现，这个问题本文不做深入讨论。

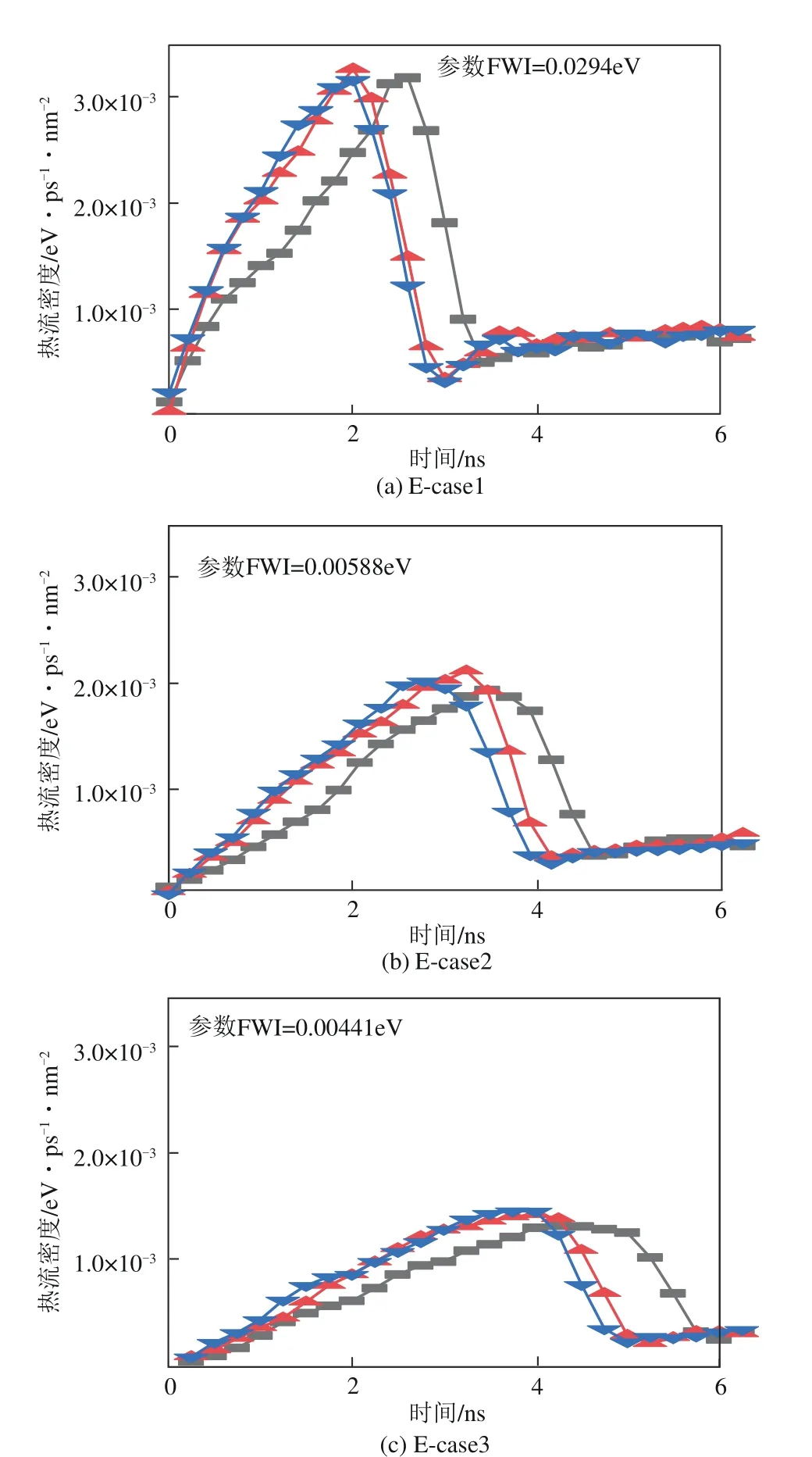
图9 亲水工况热流随时间变化

亲水E-case1至E-case3工况下，含凹半球纳米结构表面上热流密度峰值出现最早，但与凸半球纳米结构表面工况中峰值出现时间相差不大，平面工况中热流密度峰值出现最晚，这说明存在纳米结构能够强化换热，强化效果与纳米结构有关；亲水E-case1、E-case2、E-case3工况下随润湿性减弱，最大热流密度降低，并且需要花费更多时间到达最高热流密度点，相应的下降热流密度也表现出相似性质。

疏水工况的热流变化如图10 所示，疏水Ecase4 工况下热流密度上升与下降的拐点也发生在起始沸腾时间点之前，发生在4ns 附近，直至固-液完全分离后，起始沸腾时间点后，热流密度才陡然下降。说明在疏水E-case4 下，即使产生气泡，发生固-液完全分离，液氩层距离固壁位置也不远，不像亲水表面那样产生较大能量推动液膜远离壁面。而工况E-case5初始时刻，液膜与凹陷处就已分离，6.0～7.0ns期间由于底部加热才发生固-液分离现象，这归因于固-液间弱作用力不能完全被液氩浸润，疏水表面在加热初始时，凹陷纳米结构存在的气泡核将会阻碍热量传递，导致疏水凹半球纳米结构平面的固-液分离时间大幅度延迟。

对于超疏水E-case6和E-case7工况(图11)，热流密度小于疏水工况E-case5，也出现上升和下降过程，含凸半球微结构表面表现有异常，在5.875ns 时便出现了气泡波动，但直至11.435ns 时才发生固-液分离现象，根据气泡质心计算，没有计算得到气泡起始沸腾点。对于超疏水E-case6和E-case7 工况，由于强疏水性导致壁面对氩原子束缚力很小，升高的温度对其稍加扰动，便会产生气泡，出现的气体核反而阻碍了热量传递，导致液膜上层温度较低，无法产生足够的启动压力，导致固-液分离现象出现较晚。

图11 超疏水工况热流随时间变化

2.5 影响传热因素及其机理分析

计算过程中发现，势能分布与固-液界面的润湿性相关，故提取超亲水和超疏水两个工况下初始时刻的势能部分展示在图12中，为了对比明显，将标度统一到-0.12～0eV；统计壁面附近原子的数密度并将其记录在图13 中。可以看到润湿性较强的壁面的势能显著大于润湿性弱的壁面。同样壁面亲水性强会吸附更多的原子；凹半球纳米结构近壁面处的氩原子数密度更大，界面处更多的流体分子参与热传递会降低Kapitza 阻值，因此，亲水性凹槽里原子排布要密集，传热性质更优。在亲水表面上的凹半球纳米结构表面传热性能要优于其余两个表面；凸半球纳米结构表面的势能绝对值最小，但其接触面积相对平面更大，近壁面的数密度相对平面仍占据优势，所以凸半球纳米结构表面的传热性能也超过了光滑平面。而对于疏水壁面，因其势能较小，壁面附近原子更容易挣脱束缚，导致可进行热传递的原子数量减少，因而疏水表面热阻大，传热效果差。

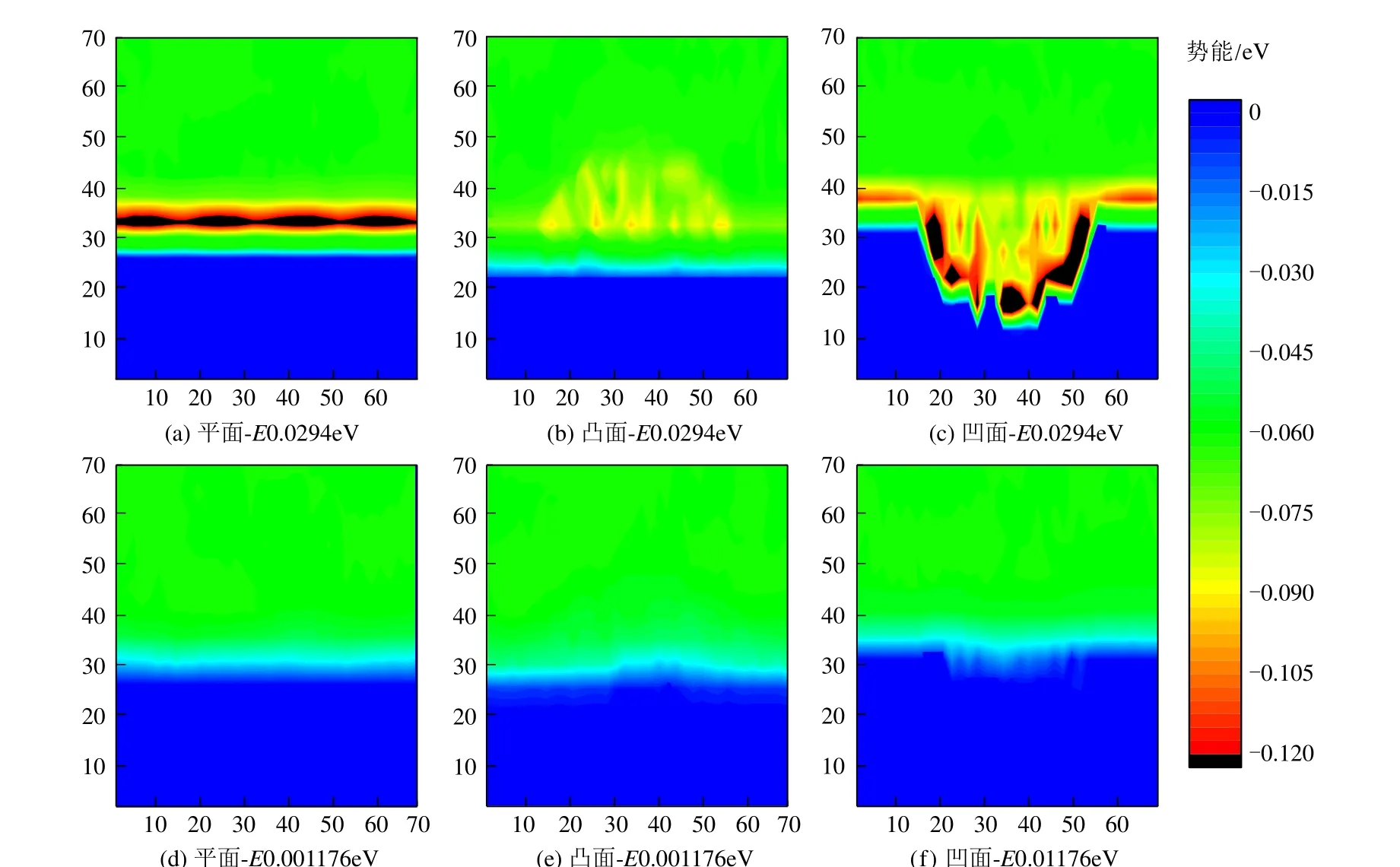
图12 初始阶段势能分布

图13 初始阶段密度分布

图14 展示了出现气泡时的温度随着接触角的变化趋势。图14(a)中温度指的是出现气泡时的壁面温度，可以看到，随着浸润性的增强，在接触角小于150°内气泡产生的温度呈上升趋势，说明接触角小即润湿性强的固-液表面气泡产生时间要短，这与模拟文献是一致的，这个微观结论与宏观上“疏水表面容易产生气泡”的结论正好相反，宏观上连续介质理论不能简单应用于微尺度系统，在微尺度系统中，宏观上可以忽略的界面热阻，在微纳尺度变得不可忽略，因此使用温度阶跃对气泡出现的温度进行了修正，当考虑固-液界面热阻时，气泡产生的温度与接触角的关系表示在图14(b)中，其展现出与图14(a)相反的趋势，即疏水壁面出现气体层需要的过热度反而更低，这与前人的实验结果相符。也就是说，在考虑温度阶跃和界面热阻的情况下，微尺度模拟结果与宏观实验本质上是一样的，疏水表面形成气泡并发生沸腾现象需要的温度更低。亲水表面固-液相互作用较强，拖延气泡出现，但是其较强的传热性能，传递给液体较多的热量，加速了气泡产生，而疏水表面固-液相互作用较弱，可促进气泡产生，传热性能却较差，气泡产生是两种作用相互博弈的结果，因微纳尺度上界面热阻不容忽略，导致与宏观现象的不同。

图14 出现气泡时的温度随着接触角的变化

3 结论

采用分子动力学方法模拟计算了不同润湿性平面和含凹、凸半球纳米结构三种表面上液氩层的池沸腾传热过程，分析了气相原子数、氩膜层温度、热流密度等参数的变化，通过固-液势能和接触角随温度变化分析亲疏表面产生气泡的机理，得到以下结论。

（1）平面和含凹、凸半球纳米结构三种表面在亲水工况下，液氩层的池沸腾传热过程可以明显分为两个阶段，即起始沸腾时间前后，表现为固-液分离前的加热和固-液分离后的加热沸腾过程，含凹半球纳米结构表面上起始沸腾时间、气相原子数、温升最高点及热流密度均大于相同润湿性条件的含凸半球纳米结构表面，两种微结构表面均大于平面情况。

（2）对疏水表面上微结构的影响不同于亲水表面，固-液间润湿性差，微结构的存在反而影响传热，起始沸腾时间延后，气相原子数减少，温升和热流密度降低，甚至在超疏水工况出现平面上液膜温升及热流密度均大于微结构表面的情况。

（3）从固-液作用势能和界面热阻讨论了微纳尺度亲疏水表面的微结构沸腾气泡产生的机理，亲水表面上固-液相互作用强，但是固-液间界面热阻小，而疏水及超疏水工况由于固-液相互作用小，固-液界面有空腔，造成界面热阻大，传热性能差，产生气泡晚于亲水表面。