机器学习在深冲钢质量自动判级中的应用

徐 钢，黎 敏，徐金梧

1) 北京科技大学钢铁共性技术协同创新中心，北京 100083 2) 苏州宝联重工有限公司，苏州 215131

流程工业，如冶金、化工等工业领域，产品在制造过程中涉及多个连续衔接的工序，为了确保成品的最终质量，要求每道工序的工艺参数设定在工艺规范所确定的区间内. 目前，企业对产品质量管控的主要手段是通过制订合适的工艺规范，并采用“事后”抽样检测方式来判定产品的品质.但是，这种依赖于生产经验制订的工艺规范及“事后”抽检的方式容易出现批量的产品质量判废，或导致用户由于质量异议提出索赔和退货. 中国钢铁企业每年仅质量判废和质量异议所造成的经济损失就近百亿元. 因此，如何利用大数据分析和人工智能方法，实现产品质量在线自动判级，提高产品质量可靠性是当前企业亟待解决的关键问题.

以大数据分析、人工智能、物联网+、云计算为代表的新一代信息化技术已经成为企业突破增长极限、保持稳定发展的重要途径[1-2]. 随着“工业4.0”时代的来临，制造技术正逐步从自动化、数字化、网络化向智能化方向发展. 作为工业4.0的重要策略—信息物理系统（Cyber-physical system,CPS）[3-5]，由于其具有自主判断、自主决策、自主调控的能力，将CPS的核心技术—数字孪生模型，应用于流程工业的智能制造引起了业内的高度关注[6-8]. 如何从海量的高维数据中提取出有价值的信息和知识是目前机器学习、人工智能、大数据分析、数字孪生模型等主要研究课题[9-11].

由于工业生产数据中往往具有多元、强耦合、非线性的特征，因此在建立产品质量数字孪生模型时存在一些问题[12-13]. 本质上，产品质量数字孪生模型是建立工艺装备所设定的工艺参数与产品质量指标之间的对应关系[14-16]，并根据各工序的实际工艺参数值来预测产品质量指标区间，实现产品质量在线智能判级和质量持续优化[17-19]. 目前，主要采用多元回归模型来建立质量预测模型，包括偏最小二乘法、神经元网络等回归方法. 近年来，机器学习方法已广泛应用于材料加工和材料研发领域[20-24]. 卷积神经网络（CNN）、循环神经网络（RNN）和图神经网络（GNN）等深度学习方法也用于材料研发和工业应用[25-28].

针对钢铁企业在产品质量在线自动判级中存在的问题，提出了基于高维数据非线性同等缩放与核简支集类边界计算相结合的机器学习方法，实现大类钢种的质量在线智能分类和自动判级.通过IF钢中三类钢种的样本数据进行验证结果分析，证实方法的有效性和实时性.

1 质量在线智能判级方法

质量在线智能判级方法是通过建立工艺参数与质量指标间的数字孪生模型，实现质量在线智能判级. 主要包括3个部分：（1）从实际生产线上，收集不同类别样本的工艺参数及对应的质量指标数据，并对训练样本的工艺参数进行聚类，形成低维的聚类映射图；（2）对不同工艺参数类所对应的质量指标进行分类，确定类边界并验证分类的准确性，然后建立工艺参数与质量指标间的数字孪生模型；（3）通过孪生模型将待判级样本的工艺参数映射到已建立的低维聚类图中，寻找若干邻近点的类别和预测的质量指标值来确定待检样本的所属类，实现产品质量的在线智能判级.

1.1 非线性同等缩放的聚类算法

在实际生产数据中，工艺参数、质量指标间往往存在多重耦合，变量间的非线性特征不可避免.近来年，基于核方法的非线性模式分析算法受到关注. 核方法是通过非线性核函数来表示数据内在的非线性结构特征，其中高斯核是核函数中最常用的表达形式. 为了揭示高维数据中内在的非线性低维的潜在结构，需要在高维数据空间中嵌入一个低维的子空间，并将样本数据映射到低维子空间来观察数据内在的结构特征，这种方法也称为数据可视化[6,29]. 数据可视化的目的是通过高维数据的多维缩放算法将数据映射到2D或3D空间，并保持原始数据结构的基本特征不变.

经典的降维算法，如主成分分析（Principal components analysis，PCA）和核主成分分析（Kernel principal components analysis，KPCA）在模式分析中已被广泛应用[30-31]. PCA是通过从协方差矩阵中提取最大的几个特征向量组成的单位主方向，并将数据映射到互相正交的主方向上，从而构成低维的数据主成分. KPCA是从核内积矩阵中求核主方向，计算特征空间中样本点在核主方向上的投影，实现数据低维可视化，并消除数据噪声和非线性耦合. 由于核方法能更好的表示非线性特征，所以KPCA的多维缩放在处理复杂的数据结构时具有一定的优势. 无论PCA、还是KPCA，从概念上是将数据在低维子空间的表示形式与原始空间中数据之间残差的范数平方和最小化. 但是，这种通过这类高维数据进行缩放方法，容易造成复杂高维数据的内在结构特征在降维后出现畸变.

为了解决非线性数据在降维后易出现畸变问题，提出了新的数据降维方法. 该方法将特征空间的样本点间的平方距离与投影到低维子空间的平方距离的相关性最大化来实现非线性多维缩放. 新方法在对非线性数据多维同等缩放(Multidimensional parity scaling, MDPS)过程中，最大程度地使原始空间中的样本点之间的距离与经过2D或3D缩放后样本点之间的距离保持同等缩放.

式（7）的解可由拉普拉斯矩阵L(K)的特征值分解中求得，其中为矩阵L(K)的特征向量. 由前两个最大特征值所张成的特征向量子空间可以实现高维数据的2D 缩放. 高维数据经非线性同等缩放后的效果，将在下一章节中讨论.

1.2 核简支集分类算法

实现产品质量在线判级需要建立工艺参数与质量指标之间映射关系，根据工艺参数聚类结果确定类标记，并对带有标记的质量指标样本划定类边界. 分类方法有基于概率分布的Bayes算法、Anderson算法；基于规则的决策树，如随机森林和Boosted树；基于距离的支持向量机、K-邻近分类以及二次规划分类、逻辑回归以及神经元网络、深度学习等.

基于距离的分类算法可分为两种形式，硬间隔和软间隔分类算法. 硬间隔分类采用线性（超平面）判别函数，软间隔采用非线性（曲面）判别函数[29].由于工艺参数与质量指标间存在多重耦合，类边界往往较复杂，因此宜用非线性判别函数，即采用软间隔分类器. 引入间隔松弛向量，即允许训练集中个别样本被错误分类，软间隔支持向量机分类方法可转化为求如下最优解

为了简化类边界判定函数，提出通过少量简支集（Reduced set，RS）来确定类边界判定函数的方法. 设为支持向量集，nsv为支持向量个数，则基于支持向量的类判别函数

式中，σ为核函数参数，nn表示参与学习的部分支持向量个数. 由于简支集分布在类边界曲线（或曲面）上，因此可以实现正确、快捷的类判别. 上面所讨论的利用简支集确定类边界的方法可简化质量自动判别的过程，并为不同钢种的工艺规范的制定提供依据，具体应用在下面章节中讨论.

为了验证方法的有效性，下面讨论应用实例.数据取自两个不同类的数据，由于类间数据交叉重叠，因此类边界较复杂，且支持向量较多. 为了合理划分类边界，首先采用软间隔支持向量机，求出76个支持向量，如图1所示. 然后，取简支集的个数为10，从支持向量集中随机抽取部分支持向量组成 10个子集，通过式（11）和式（12），求出各子集的简支集优化解. 最后，通过函数拟合方法求得类边界曲线，如图1所示.

图1 利用简支集确定类边界的例子Fig.1 Example of determining class boundaries using reduced sets

1.3 质量在线评级与质量指标预测

实现产品质量在线智能判级，首先需将待判样本通过同等缩放后投影到经过训练的工艺参数聚类图上，并根据映射点的位置选取距该点最近的K个训练集中的样本点作为参考样本集. 然后，从质量指标分类图中找出这些参考样本集的类属性，采用K-邻近分类法（KNN）确定待判样本的类别. KNN算法的核心是，一个样本在特征空间中的K个邻近样本（参考样本）中的大多数属于某一个类别，则认为该样本也属于这一类别. 由于KNN方法对类域存在交叉、重叠的待分样本集来说具有快捷、准确分类的特点，因此这种方法可以实现产品质量的在线快速判级.

此外，还可以通过非线性回归模型，如核偏最小二乘法、神经元网络、深度学习等方法预测待测样本的产品质量指标值，并根据2.2节中讨论的产品质量指标的类边界，利用综合判定的方法来判定待测样本的产品质量类别.

基于机器学习的产品质量自动判级过程，包括以下4个步骤：

（1） 数据采集与预处理：从实际生产线上采集主要工序的工艺参数和质量指标数据，并对样本集中的数据进行清洗，剔除数据集中缺失数据、异常点等不规范数据；

（2） 工艺参数聚类分析：将采集的高维工艺参数采用多维同等缩放方法映射到低维空间中，通过软间隔支持向量机实现工艺参数的低维空间的聚类并优化模型参数；

（3） 确定不同类的边界：将样本的质量指标值映射到质量分布图上，利用简支集分类器确定类边界（不同产品类的边界），并根据边界曲线划定不同类的上、下限；

（4） 在线判级和性能预测：将待判样本的工艺参数通过同等缩放投影到低维映射图中，并选取邻近的K个训练集中的样本点作为参考样本，采用K-邻近分类法确定待判样本的类别；通过核回归、BP网络、LSTM网络（Long short-team memory）等方法预测产品质量指标值，并结合预测值进行综合判定.

图2给出了基于机器学习的产品质量自动判级过程的流程图. 在下章节中，将讨论质量在线智能判级和质量指标预测方法的工业应用实例.

图2 产品质量自动判级流程Fig.2 Workflow for automatic discrimination of product quality

2 工业应用实例

下面以汽车用钢为例，讨论运用机器学习方法实现产品质量在线判级，以避免发生批量的质量判废. 汽车制造过程中，需要用到不同种类的钢材，其中主要构件的原料是深冲钢（IF钢）. 这类钢种属同一大类钢种，其制造工艺和过程参数基本一致，主要通过调整部分工艺参数，制造不同性能的钢种. 深冲钢在成形与使用中需考虑其冲压性能、力学强度、抗冲击性能等质量要求. 主要力学性能指标包括：屈服强度、抗拉强度、延伸率和塑性应变比等. 深冲钢生产过程中主要涉及炼钢、热轧、冷轧和热处理等工序，不同工序需严格控制相应的工艺参数才能制造出客户所要求的产品质量. 炼钢工序应控制冶炼过程中钢坯的主要成分：C、Mn、P、S等元素的质量分数；热轧工序：加热炉出口温度、精轧入口温度、精轧出口温度、卷取温度等；冷轧工序：冷轧压下率；热处理工序：加热平均温度、均热平均温度、快冷出口温度、时效出口温度、缓冷出口温度等.

为了分析不同等级汽车钢板在各制造过程中工艺参数的分布规律，从某钢铁企业实际生产线上获取深冲钢系列的DC04、DC05和DC06 三种牌号的汽车钢生产数据. 主要成分和工艺参数名称及统计量如表1所示.

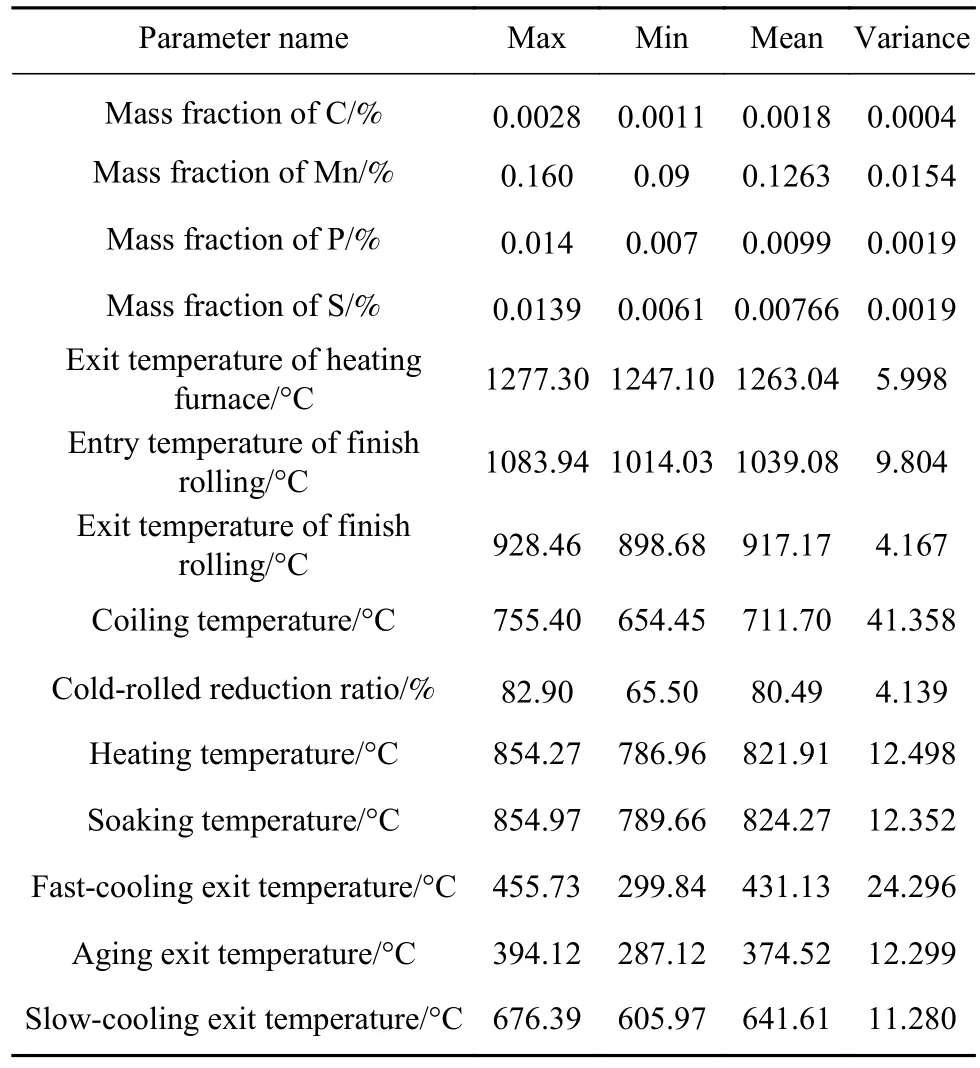
表1 主要工艺参数名称及统计值Table1 Major process parameters and statistics

三种牌号汽车钢的主要性能指标的行业标准如表2所示，包括：屈服强度、抗拉强度、延伸率、塑性应变比等. 通常，企业为了提高产品的市场竞争力，往往制定比行业标准更为严格的企业内部质量标准，如某钢铁企业内部标准也在表2中给出. 下面按照上一章节所提出的方法，讨论具体计算过程和分析结果.

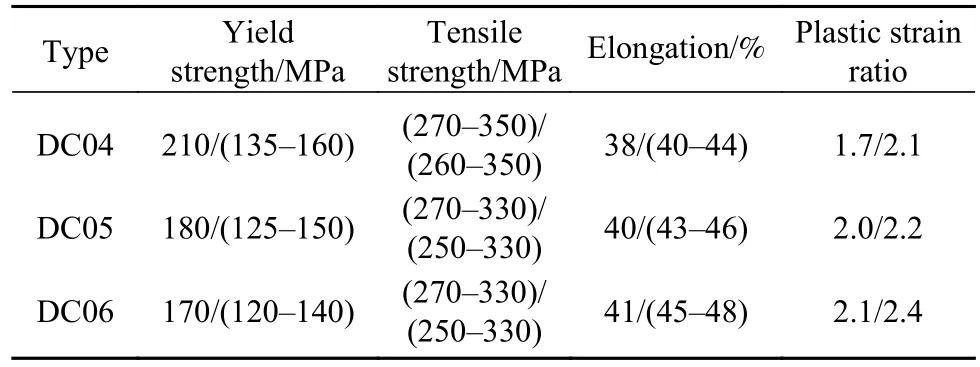
表2 汽车钢性能指标的行标/企业内标Table2 Industry/internal standard of performance index of interstitialfree steel

2.1 数据采集与清洗

从实际生产线上采集三种牌号深冲钢的269个工艺参数和质量指标值. 原始数据集中有24个工艺参数，其中10个工艺参数与产品力学性能无直接关系，因此选择14个相关的参数作为学习样本集，其工艺参数的统计值已在表1中列出.对工艺参数与质量指标作相关分析，发现14个变量中只有8个变量的相关系数的绝对值较大，其他变量的相关系数的绝对值均小于0.3. 相关系数低的原因，（1）该变量与质量指标间没有明显的关联；（2）该工艺参数方差很小，对质量指标不会造成影响，如元素S和P质量分数，加热炉出口温度等没有明显变化. 选出的8个关键工艺参数包括，炼钢工序：C、Mn质量分数；热轧工序：精轧入口温度、精轧出口温度、卷取温度；冷轧工序：冷轧压下率；热处理工序：快冷出口温度、缓冷出口温度.

除了选择关键变量外，还需要对样本集中的数据进行清洗，剔除训练样本中存在缺失数据、异常点等不规范的数据. 采用常用的统计分析方法，对269个样本集进行清洗后，发现其中有21个样本点存在数据缺失，因此剔除这21个样本点，只保留248个样本作为训练样本.

2.2 工艺参数聚类分析

为了揭示高维、多重耦合的工艺参数中内在的分布特征，需将高维数据映射到低维子空间来观察数据内在的结构特征，这种方法也称为数据可视化. 分别采用PCA、KPCA和非线性多维同等缩放算法（MDPS），对248个高维的训练样本数据进行降维，并对二维数据进行聚类，分析不同降维算法的效果和聚类精度.

首先，需优化非线性多维同等缩放算法的核参数，图3给出了径向基核参数σ在0.1～6.0之间所对应的累积误差. 由于L(K)矩阵具有半正定特征，对应的特征值，所以累积误差为负值. 从图3中可以看出，当核参数σ取2.0时累积误差最小. 图4分别给出两种不同方法降维后，2D的映射图及聚类的结果. 为了便于比较，这两种方法均将选出的8个关键变量经标准化处理后，提取4个特征向量，并将其中特征值最大的2个特征向量作为2D数据的主成分轴.

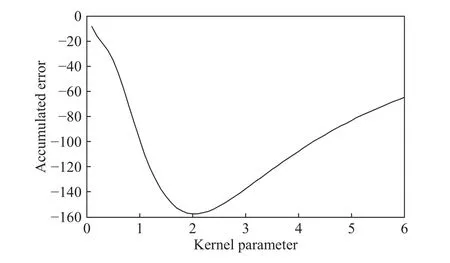
图3 核参数取不同值时累积误差分布图Fig.3 Accumulated error with different Kernel parameters

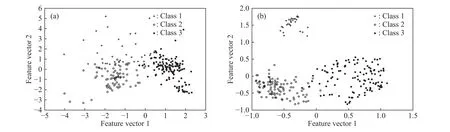
图4 线性PCA方法(a)和非线性多维同等缩放方法(b)降维后的工艺参数聚类图Fig.4 Parameter distribution after reduction using PCA (a) and MDPS (b)

从图4中可以看出，采用线性PCA方法的聚类图中（图4(a)）不同工艺参数的类边界存在较大的重叠区域，且同一类数据分布较为分散，这将造成质量判级时误判. 采用非线性同等缩放方法获得的聚类图中（图4(b)），3类工艺参数的类边界清晰可分，类内样本相对集中. 表3给出了用3种不同降维方法(PCA、KPCA和MDPS)并对降维数据进行K-均值聚类，关键工艺参数的类均值和类内样本方差.

表3 三种方法工艺参数类中心/类内方差数据Table3 Class center/ mean square error of quality indexes using three methods

对不同类的训练样本的质量指标值的类间距离及类内方差数据进行对比分析，说明了非线性同等缩放降维方法优于线性PCA和非线性KPCA方法，且与表2中给出的IF钢的质量指标分类标准基本上一致. 通过这个实例分析说明，选择合适的聚类方法（如非线性同等缩放的聚类方法）对工艺参数进行聚类，属同一类的工艺参数与其所属类的质量指标有密切的对应关系. 通常，机器学习方法在工业中的应用，其主要目的是建立工艺参数与质量指标间的映射关系，即建立工艺参数-产品质量间的数字孪生模型，并通过数字孪生模型对产品质量实现在线管控.

从表3中可以看出，类1与DC06，类2与DC05，类3与DC04钢种相对应. 另外，从表3中还可以看出，所有训练样本的抗拉强度、塑性应变比这两个指标都在行业和企业内标要求范围，但延伸率、屈服强度对不同牌号有较大差异.

2.3 产品质量在线判级和性能预测

质量在线智能判级需建立工艺参数与质量指标之间映射关系. 首先，对工艺参数进行聚类，确定每个训练样本的类别，并给出训练样本的分类标记. 然后，将标记样本的质量指标值映射到质量分布图上，并根据样本的标记类别划定不同产品类的边界. 图5给出了248个训练样本中，采用2.2节给出的非线性同等缩放降维和K-均值聚类后，标记样本的质量指标分布图. 由于抗拉强度、塑性应变比这两个指标所有样本均满足质量标准要求，因此在图5中仅给出延伸率、屈服强度的质量指标分布情况. 在获得质量分布图后，可以采用式（8）的软间隔支持向量机求出类边缘的支持向量集. 然后，由式（12）给出简支集分类器所确定的类边界.

为了便于实际工业应用，将图5中曲线边界简化为线性（矩形）边界，如图6所示. 在图6中，质量分布的类边界线划定了不同类的质量指标上下限. 如果将工艺参数确定的质量类别与钢种标准确定的类别作对比，可以看出：类1（钢种DC06）延伸率的下限为45%，屈服强度的上限为135 MPa；类2（钢种DC05）延伸率的下限为43%，屈服强度的上限为145 MPa；类3（钢种DC04）延伸率的下限为40%，屈服强度的上限为160 MPa. 对照表2给出的汽车钢企业内部标准，上述方法所确定的上下限与表2的内部标准是一致的. 唯一的差异是DC06和DC05这两类钢种的屈服强度的上限减少5 MPa，这比企业制定的内标还要严格，以确保产品质量的合格率. 但是，有7个属于类型2的样本在DC05控制限外（如图6所示），因此视为错误分类，整体分类的准确率为97.2%. 需要说明，由于钢种的质量标准上下限原因，如DC04的屈服强度范围为 135～160 MPa，DC05的屈服强度范围为125～150 MPa，因此类1和类 2的样本在DC04和DC05存在重叠区域，但这并不表明由工艺参数所确定的类被误判. 如，DC04中的个别样本点落在DC05区域，可以被判定为DC05，因为这些样本满足DC05质量指标，同样这些样本也满足DC04质量标准，因此不会引起客户异议.

图5 标记样本的质量指标分布图Fig.5 Quality index distribution of labeled samples

为了检验在线自动判级的准确性，表4给出采用不同判级和性能预测方法的计算结果. 采用如下6种方法.

表4 不同判级和性能预测方法的计算结果Table4 Calculating results of discrimination and predicting qualityindex using different methods

（1） BP网络：数据经过标准化处理后，输入到BP网络，网络输入层为8个变量（工艺参数），隐含层20个节点，输出层为4个变量（质量指标），预测质量指标值，并根据预测值对标图6的上、下限范围对待测样本进行判级；

图6 三种钢种的质量指标的上下限Fig.6 Up and down limits of quality indexes for three steel types

（2） 长短时记忆网络（LSTM）：LSTM 网络主要用于序列数据的预测和分类，本案例中采用遗忘门、输入门、输出门以及2层隐含层和32个隐含节点建立全连接网络，通过预测质量指标值，并根据预测值和质量指标的范围对待测样本进行判级；

（3） 核偏最小二乘法（KPLS）：采用高斯核函数，通过非线性降维，取4个主成分，建立回归方程来预测质量指标，并根据预测值和质量指标的范围对待测样本进行判级；

（4） 偏最小二乘法（PLS）：采用传统的线性降维方法，取4个主成分建立回归方程来预测质量指标值，并根据预测值对待测样本进行判级，过程与KPLS方法相似；

（5） KNN+统计平均法：工艺参数通过同等缩放投影到低维映射图中，并选取邻近的7个训练集中的参考样本，计算参考样本的质量指标的平均值来确定待测样本的类别；

（6） 综合分类法 (Synthesis)：通过对 LSTB、BP与KPLS、KNN四种方法所确定类别进行综合评判，将占多数的类别判定结果作为最终判定的类.

在这6种分级方法中，BP网络、LSTM、核偏最小二乘法、偏最小二乘法属于全域分类法，KNN+统计平均法属局域分类方法. 全域分类是根据质量参数的整个分布域，建立分类模型. 局域分类将类域划分为若干子域，根据子区域内样本的属性来确定待测样本的所属类，如“KNN+统计平均法”是采用K个最邻近样本的质量指标的统计平均值作为判据.

为了检验方法的有效性，从生产线另外采集100个样本的工艺参数与实测质量指标，通过前面给出的方法对待测样本进行判级，结果如表4所示. 从表4中可以看出，由于综合分类法集成了4种算法的各自优点，综合分类法的判级准确率为96%. 在4%的误差中，其中一半以上的错误判级是将合格的产品误判为不合格产品.

从表4还可以看出，采用非线性方法，如LSTM、BP网络和KPLS，不论性能预测精度（方差）和分类准确率均优于线性的PLS方法，表明对于高维、多重耦合的工业数据拟采用非线性分析方法. 另外，基于循环神经网络构架的LSTM网络考虑了序列数据之间前后关联，并具有记忆功能，解决了传统神经网络存在的先前学到的“信息丢失”问题，因此其质量指标的预测精度均优于其它方法. 虽然，LSTM方法具有很高的预测精度，但由于存在不同类的交叉边界和质量指标预测值的误差，仍会出现个别样本点的误判. 解决这类误判方法将在下一章节中讨论.

3 讨论和建议

（1） 训练样本集的筛选. 对于质量要求相近的大类钢种，产品制造过程的流程和工艺参数的设定也是相近的，因此不同级别的产品质量指标存在交叉重叠区域. 为了更精确地实现质量在线自动判级，需对训练样本进行筛选，剔除类间重叠区域的样本，并适当增加类边界的样本数量，可进一步提高自动判级的准确率.

（2） 存疑样本的终检. 采用综合分类法时，4种方法中有90%以上的判级结果是完全一致的，有10%左右的判级结果存在差异. 存在差异的样本集中在两类钢种的重叠区域，虽然通过综合判定法纠正了部分误判，但仍有4%左右被误判.建议对综合判定后存疑的5%～10%的样本标记为待检样本并进行事后终检，这样既避免盲目抽检，降低检化验成本和时间，同时提高判级的准确率.

（3） 优化生产工艺规范. 在2.3节中已讨论了利用简支集来确定类边界，图6给出了三类钢种的质量指标分类的上下限. 因此，类边界的简支集对应的样本数据可以用于不同钢种的工艺参数规范的制定，优化工艺规范，即根据这些简支集样本的工艺参数的来制定合适的工艺规范标准，严格按照规范要求组织生产，可进一步提高产品质量.

4 结论

本文结合流程制造业的特点，提出了利用机器学习实现产品质量在线自动判级方法. 工业应用实例证实，利用机器学方法能解决企业目前采用的“事后”抽检方式易引起的质量不合格问题，避免企业由于用户索赔造成重大的经济损失. 主要结论如下：

（1）针对工业生产数据中具有多元、强耦合、非线性的特点，提出了高维数据非线性同等缩放算法. 算法将特征空间的样本点间的平方距离与投影到低维子空间的平方距离的相关性最大化，实现高维复杂数据的可视化，并采用聚类分析来揭示不同产品等级所对应的工艺参数分布特征.

（2）提出了核简支集类边界确定方法. 根据工艺参数聚类结果，建立训练样本的质量指标分布图，通过软间隔支持向量机求出不同质量类边界的支持向量集，并由简支集分类器确定不同产品质量级别的类边界.

（3）提出了质量在线判级和质量指标预测方法. 通过汽车用钢（IF钢）的工业应用实例证实，应用机器学习方法在训练阶段的钢种在线判级的准确率为97%，在测试阶段的准确率为96%. 产品质量在线自动判级方法具有很高的效率，每个产品（钢卷）在普通台式机上自动判级所需时间不到0.1 s，完全可以满足产品在线自动判级要求.