基于CEL法的裙边桩靴插桩数值分析
2022-05-25王维刚袁峰超刘金梅
王维刚 袁峰超 刘金梅
(东北石油大学机械科学与工程学院)
自升式平台是油气行业中最常用的海上钻井平台之一,具有灵活、可重复使用的特点。 自升式平台由一个有浮力的船体和桁架桩腿组成。 桩腿是可伸缩的, 通过齿轮齿条系统进行垂直移动,并连接到桩靴底座上。 典型桩靴的有效直径可达20 m,常见的结构为纺锤形,结构的不同在很大程度上影响了桩靴的插桩阻力。 桩靴与海底土的相互作用,支持平台在服役期间安全站立。
自升式平台结构安全事故大多与地基失效密切相关,地基失效会导致桩腿突然下沉发生穿刺现象,进而导致平台毁坏。 国内外学者进行了大量桩土相互作用的研究工作,主要目的是获得插桩过程中桩靴的插桩阻力,即获得地基的承载能力。 研究方法主要有理论分析法、模型试验法和数值仿真方法[1]。
自升式平台最容易发生的失效模式为穿刺,准确预估平台在井位附近插桩的阻力有助于提前预判穿刺的可能性。 一旦在现场确定了穿刺事故的风险,就需要采取缓解措施,以确保自升式平台的安全安装。 按惯例,在安装程序方面采用逐条腿预压的方法已经被用于减轻穿刺或控制桩腿的穿刺。Tho K K等最先采用CEL法模拟自升式平台桩靴插桩过程[2]。Qiu G和Henke S采用CEL法研究了桩靴在均质粘土、砂土和成层土上的插桩过程, 并与离心机模型试验结果进行对比,证明了CEL法在插桩过程中的适用性[3]。但CEL法研究插桩过程还不够完善, 在建立数值模型时,需要合理设置相关参数,参数设置的不同对结果的影响很大。 裙边桩靴又称桶形桩靴,国外已经对裙边桩靴展开了一些研究,Byrne B W和Wardrop J对桶形桩靴和传统桩靴在固结粘土中承受复合载荷的能力进行对比试验[4,5]。张蒲阳和丁红岩采取塑性分析方法,比较了桶形桩靴和传统型桩靴的不同载荷性能,表明桶裙结构可以加大桩靴的入泥深度,也即增强平台的安全性能,但未探讨裙边长度对插桩阻力的影响[6]。
综上所述, 笔者运用CEL法模拟裙边桩靴在上硬下软双层粘土中的插桩过程,并研究不同插桩深度下土体的流动规律、 插桩阻力-深度的关系和裙边桩靴裙长对插桩阻力的影响。
1 桩靴插桩数值建模
由于需要模拟桩靴的连续贯入过程和插桩过程导致的土体流动变形,因此笔者运用有限元程序ABAQUS/Explicit模块进行插桩分析, 借助CEL法计算技术开展研究。
1.1 模型建立
目标自升式平台桩靴是在传统纺锤形桩靴的基础上改进得来的, 纺锤形桩靴与裙边桩靴的几何尺寸如图1所示(单位mm),桩靴最大承载面积为28.26 m2,两种桩靴插桩几何模型如图2所示。

图1 自升式平台桩靴几何尺寸

图2 桩靴插桩几何模型
裙边桩靴的设计方法是在最大承载面以下加上一圈裙边, 裙边长度L根据桩靴直径D变化,变化范围为(0.0~0.5)D,但保持裙边厚度在一个标 准 范 围(0.001~0.010)D 之 内[7],取 其 大 小 为0.008D。 数值仿真分析主要研究桩靴入泥深度和插桩阻力之间的关系,并不关心桩靴的结构变形, 况且桩靴结构相对于土体基本不发生变形,故可约束为刚体。 约束其参考点的所有自由度,在插桩分析步中释放参考点竖直向下的约束,赋予15 m位移,分析步时间设置为75 s,即加载速度为0.2 m/s,在显示动力学分析中,加载速度过快会导致结果振荡,这个加载速度被证明足以缓慢消除动力效应产生的影响[8],因此选择0.2 m/s的加载速度模拟自升式平台桩靴入泥动态过程。 整个模型只需要定义1个土体重力载荷。
1.2 参数选取
采用有限元方法模拟自升式平台桩靴插桩时,理想弹塑性模型可以描述土体的应力应变关系,遵循摩尔-库仑强度准则。 在有限元数值模拟中,若未指定等效塑性应变,ABAQUS认为粘聚力保持不变,即为理想线弹塑性模型。 理想线弹塑性模型有粘聚力、弹性模量、泊松比、摩擦角和剪胀角这5个基本参数。 采用文献[9]中的土工离心模型试验所采用的土体参数进行模拟。 上部硬土层土体重度为8.03 kN/m3,不排水抗剪强度为38.3 kPa,厚度与桩靴直径相等。 下部软土层土体重度为7.00 kN/m3, 不排水抗剪强度为12.0 kPa,若土体为不排水粘土,则泊松比取为0.49,对粘土的弹性模量取值参照表1, 内摩擦角取一小值φ=0.01,剪胀角ψ=0°。 桩靴的材料属性为:弹性模量E=205 GPa,泊松比μ=0.3,密度ρ=7800 kg/m3。

表1 饱和粘土弹性模量取值
1.3 土体范围选取及网格划分
土体地基径向和深度方向的尺寸规格选为6D×8D,将土体以上留出一个空穴层,赋予空的材料属性,给土体的隆起提供空间,空穴层高度在数值上等于桩靴直径。 桩靴采用三维六面体减缩积分单元C3D8R 模拟, 土体采用欧拉单元EC3D8R模拟。 网格尺寸的选取对数值计算的精确度影响较大,本次计算中,与桩靴表面接触的土体受力变形相对较大,采用细密网格;远离桩靴的土体受力变形相对较小,采用稀疏网格。CEL法的计算速度主要与稳定时间增量Δt相关,Δt为:

式中 cd——膨胀波波速;
E——材料的弹性模量;
Lmin——最小网格单元尺寸;
Δtcrit——临界时间增量;
ρ——材料密度。
由式(1)可知,要想加快计算时间、降低计算成本,可以增大最小网格单元的尺寸、增大材料弹性模量、降低材料密度,因此在划分网格时要保证网格划分的均匀且最小网格单元最大。 在兼顾计算精度与计算时间的同时选取合适的网格尺寸。 由文献[10]的结论可知,细密网格范围取2D,大小取0.05D,稀疏网格大小取0.10D。
1.4 边界条件及初始地应力平衡
对桩土数值模型进行约束时,在水平边界上施加竖直方向的速度约束,在竖直边界上施加水平方向的速度约束,并设置欧拉吸收边界来消除由计算模型尺寸选取不当导致的边界效应,减小计算结果的振荡。
由于有限元仿真模型采用显示动力学分析,因此采用关键字定义初始地应力的方法来平衡地应力。 建立好有限元模型之后,分别测量出硬土和软土区域最高点和最低点坐标,并通过自重应力公式分别计算出坐标对应的土体自重应力值。 在新版ABAQUS中, 在Load模块下执行Creat Predefined Field命令, 选择Mechanical下的Geostatic Stress对模型施加初始地应力。对均匀地质,在地面下z深度处的垂直应力σz=γ0z[11],其中γ0为土体有效重度。 在自重条件下,有σx=σy=K0σz,其中K0为静止侧压力系数,0≤K0≤1。 K0比较难测出,根据经验K0取值为1。
1.5 接触设置
土体和桩靴底部、侧面的接触采用通用接触算法。 如今,大部分研究者将插桩过程中桩土间的接触类型简化为完全光滑或完全粗糙接触,这两种情况下的插桩阻力最大相差5%,且对土体流动过程几乎没有影响。 因此,笔者假定桩靴表面光滑,桩土之间无摩擦,即将接触属性定义为空,保持默认设置。
2 结果分析与讨论
置于上硬下软层状粘土地基的自升式平台,若上下土层强度相差较大,随着桩靴在地层中所处深度的逐渐增加, 当贯入深度超过某一数值时,承载力将发生急剧变化引起桩靴突然下沉发生穿刺现象,严重的将导致桩腿和升降系统的结构破坏和平台的完全失效。 因此探讨采用裙边桩靴来减轻穿刺带来的危害,对裙边桩靴插桩的承载力变化规律进行研究,并探讨了裙长对插桩阻力的影响,给出最优的裙长。
2.1 裙边桩靴插桩地基承载力性能评价
大多数穿刺事故在上硬下软层状土体条件下发生。 通常,在安装过程中通过采用逐条腿预压的方法来减轻穿刺破坏或控制桩腿穿刺。 为探究采用裙边桩靴进行插桩时的情况,绘制桩靴位移与插桩阻力的关系曲线。 如图3所示为裙边桩靴与纺锤形桩靴插桩阻力-深度曲线的对比,随着插桩深度的增加,承载力在持续增大,在快到达双层土交界面时,承载力出现波动,穿过硬土层后,插桩阻力继续上升,最终达到极限,然后下降。 通过对比可知,采用裙边桩靴进行插桩时,所受的插桩阻力比纺锤形桩靴所受到的小,因此采用裙边桩靴能够减轻穿刺危险。

图3 裙边桩靴与纺锤形桩靴插桩阻力-深度曲线
2.2 数值模型结果验证
当桩靴基础在上硬下软双层均质粘土中插桩时, 可采用ISO 19905.1—2016规范中推荐的Meyerhof(1969)公式来计算桩靴的插桩阻力Qv,即:

式中 A——桩靴有效承载面积;
D——桩靴最大直径;
d——桩靴入泥深度(插桩深度);
dc——承载力深度系数;
H——桩靴到下部软粘土层的距离;
NcSc——承载力系数,对于圆形桩靴,其值为6;
p′o——深度为D时覆盖土层压力;
Su,b——下部软粘土层的不排水抗剪强度;
Su,t——上部硬粘土层的不排水抗剪强度;
γ′——深度d以上粘土的平均有效重度。
当插桩深度为5 m时, 将各参数代入式(1),得到地基的插桩阻力为2.9 MN。 由图3可知,插桩阻力为3.1 MN,与式(1)的计算结果相比,误差为6.4%, 说明所建立的插桩数值模型符合实际情况,结果具有一定的可靠度。 另外,通过与文献[12]中离心机试验的结果进行对比,更进一步说明该模型是可靠的。
2.3 裙长对土体承载力的影响分析
选取不同的裙边长度L(0.15D、0.20D、0.25D、0.30D) 来研究在插桩过程中其对插桩阻力的影响,所得插桩阻力-深度曲线如图4所示。

图4 不同裙边长度的桩靴与纺锤形桩靴插桩阻力-深度曲线
由图4可知,当桩靴刚开始贯入硬土层时,不同裙边长度计算得出的插桩阻力随着平台贯入深度的增加而迅速增大,且变化趋势平缓。 其中,在桩靴临近土层分界面之前,插桩阻力出现些许波动,主要是因为下部软土层慢慢开始持力。 在上部硬土层约3 m处的位置,插桩阻力发生突降,并将这一趋势一直保持到桩靴接近软土层,当桩靴进入软土层之后插桩阻力持续增大。 到达9 m左右,插桩阻力达到最大值并迅速下降。 纺锤形桩靴在9 m左右位置会因为插桩阻力突降发生穿刺现象。 由图4还可看出,在逐渐增大裙长的情况下,承载力突然减小的现象逐渐变弱,当裙长L=0.25D时,插桩阻力较平顺,此时不易发生穿刺现象。 但随着裙长继续增大,达到0.30D时,承载力变化虽然较平顺,但插桩阻力也相应减小,不利于平台站立。 由此可知,当裙长L=0.25D时,插桩阻力最大(即土体承载力最大),且不易发生穿刺现象。
2.4 不同插桩深度土体流动规律
土体的流动规律会严重影响插桩阻力的大小,因为桩靴贯入深度较大时,桩靴周围的土体会发生坍塌回流, 坍塌的土体覆盖在桩靴上部,它的重力会进一步增加插桩深度。 图5、6分别为纺锤形桩靴与裙边桩靴不同插桩深度下的土体变形图,中间红色部分为硬土层,硬土层的上、下层分别为空穴层和软土层。
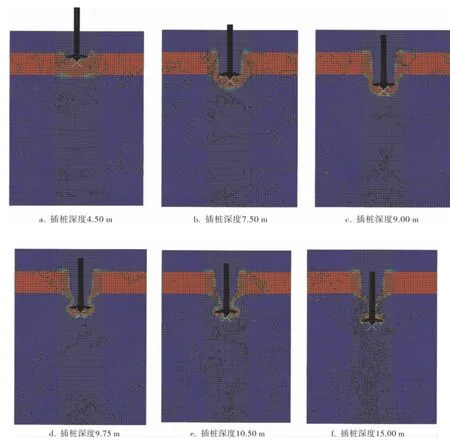
图5 纺锤形桩靴不同插桩深度下的土体变形图

图6 裙边桩靴不同插桩深度下的土体变形图
由图5、6可知,桩靴在插桩过程中,土体通常会经过以下几个阶段的流动:在桩靴贯入土层之初,桩靴下的土体开始流动,硬土层表面发生隆起,桩靴周围形成一个小的桩坑,桩坑的大小随着插桩深度的增加而增大; 随着桩靴的继续贯入,桩靴下的土体开始向上流动,并逐渐越过桩靴表面发生回流现象;随着桩靴进一步贯入软土层中, 由于软土层土体不排水抗剪强度很小,桩靴下部的硬土被压入软土中,而没有向上流动的趋势;随着桩靴继续贯入,桩坑变小,最后达到一个稳定值;当桩靴完全贯入土体时,桩靴上部土体形成一层密封层,阻止了壁面土体流动,但桩靴周围的土体仍然沿着其边缘流动,称为“局部流动”。 因此,当桩靴插桩深度比较浅时,土体失效模式为一般剪切失效; 随着插桩深度的增加,土体的失效模式会变得越来越复杂,故采用理论分析法无法评估实际工程中的自升式平台桩靴插桩性能。
插桩时,相较于纺锤形桩靴,裙边桩靴底部会压入大量的硬土, 这部分硬土在下方持力,会使得桩靴贯入阻力更平顺, 减轻阻力突变的情况, 因此采用裙边桩靴可以减小穿刺带来的危害。
3 结论
3.1 对于上硬下软层状地基,采用裙边桩靴能够减小桩靴贯入土体时的插桩阻力,随着裙边长度的增加,插桩阻力变得越来越平顺,且当裙边长度L=0.25D时,插桩阻力最平顺,此时的插桩阻力相对较大。
3.2 观察裙边桩靴插桩过程中土体的流动规律可知,与纺锤形桩靴相比,裙边桩靴会将大量的硬土压入软土层, 使得桩靴贯入阻力更平顺,减轻阻力突变的情况,采用裙边桩靴可以减小穿刺带来的危害。
