机载双基地雷达空时二维杂波建模与特性分析
2022-05-24武亚涛孙清洋刘云申
胡 滨,何 强,武亚涛,孙清洋,刘云申
(南京电子技术研究所,江苏南京 210039)
0 引言
随着隐形武器、电子干扰和反辐射导弹等新型武器装备的迅猛发展以及先进战术体系的不断升级,双基地雷达系统在现代战争中的优势日趋明显。相比于传统的单基地雷达,双基地雷达通过收发分置的工作方式,可将价值高昂的发射机置于远离战场的位置,而将接收机前出到敌方区域,这种探测体制具有作用距离远、抗干扰能力强、安全性高、反隐身、易于扩展等诸多优点。
然而,机载双基地雷达通常工作于下视状态,在动目标探测过程中,面临强杂波的影响,微弱目标回波可能会被淹没在杂波背景中而无法被检测到。并且机载双基地雷达杂波特性比单基地雷达杂波特性更加复杂,其空时二维分布特性与双基几何构型参数(收发平台的载机速度、飞行高度、阵面轴线与飞行方向以及双基基线的夹角等)相关,加剧了杂波分布的不规则性和距离非平稳性,进一步增加了杂波抑制的难度。因此,构建准确的机载双基地雷达杂波模型并深入探讨杂波空时分布的一般性规律,可为后续开展双基地机载雷达系统杂波抑制的研究工作提供理论支撑和应用基础。
目前,海内外学者针对双基机载雷达杂波分布特性方面的研究工作发表了大量的学术成果。Klemm和Zhang 等从单基雷达杂波模型出发,分析了几种特殊双基几何模型下的杂波特性,在此基础上阐述了单基杂波和双基杂波之间的物理关系。王永良等建立了收发平台前后同向飞行且无高度差场景下的双基几何模型,通过将发射机引起的杂波映射到接收机的方法构建了双基杂波空时分布的数学模型,并讨论了双基构型参数对杂波分布的影响。文献[6-8]中考虑了适应于任意双基场景下的几何模型,以接收机在水平面的投影点作为坐标系原点,收发平台基线或者接收机速度在水平面的投影作为轴/轴,建立本地几何坐标系,并刻画出了双基杂波回波模型。王慧娟等构建了一种地面固定坐标系来解决雷达配置场景处于时变状态的问题,并利用坐标变换法,推导得到了双基杂波数学模型。
现有文献中双基杂波多普勒频率均为关于收发平台与杂波点距离和以及接收机方位角的表达式,但实际情况中该方位角的取值范围并不清楚,无法直接通过遍历方位角的方法描述双基杂波分布曲线。本文充分考虑以往双基杂波模型存在的问题,提出了一种基于双基距离和以及等距离杂波环中心与杂波点连线相对于轴方位角的建模方法,根据几何关系推导出了杂波多普勒频率的计算公式。最后,通过数值仿真对比了3种典型双基构型下杂波的空时分布特性,分析了杂波分布随着双基几何构型参数变化的趋势。
1 双基地雷达几何场景建模
1.1 数学模型构建
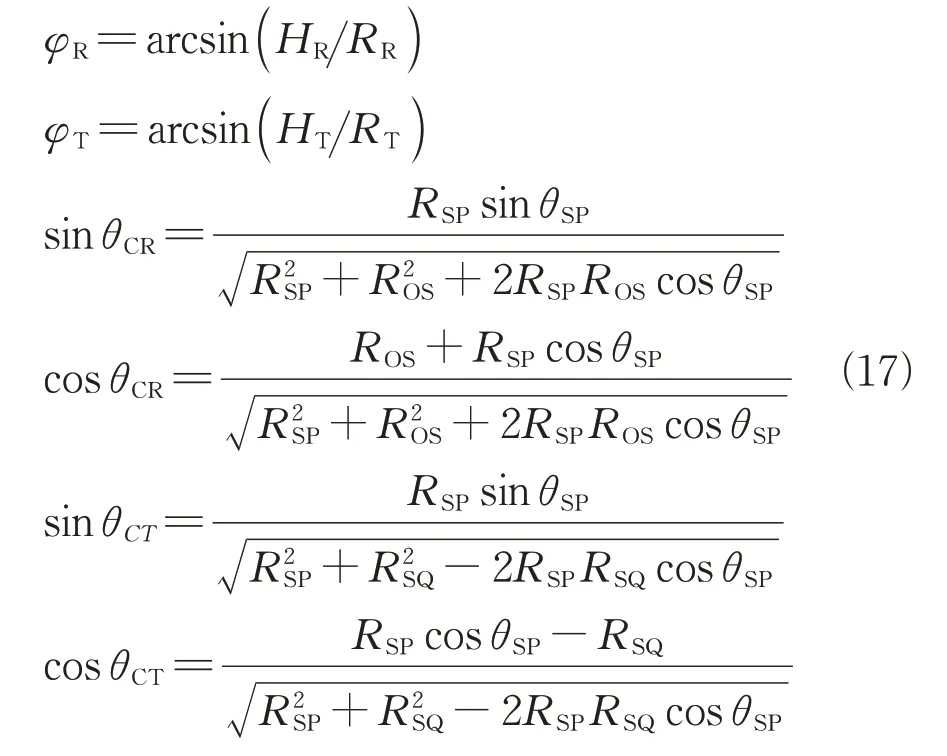
图1中展示了一般场景下的双基地机载雷达的几何关系。构建右手坐标系-:以接收阵面中心的地面投影点作为坐标原点,垂直地面方向向上为轴,接收和发射阵面中心之间连线在地面的投影为轴,在地面上垂直于平面的方向记为轴。发射和接收阵面的高度分别为和,两者之间的基线长度为,且基线和轴的夹角记为。发射阵面在地面投影点记为,发射和接收阵面中心分别记为和,和分别表示发射和接收阵面的载机速度。散射点相对发射与接收阵面的速度锥角分别为和,且散射点和发射接收阵面的斜距分别为和。与分别是散射点相对发射和接收平台天线轴向(在阵面后方往前看,左侧轴向)的锥角,与分别是发射和接收平台天线轴向与轴方向的夹角,和分别是发射和接收斜距相对于轴方向的方位角,和分别是发射和接收平台轴向与各自载机飞行方向的夹角,和分别是杂波散射体相对于发射和接收平台的俯仰角。点为地面双基等距离和曲线的中心,与杂波散射点构成的连线与轴的方位角记为(上述定义的角度均以逆时针方向为正)。

图1 双基地机载雷达几何构型关系图Fig.1 Geometry diagram ofbistatic airborne radar
1.2 等距离环解析表达式
杂波等距离环是由地面杂波散射点组成的一条轨迹环,该环可以划分为若干小的杂波单元,且每个杂波单元与发射和接收平台距离之和相等。由立体几何知识可知,双基距离和为的散射点分布在同一个椭球面上,该椭球面以发射和接收阵面中心和为焦点,长轴长为,对应的椭球面标准方程表示为

式中:

令:
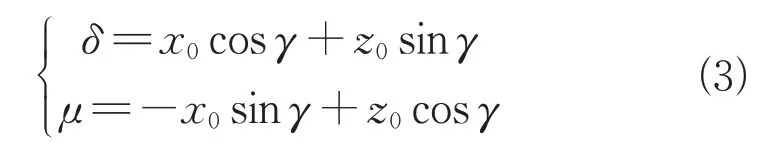
可将式(1)中椭球面方程重新描述为
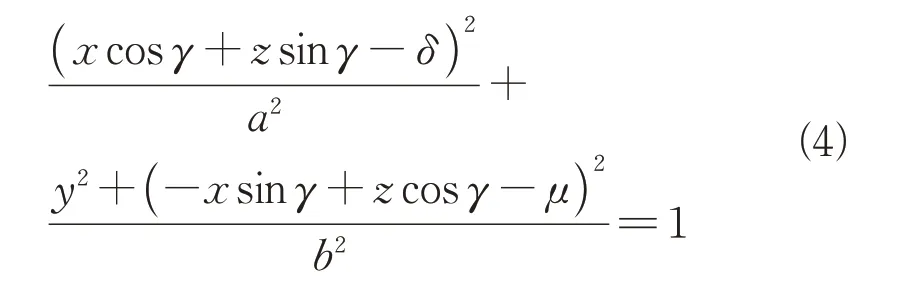
当收发平台基线长度低于一定量级时,可忽略地球曲率对杂波建模的影响。不失一般性,本文模型中考虑收发平台地面投影在同一平面内。此时,等距离环曲线是椭球面与地面水平面的交线,可通过式(5)计算其表达式。
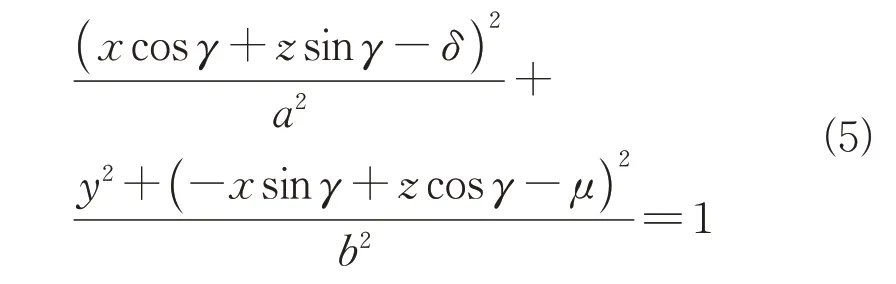
求解式(5)中的方程,可得杂波等距离环轨迹曲线的解析式为

式中:



将式(2)、式(3)和式(7)中的表达式代入式(8),化简可知收发斜距距离和需满足:
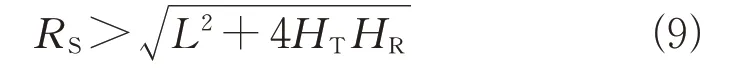
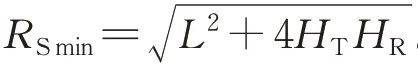
2 双基地机载雷达杂波建模
假设c(,)表示第个接收通道的第个脉冲接收到的第个距离环的杂波数据,则有

式中:为等距离环曲线方位向划分的个数;表示第个杂波点回波幅度,其幅度与接收阵面的子阵方向图、发射阵面的方向图、收发斜距距离和以及杂波散射系数(本文采用Morchin模型)有关;和分别为空域角频率和时域角频率,且任意杂波点对应的空时角频率可表达为

式中:表示阵元间的间距;是脉冲重复频率;为杂波单元的多普勒频率。杂波点与接收阵面轴线锥角的余弦值为

与单基雷达不同,双基雷达多普勒频率与收发平台的载机速度和速度锥角都相关,可表达为

杂波点与发射和接收平台速度的锥角余弦值为
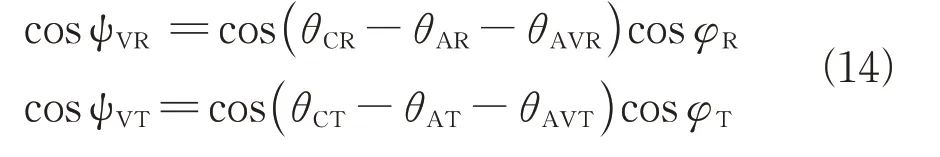
式(14)中cosψ和cos可以用包含cosψ和的表达式来描述。具体来说,以接收阵面中心作为顶点,接收阵面轴线作为旋转轴,ψ为顶角的一半,可构造一个空间圆锥体,联立圆锥体的方程和双基距离和为的等距离环方程能够求解出交点坐标。然后根据收发平台的空间坐标和几何关系,进一步可计算出cosψ和cos关于cosψ和的表达式。这种杂波空时分布的建模思路与单基杂波建模过程类似,但不太适用于描述双基杂波模型,其原因是单基杂波等距离环上的全部杂波点相对于接收机阵面中心的俯仰角均相同,当给定杂波点与接收机的距离时,可确定接收俯仰角。进而通过遍历360°方位的杂波点,就可以刻画出杂波多普勒频率与接收机空间锥角余弦值的分布曲线。而对于双基构型的杂波来说,等距离环上的杂波点相对于接收机的俯仰角是变化的,并且杂波与接收机阵面方位角的范围不再是-180°至180°(比如:等距离环曲线位于和之间),故无法确定杂波点与接收阵面轴线空间锥角的取值范围。
考虑到等距离环曲线中心点与杂波散射点的连线和轴的方位角的范围为-180°至180°,本文以变量和双基距离和构建杂波数学模型。根据几何关系和余弦定理可知:
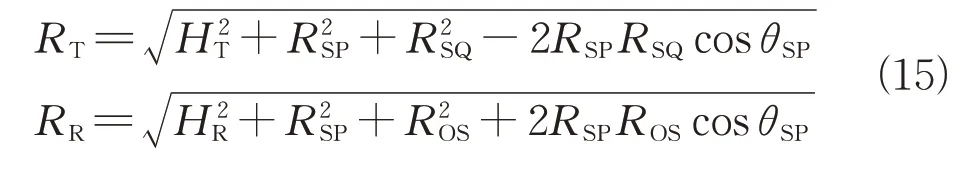
由于+=,可得到关于的一元二次方程为
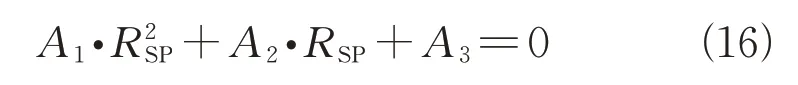
式中:

求解式(16)可得到(取正值)。杂波点方位和俯仰角的表达式分别为
总的来说,给定方位角和双基杂波距离和时:首先,求解式(16)得到等距离环中心与杂波点的距离;然后,根据式(15)计算收发平台与杂波点的斜距和;进而,根据式(17)得到杂波点与收发平台间的方位和俯仰角,并将式(17)和式(14)的结果代入式(13)和式(12)中,可得到杂波多普勒频率以及接收阵面轴线锥角的余弦值;最后,遍历全部方位角可获得同一个距离环上所有杂波点的空时分布曲线。
3 杂波分布仿真与结果分析
双基杂波分布受发射和接收平台的速度、高度、飞行方向与阵面轴线的夹角等因素的影响,且双基雷达系统中对应的飞行模式也千变万化。为了便于分析,本章主要针对3 种典型双基构型场景下的杂波分布进行了计算机仿真,对比了杂波分布特性随着双基距离和以及双基基线长度变化的趋势,并探讨了不同双基构型下的距离非平稳性对杂波抑制性能的影响,具体的系统仿真参数如表1所示。
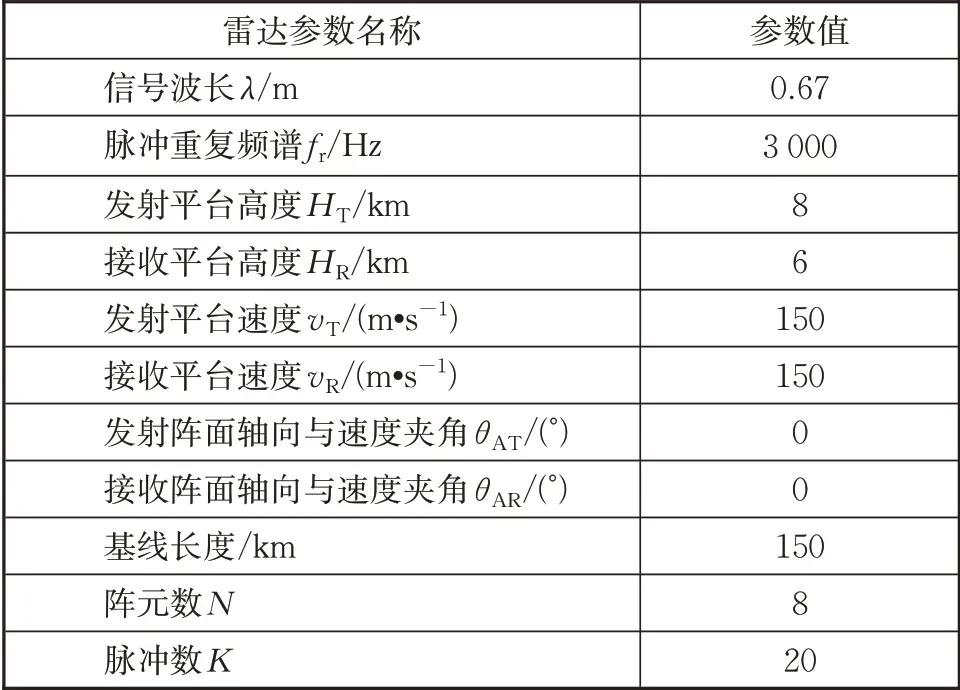
表1 双基雷达仿真参数Tab.1 Simulation parameters ofbistatic radar
3.1 不同几何构型时杂波分布特性
图2~4中展示了3种典型场景下,基线固定时不同双基距离和情况下的杂波空时分布曲线(基线长度=150 km),不同场景中图(a)表示整个距离环内全部杂波的分布情况,图(b)表示区分接收阵面前瓣和背瓣的结果。整体来看,杂波的空时分布呈现以下特点。
1)不同几何构型对杂波的空时分布影响较大,且均呈现出非线性的特点。
2)杂波分布在距离维表现出非平稳的特性,随着双基距离和的增加,非平稳程度变弱。
3)当杂波点位于收发平台基线在地面投影的连线上时,杂波分布基本不随双基距离和的改变而变化,杂波的距离平稳性较好。
图2描述的是发射和接收阵面载机飞行方向与两机之间基线在地面投影方向一致的场景。由于接收和发射阵面两侧的杂波都是完全对称的,所以背瓣和前瓣杂波分布完全一致。

图2 前后跟飞时杂波空时分布情况Fig.2 Space-time distribution of clutter for aligned flight
图3 描述的是发射机与接收机均平行飞行,且飞行方向垂直于基线方向的场景。当杂波点位于基线地面投影连线上时,与收发平台速度的方位角均为90°,故多普勒频率为0,且与双基距离和无关。由于同一距离环上的杂波点关于接收机的航线是非对称的,所以接收机阵面前瓣和背瓣接收的杂波分布不一致。另外,除了多普勒频率为0的杂波点外,随着双基距离和的减小,杂波距离非平稳性越明显。
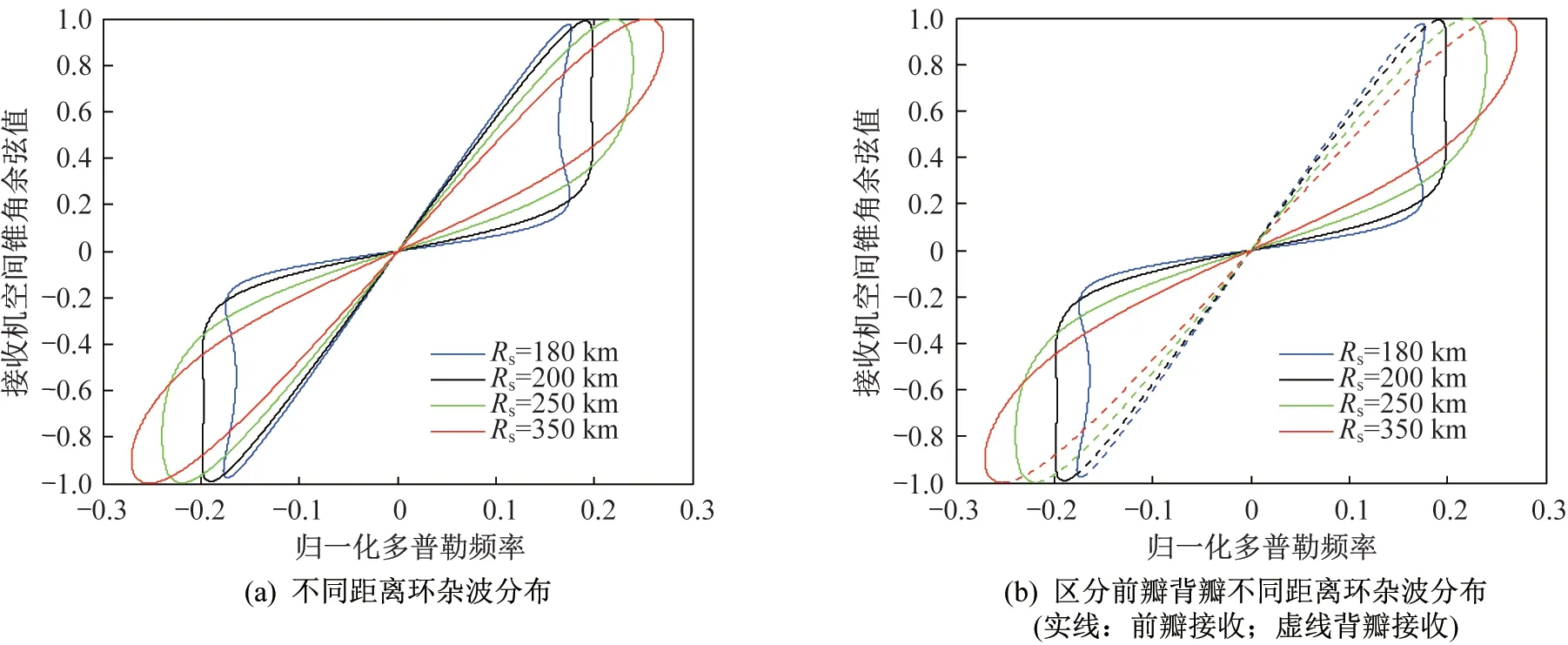
图3 平行飞行场景下杂波空时分布情况Fig.3 Space-time distribution of clutter for parallel flight
图4描述的是两架飞机交叉飞行的场景,其中:接收阵面轴线与轴方向的夹角=45°;发射阵面轴线与轴方向的夹角=-30°。由于杂波等距环曲线关于接收机航线非对称,且接收机前瓣接收到的杂波点多于背瓣接收到的杂波点,所以杂波空时分布曲线中前瓣的范围大于背瓣的范围。考虑到杂波分布距离维的非平稳性,随着双基距离和增大,杂波的距离相关性逐渐减弱。
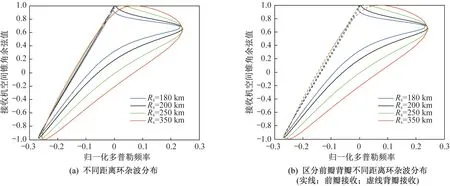
图4 交叉飞行时杂波空时分布情况Fig.4 Space-time distribution of clutter for intersecting flight
3.2 基线长度对杂波分布的影响
图5~7 给出了同一几何构型场景下基线长度对杂波分布的影响。改变收发平台的基线长度时,杂波的空时分布曲线变化明显,主要呈现以下规律:
1)随着基线长度的减小,杂波分布的距离非平稳性减弱。
2)当基线长度趋于0 时,双基几何关系变成单基形式。由于收发平台均为正侧视阵,所以典型场景1和2 中不同距离环下杂波空时分布趋向于一条直线,图5(a)、图6(a)中的仿真结果验证了该结论。
3)对于交叉飞行场景来说,当基线长度接近0时,杂波空时分布可近似为一个斜椭圆曲线形状,与图7(a)中的仿真结果相吻合。
图5描述的是两种基线长度时前后跟飞场景下的杂波空时分布情况,当基线长度从50 km 增加到100 km 时,不同双机距离和对应的杂波分布特性变得更加稀疏,进一步增强了距离维的非平稳性。

图5 前后跟飞不同基线长度杂波空时分布情况Fig.5 Space-time distribution of clutter with different baseline lengths for aligned flight
图6 对比了基线长度分别为50 km 和100 km 时,平行飞行双基场景下的杂波分布曲线。与前后跟飞的特性类似,降低基线长度会导致杂波距离相关性变弱。并且,当双基飞行构型演变为单基场景时,杂波空时分布将趋于一条直线,与传统的正侧视阵的杂波分布特性一致。
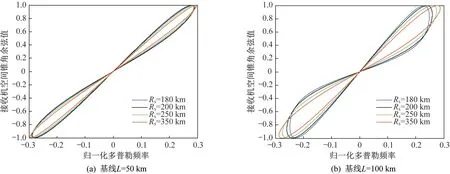
图6 平行飞行不同基线长度杂波空时分布情况Fig.6 Space-time distribution of clutter with different baseline lengths for parallel flight
图7描述的是不同基线长度时交叉飞行场景下的杂波空时分布曲线。可以看出,当基线长度由100 km减少到50 km 时,不同双基距离和的杂波距离依赖性减弱。另外,当基线长度进一步降低时,杂波空时分布曲线近似为斜椭圆形状。
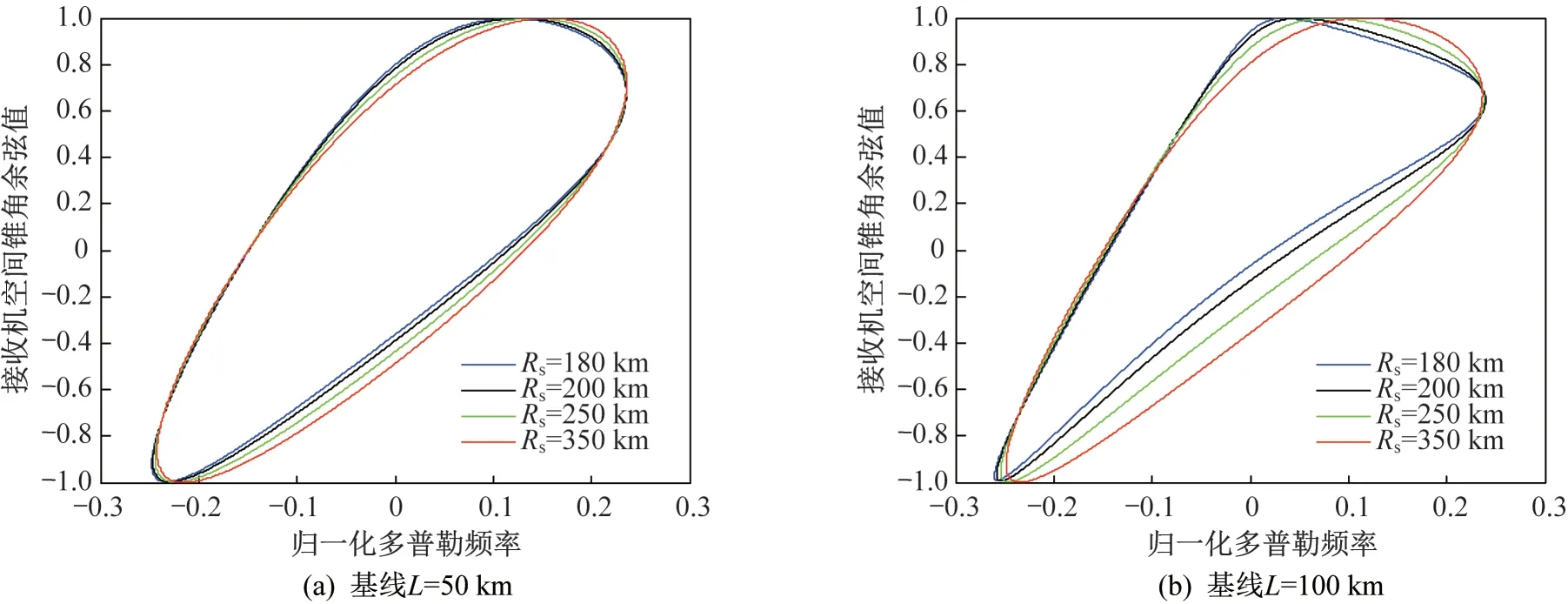
图7 交叉飞行不同基线长度杂波空时分布情况Fig.7 Space-time distribution of clutter with different baseline lengths for intersecting flight
4 结束语
本文以双基地机载雷达系统为研究对象,构建了适应于一般双基构型的几何模型,推导了双基杂波等距离环的解析表达式。在此基础上,提出了一种基于双基距离和以及等距离杂波环中心与杂波点方位角的建模方法,并根据对应的几何关系得到了杂波多普勒频率的计算式。仿真分析了3种典型场景下的杂波空时分布特性,结果表明双基杂波空时分布呈现出非线性和距离非平稳特性,并且增加杂波的双基距离和以及减小双基基线长度,会改善杂波的距离依赖性。
