基于卡方检验与SVM的多雷达抗欺骗干扰方法
2022-05-24施裕升王晓科周宇泰蒋国韬徐天洋
施裕升,王晓科,周宇泰,蒋国韬,徐天洋
(上海机电工程研究所,上海 201109)
0 引言
随着现代电子战争日趋激烈,有源欺骗式干扰因具有低成本、高性价比的特点而被广泛应用。尤其是数字射频存储器(digital radio frequency memory,DRFM)等先进器件的成熟为欺骗式假目标干扰的工程应用提供了有力支撑。DRFM 可以截获、存储、转发敌方雷达信号,在真实目标附近产生与其时域、频域和空域特征都十分相似的假目标,严重影响雷达对真实目标的跟踪精度,同时消耗雷达系统资源。
针对欺骗式干扰,单雷达的对抗方法研究发展迅速、效果显著。但是,单雷达视角单一,得到的环境信息有限,所能达到的抗干扰效能是有限的,对于高逼真度的有源假目标等复杂电子干扰场景,很难达到理想的对抗效果。因此,需要对雷达进行组网,利用多雷达之间的信息互补,提高雷达抗干扰能力和生存能力,适应未来战场环境需求。
目前,针对多雷达组网对抗距离欺骗假目标干扰,国内外已有大量研究成果,主要是基于真目标空间相关、假目标空间不相关的特点,采用卡方检验剔除假目标:文献[6]将角度量测卡方检验与距离量测均值和方差联合检验相结合,鉴别假目标;文献[7]将三坐标雷达的量测值转换至两坐标雷达所在的坐标系,构造卡方检验鉴别假目标;文献[8]将主动雷达的量测值转换至被动雷达所在的坐标系,通过点迹与航迹构造卡方检验鉴别假目标。但是,以上研究有两大问题:一是组网结构,异构组网相比同构组网对算法的适用性要求高,并且需要不断调整;二是探测角度差异,在较远区域,各雷达相对目标的角度差异较小时,假目标分散程度会下降,导致对假目标鉴别能力较差。针对问题二,文献[9]在位置信息的基础上引入速度信息进行假目标鉴别,但是,没有考虑到不同角度差异的鉴别算法选择,导致串行的算法比较复杂,并且为了保证算法的鉴别效果,至少需要3部测速雷达提供目标的速度信息作为支撑,实现条件较为苛刻。
基于以上分析,本文在同构雷达分布式组网的架构下,提出一种基于卡方检验与支持向量机(support vector machine,SVM)的自适应抗距离欺骗干扰的方法。该方法对假目标形成的航迹进行自适应鉴别:计算各雷达航迹间的马氏距离(卡方检验量),若只有一个组合满足卡方检验,说明假目标分散程度大,则采用卡方检验算法;反之,则挖掘航迹的多项特征,计算各雷达航迹间的欧式距离、兰氏距离,结合马氏距离作为SVM 的特征输入,最终将训练好的SVM 用于鉴别真假航迹。
1 问题描述
距离欺骗干扰指的是干扰机截获、存储雷达发射信号后,在雷达与目标的连线上产生具有一定欺骗距离的欺骗式假目标,在统一坐标系下假目标之间的空间位置是相对“分散”的。为论述方便,以2 部雷达探测为例,如图1所示。
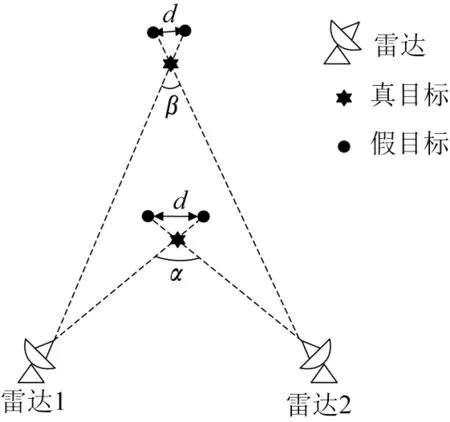
图1 不同角度差异下的真假目标示意图Fig.1 Schematic diagram of true and false targets under different angles
当2 部雷达的探测目标的夹角为时,假目标之间的空间分布位置较大,分散度较高。此时,采用卡方检验可知只有真目标之间的马氏距离(检验量)小于卡方检验门限,可有效剔除假目标。
但是,当2 部雷达的探测目标的夹角为时,目标与2 部雷达之间的距离较远,相对各雷达站的角度差异较小,假目标之间的空间分散程度明显下降,导致采用卡方检验算法时假目标之间的马氏距离也符合卡方检验要求,难以区分真假目标。此时,提高假目标鉴别能力最直接的办法就是增大各雷达间的布站间距。但是,雷达布站间距必需保证进行数据融合时雷达的威力范围有重合区域,而且布站间距过大也会导致数据通信延时等问题,为了满足角度差异较小情况下的鉴别能力需求,不断增大各雷达间的布站间距是不现实的。因此,需要从鉴别算法层面入手进行改进,以解决雷达探测目标夹角较小情况下的真假目标鉴别问题。
2 航迹的多特征挖掘
针对上述问题,基于单特征马氏距离的门限判别已无法有效地剔除假目标。因此,需要挖掘更多航迹特征,摒弃简单的门限判别方法,提出基于多特征训练的SVM分类器,可有效鉴别假目标。
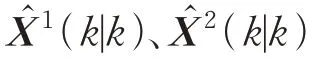
2.1 马氏距离(卡方检验)
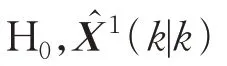
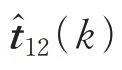
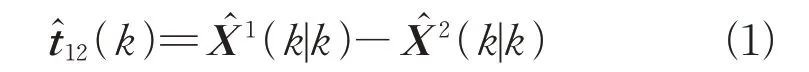
雷达1 与雷达2 的状态估计误差分别为(|)、(|),且相互独立,定义检验量(),即马氏距离计算式为
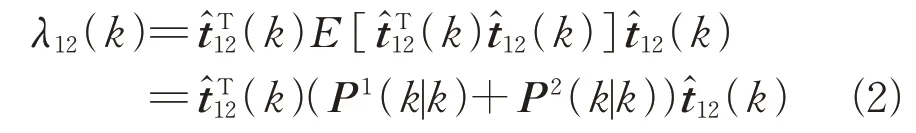
其检验量是服从自由度为的卡方分布随机变量,这里的为状态向量的维数。
将当前时刻与以前时刻的检验量进行统计,令
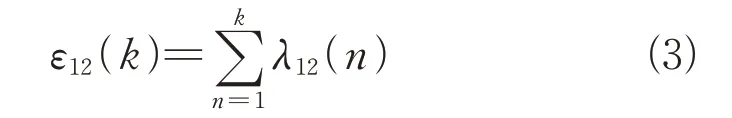
由于()服从自由度为的卡方分布,因此,如果()小于使用卡方分布获得的某一门限,则接受假设H;否则,接受假设H。
2.2 欧式距离
欧式距离也称欧几里得距离,是最常见的距离度量,广泛应用于衡量多维空间中两个点之间的绝对距离。将当前时刻与以前时刻的欧式距离量进行统计,构建航迹间的欧式距离特征,计算式为
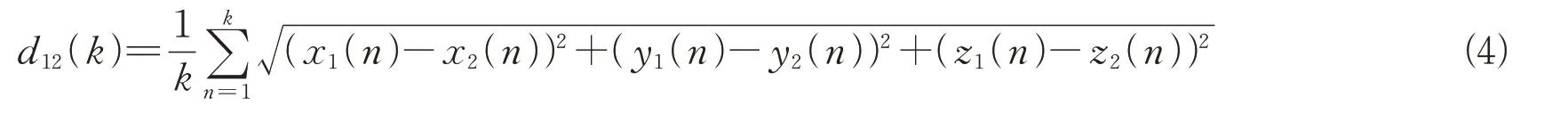
式中:()为第时刻的欧式距离统计量;[(),(),()]为第时刻雷达1的轴、轴、轴位置估计值;[(),(),()]为第时刻雷达2 的轴、轴、轴位置估计值。
2.3 兰氏距离
兰氏距离最早是由Lance 和Williams 提出的,是聚类分析中用于确定样本距离的一种常见方法。将当前时刻与以前时刻的兰氏距离量进行统计,构建航迹间的兰氏距离特征,计算式为
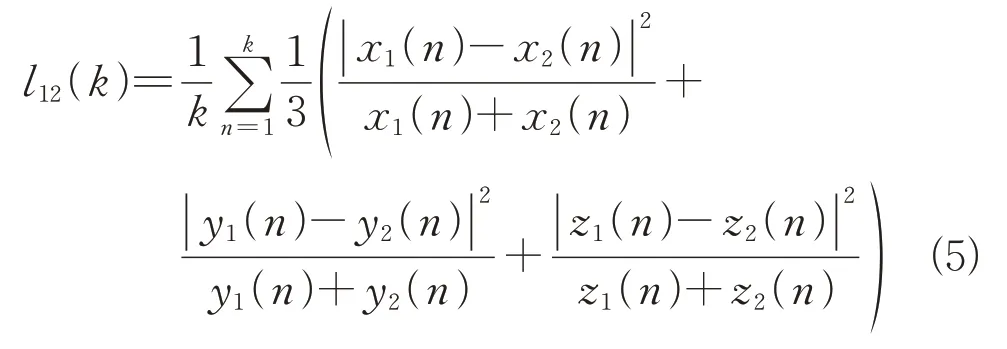
式中:()为第时刻的兰氏距离统计量;[(),(),()]为第时刻雷达1的轴、轴、轴位置估计值;[(),(),()]为第时刻雷达2 的轴、轴、轴位置估计值。
3 基于卡方检验与SVM 的自适应对抗方法
3.1 SVM分类原理
SVM是一种基于统计学理论的新型学习机,具有很好的学习能力和泛化能力。SVM 算法是由线性可分的二分类问题发展而来,基本思想就是在一个特征空间以最大间隔距离将两类样本分开,如图2所示。SVM 算法的目标就是寻找最优的模型参数和,构成最佳的超平面,使得该超平面与两类样本之间的间隔最大,即图中+=0所代表的超平面。
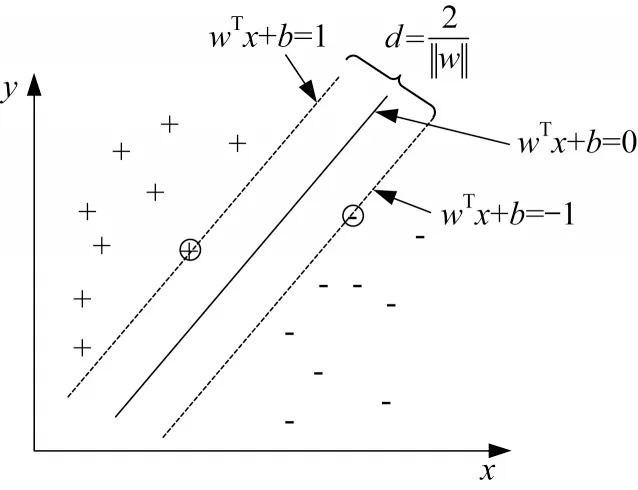
图2 SVM分类示意图Fig.2 SVM classification diagram
SVM 主要分为:线性SVM,通过间隔最大化处理严格线性可分的数据集;非线性SVM,通过引入核函数处理非线性数据集。由于真假航迹的鉴别就是一个二分类问题,因此,可将SVM 算法用于鉴别真假航迹。另外,在本文的问题中,假航迹之间的特征与真航迹之间的特征十分相似,分类问题具有非线性,因此,本文使用非线性SVM。
非线性SVM 针对非线性问题,使用核函数将训练样本从原始空间映射到一个更高维度的空间,使得样本在这个空间中线性可分,从而将非线性问题转换为线性可分问题。
假设训练集={(,),(,),…,}(x,y),x为特征向量,y为属性标签。令()表示将映射后的特征向量,即核函数。在特征空间内划分超平面所对应的模型可表示为
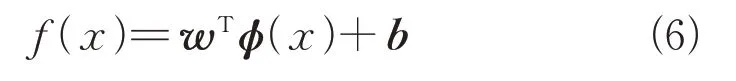
式中:()是划分2 个样本的超平面;和为模型参数,由式(7)所示的软间隔最大化方法求得。
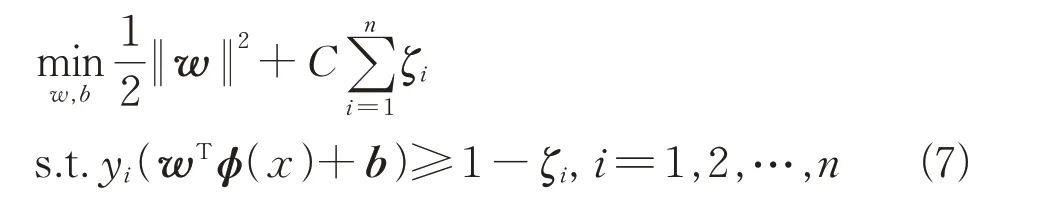
式中:ζ为松弛变量,表示允许存在一些误分类的点;为惩罚因子,表示对误分类的容忍程度。通过拉格朗日乘子法和对偶问题求解,可以求得最优的模型参数和,以及分类函数()。
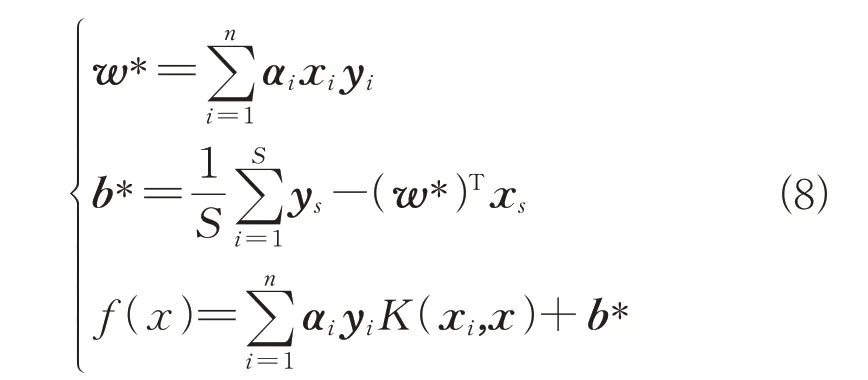
式中:α为拉格朗日乘子;为支持向量的个数;(x,y)为第个支持向量;(x,)为核函数,本文选用高斯径向基核函数。
3.2 自适应抗距离欺骗干扰的流程
为了提高组网雷达对抗距离假目标的能力,同时考虑到工程实用性,本文将传统卡方检验方法与智能SVM分类器相结合:在探测距离较近的场景下只有真目标之间的马氏距离满足检验条件,采用传统卡方检验即可识别假目标;在探测距离较远的场景下假目标之间的马氏距离也满足检验条件,需要更多的距离特征以进行分析,采用SVM 分类器识别假目标,既能提高各种距离下的假目标鉴别能力,同时也能提高实时性,保证工程实用性。以2 部雷达跟踪同一个目标为例,具体实现流程如图3所示。
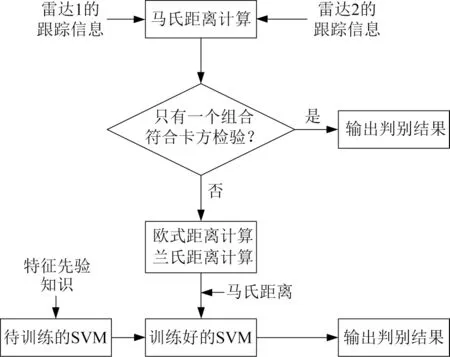
图3 自适应抗距离欺骗干扰的流程图Fig.3 Flow chart of adaptive anti-range deception jamming
主要步骤如下:
1)计算2 部雷达跟踪信息的马氏距离,包括真目标与真目标、真目标与假目标、假目标与假目标之间3种组合的马氏距离;
2)若只有1 种组合满足卡方检验的要求,则说明各雷达相对目标的角度差异较大,卡方检验足以解决该问题,直接输出判别结果,节省计算量;
3)若有1 种以上组合满足卡方检验的要求,则计算欧式距离和兰氏距离,并结合马氏距离作为SVM算法的特征输入;
4)将训练好的SVM 用于比较真航迹与假航迹间的特征差异,输出判别结果。
综上,通过判断卡方检验方法是否可用,能够自适应选择传统算法或智能算法,既保证了真航迹的识别率,又能保证整个算法的实时性。
4 仿真分析
仿真时,设置2个场景,进行3次实验:实验1模拟目标距离雷达较近的场景,卡方检验依旧适用,分析采用卡方检验的识别准确率;实验2 模拟目标距离雷达较远的场景,卡方检验无法适用,分析采用SVM 的识别准确率;实验3 是将上述2 个场景结合在一起,对比分析卡方检验、文献[9]算法、本文算法在整个过程的识别准确率。
4.1 实验场景1:目标距离雷达较近,采用卡方检验的识别准确率分析
仿真场景设置为:2 部三坐标雷达作为节点雷达的组网模型,在北天东坐标系下,融合中心的位置为(0,0,0),雷达1 的位置为(0,0,5 km),雷达2 的位置为(0,0,-5 km)。在位置为(5 km,6 km,5 km)处设置1 个真目标,目标运动速度为(200 m/s,-10 m/s,200 m/s)。该目标对每个雷达站施放2 个欺骗距离为200 m 的假目标,分别位于真目标前方和后方。假设欺骗目标已形成稳定航迹,2 部雷达的跟踪时间为200 s。
计算真航迹与真航迹之间、真航迹与假航迹之间、假航迹与假航迹之间的马氏距离,如图4所示。从图4 中可以看出,只有真航迹之间的马氏距离明显较小,对每个时刻的马氏距离求和后得到总体马氏距离为981,小于卡方检验门限(显著水平为0.05),因此,通过门限判别可有效鉴别真假航迹,真航迹的识别率为100%。
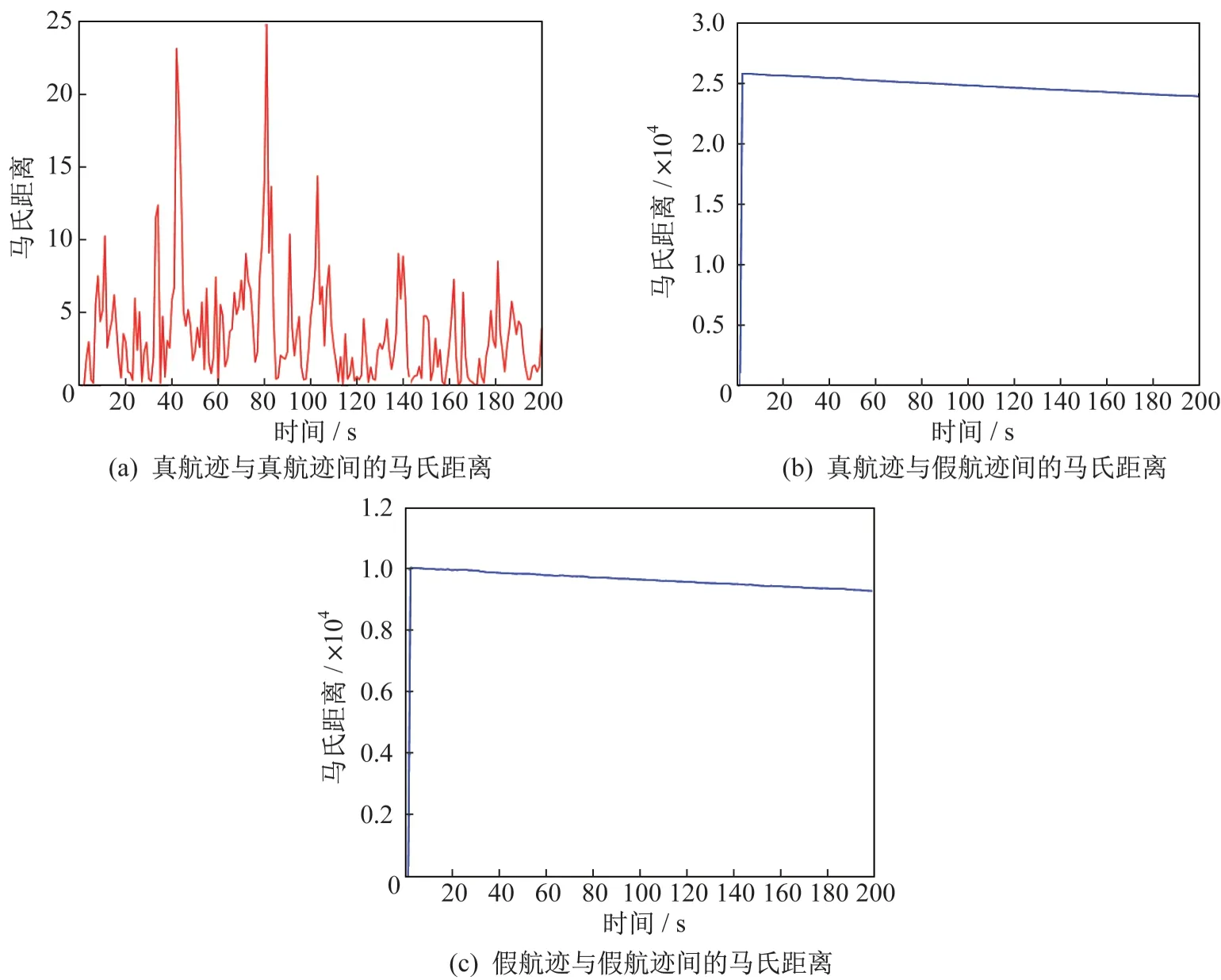
图4 各雷达航迹之间的马氏距离Fig.4 Mahalanobis distance between radar tracks
4.2 实验场景2:目标距离雷达较远,采用SVM的识别准确率分析
仿真场景设置为:2 部三坐标雷达作为节点雷达的组网模型,在北天东坐标系下,融合中心的位置为(0,0,0),雷达1 的位置为(0,0,5 km),雷达2 的位置为(0,0,-5 km)。在位置为(100 km,6 km,100 km)处设置1个真目标,目标运动速度为(200 m/s,-10 m/s,200 m/s)。该目标对每部雷达站施放2 个欺骗距离为200 m 的假目标,分别位于真目标前方和后方。假设欺骗目标已形成稳定航迹,雷达1 跟踪真航迹前方和后方的欺骗假航迹编号分别为1.1 和1.2,雷达2 跟踪真航迹前方和后方的欺骗假航迹编号分别为2.1 和2.2。每部雷达的跟踪时间为200 s。
计算真航迹与真航迹、假航迹编号1.1 与假航迹编号2.1、假航迹编号1.2 与假航迹编号2.2 之间的马氏距离,如图5 所示。从图5 中可以看出,假航迹之间的马氏距离也符合卡方检验的门限,此时,采用马氏距离最小的组合为真航迹组合,但识别率较低,仅为37%。
在此场景下,虽然假航迹之间的马氏距离也符合卡方检验,但是从图5可以看出,真航迹之间与假航迹之间的马氏距离变化特征是不一样的。为了更全面地验证真航迹之间特征与假航迹之间特征的不同,计算欧式距离和兰氏距离,如图6 所示。从图6 中可以看出,假航迹之间的欧式距离和兰氏距离变化基本一致,以此可以区分真航迹与假航迹。
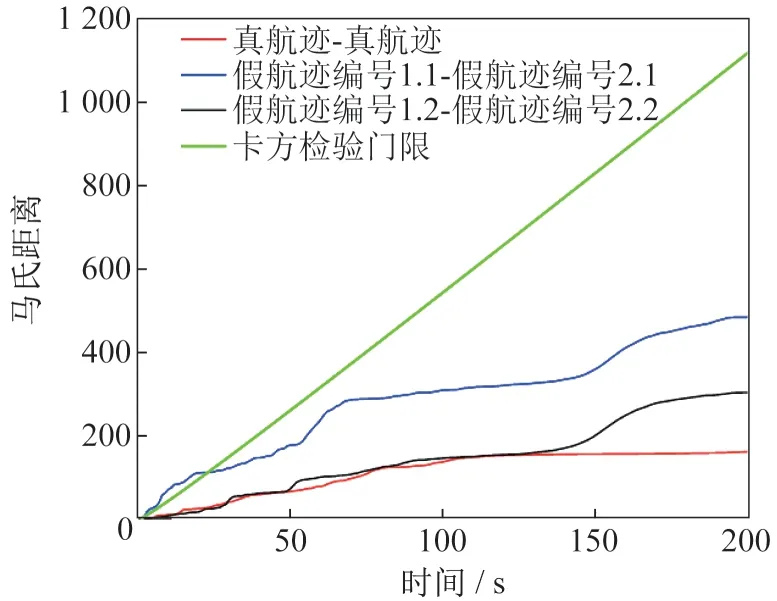
图5 卡方检验不适用时的马氏距离Fig.5 Mahalanobis distance when the chi-square test is not applicable
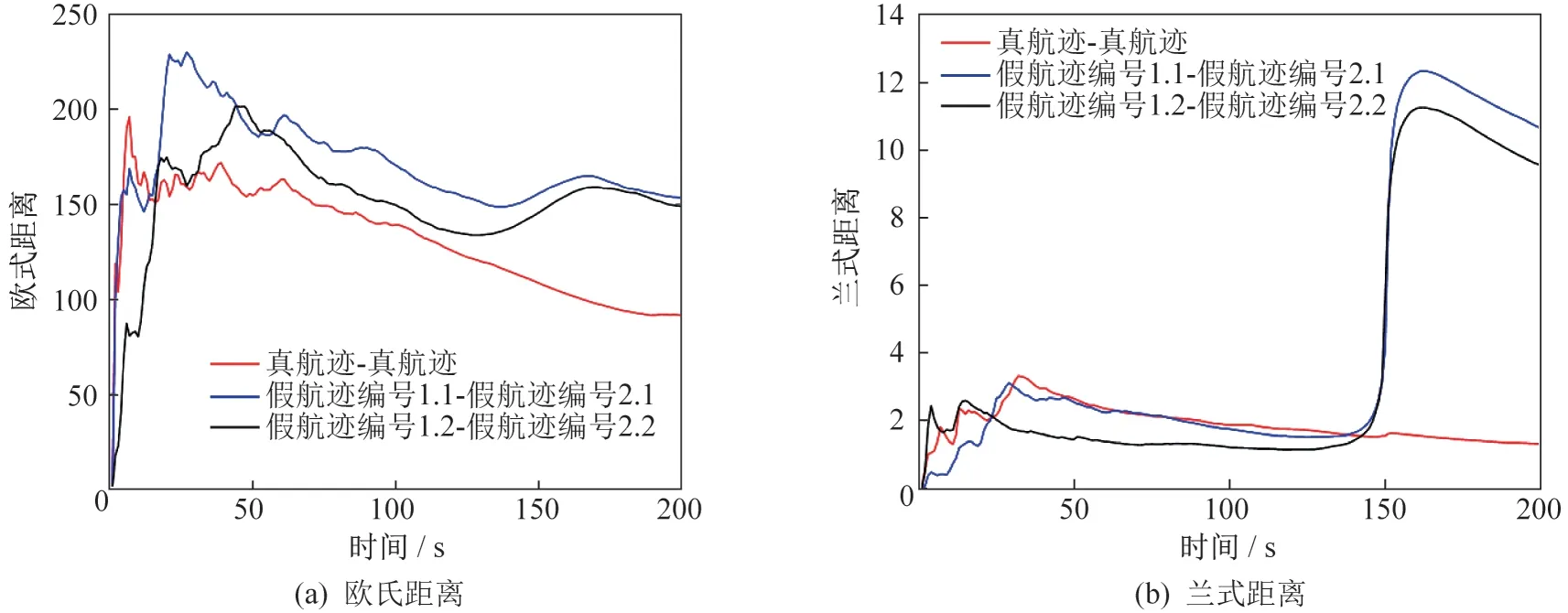
图6 不同航迹间的欧式距离与兰氏距离Fig.6 Euclidean distance and Randolph distance between different tracks
将不同航迹间的马氏距离、欧式距离、兰氏距离作为SVM 的特征输入,训练SVM,得到不同训练样本数量下的真航迹识别率,如图7 所示。从图7 中可以看出,训练样本个数为20 时,真航迹识别率基本保持在90%以上,准确度较高。此外,训练时间仅为5.9 ms,分类时间仅为0.7 ms,实时性较好。
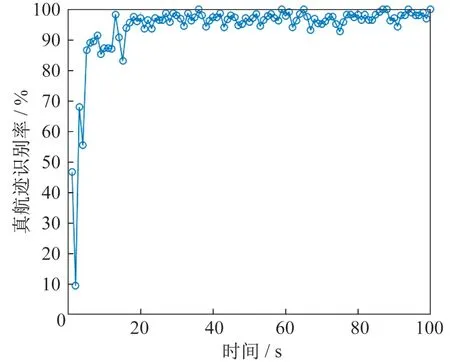
图7 训练样本数与真航迹识别率的关系图Fig.7 The relationship between the number of training samples and the true track recognition rate
为了验证采用3个特征的合理性,比较单特征、双特征、三特征、四特征(增加闵氏距离)作为SVM 的输入,将不同特征类型取得的真航迹识别率的平均值作为最终的真航迹识别率,结果如表1 所示。从表1 中可以看出,随着特征个数的不断增加,真航迹的识别率也在提高。但是,当SVM 输入的特征个数为4 时,真航迹识别率的提升不是很明显,因此,考虑到计算量与识别率,采用三特征作为SVM输入。

表1 SVM不同输入特征类型数的真航迹识别率Tab.1 True track recognition rate of SVM with different input characteristics
4.3 实验3:对比分析
为了验证本文算法的优越性,将上述2 个场景整合到一个场景内,对比分析不同距离下本文算法与文献[9]算法、卡方检验算法的真航迹识别率,结果如表2所示。从表2中可以看出,卡方检验明显不适用于远距离目标场景。为了解决该问题,文献[9]在卡方检验的基础上引入了速度信息,其真航迹识别率略优于卡方检验的真航迹识别率,但受限于只有2 部雷达的测速信息,文献[9]算法的真航迹识别率明显比本文算法的真航迹识别率差。另外,本文算法的线下训练时间较短,线上识别时间与卡方检验相当,工程应用性较强。
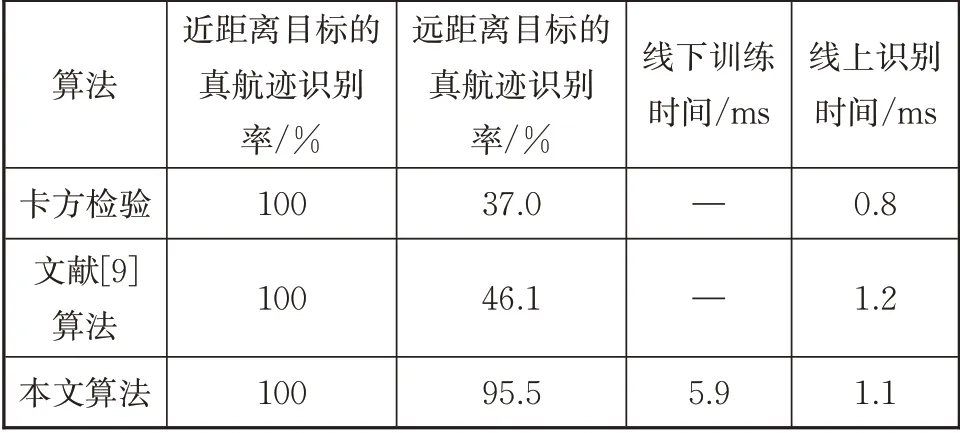
表2 不同算法的对比结果Tab.2 Comparison results of different algorithms
5 结束语
针对各雷达相对目标的角度差异较小时传统方法(卡方检验)鉴别假目标能力较差的问题,提出了一种基于卡方检验与SVM 的自适应抗距离欺骗干扰的方法,该方法能够根据传统方法的适用性自适应切换算法,在提高真目标航迹识别率的同时保证了实时性。仿真结果表明,本文方法在不同探测距离下识别真目标的能力都较好,其中远距离探测场景下真航迹识别率为95.5%,明显优于卡方检验(37.0%)以及改进卡方检验(46.1%)的真航迹识别率。此外,本文方法训练时间短,识别时间与传统方法相当,实时性好,工程应用性强。
