基于复单脉冲比和变尺度离散变换的拖曳式诱饵干扰识别技术研究
2022-05-24赵婵娟袁云权陈言理李姗姗
秦 琨,赵婵娟,袁云权,陈言理,李姗姗
(1.上海航天电子技术研究所,上海 201109;2.火箭军装备部驻上海地区军事代表室,上海 201109)
0 引言
现代防空中,防空导弹武器系统都是在电子干扰环境下实施对空作战。在这样的作战环境下,防空导弹武器系统的作战效能都会有某种程度的下降。因此防空导弹武器系统中的搜索雷达和跟踪制导雷达均应具备良好的抗干扰功能,尤其是抗主瓣干扰的能力。中程防空导弹武器系统在作战过程中,其面临的只保留人为电子战威胁主要来自两个方面:一是敌方电子战飞机所实施的支援式和掩护式干扰;二是敌方战机或导弹所实施的自卫式干扰。拖曳式干扰是一种自卫式平台外欺骗干扰,是作战飞机对付主动导引头或机载制导雷达自卫式平台外有效欺骗干扰的手段之一。拖曳式雷达诱饵(towed radar active decoy,TRAD)又称为牵引式雷达诱饵,是由被保护的目标载体通过拖曳线牵引并随着载体一起运动的雷达假目标,主要用于对机载平台进行保护。由于拖曳式诱饵是通过拖曳线在载机的牵引作用下随着载机的运动而运动,其运动速度和方向与载机的几乎相同,可以很好地模拟载机的航速与航向等运动特征,从而使一般的跟踪制导雷达难以通过运动特征来区分出载机与诱饵。在中远距离时,由于载机与诱饵同处于雷达半波束之内,使得雷达角度跟踪系统无法分辨;当雷达的距离分辨力较低时,目标和诱饵可能会分布在同一个径向距离分辨单元内,因此也无法利用距离信息实现目标和诱饵分离。在这种条件下,必须通过除距离维外的其他多目标参数区分目标和诱饵。本文从目标与诱饵的信号分布特性和多普勒频谱特性角度出发,利用复单脉冲比和变尺度离散Chirp-Fourier变换提出一种简单有效的拖曳式诱饵检测分辨技术,实现拖曳式诱饵和目标分离。
1 拖曳式诱饵干扰机理分析
拖曳式诱饵干扰是由目标载机通过光纤拖曳一个有源干扰发射装置转发雷达信号,对雷达实施假目标欺骗干扰,此时载机会通过机动形成载机、诱饵、导弹之间的三角态势。在中远距离上,由于载机与拖曳式诱饵之间作用距离短,运动特性近乎相同。因此,不管是迎头、尾追还是截击,载机回波与诱饵干扰信号的多普勒频率之差小于脉冲多普勒(pulse Doppler,PD)制导雷达的多普勒频率分辨单元宽度,二者的多普勒谱线几乎重合,很难进行分辨和识别。但当载机接近时,载机、诱饵与雷达间的张角逐步增大,雷达视场中出现2个目标(载机和诱饵),如果雷达没有多目标处理能力,则可能选择诱饵进行跟踪,从而被干扰。当张角大于制导雷达波束宽度的1/2 时,若雷达跟踪的是诱饵,载机将处于雷达波束以外,制导雷达将丢失真目标;此后,如果诱饵关机和回收,将导致制导雷达丢失跟踪信号,如果不关机,将导致导弹跟踪和命中无价值的诱饵。两种雷达探测视角下的拖曳式诱饵战场态势如图1 所示(图中表示雷达与载机和诱饵间的距离)。

图1 两种雷达探测视角下的拖曳式诱饵战场态势Fig.1 Situation of towed decoy under two radar detection angles
在三角态势下,随着载机不断接近机载火控雷达,载机目标回波与诱饵干扰信号的多普勒频率之差将逐步增大,有可能在某个距离上超过PD 制导雷达的多普勒频率分辨单元宽度,即载机目标回波的多普勒谱线与干扰信号多普勒谱线将逐步分离。因此,速度维的“不可分辨”是一个相对概念,它是相对于雷达的速度分辨率和测速精度而言的。虽然,目标在施放诱饵时,诱饵是被目标拖着飞行的,理论上诱饵的飞行速度和目标的飞行速度是一致的,导致雷达无法在速度维上区分目标和诱饵。但当释放诱饵或目标拖着诱饵在空中飞行,由于诱饵和载机逐渐接近雷达或受到大气气流以及飞机紊流的影响,诱饵与目标之间的相对速度会发生波动,存在一定的速度差。如果雷达的测速精度和速度分辨率足够高,就能从速度维上将目标和诱饵区分开。例如,对于C波段雷达来说,如果多普勒分辨率达到Hz级,那么雷达在速度维上的分辨率就可达到10m/s,这足以区分一般的目标和诱饵。最后,在能区分目标和诱饵速度维多普勒谱线的条件下,可根据诱饵干扰信号和目标信号功率的不同,一般干扰信号的功率比载机回波信号的功率要大,让雷达选择较弱的目标谱线进行检测跟踪。
2 雷达拖曳式诱饵速度多普勒频谱分析
2.1 单脉冲雷达拖曳式干扰存在可检测性分析
雷达对抗拖曳式诱饵首先要解决的问题就是对诱饵的存在与否进行检测,拖曳式诱饵存在性检测是抗干扰的前提和基础。基于拖曳式干扰对单脉冲雷达的干扰机理分析可知,判断是否存在拖曳式干扰,某种程度上可以看成是对雷达同一分辨单元内多目标的检测。针对这种波束内的多目标的检测问题,Blair 等、Nandakumaran 等、Sinha 等进行了卓有成效的研究,提出了一系列理论算法,主要包括推广正交法、复角检测法等。然而,传统单脉冲算法能够在单目标情况下被用来精确地估计仅取决于目标角位置的误差角,但是在雷达距离分辨单元内存在多个目标时,单脉冲比值就不是一个实数,而是一个复数,也称作复单脉冲比。传统单脉冲算法只关注单脉冲比值的实部,但是在判断距离分辨单元内是否存在多目标时,虚部具有指标意义。因此利用复单脉冲比虚部在有无拖曳式干扰两种情况下的差异性进行分析,可实现单脉冲雷达对拖曳式诱饵的检测。


式中:为目标回波信号的幅度;为诱饵回波信号的幅度;为信号载频;()为目标回波信号相位;()为诱饵回波信号相位。
经过单脉冲雷达和差通道输出的和信号与差信号分别为
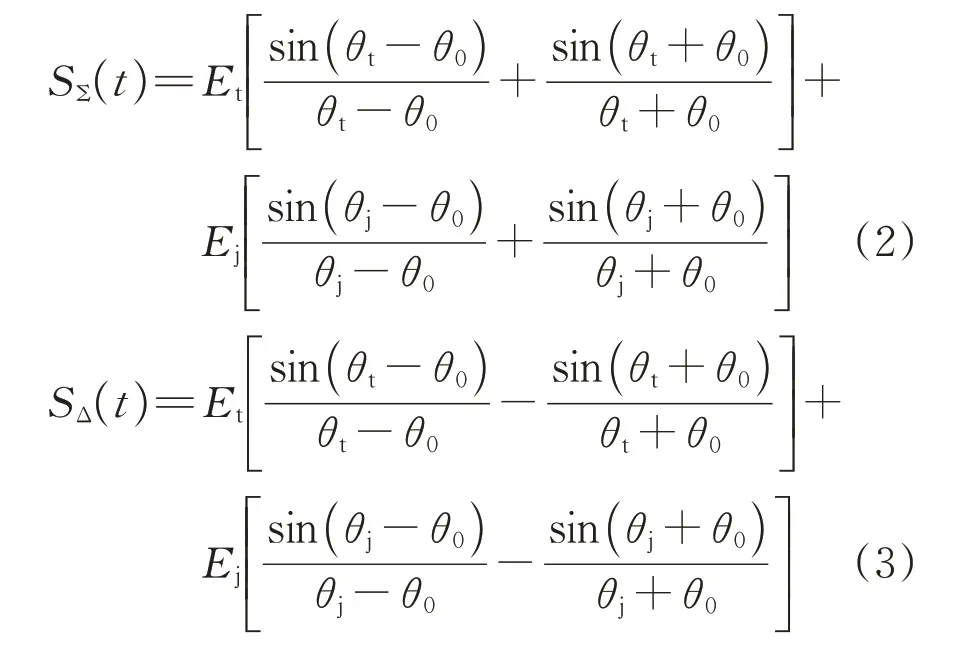
式中:为目标的方位角;为诱饵的方位角。
根据单脉冲测角时差和比的计算公式可得到复单脉冲比的虚部为

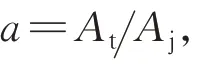
当雷达波束内只存在单个目标时,复单脉冲比的虚部为0,但在雷达实际工作情况下,由于通道特性的差异(噪声或接收通道幅相不一致性),和通道与差通道信号之间的相角差不一定等于0°或180°,因此式(4)的值也不一定为0,可能是一个接近于0 的比较小的数。当雷达波束内既存在目标又存在诱饵时,复单脉冲比的实部就由目标和诱饵的回波信号共同决定,用该实部获得的角度就不再是目标的真实角度,而此时复单脉冲比的虚部也不再为0。由式(4)可知,其虚部大小会随干扰信号的幅度、相位以及目标和诱饵与雷达之间的张角的大小变化进行波动。根据上述分析,由于单目标时复单脉冲比的虚部可能不为零,因此考虑通过设置一定的门限对复单脉冲比的虚部进行检测判断,就可以辨识目标载机是否施放了诱饵。单脉冲比值虚部大小随信号不同相位及诱饵与目标张角的变化关系如图2~3所示。

图2 不同相位差变化时复单脉冲比虚部曲线Fig.2 Imaginary part curve of complex monopulse

图3 诱饵与目标张角变化时复单脉冲比虚部曲线Fig.3 Imaginary part curve of complex monopulse
2.2 变尺度离散Chirp-Fourier变换
通过对干扰后的信号进行存在检测性分析后,确定同一主波束宽度内存在多个目标或干扰。因此,理论上只要提高雷达的多普勒分辨率就能对拖曳式诱饵这种双点源的多源干扰进行分辨。但传统的离散傅里叶变换(discrete Fourier transform,DFT)是在观测时间内从整体上描述信号的频谱,对局部频谱信息缺乏描述,无法极为精确地测量目标和诱饵的多普勒频率,而且在实际应用过程中,目标和诱饵相对于雷达的测量视角在不断地发生变化的同时会引起频谱展宽,从而降低目标的多普勒测量精度。因此采用变尺度离散Chirp-Fourier 变换对本文中的多目标进行分辨能够有效地解决上述问题。
当脉冲多普勒(pulse Doppler,PD)雷达和目标之间存在相对加速度时,回波脉冲为Chirp 信号,经过单边带滤波器之后,回波脉冲串变为连续波,称为一个较长的Chirp信号。
设雷达接收的匀加速目标的回波信号由连续Chirp信号表示为

式中:表示调频起始频率;表示调频斜率;表示信号幅度值。
由速度公式可推导出起始频率和调频斜率与目标相对初速度和加速度之间的关系为

代入式(6)可得

用采样间隔为的时钟对上述信号进行离散化,同时用旋转因子的形式对式(7)重新进行表达,可得

式中:表示初始相位;表示归一化速度因子;表示归一化加速度因子;W为转换的旋转因子;为离散点数。
和与和的关系为

因此有

可推导出相对速度和相对加速度与和的关系为

综合上述推导过程,定义离散信号(),长度为,它的变尺度离散Chirp-Fourier 变换及其逆变换可表达为


根据上述定义不难发现,对于任意固定的和值,其点的变尺度离散Chirp-Fourier 变换实际上就是信号()W
的离散傅立叶变换。
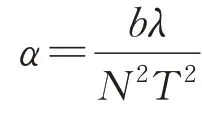
由于将速度和加速度联合分辨时碰到模糊的概率要小于单独分辨速度或加速度时的概率,另外当加速度匹配因子和尺度因子相匹配时,变尺度离散Chirp-Fourier 变换的加速度分辨率最高,提出一种单脉冲雷达PD 模式下可行的多目标分辨流程,如图4所示。

图4 基于变尺度离散Chirp-Fourier变换的多目标分辨流程Fig.4 Multi-target identification process based on variable scale discrete Chirp-Fourier transform
3 仿真分析
仿真条件设置如下:①X 波段PD 雷达系统——脉冲重复频率f=200 kHz,波长λ=0.033 m,积累时间为5 ms,信号采样点数为2 048,尺度因子=0.001,=60;②噪声为归一化高斯白噪声,时域干信比20 dB。仿真场景设置如下:设在雷达观测范围内,当载机投放诱饵过程中,目标载机速度为300 m/s,拖曳式诱饵速度为200 m/s,加速度分别为=80 m/s,= 60 m/s,雷达与目标、诱饵的相对位置关系如图5所示。

图5 雷达与目标、诱饵间的空间位置关系Fig.5 Spatial position relationship between radar,target and decoy
3.1 诱饵与目标间加速度判别
由拖曳式诱饵的运动特性可知,虽然载机和诱饵通过拖曳线相连,它们的运动速度大致相同,但是由于受到大气气流等因素的影响,或是在载机释放诱饵初期,载机和诱饵在某个时间段内相对于雷达的加速度不可能完全相同,且释放初期具有较大的加速度差异。通过对采集的脉冲串信号进行变尺度离散Chirp-Fourier 变换,由图6 可知,仿真结果有两个明显的峰值,说明检测到了两个目标。
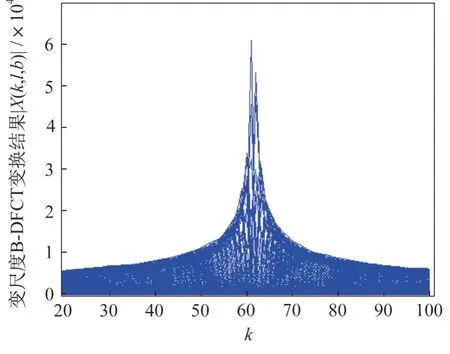
图6 加速度差异多目标鉴别Fig.6 Acceleration difference multi-target
由于和的表达式可表示为

式中:v为目标的初速度;为雷达发射信号的脉冲重复周期;为雷达发射信号的波长;为目标的加速度。由式(8)、式(12)和式(13)可推知

按仿真条件设定值,由式(14)可以得到其加速度分辨力Δ的值约为Δ=0.82 m/s。也就是说,对于两个点目标而言,如果它们的加速度之差超过了0.82 m/s,那么目标回波信号的变尺度离散Chirp-Fourier变换(Bdiscrete Chirp-Fourier transform,B-DCFT)谱将呈现出两个或多个谱峰,这样可以利用多普勒谱的加速度信息对拖曳式干扰的双点源目标进行分辨。
3.2 诱饵与目标间速度判别
当目标与诱饵平稳飞行时,目标与诱饵间加速度间差异将变小。这时,可通过速度间的差异进行判别。由于受到大气气流等因素的影响,目标载机与诱饵间必然存在速度差异。由PD 雷达体制的特性可知,脉冲多普勒雷达的速度分辨能力主要取决于信号的时宽,雷达的多普勒分辨率和速度分辨力之间存在着如下关系

根据仿真场景设定,PD 分辨力可达到Δ=200 Hz,可推算其速度分辨力可达到Δ=0.82 m/s,足以区分一般的目标和诱饵。如图7 所示,仿真结果有两个明显的峰值,说明检测出两个不同的速度值。

图7 速度差异多目标鉴别Fig.7 Speed difference multi-target
3.3 速度与角速度联合判别
图8 为变尺度离散Chirp-Fourier 变换的三维检测结果。在三维立体观测结果中,可以很明显的观测出两个峰值,通过联合判别,在速度维或加速度维上至少有一项差异大于最小分辨力,只要存在差异,就可以通过联合判别检测出差异峰值。

图8 变尺度离散Chirp-Fourier变换的三维检测Fig.8 Three-dimensional detection of variable scale discrete Chirp-Fourier transform
仿真结果表明,在拖曳式诱饵条件下,当雷达对于拖曳式干扰这种多目标的速度分辨率足够时,若雷达为迎头探测,载机的多普勒速度会小于诱饵的多普勒速度,从MTD的窄带滤波器组中选择相应的滤波器输出(即选通)后送入单脉冲测角系统进行角度测量,便能够削弱诱饵对单脉冲测角系统的影响;同理,在雷达尾追探测时,载机的多普勒速度会大于诱饵的多普勒速度,通过选通载机对应的谱线,导引头同样能够削弱诱饵的影响。
4 结束语
基于关于不可分辨目标检测的研究基础,结合拖曳式诱饵的干扰特点,通过数学推导和仿真分析,研究了拖曳式诱饵存在与否导致的复单脉冲比虚部的差异,实现了对诱饵的存在性检测。根据诱饵存在的检测结果,再利用变尺度离散Chirp-Fourier 变换进行时频分析处理,在某些特定条件下对拖曳式干扰具有极强的区分能力。仿真验证结果表明,整个算法处理流程简单有效,适用于工程应用。但是在工程应用时也存在一些缺点,比如积累时间长、算法运算量大、低信噪比条件下分辨效果急剧下降等,所以在实战条件下对以拖曳式诱饵为代表的多目标环境下的探测仍然存在很大的不确定性,需要继续展开研究。
