某型发动机测量耙结构损伤分析及优化设计*
2022-05-20贾文杰
贾文杰,孙 科
(中国飞行试验研究院,陕西 西安 710089)
0 引 言
在航空发动机飞行试验中,通常需要使用压力和温度受感器测量发动机流道内的各种压力和温度信号,通过当地的总压、静压、流动方向和温度等数据来确定发动机的各个性能参数,因此受感器的设计具有重要的意义。目前航空发动机流道参数测量主要通过测量耙来实现[1]。测量耙通过根部安装座固定在发动机机匣壁面上,耙体伸入流道中,受到沿轴向来流的气动载荷和发动机振动产生的振动载荷,而测量耙的结构强度直接影响试飞安全,因此其结构设计具有非常重要的意义。目前,陶冶等人[2-4]已经针对测量耙的模态特性、动态特性和应力分布特性展开了相应的研究;李秋峰等人[5-6]研究了不同结构的测量耙对发动机流场参数的影响;目前,国内外针对测量耙的研究已经较为成熟,并制定了相应的规范和标准[7-9]。
某型发动机进气道出口截面设计的总温总压复合测量耙,在振动试验过程中耙体支撑杆部位产生裂纹,证明其构可靠性较差,无法满足装机试飞要求,因此重点对其结构损伤原因进行分析,并对测量耙结构进行优化设计。通过数值仿真和环境试验的方法对优化后的测量耙进行分析,证明了改进后的测量耙满足某型发动机装机飞行试验的要求。
1 结构损伤分析
用于配装某型发动机进气道的复合结构测量耙如图1所示,其主要由安装座、测量耙主体和填充橡胶组成,安装座和测量耙主体部分采用1Cr18Ni9Ti不锈钢材料制成,填充材料为硫化橡胶,20 ℃下各材料属性如表1所列。
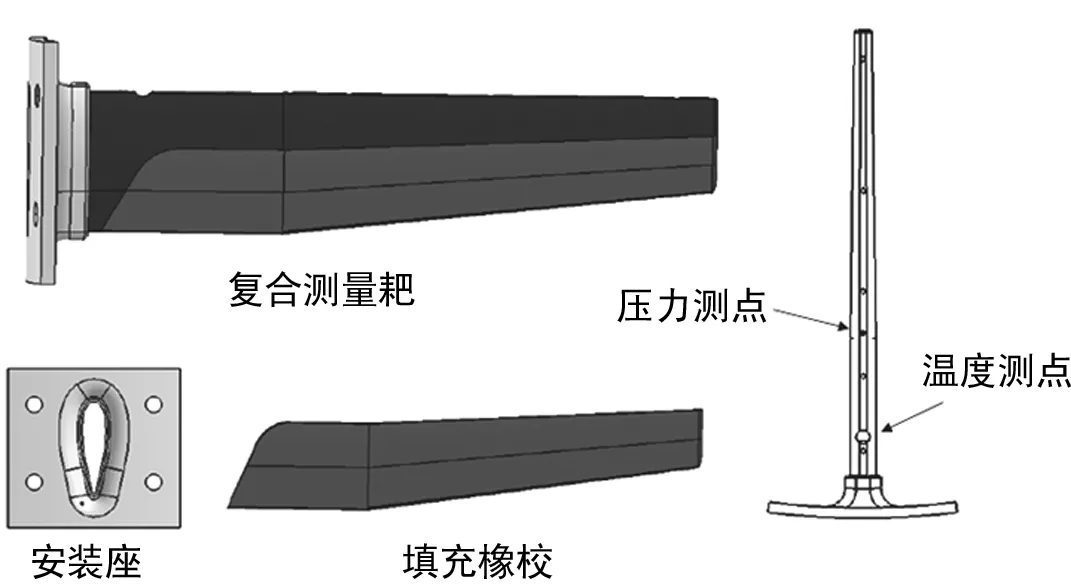
图1 某型发动机进气道测量耙结构示意图
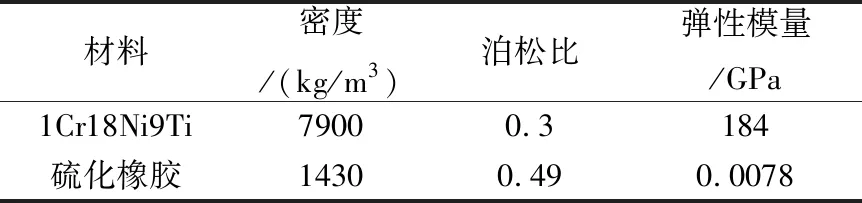
表1 填充材料参数
图2为测量耙实物图,从图中可以看出,在装机使用前的振动试验环节,测量耙耙体即出现了明显的裂纹(见图2左侧局部放大图标记位置,温度测点根部),为保障发动机飞行试验的顺利进行,需要对测量耙损伤原因进行分析,并设计出满足强度和寿命要求的测量耙。

图2 测量耙实物图
2 模态分析
测量耙安装于发动机流道内,受到发动机转子所产生的振动载荷,当测量耙的固有频率和气流的激振频率或转子的转动频率重合时,就会产生谐共振,造成耙体的损坏。模态分析[8]方法是获得测量耙固有频率,并进行其它线性动力学分析的基础,其有限元控制方程为:
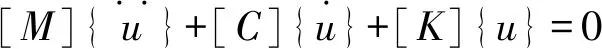
式中:[M]为总体质量矩阵;[C]为总体阻尼矩阵;[K]为总体刚度矩阵,在实际工程应用中,一般可以忽略阻尼,因此上式可以变为:
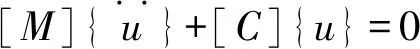
模态计算中,认为结构是线性的,即具有恒定的总体质量矩阵和总体刚度矩阵,因此可以假设上式的通解为:
消去时间变量后可得:
([K]-ω2[M]){φi}=0
不考虑无振动的情况,求解上式的特征值即可得到测量耙的振动频率,特征值对应的特征向量即为该频率下的振型。
针对测量耙出现的结构损伤问题,使用ANSYS软件对其进行模态分析,材料参数设置参考表1。以六面体网格为主进行网格划分,共划分215893个单元,886132个网格节点,有限元网格如图3所示。
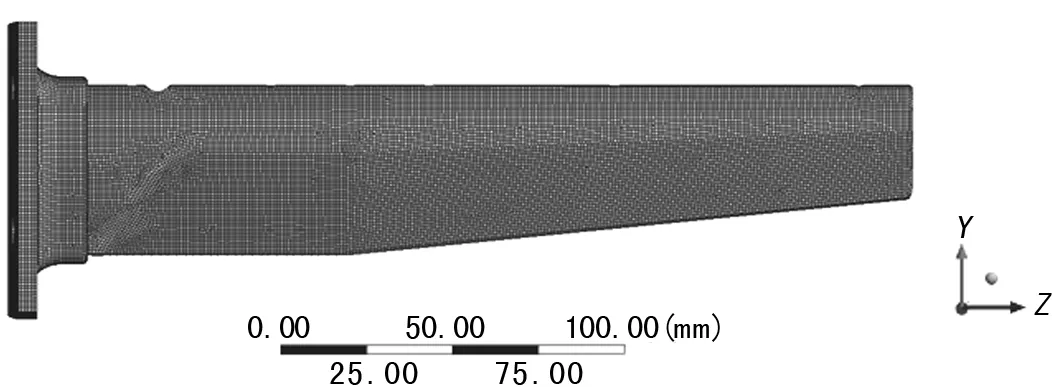
图3 有限元网格示意图
参考实际的测量耙固定方式,对测量耙底部四个安装孔壁面施加固定约束,将测量耙主体、安装座及填充橡胶之间分别建立接触约束。
为考核计算结果的可靠性和准确性,针对振动试验件,按照GJB150.16A《军用装备实验室环境试验方法 振动试验》中的要求进行地面环境试验,在10~2000 Hz频率范围内,以振动0.3 mm(10~40 Hz),加速度2g(>40 Hz)以上的正弦扫描振动进行1 h的共振检查,并在试验前后进行扫频,扫频结果及其与数值计算结果的对比如表2所列。
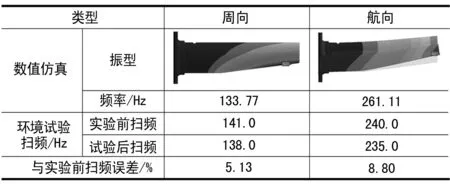
表2 数值仿真与试验结果对比
可以看出,数值仿真结果与环境试验扫频结果的误差不大于9%,验证了数值仿真结果的可靠性。同时,经过查询发动机相关技术文件,发现测量耙周向一阶固有频率与发动机某状态的转动频率重合,分析可得,测量耙与发动机产生的谐共振可能是导致耙体损伤的主要原因。
3 测量耙结构优化设计
结合上述分析可知,需要提高测量耙的固有频率以避开发动机转动频率,提高测量耙的可靠性,因此需要对其结构进行优化。结合现有研究[8-10]与理论分析可得,与测量耙的固有频率关系密切的变量包括测量耙长度、迎风面面积和材料属性等参数,其中测量耙长度受测点数量和分布的限制,材料种类受耙体所在工作截面工况、加工和制造成本的限制。综合考虑上述因素后,针对原有结构固有频率过低和根部损伤的现象,通过以下几个方面对测量耙进行加强:①加长测量耙根部主体不锈钢段,从21.17 mm增加到56.19 mm,同时提高测量耙主体支撑杆与安装座倒角面积,具体参数如图4所示;②在保证迎风面阻塞比满足要求(优化后的结构阻塞比3.51%,小于5%)的条件下,增加测量耙主体迎风面宽度,测量耙支撑杆根部最大宽度从15.19 mm提高到20 mm;③分析原有设计中测量耙主体根部受损的原因,可能是由于测量耙迎风面宽度较小且沿轴向宽度大导致测量耙沿轴向强度不足,因此在增加测量耙迎风面宽度的同时适当减小测量耙沿轴向的尺寸,从63 mm减小为60 mm。
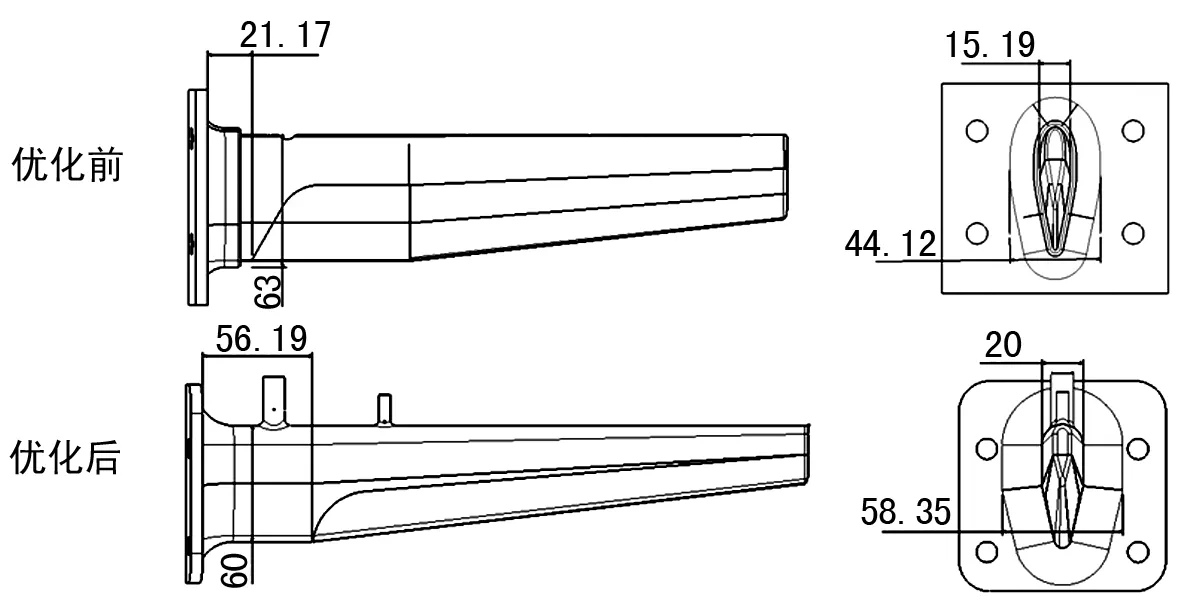
图4 优化前后测量耙结构参数对比
3.1 静强度分析
测量耙安装在发动机流道中主要受到的载荷之一为气动载荷,一般情况下,作用在测量耙上的气动阻力为:
式中:Cx为阻力系数,对于圆柱形Cx=1.2,对于矩形Cx=1.3,S为感受器的迎风面积。通过测量耙安装截面发动机流道参数计算得到该截面测量耙迎风面所受的压力为28 kPa,因此在ANSYS中对两种测量耙施加压力载荷进行静强度计算,其中结构优化后的测量耙同样采用六面体为主的网格划分方法,共划分233 352个结构单元,902 446个网格节点,计算后的两种结构等效应力分布分别如图5所示。
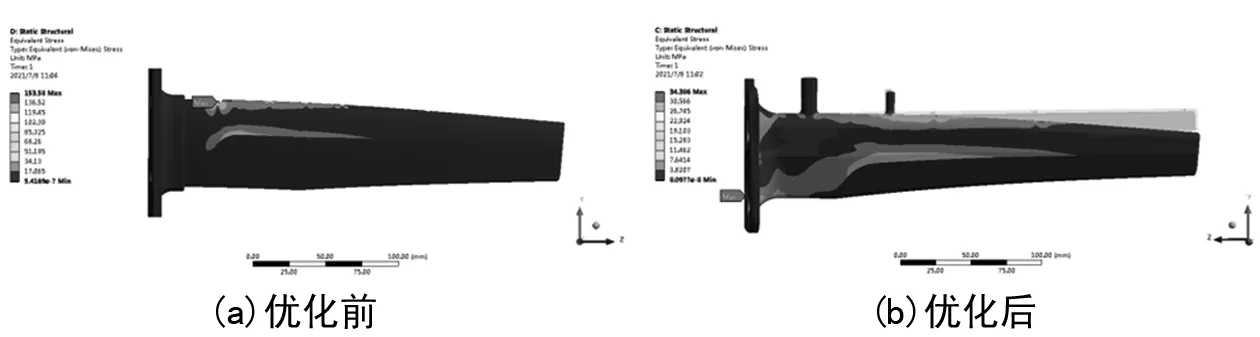
图5 两种结构静应力对比
为保证测量耙有足够的安全裕度,对于进气道出口的低温端测量耙,通常要求其安全系数ns>2,安全系数的定义为:
式中:σs为材料屈服应力,下标s表示残余应变,取0.2%;σmax为测量耙危险截面最大应力。查询材料手册得到1Cr18Ni9Ti不锈钢材料20 ℃下的屈服强度σ0.2=275 MPa,从图中可以看出,原有测量耙根部动态温度传感器测点位置处应力最大,经过计算,安全系数为275/158.83≈1.73<2,这与测量耙根部出现损伤的试验结果相符;优化后的结构安全系数为275/34.386≈8.0>>2,证明通过对测量耙根部加强和优化,应力分布得到显著改善,静强度满足设计要求。
3.2 模态特性数值分析
对优化后的几何结构进行模态分析,材料参数和固定方式与优化前的几何结构完全相同,计算得到的测量耙前六阶固有频率如表3所列。其中,第一阶和第二阶分别为测量耙沿发动机周向和轴向的一阶固有频率,其余几阶均为激发出的填充橡胶的局部振型,这是由于相比不锈钢材料,橡胶材料刚度较低,高阶振动时橡胶材料振动特性与主体骨架不同,因此优先激励橡胶材料振动。从表中可以看出,经过优化后的测量耙固有频率得到显著提高,并且成功避开了发动机的转动频率。

表3 优化后测量耙前六阶固有频率及振型
3.3 随机振动特性数值分析
固定安装座螺栓孔侧壁面,沿发动机周向对两种结构的复合测量耙按照GJB150.16A图C.16中涡轮发动机振动环境功率谱密度进行加载,模拟发动机随机振动,加载方式如图6所示。其中f0为发动机各状态高、低压转子转速,加载时尖峰值分别取高、低压转子转速的1倍和2倍,两种结构沿周向随机振动计算结果对比如表4所列。
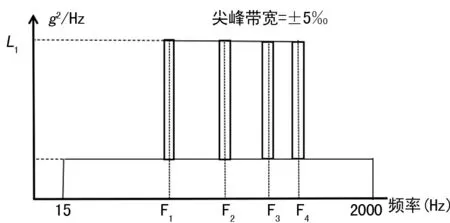
图6 随机振动环境功率谱密度
可以看出,3 Sigma(99.73%)概率下优化后的测量耙沿周向最大等效应力为59.771 MPa,相比原结构的543.64 MPa得到显著降低,分析原因可能是由于优化后测量耙固有频率提高,避开了发动机转子转速;另一方面,硫化橡胶具有良好的阻尼减振特性,优化后的测量耙横截面积增大,填充橡胶体积增加,同时与金属支撑杆接触面积增大,减振效果增强,从而降低了随机振动应力值。
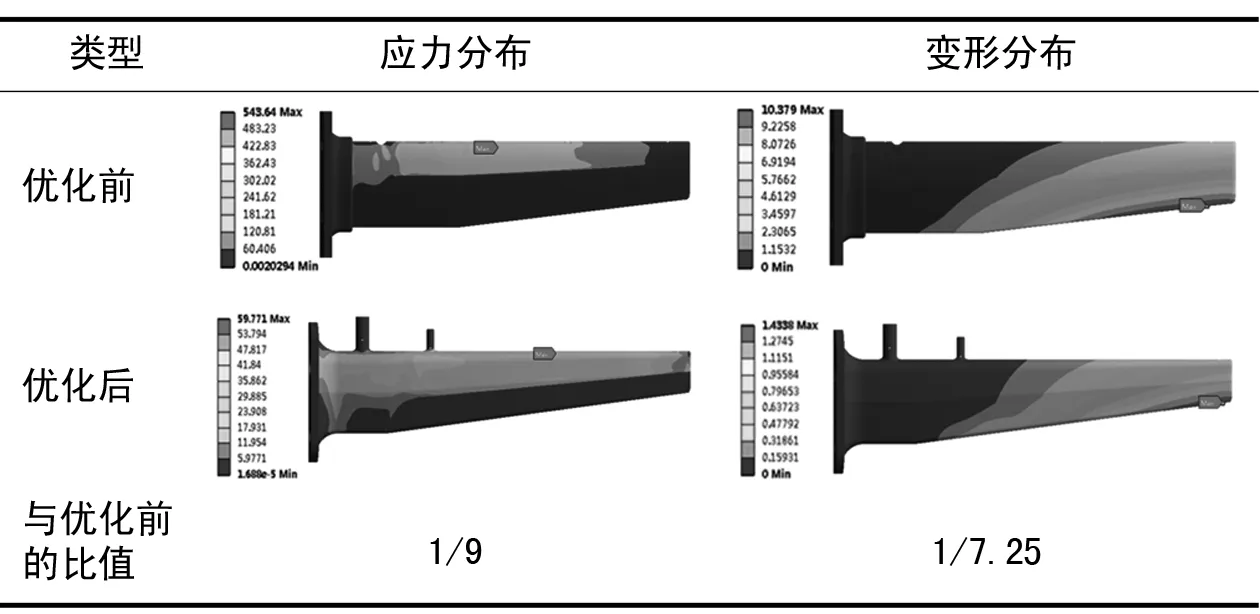
表表4 两种结构沿周向的随机振动应力及变形对比
3.4 试验验证
对改进后的测量耙进行地面环境试验,按照图6所示功率谱密度沿三个方向进行1 h随机振动强度考核,图7为试验件周向安装示意图,图8为实际加载的耐久振动试验控制图谱,图9、10分别为振动试验前轴向和周向的扫频结果。通过与表3中的模态计算结果比较可得,两个方向的一阶固有频率误差分别为8.66%和6.79%,验证了数值仿真方法的准确性,振动试验后样件外观检查良好,无裂纹等缺陷。优化前后两种测量耙模态对比如表5所列。
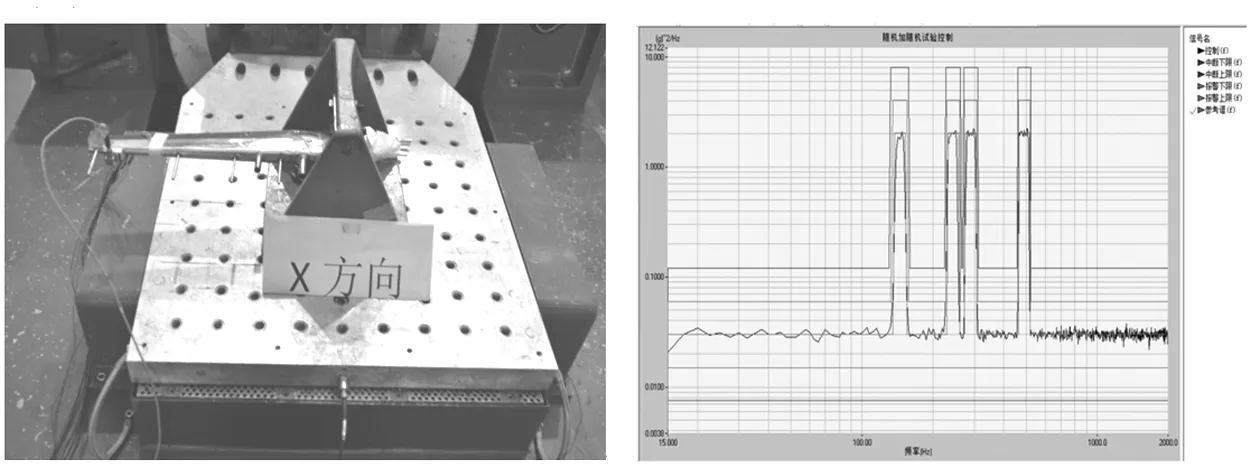
图7 试验件周向安装系统示意图 图8 耐久振动试验控制图谱
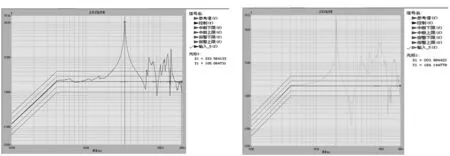
图9 轴向功能振动试验前正弦扫频控制及监测图谱 图10 周向功能振动试验前正弦扫频控制及监测图谱
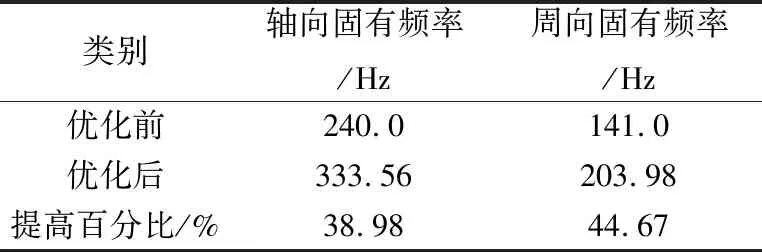
表5 优化前后测量耙固有频率对比
4 结 论
采用振动试验和数值仿真的方法对某型发动机进气道测量耙的损伤问题进行研究,并进行结构优化设计,经过研究,主要结论如下。
(1)对某型发动机进气道测量耙损伤进行试验和数值仿真分析,发现是由于其根部设计强度不足,导致测量耙固有频率与发动机转动频率重合,引发了谐共振使得测量耙受到的随机振动应力远超过该温度下不锈钢材料的屈服应力,从而产生了结构损伤。
(2)通过提高支撑杆底部钢结构段长度、增加测量耙迎风面厚度和安装座端面倒角尺寸等方式,显著提高了测量耙固有频率,将测量耙沿轴向和周向的固有频率分别提高38.98%和44.67%,成功避开发动机所有状态下的转动频率。
(3)经过结构优化,测量耙的静载荷和随机振动载荷得到显著降低,随机振动应力和变形分别减小为原来的1/9和1/7.25;针对改进后的测量耙进行环境试验验证,发现模态分析结果与扫频结果最大误差不超过8.66%,验证了本文使用的结构优化方法和数值仿真方法的可靠性。
(4)通过数值仿真和试验验证,证明优化后的测量耙结构满足该型号发动机试飞要求;同时,文中所提出的测量耙结构优化方法,可以为后期测量耙结构设计提供参考,计算方法可应用于后续测量耙设计及校核计算中。
