民营经济发展水平相关因素的稳健回归研究
2022-05-20杨联强叶梦琳程丹丹刘美月
杨联强,叶梦琳,程丹丹,刘美月
(安徽大学 数学科学学院,合肥 230601)
0 引 言
自改革开放以来,中国经济迅速发展,国内各种形式的一体化蓬勃兴起,各地区经济正在成为一个相互依赖相互联系的有机整体。然而中国东西部的区域经济发展出现较大的不平衡,主要体现在东部发展较快,但是中西部由于受地理位置的约束,造成经济发展迟缓,东部和西部的人均GDP和居民收入存在显著的差异。[1]以上市公司数量为例,中国上市公司主要集中在东部地区,中西部地区上市公司分布相对分散,数量上也呈现劣势。调查发现,中国各地区上市公司数量分布存在明显的阶梯型特点。[2]如何选取合适的计量经济方法,研究上市公司区域分布差异性,值得进行深入探讨。
民营企业是推动中国经济发展不可或缺的力量。例如,去年以来,中国民营上市公司积极应对疫情挑战,生产经营情况明显好于国有、外资企业,展现出较强的发展活力。民营企业具有收入增长快、营业成本低、效益恢复好、研发强度高、发展预期稳、公司规模小、易吸纳劳动力等特点。[3]从国有与民营企业对于区域人均财政收入、居民人均可支配收入、人均GDP三个维度衡量的区域经济贡献看,二者差异显著。国有企业仅在增值税对于区域人均财政收入影响方面优于民营企业,在所得税对于区域人均财政收入的影响和总资产对于人均GDP影响方面二者近似外,其它所有的解释变量均是民营企业优于国有企业。中国的民营企业不仅在微观效率上具有优势,在区域宏观经济的贡献方面,同样具有明显的优势。[4]
本文选取各省市民营上市公司数量为因变量,参照已有研究文献,测度区域经济发展程度的变量,可以从不同维度来衡量民营经济的贡献。经济增长是区域发展程度不可或缺的衡量维度之一,而民营企业的发展离不开一个地区的自然资源、社会资源、发达的交通,与企业相关的科学研究更是影响了企业发展的未来。故本文选取各省市区域面积、人口数、铁路营业里程、公路里程、电力消耗量、地级及以上城市数、城区面积、地区生产总值、R&D人员全时当量、R&D经费、R&D项目数、有效发明专利数、普通高等学校数、普通本专科招生数、普通本专科在校学生数、技术市场成交额等作为自变量来分析它们之间的相关性。[5]然而中国上市公司区域分布数量明显呈现不合理性,并且在某些地区过于集中在少数省、市,如广东和上海。在很大程度上会形成异常值或离群值,如果利用经典的均值回归模型,那么在计算过程中对每个观测值都赋予相同的权重,由此带来对异常值的处理不当,使回归系数估计产生较大偏差,从而大大影响回归模型的有效性。[6]另外,采用严格的稳健回归模型应用于全国各省市民营公司分布数量差异研究相对匮乏,这为本文提供了立题依据。鉴于此,本文将选择合适的计量经济模型时,加入模型稳健性的理论分析,并创新性的将合适的稳健回归模型应用于中国民营上市公司分布与区域要素的相关性分析上,从而排除异常值的过渡干扰,更可靠的揭示真实的相关性,为相关的政策建议给出更准确的数据分析结果支撑。[7]
1 中国地域民营经济发展水平相关因素研究
1.1 数据的描述性统计
市公司区域分布差异涉及多个方面, 本研究以2017年中国民营企业上市公司为例,从面积(x1)、人口数(x2)、铁路营业里程(x3)、公路里程(x4)、电力消耗量(x5)、地级及以上城市数(x6)、城区面积(x7)、地区生产总值(x8)、R&D人员全时当量(x9)、R&D经费(x10)、R&D项目数(x11)、有效发明专利数(x12)、普通高等学校数(x13)、普通本专科招生数(x14)、普通本专科在校学生数(x15)、技术市场成交额(x16)等多方面进行研究, 各变量的描述统计如表1。各自变量与因变量(y)之间的散点图如图1所示。
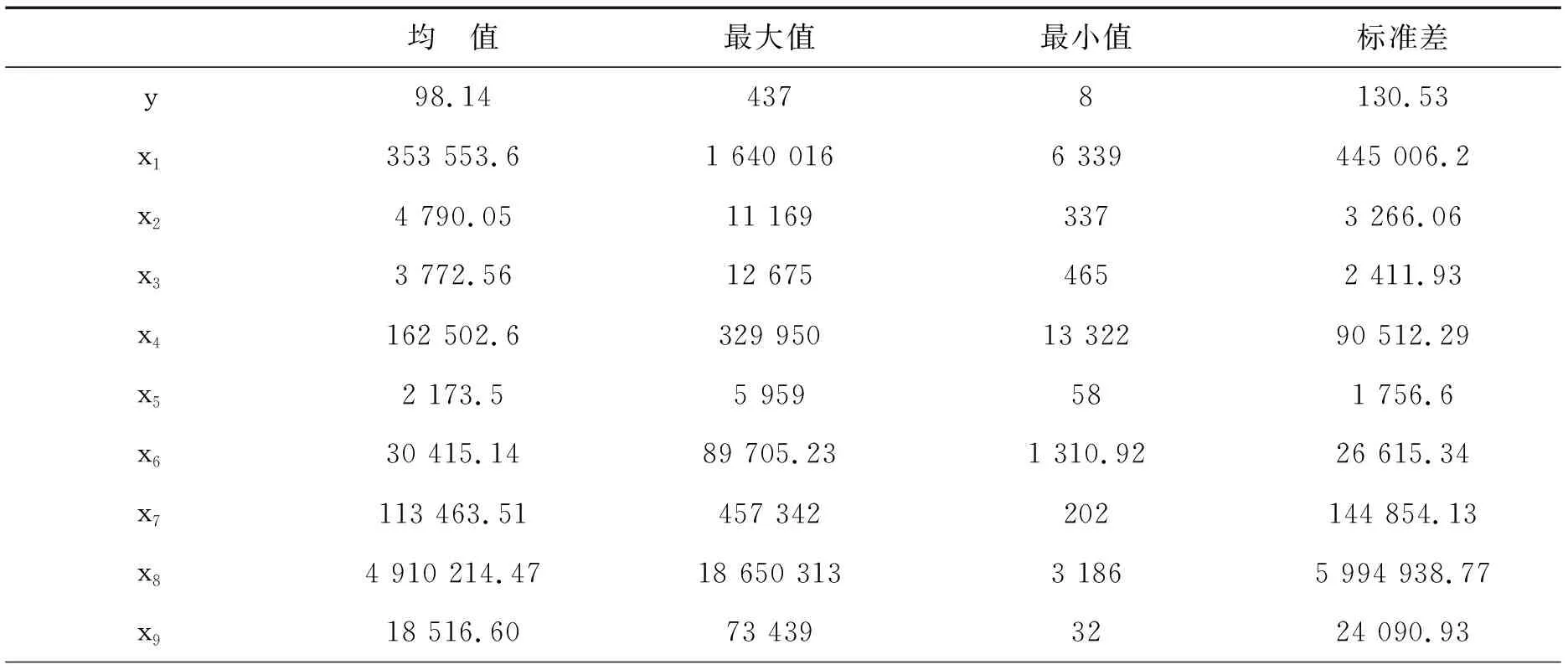
表1 各自变量描述统计量
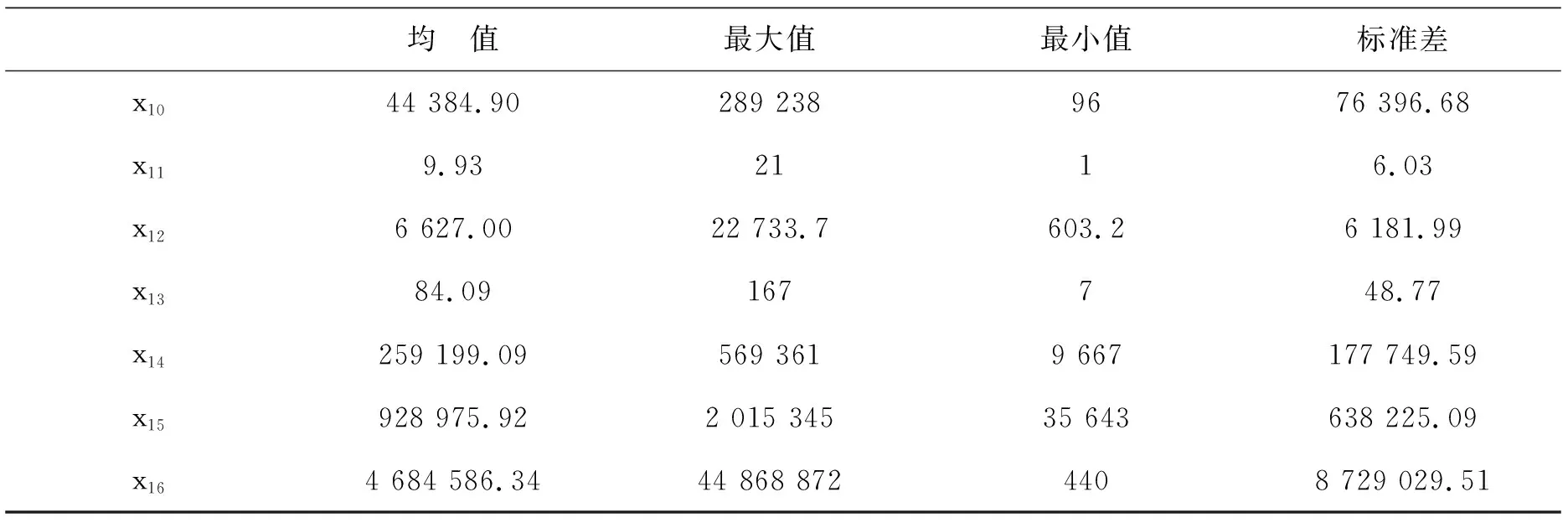
续表1 各自变量描述统计量
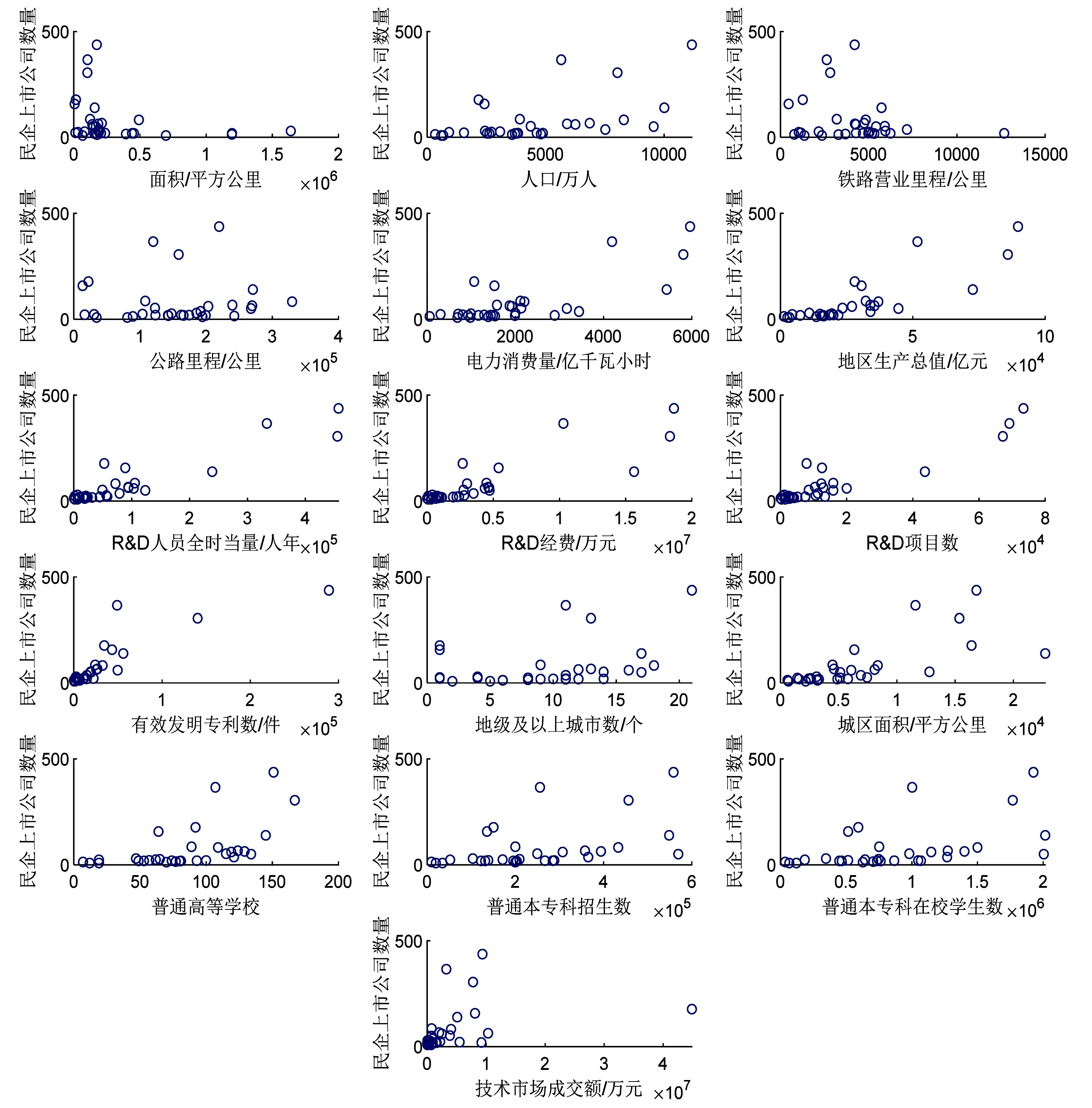
图1 变量间的散点图
本文的数据均来自中国统计年鉴,数据的分析、处理和计算均在SPSS 26.0中完成。
1.2 模型建立
稳健回归是基于异常值提出来的一种用于改良最小二乘估计的统计回归方法,它基于迭代最小二乘法在一定程度上减小了异常值对回归估计的影响,从而提高了回归模型的有效性。[11]对于一个因变量的变动与多个解释变量有关的线性模型,考虑分别用最小二乘估计和稳健回归模型来分析一般的多元线性回归模型。
1.2.1 最小二乘估计
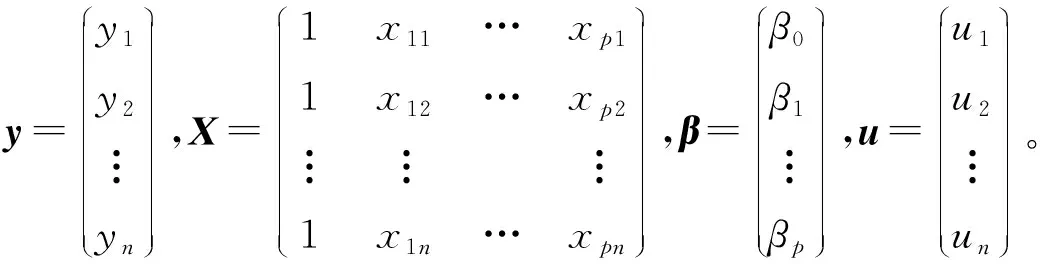
考虑模型
y=Xβ+u
最小二乘估计的目标函数为
最小化该目标函数可得正规方程组
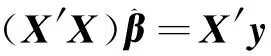
由此可以得到,最小方差无偏估计
大家知道,线性回归模型的上述最小二乘估计量,在噪声 服从高斯或次高斯分布的条件下,有着最优的估计效率。
1.2.2 稳健回归模型
线性模型的最小二乘估计虽然在一定条件下有着优秀的表现,但如果样本点存在异常值,此时采用最小二乘估计却会产生较大的偏差,也就是说该方法的稳健性不够。因此,再采用稳健回归模型对本文问题进行建模分析,看最终的结果有何差异。选取Huber损失函数
其中,c为调和常数,本文取c=1.345。
于是目标函数
(1)
极小化(1)式(即对β求偏导,并令其为零)可得:
令权重
于是
具体迭代步骤描述如下:
(1)取迭代初值:选取最小二乘估计的参数向量(X′X)-1X′y作为本次迭代的初值β(k);
(2)求初始残差:利用迭代初值计算初始残差ei=yi-Xiβ(k);
(4)令权重向量w=(w1,w2,…,wn)′,将其化成对角阵W=diag(w),带入β(k+1)=(X′WX)-1X′Wy,求得β1,进而求得新的残差与权重向量;
(5)再返回步骤(2),计算每一步迭代的β(k),若每一个估计值都满足:
则β(k+1)即为所求估计值(ε为预先设定的误差容忍度)。
1.3 模型估计结果分析
以民企上市公司数量为因变量,面积/平方公里, 人口/万人, 铁路营业里程/公里等为自变量,建立如上的多元线性回归模型,分别采用最小二乘估计和稳健回归拟合方程的系数,分析回归方程的显著性以及回归系数的显著性,观察在两种不同的方法下的差异性,从而理解稳健回归在处理异常值时的意义所在。下面比较最小二乘法与稳健回归下回归方程的显著性与回归系数的显著性。
由最小二乘估计分析结果可知,模型R2=0.971,意味着各省市面积/平方公里、人口/万人、铁路营业里程/公里等各解释变量可以解释民企上市公司数量的97.11%变化原因。
首先进行回归方程的显著性检验,发现在检验水平α=0.05的检验下模型通过F检验(F=29.450,p=0.000<0.05),即各省市面积/平方公里、人口/万人、铁路营业里程/公里等各解释变量至少有一项会对民企上市公司数量产生影响关系。
再进行回归系数的显著性检验,以各省市面积/平方公里为例:面积/平方公里的回归系数值为0.000,但是并没有呈现出显著性(t=0.210,p=0.837>0.05),意味着面积/平方公里并不会对民企上市公司数量产生显著影响关系。以此类推可以得到下面的结论:
面积/平方公里, 人口/万人, 铁路营业里程/公里等均不会对民企上市公司数量产生显著影响关系。(下面利用同样的方法进行分析,不再赘述)
然而观察数据表发现其中存在矛盾:数据表中可以看出地区生产总值高的地区民企上市公司数量较多,例如,上海、安徽、新疆的地区生产总值分别为30 632.99、27 018、10 881.96亿元,北京、安徽、新疆的民企上市公司数量分别为157、60、29所,综合表中数据可判断出地区生产总值对民企上市公司数量呈显著的正向影响。此外,R&D经费(全社会研究与实验发展经费)支出指统计年度内全社会实际用于基础研究、应用研究和实验发展的经费支出,即对经济发展产生间接影响。另外,由于研究具有不确定性,需要大量科学技术支持,常常无法带来盈利且需要花费大量费用。故R&D经费应对民企上市公司数量呈显著的负向影响。综上,由于上述分析与结论的矛盾性,考虑OLS分析在本次检验中的不准确性,因此,下面研究稳健回归分析在本次检验中的准确性。
由稳健回归分析结果可知,回归方程的显著性检验:在检验水平α=0.05的检验下模型通过F检验(F=24.861,p=0.000<0.05),即各省市面积/平方公里、人口/万人、铁路营业里程/公里等各解释变量至少有一项会对民企上市公司数量产生影响关系。
回归系数的显著性检验:由上表可知,地区生产总值/亿元、R&D项目数、有效发明专利数/件、技术市场成交额/万元会对民企上市公司数量产生显著的正向影响关系,R&D经费/万元会对民企上市公司数量产生显著的负向影响关系,面积/平方公里、人口/万人、铁路营业里程/公里、公路里程/公里、电力消费量/亿千瓦小时、R&D人员全时当量/人年、地级及以上城市数/个、城区面积/平方公里、普通高等学校、普通本专科招生数、普通本专科在校学生数不会对民企上市公司数量产生显著影响关系。
在本文中,地区生产总值/亿元、R&D经费/万元、R&D项目数、有效发明专利数/件、以及技术市场成交额/万元这几个解释变量在最小二乘估计下对民企上市公司数量没有显著性影响,而在稳健回归下对民企上市公司数量产生了显著性影响,这恰恰说明了稳健回归在处理异常值时的优良性,这种回归本身具有克服或消除样本数据波动性的功能,相较于最小二乘估计能够更好地拟合出被解释变量与解释变量的关系。
2 结论和建议
最小二乘估计与稳健估计的本质差异在于前者赋予观测值相同的权重,后者利用迭代最小二乘法减小异常值对回归估计的影响,从而认识到稳健回归在处理异常值时的优良性。
由模型分析结果了解到,地区生产总值/亿元、R&D经费/万元、R&D项目数、有效发明专利数/件、以及技术市场成交额/万元这几个解释变量在两种估计下对民营上市公司数量产生了不同的影响。从前文对解释变量的描述性统计中得知,地区生产力的发展与科技的进步对经济的影响是毋庸置疑的。显然在这组数据下,稳健回归的估计结果更加接近真实情况。
因此,在解决此类问题时,需要着重考虑对经济生产力与科学技术进步产生显著影响的解释变量,如果发现数据存在明显的异常值,采用稳健回归也许会得到较佳的结果。[11]综合本文分析结果,为了减小区域经济发展差异,促进各地协调发展,建议鼓励以科技创新驱动转型升级,助力区域跨越式发展;支持民营企业发展,促进区域协调发展;践行绿色发展理念,增强可持续发展能力。[12]
