基于最大层间位移的超高层结构黏滞阻尼器优化布置
2022-05-20尹思琦赵修明
尹思琦,赵修明
(1.天津城建大学 土木工程学院,天津 300384;2.天津城建设计院有限公司 建筑设计分院,天津 300384)
近年来,随着超高层建筑在我国的飞速发展,超高层建筑的抗震成为工程师们关注的问题之一.黏滞阻尼器可同时减少结构地震力和结构位移,且不会提供附加静刚度,这使它在超高层结构抗震中得到了广泛应用.自20 世纪80 年代,第三代黏滞阻尼器被发明并投入应用后,在工程上得到广泛认可[1],之后对黏滞阻尼器的研究皆基于第三代黏滞阻尼器.左秀国等[2]对某49 层框架核心筒结构在无控和布置黏滞阻尼器两种情况下进行地震反应对比分析,结果表明在多遇地震和设防地震下,布置黏滞阻尼器的结构可以对结构的层间位移和楼层剪力的地震反应有良好控制效果;魏宏亮等[3]对某37 层框架核心筒结构进行近场地震作用下的黏滞阻尼器减震分析,研究表明黏滞阻尼器在中震和大震下吸收了大部分地震输入能量,降低了结构构件损伤程度.
因黏滞阻尼器造价昂贵,故在结构设计时需要对其进行优化布置.徐正明等[4]提出基于POA 法的超高层框筒结构黏滞阻尼器优化方法,通过盈建科对无控结构进行静力分析,得出结构薄弱位置,在薄弱层布置阻尼器;另有研究者引入了智能算法,如燕乐纬等[5]提出基于相对适应度遗传算法、赖文龙等[6]提出基于模拟退火算法的优化方法,其中相对适应度遗传算法采用二进制编码,将布置阻尼器的单元编码1,无阻尼器单元编码0,可对布置阻尼器的结构进行有效模拟,故应用更广泛.
现有黏滞阻尼器优化布置研究基于静力推覆分析,本文在上述提出的优化布置方法基础上,以某超高层框架核心筒结构为例,以动力时程分析下得出的结构最大层间位移为控制函数,对文中两种黏滞阻尼器优化布置进行对比分析,提出最优布置方案并对其有效性进行验证.
1 基于最大层间位移的超高层框架核心筒黏滞阻尼器优化布置方案
本文提出的黏滞阻尼器优化布置基本思路:在确定黏滞阻尼器数目的情况下,找出使黏滞阻尼器达到最大减震效果的布置方案.
针对原框架核心筒结构,通过动力时程分析求出结构的地震响应,经过数据分析优选层间位移最大层,将黏滞阻尼器对称布置于该层.对已布置了黏滞阻尼器的结构进行第二次动力时程分析,以同样方法选出布置层.以此类推,直至全部阻尼器布置完毕.
为避免某层层间侧移过大产生塑性变形效应,理论上应尽量在竖向上每层均布置黏滞阻尼器.由现有研究可知,与竖向上逐层布置黏滞阻尼器相比,隔层布置更加经济有效[4].本文采取的优化布置方案需经过多次迭代计算,理论上其减震效果应优于隔层布置法,以下将通过工程案例对比分析两种布置方案的减震效果.
2 工程实例
2.1 工程概况
本案例工程为框架核心筒结构体系,地上30 层,总高108.6 m,首层4.2 m,标准层3.6 m.工程参数见表1,构件尺寸及材料等级见表2.
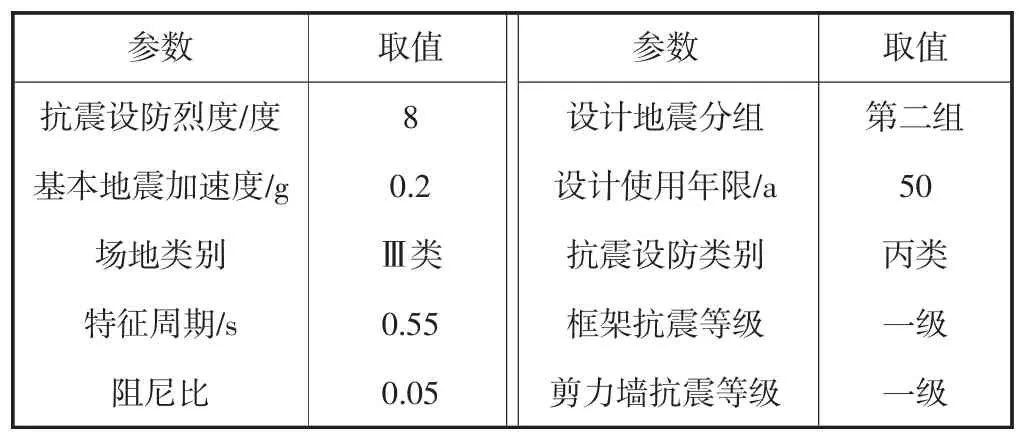
表1 工程参数

表2 构件尺寸及材料等级
用sap2000 对结构进行建模,建模过程:
(1)建立轴网.
(2)根据表2 所示构件尺寸及材料等级,定义材料属性和构件截面属性.纵筋选用HPB400,箍筋选用HPB300.建立钢筋和混凝土本构关系,混凝土使用Teked 滞回模型,钢筋使用随动滞回模型.其中,梁、柱采用框架单元,剪力墙采用壳单元,楼板采用膜单元,阻尼器采用阻尼器单元[7].
(3)绘制构件,建立结构几何模型.
(4)设定边界条件,选取地面(z=0 处)所有节点,指定约束类型为固接,剖分面单元,指定最大剖分尺寸为1 m.
这丫头怎么在这?难道她是潜伏到天南星妖身边,想伺机偷走海金沙吗?可就凭她那点仙力,根本不是天南星妖的对手,很容易偷鸡不成蚀把米。
(5)施加荷载,恒载(软件自动计算自重):屋面恒载2 kN/m2,楼面恒载4 kN/m2,结构边梁线荷载5.0 kN/m.活载:屋面活载0.5 kN/m2,楼面活载2.0 kN/m2.
(6)定义质量源,自重和附加恒载的系数为1.0,活荷载的系数取为0.5.
(7)塑性铰设定,框架梁设置M 铰,框架柱设置纤维铰,剪力墙设置分层壳.
(8)在楼板定义刚性隔板.
(9)定义地震波时程函数,建立荷载工况,动力时程分析取直接积分,阻尼系数设置选择按周期指定阻尼第一周期0.1 s,阻尼比0.3,第二周期0.01 s,阻尼比0.668[8].
结构平面如图1 所示,结构3D 模型如图2 所示.
2.2 黏滞阻尼器选型
2.2.1 黏滞阻尼器恢复力模型
阻尼系数C(ω)为
式中:C0为频率等于0 时的线性阻尼系数;k2为耗能刚度;ω 为频率;λ 为放松时间系数.
由式(1)可知,阻尼系数C 与频率ω 相关,具有频率依赖性,C(ω)/C0随频率的增大而减小.
2.2.2 黏滞阻尼器参数及平面布置
本工程依据文献[10]并结合工程实际选取阻尼器OPT 200/250,其参数见表3.

表3 黏滞阻尼器参数
阻尼器平面布置应遵循对称原则,每层布置8 个阻尼器,布置方式如图4 所示.
2.3 选取地震波
根据《建筑抗震设计规范GB50011—2010》中的相关规定,本文选用两条实际地震波和一条人工合成波进行罕遇地震下的动力时程分析.依据文献[11]中提到的选波原则,用SeismoMach 软件对PKPM 地震波库中的地震波进行选取,选出了三条符合要求的地震波.其中,两条天然波为EMC 波和LWD 波,一条人工波为兰州波,三条波如图5 所示.
3 计算结果与分析
3.1 模态分析
sap2000 模态工况取前100 阶振型进行模态分析,结构前5 阶振型周期如表4 所示.因结构具有对称性,故结构第一、二阶模态相同,第四、五阶模态相同.其中第一阶为平动,周期2.22 s,第三阶为平面扭转,周期1.15 s,扭转振型与平动振型比值为0.52,小于0.9,符合抗震规范[11]的要求.

表4 结构前5 阶振型周期s
3.2 黏滞阻尼器的优化布置分析
基于本文案例工程,拟考虑两种布置方案,并与原结构进行对比,两种方案分别为:
方案一,隔层布置黏滞阻尼器,共布置15 层.
方案二,以本文第2 节中提到的优化布置方案选择其中的15 层布置黏滞阻尼器,经计算得出布置层数为13~27 层.
通过sap2000 计算出结构在兰州波作用下的地震响应,结果如图6 所示.
从图6 可见,在兰州波作用下,两种方案均能大幅度减少地震响应.方案二对结构的最大层间位移减少率高达39.19%,对结构基底剪力减少率可达27.21%,分别优于方案一的35.33%和24.83%(见表5).
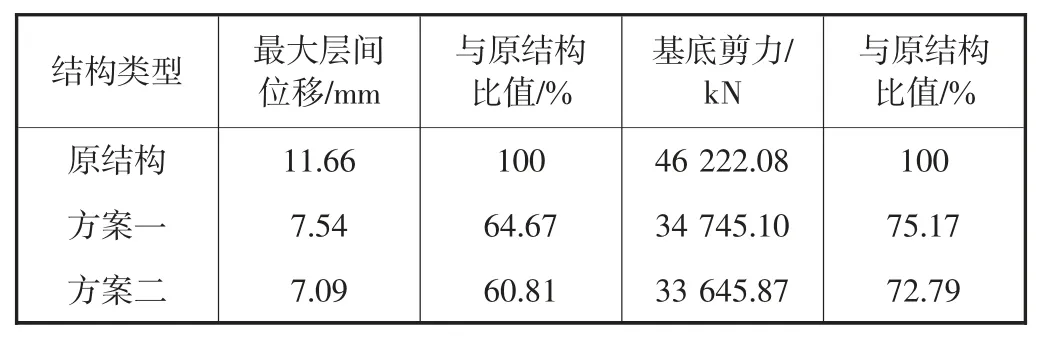
表5 兰州波下各方案最大地震响应
在EMC 波作用下,结构的地震响应如图7 所示.
与兰州波相比,EMC 波作用下的结构地震响应,层间位移减小、层间剪力增大.两种方案皆对层间位移有大幅度削减,方案一、方案二分别削减了31.61%和40.39%的层间位移.而对于层间剪力,两方案的减小率分别为13.67%和12.43%,仅相差1.24%,基本相当(见表6).
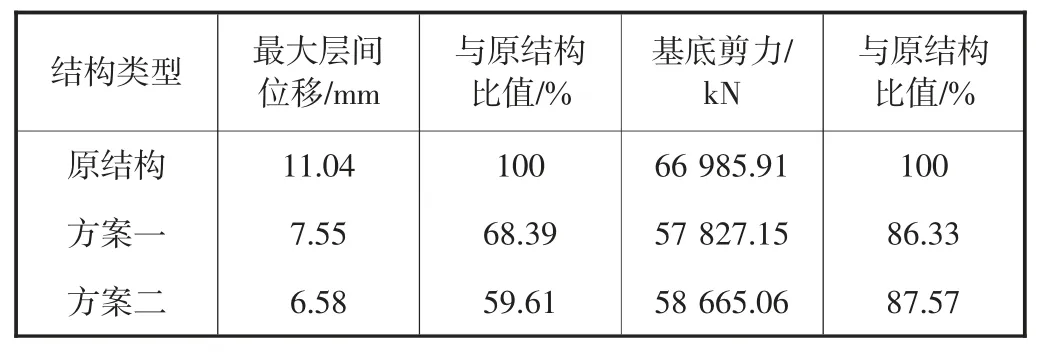
表6 EMC 波下各方案最大地震响应
在LWD 波作用下,结构的地震响应如图8 所示.
与兰州波相比,LWD 波作用下的地震响应,结构的层间位移和层间剪力皆增强.两种方案下的层间位移依然有大幅度下降,方案一、方案二分别削弱了37.88%和43.19%的层间位移.对层间剪力的减少率,两方案分别为14.38%和12.11%,依旧相差不大(见表7).

表7 LWD 波下各方案最大地震响应
基于上述地震响应对比分析,对于结构层间位移,方案二明显优于方案一;对于结构层间剪力,兰州波下方案二的减小率比方案一高2.38%,EMC 波和LWD 波下方案二的减小率分别比方案一高1.24%和2.27%,两方案相差不大.综合比较下,方案二基于最大层间位移法的黏滞阻尼器优化布置方案更优.
本文算例为30 层无偏心对称框架核心筒结构,在优化过程中发现,在三条地震波作用下对结构进行第一次动力时程分析,得出最大层间位移皆出现在第27 层,此后计算的层间位移最大层皆依次下降1 层.
4 结论
布置黏滞阻尼器能有效降低地震响应,提高结构的抗震性能.其中,黏滞阻尼器对层间位移的控制效果要明显高于对层间剪力的控制效果.
在确定黏滞阻尼器布置数量的前提下,本文提出的基于最大层间位移法优化布置方案要优于隔层布置方案.
当实际工程接近本案例时,可以选取第一次动力时程分析下的薄弱层进行布置,若仍需布置,则以此层为基准依次向下布置.
本文的优化布置方案只有层间位移做控制函数,同时考虑其他地震响应和阻尼器参数的变化,是否会得出更优布置方案有待进一步研究.
