双幅曲线连续钢-混组合箱梁剪力滞效应的研究

黄海兵， 刘 凡， 袁晓静

（1.苏州科技大学 土木工程学院，江苏 苏州 215011； 2.苏州科技大学 江苏省结构工程重点实验室，江苏 苏州 215011）

钢混组合箱梁兼具钢材和混凝土的材料性能优势，具有抗扭刚度大、承载力高、自重轻、施工快速方便等优点[1-2]。 曲线钢混组合箱梁目前已广泛应用在城市高架桥和人行天桥中，组合箱梁在对称荷载作用下产生挠曲时会发生剪力滞后的现象，称之为剪力滞效应。 由于剪力滞效应的存在，使得组合梁内的应力并不是均匀分布，往往会引起应力高度集中，从而导致安全隐患。

国内外对于曲线箱梁剪力滞效应已有了一定的研究[3-6]，但对于复杂截面的曲线组合梁[1]剪力滞效应的研究相对较少。 杨秀珍等对连续曲线钢箱梁进行了有限元分析研究，得出了曲率半径对曲线钢箱梁剪力滞效应的影响规律，曲率半径越小，截面剪力滞效应越明显，并且曲梁内外侧的剪力滞系数差异越大[7-8]；肖敏和李新平对连续曲线混凝土箱梁进行了有限元分析，探究了曲率半径和宽跨比对三跨曲线混凝土箱梁剪力滞效应的影响，发现曲率半径越大，截面内外侧剪力滞系数差距越小，当曲率半径大于300 m 时，截面剪力滞系数已与直梁相近[9]。

但已有的关于箱梁桥剪力滞效应的研究大多针对混凝土箱梁或钢箱梁，且直梁偏多，研究方法主要是数值分析和有限元模拟，缺少相应的试验研究。 目前，钢-混组合箱梁桥的应用越来越广泛，相关的试验研究却较少，因此本文就不同曲率半径对复杂截面双幅曲线连续钢-混组合箱梁剪力滞效应进行了试验研究，得到了有内外高低差的双幅曲线连续钢混组合箱梁不同截面的剪力滞效应分布规律。

1 试件设计

本文基于杭州绕城双幅曲线连续钢-混组合箱梁桥的工程背景， 以曲率半径为参数， 设计了2 个两跨钢-混组合曲梁试件，其中CCB-1 曲线梁的曲率半径为26 m，CCB-2 曲梁的曲率半径为52 m。 各试验梁参数见表1 所列。

表1 试验梁参数

每个试验梁横截面尺寸及材料均相同。组合梁计算跨度为4.5+4.5 m，一端设置固定铰支座，中间横隔板下设置活动铰支座，另一端也为活动铰支座。 各组合梁中的钢梁均为开口箱型截面。 整体宽度为1 370 mm，整体高度294 mm，桥面板承重结构采用80 mm 厚的现浇混凝土板，混凝土板宽为1 370 mm。 钢梁总高为214 mm，上翼缘宽度均为60 mm，下翼缘宽度均为430 mm，腹板厚度均为6 mm，翼缘厚度均为6 mm，两箱钢梁跨中间距670 mm，组合梁内外箱高差270 mm。 钢梁与混凝土之间采用栓钉连接，栓钉直径13 mm，长50 mm，属于完全连接形式。 钢梁材质为Q345D，混凝土强度等级为C50，组合梁截面示意图见图1。

图1 组合箱梁截面示意图

2 加载与测量

加载设备为两个5 000 kN 液压千斤顶，两个钢垫梁。 加载点均是两跨的中点。 试验现场图如图2 所示。由于是两跨对称梁，取其中一跨进行测试，并在另一跨设置对照截面，测试位置示意图见图3，其中左L/4 截面和左L/2 截面是测试截面，右L/2 和L/4 截面是对照截面。 测点布置在钢底板、钢腹板以及混凝土板上，布置示意图见图4。

图2 试验现场图

图3 测试位置图

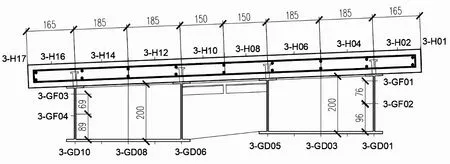
图4 测点布置图

3 试验结果分析

当与腹板交接处的翼板正应力值大于按初等梁理论计算的值时，称之为正剪力滞，反之称为负剪力滞。用剪力滞系数来反映剪力滞效应的严重程度，它代表着翼板应力分布的不均匀程度，剪力滞系数λ，即

已有的关于钢混组合曲梁剪力滞效应的研究更多的是在弹性阶段，本文考虑到组合梁进入塑性阶段后的应力更能体现实际工程中要求的最大应力状态，因此选取试验梁刚进入塑性阶段的荷载815 kN 下的各测试截面进行分析，并把高的一箱的外腹板称为外侧，低的一箱为内侧。

图5 给出了CCB-1 和CCB-2 试件左L/4 截面上混凝土板与钢梁底板的剪力滞系数。 从图5（a）可以看出，CCB-1 和CCB-2 的左L/4 截面上混凝土板的剪力滞系数均是内测大外侧小， 在混凝土翼板与腹板交接处均是负剪力滞，两箱均是外侧负剪力滞更严重，CCB-1 最大负剪力滞系数为0.59，CCB-2 最大负剪力滞系数为0.79，这是由于组合梁内外高低差的存在，在L/4 截面处较低的内侧混凝土的压应力相比外侧更大。 整体上，CCB-2 的剪力滞系数分布曲线要比CCB-1 平缓得多，CCB-2 的左L/4 截面上混凝土板的应力分布更加均匀。

从图5（b）可以看出，CCB-2 的左L/4 截面钢梁底板的剪力滞系数与CCB-1 相比差异较大，CCB-2 的最大正剪力滞发生在外箱外侧的1 号测点，最大剪力滞系数为1.11；而CCB-1 的最大正剪力滞发生在中间偏外侧的2 号测点上，最大剪力滞系数为1.2，这是因为CCB-1 的弯扭较大，致使钢底板最大应力位置产生了偏移。整体上，CCB-2 各箱底板剪力滞系数基本呈线性分布，且与CCB-1 相比更加平缓。上述CCB-2 曲率半径大，弯扭耦合效应比CCB-1 小，截面正应力受剪切应力流的影响就相对较小。 表2 列出了组合梁L/4 截面翼板与腹板交接处的剪力滞系数，并按由外到内依次命名为外箱外侧、外箱内侧、内箱外侧、内箱内侧。

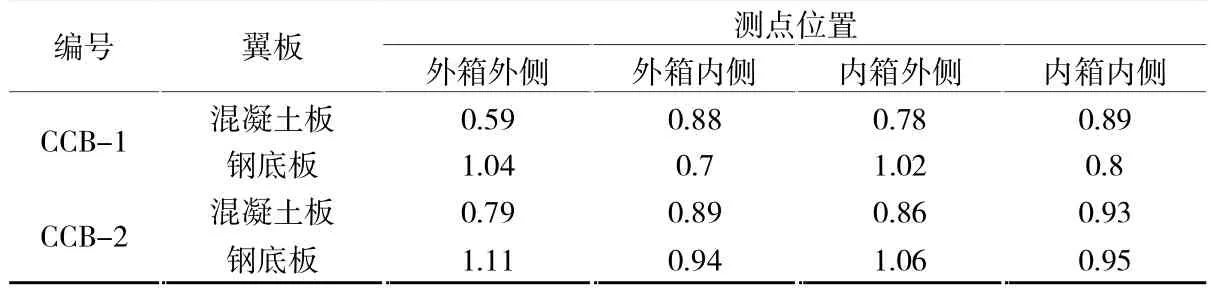
表2 L/4 截面翼腹板交接处剪力滞系数

图5 CCB-1、CCB-2 试件左L/4 截面剪力滞系数图

图6 给出了CCB-1 和CCB-2 试件左L/2 截面上混凝土板与钢梁底板的剪力滞系数。 从图6（a）可以看出，CCB-1 和CCB-2 的左L/2 截面上混凝土板的剪力滞系数分布也是外侧大内侧小， 在混凝土翼板与腹板交接处均是正剪力滞，两箱均是外侧正剪力滞更严重，其中CCB-1 最大正剪力滞系数为1.46，CCB-2 最大正剪力滞系数为1.26，这一点与L/4 截面处相反。整体上CCB-2 混凝土翼板的剪力滞系数分布更加均匀。从图6（b）可以看出CCB-2 的各测点剪力滞系数差值比CCB-1 小，CCB-1 和CCB-2 的各箱底板内侧剪力滞系数差异较大，CCB-1 为负剪力滞，剪力滞系数为0.96，而CCB-2 为正剪力滞，剪力滞系数为1.03。 两箱钢底板最大负剪力滞均发生在中间偏内测的第4（9）号测点。 造成上述现象的原因有两点：一是CCB-2 的曲率半径大，截面正应力分布相对较均匀；二是由于截面内外箱高低差的存在，加剧了曲梁的弯扭耦合作用。表3列出了组合梁L/2 截面翼板与腹板交接处的剪力滞系数，并按由外到内依次命名为外箱外侧、外箱内侧、内箱外侧、内箱内侧

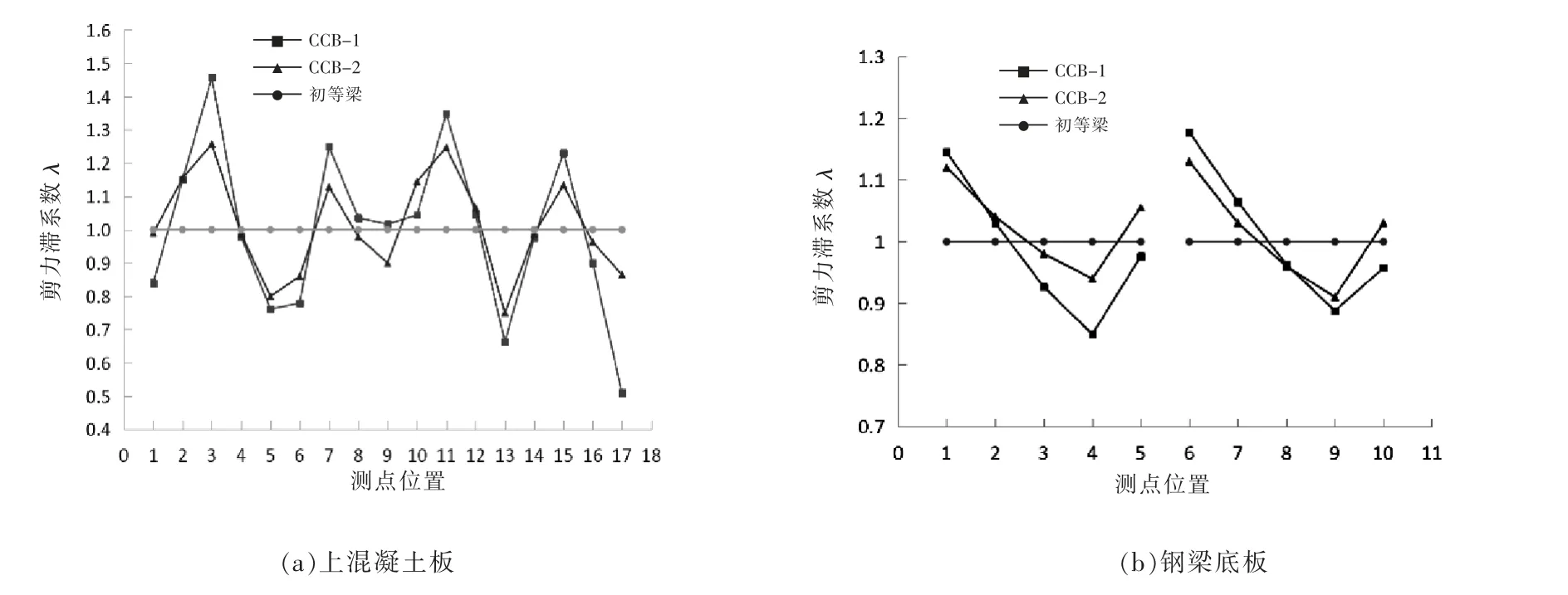
图6 CCB-1、CCB-2 试件左L/2 截面剪力滞系数图

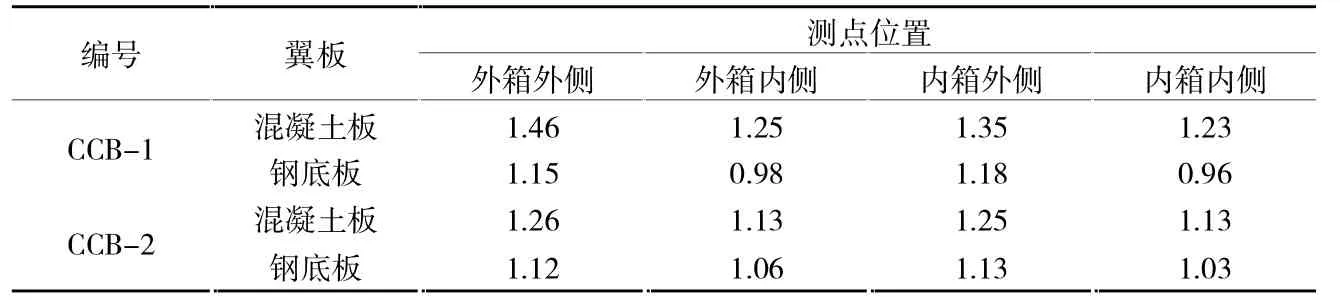
表3 L/2 截面翼腹板交接处剪力滞系数

综上所述，曲率半径对钢混组合梁的剪力滞效应影响较大，曲率半径越大，内外侧剪力滞系数差值越小，截面应力分布越均匀。从图5、图6 均可以看出组合梁钢底板的剪力滞效应要比混凝土板的剪力滞效应小得多。 对于有内外高差的复杂组合截面，曲梁的弯扭耦合作用会更大，剪力滞效应也越明显，甚至出现CCB-1和CCB-2 各箱内侧剪力滞相反的情况，这一点在实际工程中不容忽视。 从文献[9]、[11]和[12]中可以看出，截面形式对称的直梁剪力滞效应是对称的，而本文曲梁的剪力滞效应会偏向一侧。 而且曲率半径越小，组合曲梁剪力滞效应越大，内外侧剪力滞系数差值越大，截面应力分布越不均匀。 因此，在实际工程中形如高架桥出入口的弯车道要特别注意剪力滞效应的影响。

4 结论

通过试验研究，可得到以下结论：

（1）对钢混组合曲梁而言，考虑剪力滞效应是十分必要的。 从试验结果与初等梁理论结果的对比中可以看出，若不考虑剪力滞效应会严重低估组合梁中实际的应力，特别是在翼板与腹板交接处的应力，考虑剪力滞效应值是初等梁理论值的1.46 倍，在实际工程中很可能会发生过早地屈服，造成安全事故。

（2）有内外高低差的组合曲梁剪力滞效应更严重，这说明在实际工程中要针对不同的组合曲梁截面形式进行具体分析，找到最大应力处，避免意外发生。