地震灾害下埋地管道的有限元分析
2022-05-20姜志达吴玉国
姜志达,王 岳,吴玉国
(辽宁石油化工大学石油天然气工程学院,辽宁抚顺 113001)
我国是一个地震多发的国家,许多埋地管道在地震中受到了不同程度的损害,对自然环境和社会经济都造成了严重的影响,并且还诱发了许多次生灾害,因此地震对埋地管道存在较大的威胁,影响埋地管道的安全[1]。当地震发生时,土壤的变形会引起管道的压缩、变形、开裂等一系列现象,还可能导致漏油、管道停运,甚至火灾、爆炸等灾害,所以必须清楚地认识到这种地质灾害的危害性[2]。地震造成的危害是所有自然灾害中最大的,地震的发生不可预测,往往瞬间产生巨大的破坏,还伴有洪水、火灾等次生灾害,对人类的安全和经济造成巨大的损害。埋地管道的安全运行在可持续发展的经济体系中发挥基础性的作用,在其遭受破坏时,埋地管道抗御灾害的能力成为评价一个城市或地区抗击灾害能力的重要标志之一。若在一场地震灾害中能保护埋地管道的安全,或灾害后能快速恢复埋地管道的输送能力,将对社会的减灾工程和经济复苏起重要作用。因此,最大幅度地降低地震对埋地管道的危害,已经成为众多学者所面临的重大课题[3]。
目前,我国埋地管道输送油气的产业正处于高速发展的阶段,地震对埋地管道的影响直接关系到人类赖以生存的油、气等资源,造成管道的停运、停产,甚至造成很严重的火灾、环境污染等次生灾害[4]。地震的产生是独立于人类的意识而客观存在的,到目前为止人类都无法准确地预测地震产生的机理、时间、地点和强度,所以在地震造成损害之前需要采取一定的措施,在一定的程度上减轻地震造成的损害。埋地管道遭受地震的破坏,往往是由发生地震时的地层沉陷、土壤液化、地层裂缝错位引起的[5]。针对真实存在的地震波,本文研究了不同程度的地震波对埋地管道造成的损害,以期在埋地管道受到损害前提前采取抵御地震灾害的有效措施。
根据历代学者的研究可知,埋地管道在地震波作用下的理论模型一般分为两种:第一种是利用弹性地基上的连续梁进行分析,把土体设定为弹簧,用来描述土体对管道的作用,认为土体和管道发生相对运动;第二种是假设管线被埋在半无限空间中,土介质是线弹性介质,建立管道-土体联动方程。学者们的一系列可靠研究表明,第一种模型比较简单,计算比较方便,但是模型与实际情况存在较大差异;第二种模型是比较符合实际情况的模型,但是计算比较复杂,难以得到准确的结果。结合实际情况、管道高速发展的现状以及对管道安全运输的要求,建立符合实际情况的埋地管道模型是一个需要解决的重要问题。本文采取第二种建模方法,建立管道与土体间的接触模型[6-8]。
1 管道-土体有限元模型
1.1 结构参数
首先,运用ANSYS中的建模功能,建立埋地管道的管道-土体有限元模型。管道和土体均选用Solid186单元。Solid186单元是六面体20节点的单元,主要用于三维实体单元中,其特点是存在塑性、蠕变和膨胀等,节点的自由度分为U X、U Y、U Z三个方向,适用于大变形和大应变等情况。采用Solid186单元能够更精准地划分网格。管道选用最有特点的、使用最广泛的材料,选用管道的参数见表1;土体参数见表2;管道-土体模型如图1所示。
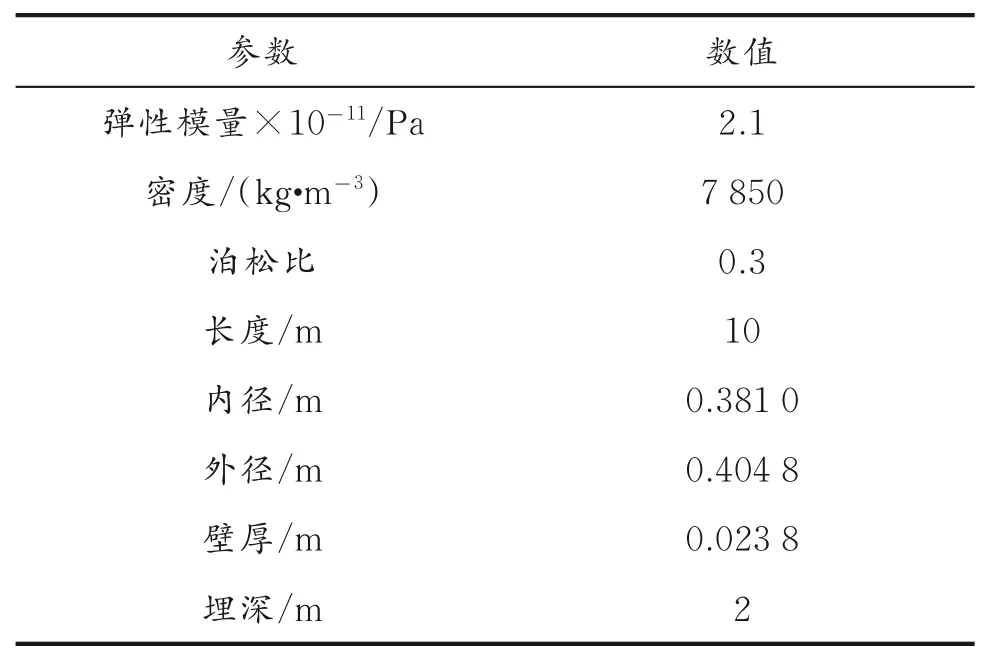
表1 选用管道的参数
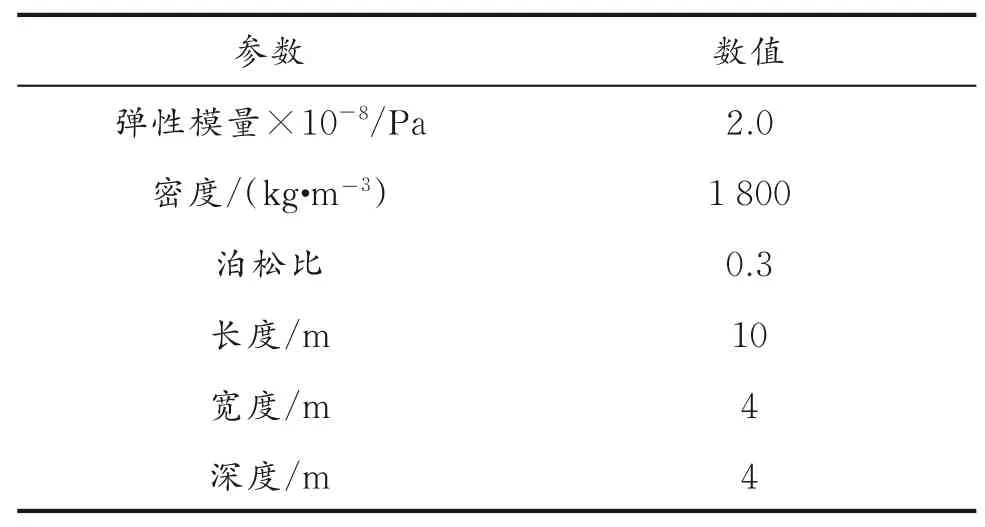
表2 土体参数
图1 管道-土体模型
1.2 几何模型及网格划分
建立管道与土体的几何模型,然后对模型进行单元网格的划分,使其成为有限元模型。如果网格划分恰当,则可使计算更加简便,在这一步需要确定单元属性和单元尺寸。利用ANSYS软件中的网格划分工具,对网格进行尺寸控制。本文主要研究管道与土体之间的相互作用,所以需要将管道划分为较小的单元,而土体可以划分为较大的单元。
划分单元时将管道一周划分成20份,长度划分成50份,结果见图2(a);土体的宽和深都划分成20份,土体的长划分50份,结果见图2(b)。网格划分后,总共生成24 950个单元、103 817个节点。
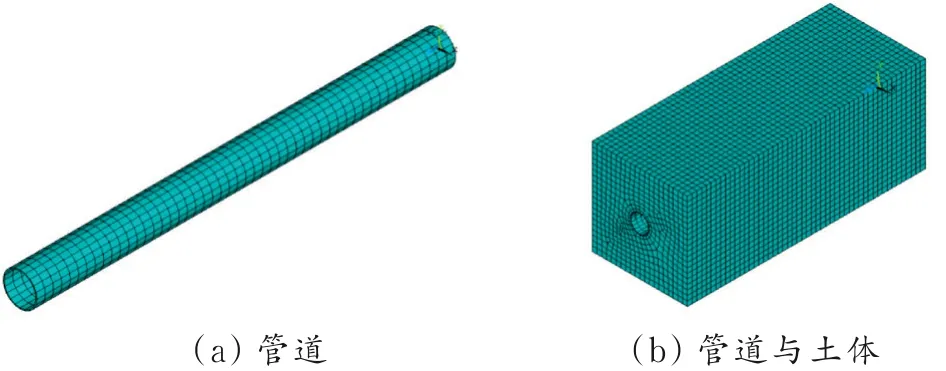
图2 网格划分
1.3 管道-土体接触模拟
在地震波的作用下引起埋地管道各种损坏和变形的主要原因是管道周围土体的相互作用,因此研究地震灾害对埋地管道力学响应分析的关键在于创建管道与土体间的接触模型[9]。在地震荷载施加过程中,土体与管线交界面上可能产生相对位移,因此需要利用ANSYS在管道与土体间创建接触对,在设置过程中需要选择接触面和目标面。利用ANSYS中的contact pair来定义管道与土体间的接触对,在此需要选择柔体-柔体的接触原则,把刚性较大的面定义为目标面,也就是把管道的外表面作为目标面,把刚性较小的面定义为接触面,也就是土体与管道的接触面[10]。管道的接触单元如图3所示。摩擦系数选择0.5。为了使计算更加简便地趋于收敛,在ANSYS计算中可以适当增加接触刚度并减小穿透容忍。同时,接触问题也是非线性问题,为了确保计算的收敛,可通过放松非线性收敛准则(CNVTOL)、增加荷载步数(NSUBST)、增加每次计算的迭代次数(默认为25次,NEQIT)等方法加以改进[11]。
图3 管道的接触单元
1.4 载荷的施加
首先,确定管道与土体模型的分析类型,ANSYS的分析类型包括静态分析、模态分析、瞬态分析、调谐分析和谱分析。根据研究对象,开始时选用静态分析,在施加地震波时改用瞬态分析[12]。
施加载荷是有限元分析中最为关键的步骤之一,ANSYS的载荷类型包括位移载荷、集中载荷、面载荷、体积载荷、惯性载荷和耦合场载荷。本模型首先定义时间位移载荷(DOF约束),在这一步对模型的空间自由度进行约束。由于模型处于半无限的空间中,在管道轴向的前后两个面和土体的前后两个面施加Z方向的约束,在土体上下两个面施加Y方向的约束,土体左右两个面施加X方向的约束;然后,施加面载荷,面载荷是均布载荷随线性变化的载荷,在管道的上方施加80 225 Pa的压力,在管道的下方施加10 000 Pa的支持力;最后,在模型的整体施加重力加速度载荷9.8 m/s2[13]。
1.5 地震波的输入
通过Peer Nga Strong Motion Database Record(佩尔·雅强震数据库记录)网站获取真实的地震波,所选的地震波都是低烈度小振幅震级比较低的地震波,地震波选用的都是SRSS多向地震动。在地震发生时会产生两个方向的地震波分量。其中,一个是沿水平方向的地震波分量,水平地震波分量是引起结构破坏的最主要因素;另一个是垂直方向的地震波分量,垂直地震波分量对埋地管道的破坏较小。
本文主要考虑地震波的均方误差(MSE)、地震波的强度(Arias Intensity)和地震波的最低可用频率(Lowest Useable Freq)。地震波的强度能够表示地震强度的大小,与地震动能量相关,是描述板块与板块之间相互挤压碰撞总强度的参量,可以准确地显示因板块的运动所引起的滑坡、砂土液化、结构破坏等情况。Arias Intensity值的计算公式为:
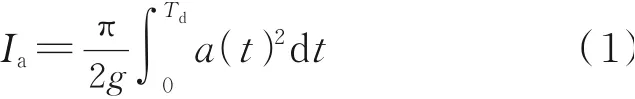
式中,a(t)为加速度,m/s2;Td为震动时间,s;g为重力 加 速 度,m/s2;Ia为 地 震 波的 强 度,m/s;t为 时间,s。
经过查阅大量垂直地震波分量相关的文献可知,垂直地震波对建筑物结构造成的破坏比较小,垂直地震波的加速度峰值约为水平地震波的1/3,因此很多学者都选择忽视垂直地震波的影响,故本文主要考虑水平地震波作为主要的观察方向[14]。选取几个阿里亚斯烈度(Arias Intensity)比较大的地震波,这些地震都发生在美国,并且地震的烈度都比较小。各地震波的信息见表3。表中,MSE值为地震波加速度的均方误差。

表3 各地震波的信息
北卡里夫地震波、尼加拉瓜地震波、圣费尔南多地震波的地震波均在5.00 s之后趋于稳定。为了使计算更加方便,北卡里夫地震波、尼加拉瓜地震波、圣费尔南多地震波都选用0~5.50 s进行计算,每0.01 s记录一个数值,而洛杉矶好莱坞地震波在10.00 s之后趋于稳定,所以洛杉矶好莱坞地震选用0~10.00 s进行计算。阿里亚斯烈度比较大的地震波如图4所示。
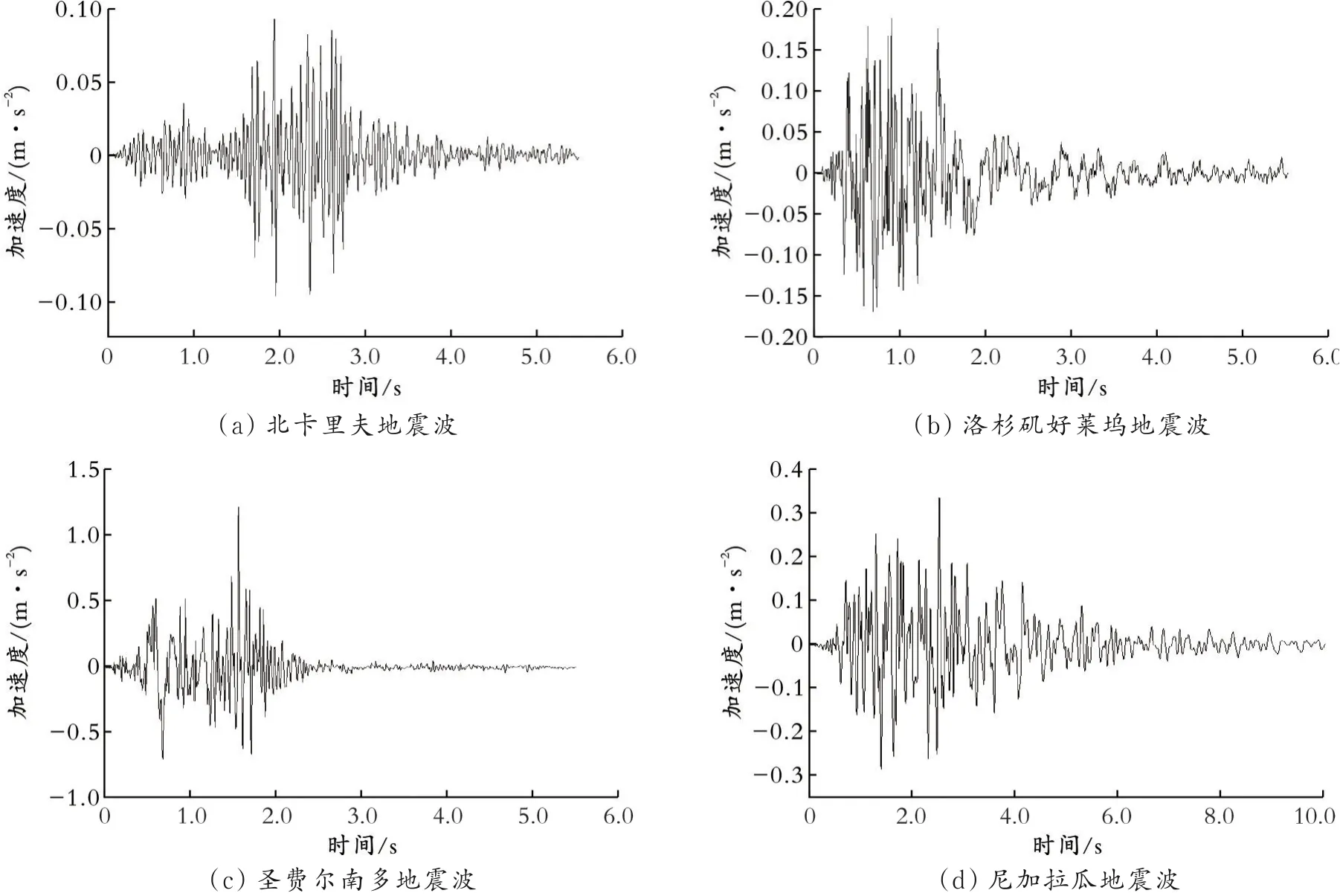
图4 阿里亚斯烈度比较大的地震波
2 结果分析
2.1 未施加地震载荷
管道的von Mises应力云图如图5所示,管道X方向的位移云图如图6所示。
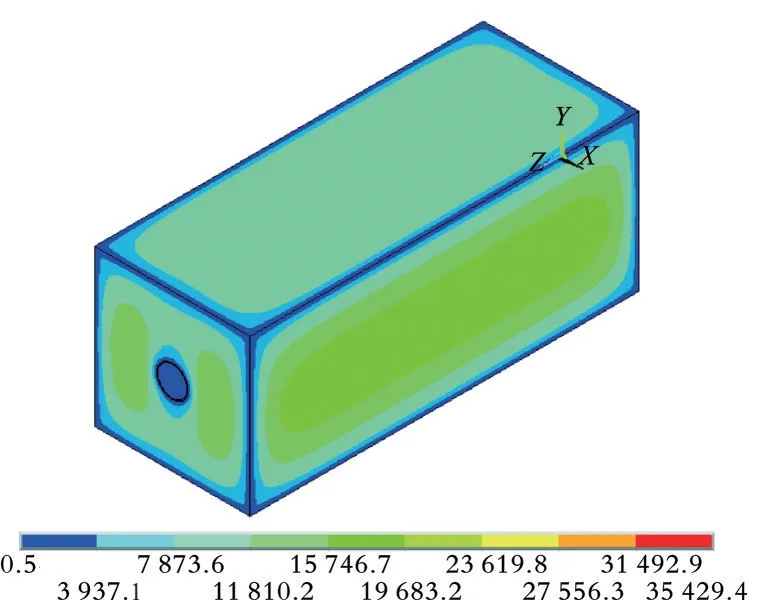
图5 管道的von Mises应力云图

图6 管道在X方向的位移云图
由图5可以看出,在未施加地震波时,土体所受的应力较小,管道周围受到的应力较大,最大von Mises应力为540 212 Pa。由图6可以看出,土体的位移均呈对称分布,发生在管道的两侧,最大位移为0.237 mm。
2.2 地震载荷作用下管道的动态响应
发生地震时,地震纵波对管道的影响很小,因此忽略地震纵波对埋地管道的影响,只研究地震横波对管道的影响。地震横波对管道轴向位移的影响较小,并且管道处于半无限空间中,沿管道X方向是无限的空间,故不研究地震横波对管道轴向位移的影响,只研究地震横波对管道垂直于轴向并平行于地面方向的位移,研究结果皆为管道垂直于轴向并平行于地面方向的位移。为了研究管道上不同点产生的位移,在管道上取不同点,研究管道上点1、2、3、4、5处的位移与时间的关系并进行对比,管道上不同点的分布如图7所示,北卡里夫地震波作用下管道上不同点的位移与时间的关系如图8所示。因为地震波是在X方向施加的,所以主要考察管道在X方向的位移随时间的变化。由图8可以看出,管道点5处产生了最大位移,最大位移为0.512 mm;管道点2处的位移也较大,其最大位移为0.511 mm,与管道点5处的最大位移相近;管道点1处的最大位移比管道点2处及管道点5处的最大位移小,其最大位移为0.414 mm,但比管道点3、4处的最大位移大;管道点3、4处的最大位移较小。换言之,在地震发生时,管道变形最大的位置为管道的上部和下部,管道两侧的位移相对较小。
图7 管道上不同点的分布情况
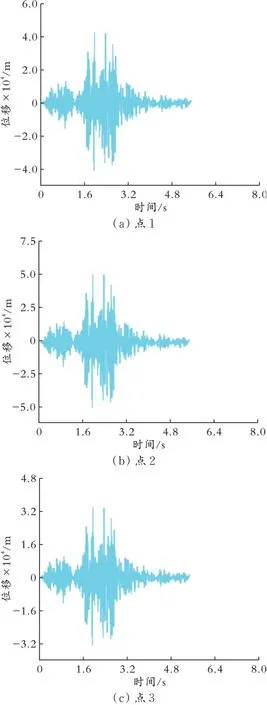
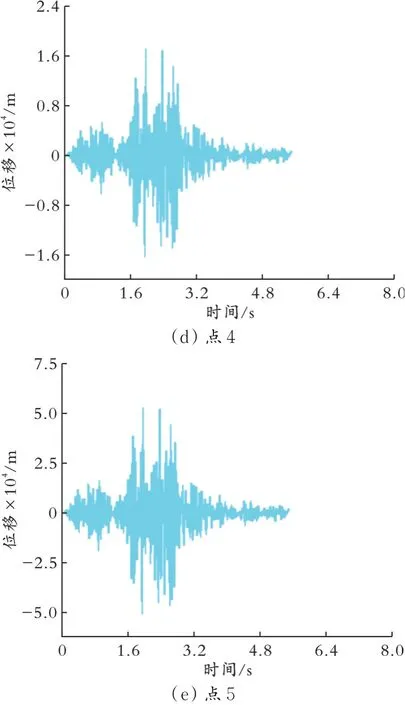
图8 北卡里夫地震波作用下管道上不同点的位移与时间的关系
2.3 不同地震波的结果比较
通过一组地震波施加的实验所得结论不具有准确性,因此若要验证此结论的正确性,则还需要进行大量的模拟实验进行对比。在此,继续对管道施加尼加拉瓜地震波、圣费尔南多地震波、洛杉矶好莱坞地震波,考察管道上不同点的位移,结果如图9所示。
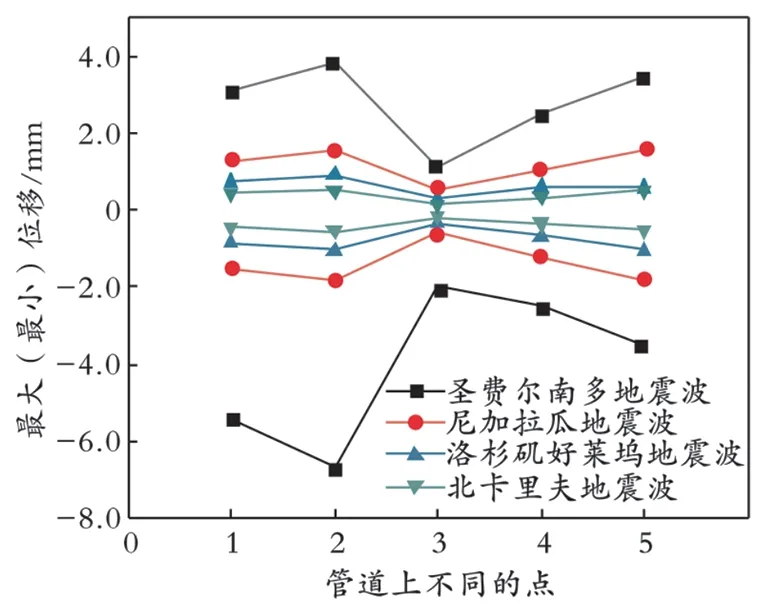
图9 施加不同地震波时管道上5个点的最大位移及最小位移
由图9可以看出,管道上部和下部所受的地震波的影响较大;不同的地震波施加在管道上时,均是在管道点2及点5处的位移较大,也就是管道点2及点5处的变形较大;管道点1处的位移小于管道点2及点5处的位移,但比管道点3和点4处的位移大;在4组地震波中施加圣费尔南多地震波时位移最大。
3 结 论
基于非线性理论,利用ANSYS有限元软件,建立了管道与土体的有限元模型;对模型进行网格划分,创建了管道与土体之间的接触模型;通过载荷的施加求解,得到了管道的von Mises应力云图和位移云图;讨论了施加不同地震波时对管道位移的影响。结果表明,管道的上部和下部在地震波的影响下产生了比较大的位移,地震时管道的上部和下部更容易遭到破坏;在地震波逐渐加大时,管道下部的位移减小,但仍然大于管道两侧的位移。研究结果对埋地管道破坏的预防以及管道工程中的修复加固具有一定的参考价值。
