鲁棒优化在电力系统机组组合中的应用综述
2022-05-19宫成宋靓云王卫王腾飞夏世威张东英
宫成, 宋靓云, 王卫, 王腾飞, 夏世威*, 张东英
(1.国网北京市电力公司, 北京 100031; 2.华北电力大学电气与电子工程学院, 北京 102206)
以新能源为主体的新型电力系统是传统电力系统的跨越升级,将促进风电光伏等新能源的快速增长。由于风电、光伏出力本身具有波动性和间歇性,风光等新电源高比例并网后将为电力系统运行带来较强的随机性,传统确定型优化调度方法较难适应新型电力系统的随机平衡需求,亟需建立适用于不确定条件下的优化调度运行方法[1-3]。而应用于日前调度的机组组合问题属于优化调度的关键环节,重新审视并探究随机环境下的机组组合问题,对增强电网的新能源消纳能力、提升电网不确定条件下的安全经济运行水平具有重要意义。
目前,针对不确定性条件下的机组组合问题研究方法主要包括随机优化[4-6](stochastic optimization,SO)和鲁棒优化(robust optimization,RO)[7-9]。随机优化方法依据历史数据概率分布情况生成大量离散样本,将不确定性优化问题的求解转化为多个场景集下确定性优化问题求解,但SO法存在以下缺陷:①随着场景集数目增加,其计算量急剧增加;②实际情况下随机变量的精确概率分布统计信息往往难以获取,使得SO法的可靠性大幅下降。而RO法以边界信息表征不确定变量的随机性,在最劣场景下制定相应决策以保证不确定集下的求解结果均为可行解。与SO法相比,RO法对不确定参数的具体概率分布函数形式不做要求,求解最优解的计算量也明显下降[10],因此被广泛应用于电力系统不确定优化问题的求解中。RO优化理论分为经典鲁棒优化方法和分布鲁棒优化方法。经典鲁棒优化方法最早由Soyster[11]提出,而后Ben-Tal等[12-15]和EI等[16-17]进一步发展了线性鲁棒优化以及仿射法和分解法等策略,使得经典鲁棒优化方法日渐完善与丰富。随着现代社会对更高精度的要求,进一步提出分布鲁棒优化方法以克服经典鲁棒优化求解的保守性,其核心思想是假定不确定性变量满足分布扰动偏差下的分布带。首先对经典鲁棒优化的不确定性集刻画、单阶段和两阶段鲁棒优化一般模型的构造,以及二阶段经典鲁棒优化机组组合模型及求解方法进行归纳。其次,对分布鲁棒优化的模糊集构建、分布鲁棒优化的机组组合模型及求解方法进行梳理。最后对鲁棒优化机组组合问题研究方向进行总结和展望。
1 经典鲁棒优化理论
1.1 不确定性集的构造
鲁棒优化本质为最劣情景下寻找最优解的过程,而不确定性集表征了随机参数的边界信息,因此不确定性集的构造极大影响了结果的保守性和准确性。常见的不确定性集包括盒式不确定性集、椭球不确定性集、基数不确定性集和N-K不确定性集(N为不确定向量的维数;K为保守性阈值常数)。
(1)盒式不确定性集:
U={ξ|eTξ=0,ξmin≤ξ≤ξmax}
(1)
式(1)中:e为单位向量;ξ为随机向量;ξmin、ξmax为不确定性变量变化范围上下界值。
盒式不确定性集以变量分布的临界信息为约束,保守性相对较高[18]。
(2)椭球不确定性集:椭球不确定性集可表示为[19]
(2)
线性约束下,当鲁棒优化模型的不确定性集为椭球集时,模型的求解工作可转为二阶锥问题,并可进一步转化为半定规划问题[20-22]。
(3)基数不确定性集:基数类不确定性集对不确定性参数的偏移量大小加以控制,数学模型为
(3)
通过调整不确定性度Γ的取值,能很好地表征随机变量的波动状况。
(4)N-K准则不确定性集:上述3种不确定性集均描述连续变量的分布情况,而N-K准则不确定性集适用于离散、非凸集合,可表示为
(4)
式(4)中:K值大小决定了不确定性集的保守性。
1.2 经典鲁棒优化模型
经典鲁棒优化模型包括单阶段鲁棒优化和两阶段鲁棒优化。
(1)单阶段鲁棒优化:其要求在不确定参数值确定之前制定决策。当不确定参数完成取值后,所做的决策需满足约束条件的限制。不失一般性,单阶段鲁棒优化模型概括为
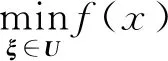
(5)
s.t.g(x,ξ)≤0
(6)
式中:x为决策变量;g(x,ξ)为约束条件集。
(2)两阶段鲁棒优化:与单阶段鲁棒优化相比,两阶段鲁棒优化中决策变量的一部分参数先于不确定变量确定,称为第一阶段决策变量,另一部分变量在第一阶段决策信息与不确定参数完成取值后确定,称为第二阶段决策变量,又称补偿变量。两阶段鲁棒优化一般模型可表示为[23-25]
(7)
s.t.h(x)≤0
(8)
g(y;x,ξ)≤0
(9)
式中:f1和f2分别为第一、第二阶段目标函数值;x为第一阶段决策变量;h(x)为相应的第一阶段约束;y为第二阶段决策变量,其值在第一阶段决策变量与不确定性变量都已给定后确定;g(y;x,ξ)为第二阶段约束集表达式。
2 经典鲁棒优化在机组组合问题中的应用
以含风电的两阶段鲁棒优化机组组合问题为例,从模型的构建和求解分别进行阐述。
2.1 经典鲁棒优化机组组合的两阶段模型构建
考虑风电不确定性的电力系统机组组合问题由两阶段鲁棒优化模型表示时:第一阶段为日前机组组合问题(unit commitment, UC),一般选择机组启停机状态等二进制变量作为决策变量,其不受场景集变化影响;第二阶段目标函数为最劣场景下优化系统运行成本期望值,当实际风机出力和第一阶段决策变量都已确定后,第二阶段决策变量包括对各机组出力进行灵活调节。两阶段鲁棒优化的电力系统UC模型可表示为
(10)
s.t.Ax≤d,x∈{0,1}
(11)
Bx+Cy+D(ξ)≤0
(12)
式中:c、b为常数向量;A、B、C为常数矩阵;x为第一阶段二进制决策变量,如机组的运行状态、启动状态、停机状态等;y为第二阶段决策变量,如机组出力、切负荷、切风电机组出力等物理量;D(ξ)为D(ξ)为不确定变量ξ的函数向量,受不确定性变量ξ影响。
2.1.1 模型的第一阶段构建
第一阶段不仅考虑机组启停成本,还包括第二阶段目标成本值,以常规机组开停状态、最小开停机持续时间为约束,其中机组状态为二进制变量。
(1)目标函数:
(13)
(2)约束条件:
(14)
(15)

t-1},∀g∈G,∀t∈1,2,…,T-2
(16)
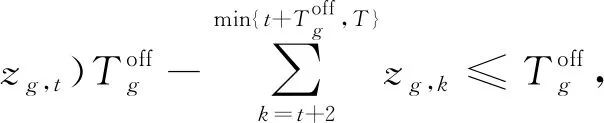
∀g∈G,∀t∈1,2,…,T-2
(17)
(18)
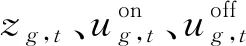
2.1.2 模型的第二阶段构建
第二阶段目标函数为最坏情景下经济调度成本、弃风成本及切负荷成本之和,约束集仅考虑机组输出功率上下限约束、功率平衡约束、爬坡约束、切负荷量约束和弃风量约束。
(1)目标函数:
(19)
(2)约束条件:
(20)
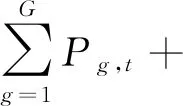
(21)
(22)
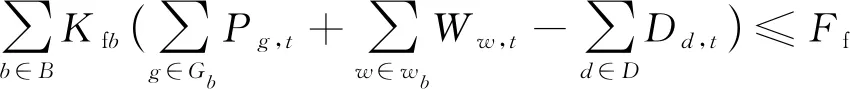
(23)
zg,tPg,min≤Pg,t≤zg,tPg,max
(24)
0≤Ww,t≤Ww
(25)

围绕上述理论,文献[26]对风电场、常规机组和热电联产机组综合模型下的调度问题进行了研究,其考虑的约束条件除常见约束集外,还计及系统热电联产机组中的电热耦合约束影响,更切合综合系统的实际运行情况。文献[27] 在基数不确定性集和多面体不确定性集约束下,求解了添加联络线容量约束、机组爬坡速率约束后的优化问题,并讨论上述约束及不确定性集对机组组合决策的影响。文献[28]考虑传输线安全容量限制约束、机组爬坡速率约束与不确定性集对调度决策影响,指出通过调整不确定性集参数值,系统旋转备用需求可自行满足。文献[29] 采用极端场景的不确定性集合描述可再生能源发电功率的变化范围,建立了考虑高比例可再生能源的机组组合鲁棒优化模型。针对该“min-max-min”3层优化问题,首先将原问题转换为混合整数线性规划问题,然后采用列约束生成(column and constraints generation,C&CG)算法进行求解,取得了较好效果。
2.2 经典鲁棒优化机组组合的两阶段模型求解
考虑不确定性因素的鲁棒优化问题为非确定多项式时间 (non-deterministic polynomial-time,NP)难问题,其在机组组合两阶段模型中的求解方法可分为两类:一是采用近似算法,假定第二阶段决策变量可近似表述为不确定性参数的线性函数,从而将两阶段鲁棒优化问题转为单阶段鲁棒优化问题;二是将鲁棒问题分解为主问题和子问题,主问题确定第一阶段决策变量,而子问题确定补偿变量及不确定性变量,并为主问题返回割集来更新约束。主从问题交替迭代求解,上下界趋同直至满足基于精度的收敛条件。
(1)近似算法。仿射策略法在近似算法中使用最为普遍,其假定第二阶段的决策变量即补偿变量y′与不确定性变量hun间呈线性函数关系为
y′=y0+Ghun
(26)
式(26)中:y0为hun=0时对应的决策变量值;G为参数值。
利用式(26)线性决策规则,建立决策变量与随机变量间的函数关系,从而将两阶段鲁棒优化问题转为单阶段鲁棒优化问题进行求解。文献[30] 在盒式不确定性集下,将第二阶段机组出力建模为不确定参数的线性仿射函数,从而将机组组合问题转化为单阶段优化问题,并利用对偶理论进一步将模型等价转化为标准混合整数规划问题(mixed integer linear programming,MIP),再通过商业求解器直接求解。文献[31]利用椭球不确定性集表述风速不确定性,基于仿射策略将原问题模型转化为二阶锥规划问题(second order cone programming,SOCP)问题,仿真表明所提方法合理,机组运行计划具有安全性与经济性。但采用仿射策略简化模型,决策灵活性降低,解也不再具有全局最优性[32]。为避免仿射法的局限性,文献[33]提出了分段仿射策略(piecewise affine polices, PAP),并将其与基本仿射策略法进行了比较,表明PAP法在各类不确定性集下均具有很好的应用性能。基于仿射策略,有采用二进制决策规则[34]、自适应求解法[35]、线性近似[36]对经典鲁棒优化模型的求解进行改进。
(2)分解算法。Benders分解法[37-39]和C&CG法[40]均将鲁棒优化模型分解为主问题(master problem,MP)和子问题(sub-problem,SP),交替迭代求解直至满足收敛条件。两者的区别主要在于,迭代过程中C&CG算法采用动态方式生成不确定集下决策变量的约束,在求解子问题时自动识别最劣场景集,随后将变量约束条件与场景集约束共同加入主问题约束条件中;而Benders方法基于子问题的对偶解生成变量约束,需对所有场景集的可行性进行判断,求解时间明显增加[41]。相比较于Benders分解法,分析和仿真表明C&CG分解法的迭代次数明显下降、收敛速度更快[42-44]。
但C&CG分解法也存在以下缺陷:由于模型的子问题为max-min结构的双层问题,需引入对偶理论将子问题的内层min问题转为max问题,从而与外层问题相结合,最终形成一个max下的单层优化问题以便求解,但此时转化模型出现了双线性项(二进制变量与连续变量相乘项),导致模型非凸不易求解。针对此问题,学者们提出了外近似法(outer approximation,OA)[45]和大M法[46]用以解决非凸性的问题。为解决OA法易陷入局部最优,文献[47]提出了改进OA法以保证全局最优。针对大M法求解时间过长、计算误差大的缺陷,文献[48]采用免对偶化的处理方法,利用模型第二阶段各场景集的相互独立性,将其转化为Ns(Ns为场景集数目)个并行SOCP问题,再通过商业求解器求解,极大提高了计算效率。
3 分布鲁棒优化理论
经典鲁棒优化法研究了最劣场景下的优化解,而最劣场景发生概率极低,因此经典鲁棒优化法的结果较保守。考虑到历史数据中的概率分布信息未得到充分利用,有研究将随机优化和经典鲁棒优化结合,提出了分布鲁棒优化方法(distributionally robust optimization, DRO)。DRO使用的随机变量分布集合不仅表征了边界情况,并综合了历史数据下的概率分布信息[49-51],为电力系统机组组合问题提供了新思路。
3.1 模糊集的构造
分布鲁棒优化模糊集的定义类似于经典鲁棒优化不确定性集,主要区别是:经典鲁棒优化不确定性集仅包含了随机变量的边界信息,而分布鲁棒优化模糊集全面综合了随机变量的边界信息以及概率分布信息,可表示为[52]
(27)
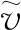
模糊集的保守性决定了分布鲁棒优化解的质量,满意的模糊集应满足特征[53]:①模糊集应最大程度包含随机变量所有可能出现的分布情况;②模糊集应足够小以避免病态数据的出现,从而确保决策不会过于保守;③模糊集应易于从数据中提取概率信息以确定分布集合中的参数取值,且在理想情况下,应有助于将分布式鲁棒优化问题转化为易处理、可利用成熟优化软件求解的数学表达式。
模糊集的构造方法主要基于以下两类策略。
(1)基于随机向量矩信息。基于一二阶矩信息构建的模糊集可表示为[54]
(28)
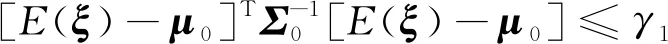
(2)基于随机变量概率分布信息。概率分布信息下的模糊集表征了实际概率分布P到额定分布P0的距离不超过扰动偏差值η,其中P0由经验推导所得。典型构造方法有Prohorov测度法[55]、散度函数法[56]、Wasserstein度量法[57-58]等。基于Kullback-Leibler散度函数构造的模糊集表示为[59]
(29)
DKL为P~P0的KL散度,可定义为
(30)
3.2 分布鲁棒优化模型
分布鲁棒优化的通用模型为
(31)
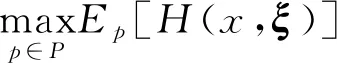
4 分布鲁棒优化机组组合模型及求解方法
4.1 分布鲁棒优化机组组合模型
分布鲁棒优化电力系统机组组合问题的一般形式为
(32)
式(32)中:Q为第二阶段目标函数值。
s.t.Ax≤b,x∈{0,1}
(33)
Bx+Cy+D(ξ)≤0
(34)
分布鲁棒优化下电力系统机组组合的目标函数、约束条件与经典鲁棒优化类似,均以总成本为目标值,以最大出力、旋转备用等作为约束。两种方法的主要区别在于对不确定性变量的描述及对应求解方法,即经典鲁棒优化以极限边界对不确定性变量加以叙述,而分布鲁棒利用历史数据的概率信息及边界来刻画不确定性变量[60-61]。基于分布鲁棒优化的电力系统机组组合问题求解过程如下。
4.2 分布鲁棒优化机组组合模型的求解
分布鲁棒优化模型转换与模糊集的形式密切相关,依据模糊集的不同,分布鲁棒优化机组组合问题的求解可分为以下两类。
4.2.1 随机向量矩模糊集下的分布鲁棒优化UC求解
当模糊集利用一、二阶矩信息构造时,可利用对偶和凸优化理论,将不确定性NP难问题转为确定性凸优化可解问题。文献[62]基于矩信息下的分布集,建立电力环保经济调度的分布鲁棒优化模型,并通过拉格朗日对偶定理、S-lemma理论和Schur补集,将原模型等价为确定性的半定规划问题求解。文献[63]提出了计及风电功率矩不确定性的分布鲁棒实时调度方法,将原有模型转为二次规划问题,进一步利用重构线性化技术将其转化为线性规划问题求解。文献[64-65]基于矩信息的模糊集构建了鲁棒机会约束模型,利用对偶理论和S-lemma消去随机变量,并通过Schur补集得到双线性矩阵(bilinear matrix inequality, BMI),最后利用循序凸优化算法(sequential convex optimization algorithm,SCOA)处理BMI中双线性项以完成风电场参与的分布鲁棒优化调度模型的求解。基于矩信息的分布鲁棒优化模型,其转换后的等价模型求解难度下降,但计算复杂度和计算量仍然较大,因此如何获得简单易算的等价模型需要进一步研究[66-67]。
4.2.2 随机变量概率分布模糊集下的分布鲁棒优化UC求解
相较于矩信息下的模糊集,以概率分布信息为核心构建的模糊集考虑了随机变量的概率分布特征,因此其对不确定性变量预估更佳。近似法和分解法仍适用于随机变量概率分布模糊集下的分布鲁棒优化UC问题求解工作。文献[68]结合统计推断技术、Devroye-Wise核估计和边界信息建立了模糊集;且随着历史数据增加,模糊集越接近真实分布信息,最终采用仿射策略将模型简化为易求解的混合整数线性规划(mixed integer liner programming,MILP)问题。文献[69]基于调度系统的历史数据,采用范数约束建立随机变量的概率分布模糊集,并利用Benders分解法寻找模型的全局最优解,仿真表明随着历史数据的增加,优化结果的保守性下降,当数据增加至无穷时,保守性消失。文献[26]综合考虑1-范数和∞-范数的影响,并利用C&CG算法替代Benders分解法对模型求解,增强了算法的收敛性。文献[57]提出了计及弃风成本与切负荷成本的数据驱动下的分布鲁棒储备和调度模型,采用数据驱动技术构建随机变量的Wasserstein球集,与基于矩信息构建模糊集的方法相比,前者包含更丰富的概率信息,且可通过改变Wasserstein球集的置信水平调整保守性,因此该模型可有效平衡系统优化结果的经济性与保守性。

表1 RO-UC和DRO-UC模型的对比Table 1 Comparison of RO-UC and DRO-UC models
综上所述,基于经典鲁棒优化的UC模型(RO-UC)以及基于分布鲁棒优化的UC模型(DRO-UC)各具特点,表1从RO-UC和DRO-UC的不确定性集刻画,模型优缺点、计算效率以及适用场景进行了详细对比和分析。
5 展望
分析和归纳分布鲁棒优化机组组合(distrbution robust optimization unit commitment,DRO-UC)问题所面临的挑战和机遇,以及未来研究重点和难点进行分析,具体如下。
(1)基于数据驱动的不确定性表征技术。DRO-UC模型考虑了不确定参数概率分布的不确定性以及边界信息,目前主要基于历史数据简单统计得到不确定参数的特征信息(如一二矩信息、参考概率分布等)。现有DRO方法虽然涉及统计信息不确定性的研究,但不确定性模型的构建和转化过程一般较为复杂。在智能方法、大数据技术快速发展的背景下,如何利用数据驱动技术分析历史数据,辅助表征统计信息的不确定性,并简化DRO 模型的转化求解过程是未来工作重点;且实际电力系统运行状态具有时间上的时序性和耦合性,现有DRO-UC模型主要表征了单一时间断面的不确定性集,而对于多时间断面对应的不确信集合相关性和耦合性缺乏研究,导致DRO-UC模型优化结果误差较大。如何利用数据驱动新技术方法处理DRO-UC模型的不确信集合时序相关性和耦合性,是未来研究工作的难点和重点。
(2)考虑高阶不确定性的分布鲁棒优化UC建模。构建以新能源为主体的新型电力系统,驱动了高比例风光新能源并网并带来电源侧的强随机性,同时多元化的产消者负荷如电动汽车、智能楼宇等具有电能消费及生产的双重属性,亦为负荷侧引入了一定的随机性。上述电源和负荷侧的多变量随机性,叠加上电网拓扑结构故障的不确定性,形成了高维不确定变量影响下的电力系统鲁棒优化调度问题,研究面向高阶不确定性的DRO-UC模型及高效求解方法是未来的工作重点,也是难点所在[70]。
(3)分布鲁棒优化UC模型高效求解方法。在考虑高维不确定性因素的DRO-UC问题中,并非所有不确定性因素都会对系统运行造成显著影响。如何分析辨识影响系统运行的关键不确定性因素,以保留关键不确定性因素、减少随机优化问题中随机变量的个数,降低分布鲁棒优化UC问题的求解难度,从而提高优化问题求解效率是未来工作的重点和难点。同时为提高DRO-UC的可解性,往往将原模型转为等价SDP模型,但求解计算量随着系统规模增大呈指数级增加,如何有效控制等价模型的求解难度和计算量,并保证模型的优化结果的精度是亟待解决的又一难点问题。
6 结论
(1)机组组合问题是电力系统调度运行的基础问题之一。随着新型电力系统的建设,风光等新能源大规模并网以及负荷侧产销者负荷涌现,电力系统系统调度运行面临不确定因素增多,对机组组合建模及求解提出了新的挑战,而鲁棒优化理论为解决上述问题带来了新的途径。
(2)对基于鲁棒优化理论的电力系统机组组合研究进行综述。经典鲁棒优化对随机变量概率分布特征不作要求,在计算速度上优于随机优化法,但其求解工作在最劣场景下开展,故基于经典鲁棒优化的鲁棒优化机组组合(robust optimization unit commitment,RO-UC)模型优化结果保守性高、经济性差。相对于RO-UC模型,DRO-UC模型考虑了不确定变量概率分布的不确定性,兼具了随机优化方法的经济性和RO方法的鲁棒性,DRO-UC模型在新型电力系统调度运行中将具有广泛应用,对未来新型电力系统适应复杂不确定性因素具有重要价值。
