基于改进粒子群算法的梯级水风光短期调峰优化调度
2022-05-19张艳华黄静梅黄景光邓逸天李振兴
张艳华, 黄静梅, 黄景光*, 邓逸天, 李振兴
(1.三峡大学电气与新能源学院, 宜昌 443002; 2.国网重庆电力公司永川供电分公司, 重庆 402160)
随着可再生能源发电的建设规模增大,其发电并网的容量占比大幅提升。但可再生能源发电,尤其是光伏和风力发电的不确定性,加剧了电力系统调峰调频的困难,给快速跟踪调节电源响应的能力带来了严峻挑战[1-2]。且在价格因素的推动下,可再生能源投产后会与其他能源抢占负荷空间和输出通道,同时导致产生弃风、弃光的现象,反而对提高可再生能源的消纳能力无实质性的作用[3-4]。水电机组可以快速启动停运,且可调的发电容量范围大,能够迅速对负荷变化做出反应,因此可作为优质的调峰电源用于电力系统调峰[5-6]。利用水电机组调峰能力来调节光伏电场和风电场的有功输出,实现水风光联合运行,可以显著提高光伏发电、风力发电的利用率,进一步探索清洁能源的发展模式,为未来清洁能源的发展起着重要的示范作用[7-9]。
针对负荷空间受限和输出通道矛盾导致的高弃风、高弃光率的问题,国内外的专家学者对此展开了大量研究,其解决办法包括:提高电网调节等效负荷的能力和电力网络的传输能力;提出风-水日间联合调峰策略,将水电作为调峰电源以达到削峰填谷的目的,使得联合系统出力更加平稳[10];利用梯级水电站的调蓄作用,将风电、光电接入水电以增加其可调度性[11];在保证电力系统安全稳定运行的条件下,使风光互补电力动态经济调度达到最优等方法[12]。针对上述所提的解决办法建立了不同的算法模型,其中包括:以平抑风光出力波动为目标建立风-光-水联合系统发电效益最大的模型,并提出依赖动态调整学习因子的免疫粒子群算法,使得建模更加准确,计算精度更高[13];以风光水系统总发电量最大为目标的优化调度模型,保证满足系统调度规则的前提下使系统发电效益达到最高[14]。
鉴此,以湖北一梯级水电站与附近的风光电场为研究对象,在风-光-水联合系统模型的基础上[13-14]建立了系统余留负荷均方差最小的梯级水-风-光电站联合调峰短期调度模型,并提出利用收缩因子和基于佳点集法的改进粒子群算法(particle swarm optimization,PSO)来改善建模和提高算法精度。研究梯级水风光互补联合调度运行方法,发现该方法可最大程度地消纳风电和光电,缓解电网调峰压力,减少了弃风、弃光现象,保证了系统调度运行的发电效益。
1 梯级水风光联合互补调度的必要性和可行性分析
截至2015年底,坐落于湖北宜昌的清江三级梯级水电站(简称梯级A),坐落于湖北恩施的利川汪营风电场(简称风电场B1)、天上坪风电场(简称风电场B2),装机容量分别为400 MW、300 MW,坐落于湖北武汉的花山光伏电场(简称光电场C),其装机容量为200 MW。梯级水电站A共分为3个梯级(A1、A2、A3),各级电站基本参数如表1所示。

表1 梯级各电站基本参数特征
风光电场由于供电片区负荷小,主变限制了其并网容量,造成年累计弃风电量约为9 470 MW。若将风光接入水电,利用水电的输出通道打包外送出去,势必会减少风电、光电的浪费。
研究梯级水-风-光联合调度,首先分析梯级A是否能对两个风电场B1、B2以及光电场C的出力进行补偿。分析梯级A对风电补偿的出力可以发现,A1梯级电站在5月和7月满足不了风电的最大补偿需求,但在剩余月份A1梯级电站均可完全补偿[15];以能够充分满足风电补偿需求为前提,发现将A1、A2梯级电站联合运行后,其剩余的补偿出力也可满足光电所需。其次从互补容量分析,风-光电站总装机容量为900 MW,占梯级电站A总装机容量(3 052 MW)的32.15%。最后从互补电量进行分析,梯级A电站的年平均发电总量约为8.48×109kW·h,风-光电场的年平均发电总量约为9.03×108kW·h,占梯级A的10.65%,联合互补输出可使输出通道增输10.65%的电量。
根据上述分析可知,从出力补偿能力、互补容量及互补电量这3个方面上都可为研究梯级A与周围风电场和光电场互补联合调度提供理论支撑和基础。
2 梯级水风光联合调峰短期调度数学模型
以系统余留负荷均方差最小为目标函数,并以水电站不影响下游来水需求和基本用水要求为目标,建立一个日内调峰模型。所提调度策略为先对风电、光电进行补偿,要求互补部分为风电和光电的装机容量之和(900 MW),再利用水电自身剩余可调出力安排调峰。
2.1 目标函数
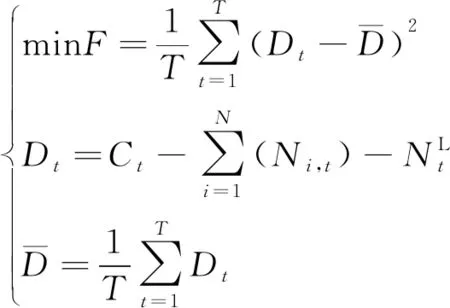
(1)
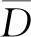
2.2 约束条件
(1)水量平衡约束:
Vi,t+1=Vi,t+(Ri,t-Qi,t-qi,t)Tt
(2)
式(2)中:Vi,t+1和Vi,t分别为第i个梯级电站在t+1和t时段时的水库库容,m3;Ri,t为第i个梯级电站在t时段区间的入库流量,m3/s;Qi,t为第i个梯级电站在t时段的发电流量,m3/s;qi,t为第i个梯级电站在t时段的弃水流量,m3/s;Tt为调度期内第t时段的时长,h。
(2)水量联系约束:
Ri,t=Qi-1,t-Δti-1+qi-1,t-Δti-1+Ii,t
(3)
式(3)中:Δti-1为第i-1~i个梯级电站的水流滞时对应的时段;Ii,t为第i-1~i个梯级电站的区间平均入库流量,m3/s。
(3)发电流量约束:
Qi,min≤Qi,t≤Qi,max
(4)
式(4)中:Qi,t为第i个梯级电站在第t时段的发电流量,m3/s;Qi,min、Qi,max分别为第i个梯级电站在第t时段允许发电流量的最小值和最大值,m3/s。
(4)库容约束:
Vi,min≤Vi,t≤Vi,max
(5)
式(5)中:Vi,t为第i个梯级电站在第t时段的库容量,m3;Vi,min、Vi,max分别为第i个梯级电站死水位所对应的最小库容和正常蓄水时所对应的最大库容(汛期则为防洪水位所对应的防洪库容),m3。
(5)出力约束:
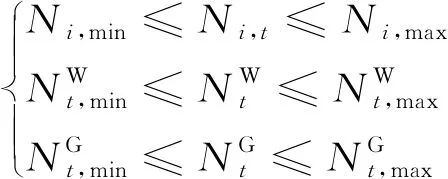
(6)
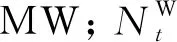
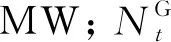
分别为光电场在第t时段允许出力的最小值和最大值,MW。
(6)出力补偿约束:
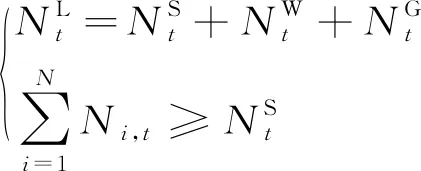
(7)
其他约束条件包括梯级电站水库的库容约束、水头限制约束、梯级电站发电的引水流量约束及各变量值不为负等。
3 基于改进PSO算法的模型求解
3.1 PSO算法的改进
3.1.1 种群的初始生成
初始种群的分布与整个算法的寻优过程有着密切的联系,PSO算法的初始种群都是随机生成的,导致有的生成点可能聚集在一个区域,使得粒子相似度较高且容易局限搜索空间,影响算法的计算时间和速度,同时解的质量不高。为提高解的质量,希望生成点均匀分布在区域的各个角落,因此提出了佳点集法。佳点集法是一种均匀取点的方法,可将初始种群均匀分布在搜索空间中,与一般粒子群随机初始化种群有着明显区别,提高了初始种群的多样性[16-17]。现在[-10,10]的二维区间内将20个点用随机生成法和佳点集法实现,结果对比如图1所示。
3.1.2 引入收缩因子λ
PSO算法的权重系数w值的大小会对算法求解的结果产生很大影响,其取值通常采用线性递减的方式。计算前期w较大,全局搜索能力强,虽然保证了种群的多样性下,但仍希望加强局部搜索能力,能快速高效地找到最优解;计算后期w较小,粒子无法大范围搜索,使得过早陷入局部最优,不能满足种群的多样性,导致得到的最优解不可靠。
vi(t+1)=wvi(t)+c1rand1(pbest-xi)+
c2rand2(gbest-xi)
(8)
xi(t+1)=xi(t)+vi(t+1)
(9)
w线性递减并不是对所有问题都是有效的,因此引入收缩因子λ确保算法收敛,其计算公式为
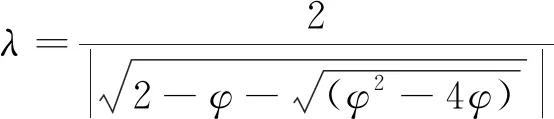
(10)
式(10)中:中间替代变量φ=c1+c2,φ>4。
vi(t+1)=λ[vi(t)+c1rand1(pbest-xi)+
c2rand2(gbest-xi)]
(11)
3.2 改进PSO算法应用于短期调峰优化调度流程
应用于短期调峰的改进PSO算法流程如图2所示。按要求输入计算所需参数,并根据上述约束条件通过不断调整粒子适应度值计算梯级各电站出力,直至满足迭代终止条件后输出最终所需计算结果。
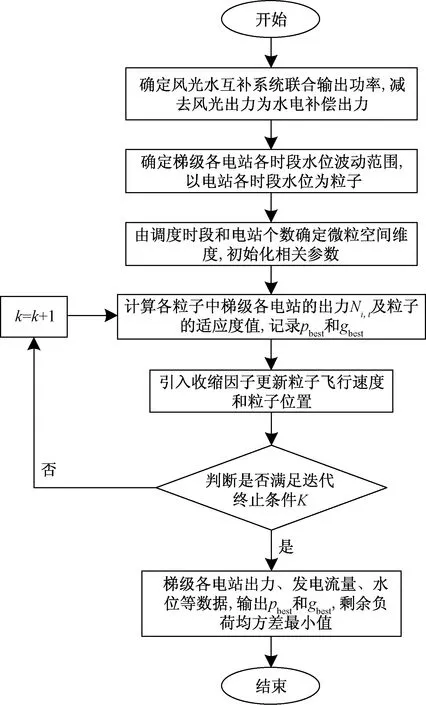
K为迭代终止条件;k为迭代次数图2 改进PSO算法流程Fig.2 Improved PSO algorithm flow
4 算例仿真分析
鉴借已建成的龙羊峡水-光互补电站的模型[18],并以梯级A,风电场B1、B2和光电场C作为研究对象。选取丰水期典型日(2014年8月15日)、平水期典型日(2014年11月15日)和枯水期典型日(2014年1月15日)3个时间的风电、光电场实时出力以及梯级水电站的入库流量作为模型的仿真输入,梯级各电站水位为决策变量,A1、A2、A3电站的起调水位分别为381.21、378.56、375.05 m。
以一天24 h为调度周期,调度时段为1 h,从0:00开始到24:00结束,共可划分为24个调度时段。利用改进的PSO算法对模型进行求解,其参数设置为c1=c2=2.03,迭代次数500,种群规模50。为简化计算过程,将两个风电场出力合为一个风电场出力。在纯梯级电站调峰(纯梯级)和梯级水-风-光电站联合调峰(联合系统)方案下建立系统余留负荷均方差最小的联合调峰短期调度模型。
4.1 算例结果对比
4.1.1 丰水期典型日
由图3所示,在纯梯级A参与电网负荷调峰后,在17:00时系统的负荷达到峰值,在凌晨4:00系统负荷值达到最小,峰谷差减小为7 461.17 MW,降幅12.05%;在风光水互补的梯级水电站调峰后,系统最大峰值出现在20:00与最小谷值出现的时刻同纯梯级调峰一致,但系统峰谷差为7 383.77 MW,较原始负荷减少了12.96%。丰水期典型日调峰后的负荷剩余曲线较为平缓,但在9:00—11:00调峰后负荷变化趋势同原负荷,没有发挥明显削峰作用。
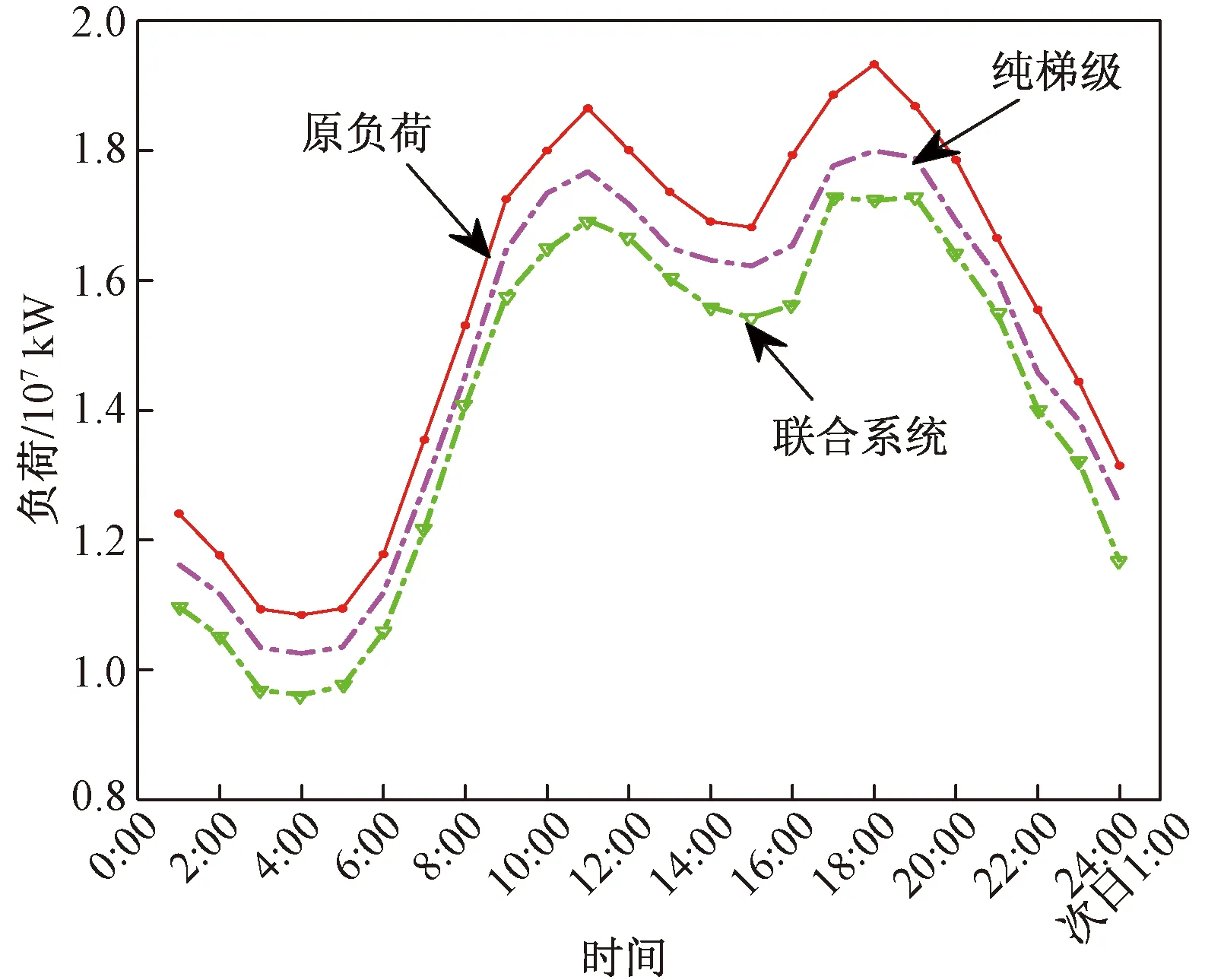
图3 丰水期典型日系统负荷图Fig.3 Typical daily system load diagram during wet season
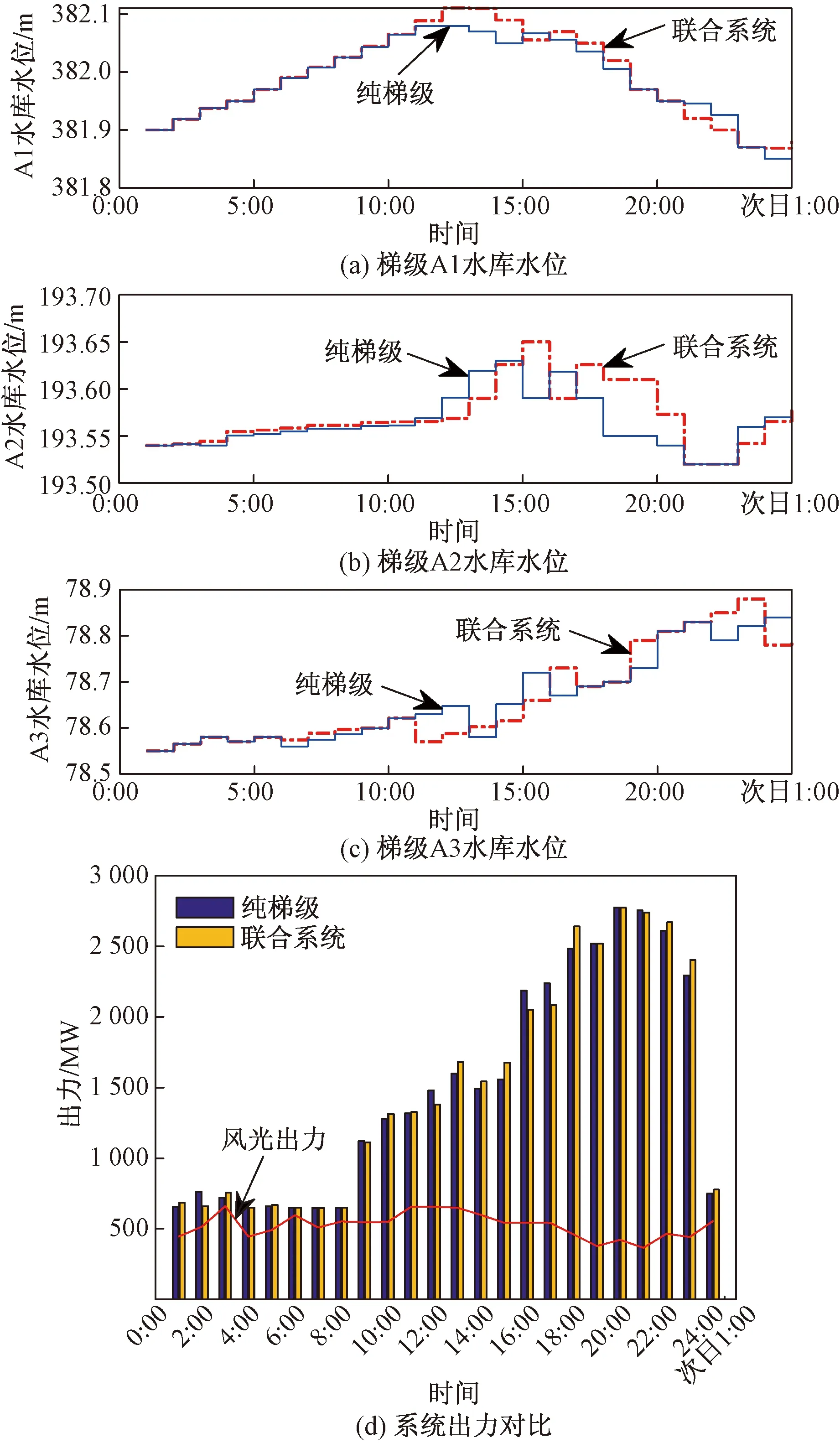
图4 丰水期典型日下系统水位变化过程以及出力对比Fig.4 Variation process of water level and comparison of system output under typical days in wet season
如图4(a)~图4(c)所示,纯梯级调峰下A1电站在0:00—10:00,发电流量小于入库径流,几乎可按保证出力使得水位逐渐调高至382.22 m;8:00开始逐渐加大出力,下泄流量增大,电站水位略微下降后再提升保持高水头发电;18:00至调度期末水位降到381.94 m;A2电站的水位与上游A1电站的下泄流量有很大联系,库容较A1小,11:00后A2水位随A1下泄流量的增大而稳步提升;A3为日调节电站,在19:00—21:00时段,来自A2大量下泄流量使得其水位涨幅剧烈。
根据图4(d)可得,在梯级水-风-光电站联合调峰下,因为风电、光电作为调峰容量的一部分,在用电的低谷时期24:00—次日6:00和14:00—18:00时段梯级电站出力较小,因此水位较纯梯级调峰高;19:00—22:00时段以增大发电流量的形式增加出力。A2在A1减小出力时,因上游电站下泄来水量减小,水位较纯梯级略低,但也呈稳步上升趋势。A3电站日内水位变化同纯梯级调峰,波动较大且呈上升趋势。
4.1.2 平水期典型日
在两种不同方案下,纯梯级调峰后余留负荷均方差为6.47×1012kW2;梯级水-风-光电站联合调峰调度下,系统余留负荷均方差为6.38×1012kW2。如图5所示,在纯梯级A参与电网负荷调峰后,在17:00时系统的负荷达到峰值,在凌晨4:00系统负荷值达到最小,峰谷差减小为7 461.17 MW,降幅12.05%。梯级水-风-光电站联合调峰后,系统最大峰值出现在20:00和最小谷值出现的时刻同纯梯级调峰一致,但系统峰谷差为7 383.77 MW,较原始负荷减少了12.96%。平水期典型日调峰后的负荷剩余曲线较为平缓,但在9:00—11:00调峰后负荷变化趋势同原负荷,没有发挥明显削峰作用。
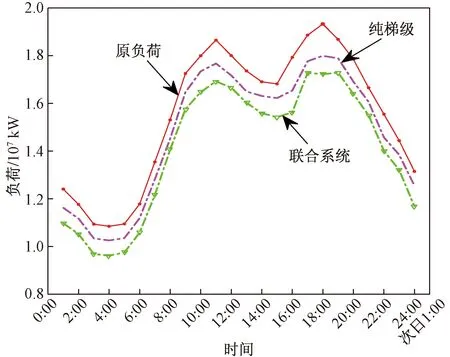
图5 平水期典型日系统负荷图Fig.5 Typical daily system load diagram during normal water period
如图6所示,平水期典型日下,两种调峰方案中的梯级总出力均表现为“双峰”型,深夜负荷用电低谷时段0:00—7:00,梯级各电站水位变化不明显,系统出力总和几乎不变。由于风光电供应一部分负荷,最终表现为8:00—12:00时段A1水位提升约0.05 m,18:00—21:00时段增加发电流量参与调峰。至调度期末,A1水位无变化,A2水位增加0.2 m,A3水位降低0.2 m,A1、A2水位波动较明显。
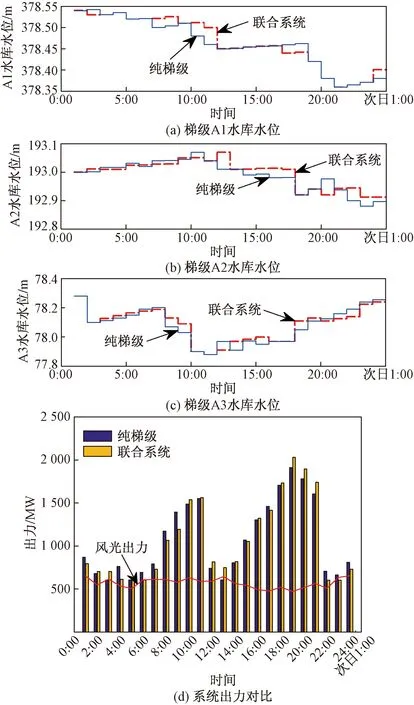
图6 平水期典型日下系统水位变化过程以及出力对比Fig.6 Variation process of water level and comparison of system output under typical days in normal water period
4.1.3 枯水期典型日

图7 枯水期典型日下系统负荷图Fig.7 Typical daily system load diagram during dry season
在两种不同方案下,纯梯级调峰后余留负荷均方差为7.34×1012kW2;梯级水-风-光电站联合调峰调度下,系统余留负荷均方差为7.22×1012kW2。如图7所示,纯梯级A参与电网负荷调峰后,在17:00时系统的负荷达到峰值,在凌晨4:00系统负荷值达到最小,峰谷差减小为7 801.30 MW,降幅8%。梯级水-风-光电站联合调峰后,系统最大峰值出现在20:00和最小谷值出现的时刻同纯梯级调峰一致,但系统峰谷差为7 732.07 MW,较原始负荷减少了8.9%。梯级水-风-光联合系统调峰曲线从直观上看更为平坦光滑。但由于枯水期少水,两种调度方案下发电量均没有丰、平水期多,因此调峰容量小,调峰效果比丰、平枯水期差。
两种调度方案下各电站水位变化与梯级出力对比如图8所示。枯水期典型日下,整个梯级入库来水径流小,调度初始的用电低谷时期同丰、平水期一致,风光的并网可使水电站少发的电量以水量的形式储存起来,待到用电高峰时再以较大发电水头发电,但由于A1库容大,蓄水量并未导致A1水位发生变化。随着发电流量增大,两种运行方案下水位均表现为逐渐降低,到调度末期的负荷低谷时水位才稍微有所上升,但方案2较方案1在17:00—20:00时段水位降低0.02~0.03 m。A2、A3库容较小,水位受A1下泄流量影响较大,整个调度期内水位波动较为明显。梯级发电量平均出力在900 MW左右,主要集中在负荷高峰时期出力。

图8 枯水期典型日下系统水位变化过程以及出力对比Fig.8 Variation process of water level and comparison of system output under typical days in dry season
两种方案下,在平水期、丰水期、枯水期三种典型日下调峰效果对比如表2所示。

表2 不同典型日下纯梯级与联合系统调峰对比
由表2可得,在3种不同典型来水日下梯级水-风-光电站联合调峰较纯梯级调峰,无论是对减小系统余留负荷方差还是削弱系统峰谷差方面都是有益的,为基荷电源出力创造更好的环境。其中余留负荷均方差平均再降0.14×1012kW2,峰谷差平均减少97.28 MW。此外,梯级水电站因补偿风光,时段内的出力大小会有所调整。同时风、光电看作“虚拟水电”与水电捆绑输出全额入网,也间接性地增加了系统的调峰容量。且在丰、平、枯水期典型日下联合系统中梯级水电站A日内出力分别增加202.15、148.16、15.42 MW。若考虑电价后,以目前湖北水电0.38元/kW·h的上网电价计算,可为梯级日均增加46 268.8元的收益。
4.2 验证改进粒子群算法的有效性
为验证改进PSO的优势及应用于梯级水电站调度的有效性,采用基本PSO求解丰水期典型日下纯梯级调峰,与改进后PSO作对比验证,结果如图9、表3所示。
可以看出在迭代初期,改进后的PSO在惯性因子的作用下比基本PSO收敛速度快。随着迭代次数的增加基本PSO在约第110次收敛于5.89×1012kW2,计算时长为14.27 s,陷入局部最优解;而改进后的PSO在为第240次收敛于5.80×1012kW2,优化结果优于PSO,计算时长为14.88 s。
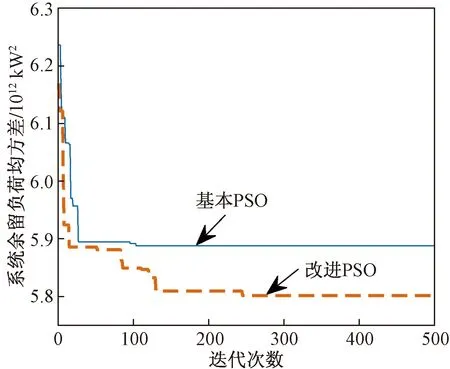
图9 算法对比结果Fig.9 Algorithm comparison results

表3 算法优化对比
这是由于种群初始化的均匀分布,扩大其寻优范围,避免了算法前期的趋同性,以牺牲计算效率获得更好的寻优效果。
5 结论
建立了系统余留负荷均方差最小的梯级水-风-光电站联合调峰短期调度模型,分析了联合调度的短期调峰能力和梯级短期调度运行产生的影响,为今后湖北能源集团梯级水、风电与光伏电站联合调峰发电提供参考价值。得出如下结论。
(1)通过与纯梯级调峰模式对比,风电、光电并入水电一起参与电网调峰调度,可使系统余留负荷均方差平均再降0.14×1012kW2,使得负荷曲线的峰谷差进一步缩小,增加了调峰容量,对改善火电频繁启停工作有着积极作用。
(2)风电、光电与水电互补后形成的联合上网系统,水电补偿风电、光电,保障风光电全额入网,避免弃风、弃光现象的产生。同时,不额外增加水电机组增设的投资费用但增加了水电发电量,丰、平、枯水期典型日下联合系统中梯级水电站A日内出力分别增加202.15、148.16、15.42 MW,提高了企业的经济效益。
(3)引入收缩因子后,改进PSO有更好的收敛速度;利用佳点集法使粒子初始种群均匀化,扩大了寻优范围,增强了种群的多样性,可以得到更优质的解。
若要讨论梯级水-风-光电站联合调峰调度对企业经济效益的影响,在后期还可将价格因素考虑其中构成多元化目标函数。同时,随着未来对调峰电源需求量的增加,今后工作中还可进一步将抽水蓄能电站加入调度模型。
