基于遗传算法神经网络的地源热泵夏季低负荷运行性能预测分析
2022-05-19董艳芳朱辉曾召田门玉葵梁秒梦
董艳芳, 朱辉*, 曾召田, 门玉葵, 梁秒梦
(1.桂林航天工业学院能源与建筑环境学院, 桂林 541004; 2.桂林理工大学土木与建筑工程学院, 桂林 541004; 3.广西建筑新能源与节能重点实验室, 桂林 541004)
工业、建筑和交通用能已成为中国CO2排放量占比最大的行业,而大量的CO2排放导致气候变暖的问题已经引起人们的广泛关注。国家大力提倡应用新能源代替或辅助化石能源,以提高可再生能源利用率和降低CO2排放量。地热能作为一种清洁、高效、环保的新能源,已在建筑空调系统中得到了广泛的推广和应用。
地源热泵系统运行能效直接影响着工程全寿命周期的经济效益,长期的运行性能监测不仅费时不经济,而且只能用于后评估,因此通过短期能效比测评预测地源热泵系统中长期能效比对评估地源热泵系统经济效益具有重要意义。近年来,预测模型有比例积分微分(proportion integration differentiation,PID)控制算法[1]、MLR(mixed logistic regression)算法[2]、MLR算法与层次分析法结合模型[3]、支持向量机[4]、回归预测模型[5]、人工神经网络(artificial neural network,ANN)算法[6]、反向传播神经网络(back propagation neural network,BPNN)[7]等,还有应用能耗模拟软件对地源热泵系统各部件模型[8]进行系统能耗及能效进行预测研究。实际地热工程应用主要是通过短期实测数据进行能效评估。Tang等[9]应用聚类算法建立HVAC系统模型模拟系统的短期运行性能预测;Wang等[10]利用短期测评数据总结了地源热泵项目应用效果。这些测试效果精度均比较高,但对短期测试时长或测试数据量及数据质量还是有一定要求。崔治国等[11]、于丹等[12]研究了空调系统能耗监测数据预处理方法及对能耗的影响;傅强等[13]基于短期实测数据采用回归模型对上海地埋管地源热泵系统夏季运行性能进行了分析。严磊等[14]、Yan等[15]对武汉地区多个地热能示范项目进行了能效测评,基于数据挖掘法对比6种预测模型(标准或穷尽的卡方自动交互检验、BPNN、径向基函数网络、分类回归树及支持向量机),得出了BPNN模型用于地源热泵系统能效比预测效果最优化,并分析了短期测评与长期运行性能的预测研究。
前人建立的地源热泵能效预测模型精确度较高,但因地热能应用能效与气候特点、地质条件、运行工况等因素相关,未必适用于系统低负荷率工况下的运行性能预测,也不一定适用于桂北地区气候条件和岩溶地质条件下地源热泵系统研究。考虑到BPNN预测模型中的连接权值及阈值是随机产生的,优化权值及阈值的选取可提高BPNN模型的预测性能。为此,在董艳芳等[16]对岩溶地区系统低负荷率工况下地源热泵能效比已计算的研究基础上,采用遗传算法优化的BPNN模型预测岩溶地区系统负荷率低于30%运行工况下地源热泵系统的能效比,并应用此模型研究夏季工况短期能效测评与中长期能效比评估的关系。
1 工程概况
研究工程为岩溶地质条件下桂林地区“一院两馆”地热应用示范项目,总建筑面积105 965 m2,其中大剧院面积9 500 m2,图书馆面积32 475 m2,博物馆面积34 195 m2。系统总冷负荷为9 980.3 kW,总热负荷为6 197.6 kW,生活热水负荷300 kW。夏季制冷工况冷冻水供/回水温度7 ℃/12 ℃,冬季制热工况热水供/回水温度50 ℃/45 ℃。
1.1 地源热泵空调热水系统
地埋管换热井数量总共852口井,井深100 m,竖井间距为5 m,根据建筑使用功能分区域设置于室外绿化带和道路下,辅助冷却塔调节冷热不平衡问题。在设计工况下,夏季运行27台热泵机组和10台余热回收型热泵机组+冷却塔辅助的空调热水系统;冬季运行15台热泵机组和5台余热回收型热泵机组空调热水系统;过渡季节运行5台余热回收型热泵机组,设置成热水优先模式的空调热水系统,地源热泵机组及循环水泵的设备参数如表1所示。地源热泵系统现阶段长期处于系统负荷率<30%工况下运行,采用用户侧回水温度控制热泵机组的启停,更好地适应建筑负荷的变化。
1.2 数据监测采集方法
地源热泵系统运行时间基本是工作日8:30—16:30,周末及法定节假日停机,特殊情况(大剧院表演节目安排在非工作时间段)地源热泵系统照常运行。为了详尽记录低负荷率工况条件下地源热泵系统运行情况,地源热泵系统选取夏季工况(6—8月)的现场运行数据,外接数据记录仪R7100实时记录水温、流量的变化。为避免开机阶段测试参数波动较大及保证测试数据的精度,采集9:00—16:00 用户侧及地源侧供回水温度、流量、室外气温、相对湿度和热泵机组负荷率机组开启台数等参数的逐时值及日累计耗电量,采集设备具体参数如表2所示。
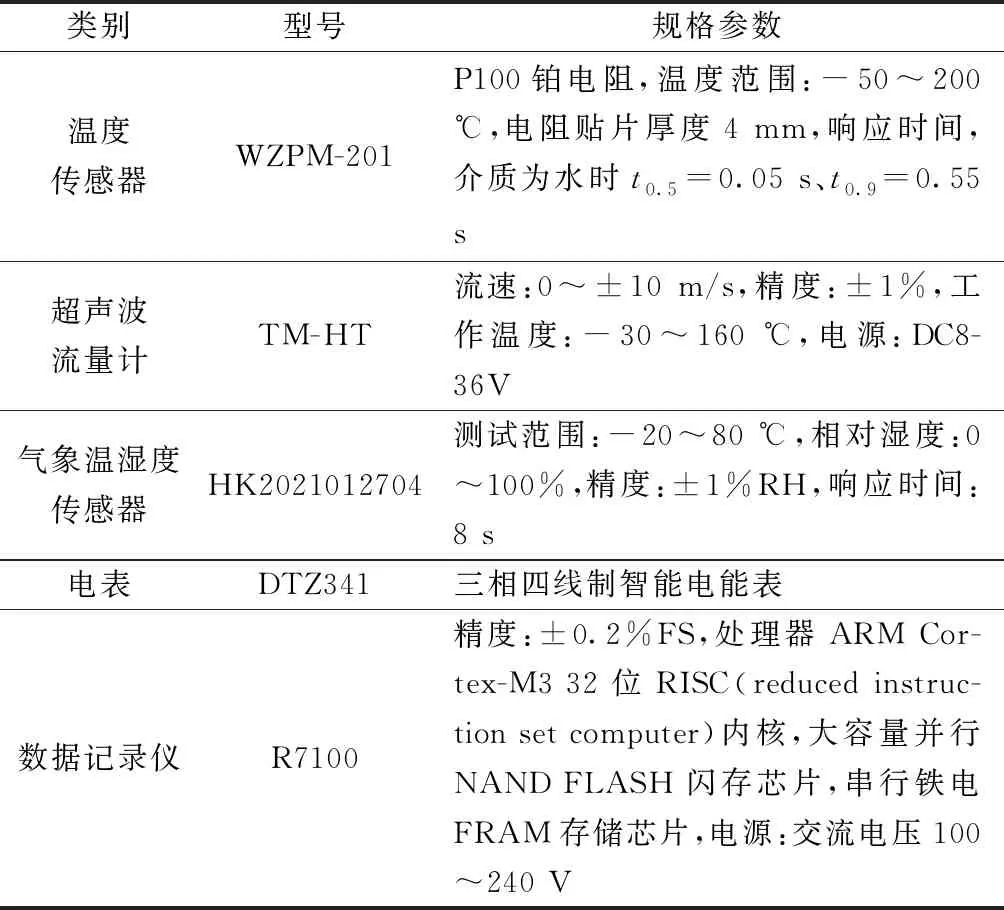
表2 测试仪和相关传感器参数
2 研究方法及模型建立
2.1 BPNN模型
BPNN模型是一种按误差逆向传播算法训练输入参数,学习某种规则,不断地修正神经元间连接的权值和阈值,以使得BPNN预测值与期望输出值的误差均方差为最小,已广泛应用于各领域的预测优化研究。BPNN由输入层、隐含层和输出层组成,每一层内有若干神经元,相邻层间的神经元通过权值w连接,各神经元内设阈值b。

图1 BPNN拓扑结构Fig.1 Topology structure of back propagation neural network
根据文献[17]对影响地源热泵系统制冷和制热工况下运行能效的特征参数重要度排序可知,制冷工况下特征参数重要度排序为:机组负荷率、地源侧回水温度、地源侧供水温度、用户侧回水温度、室外温度、用户侧供水温度、室外相对湿度,由此建立的网络拓扑结构如图1所示。输入层神经元为7个,输出层神经元为2个,选择合适的隐含层节点数,在很大程度上影响着BPNN的预测性能。隐含层神经元按照经验公式[式(1)、式(2)],不断地试验预测值与真实值间的误差以获得最优的隐含层神经元数量,并防止因隐含层节点数过多导致过拟合问题。
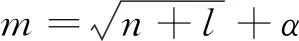
(1)
式(1)中:m为隐含层节点数;n为输入层节点数;l为输出层节点数;α为隐含层神经元节点的调节数,取值一般为[1,10]。
m=2n+1
(2)
假定输入节点特征参数为xj,输入层节点j和隐含层节点i间连接的权值为ωj,i,隐含层节点的阈值为bi,隐含层输出为xi,输出层节点k的权值为ωi,k,阈值为bk,输出层输出为yk。隐含层和输出层的输出计算公式为
xi=f(neti)
(3)
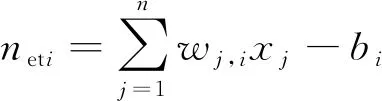
(4)
yk=f(netk)
(5)

(6)
式中:neti为神经网络输入层到隐含层的净输入;netk为神经网络隐含层到输出层的净输出;f为激活函数,在这里采用双曲正切函数tansig,其表达式为
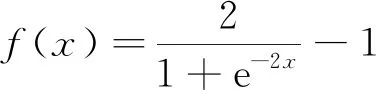
(7)
输入样本正向传递,输出值与期望值的误差反向传递,不断地调整及修正各层的权值w和阈值b,其误差函数E表达式为
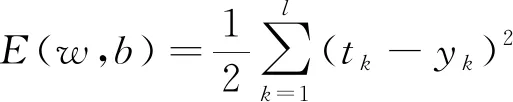
(8)
式(8)中:tk为输出层第k节点的期望值。
BPNN的权值和阈值一般是通过初始化为[-0.5,0.5]区间的随机数,初始化参数的选取对网络训练影响很大,由于权值和阈值的初始值无法准确获得,导致BPNN预测易陷入局部最优的可能性,因此引入遗传算法优化BPNN的初始权值和阈值。
2.2 基于遗传算法BP神经网络的优化预测模型(GA-BP)
遗传算法是模拟自然界遗传和生物进化论而成的一种并行随机搜索最优化方法。遗传算法是在引入优化参数形成的编码串联群体中,按照所选择的适应度函数并通过遗传中的选择、交叉和变异对个体进行筛选,保留适应度好的个体,淘汰适应度差的个体,新的群体既继承了上一代的信息,又优于上一代,反复循环,直至获得满足条件的最优解。
遗传算法用于优化BPNN预测模型的权值和阈值以提高地源热泵系统能效比的预测精度。遗传算法优化的BPNN计算流程如图2所示。种群初始化时,个体编码包含输入层和隐含层连接权值、隐含层阈值、隐含层与输出层连接权值以及输出层阈值。适应度计算函数是用个体初始权值和阈值训练好的BPNN预测输出能效比,将预测能效比与真实能效比的误差绝对值之和作为个体适应度值F,其计算公式为

图2 GA-BP算法计算流程Fig.2 GA-BP algorithm calculation process
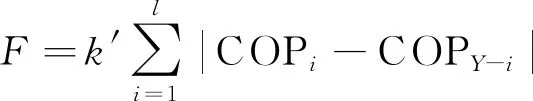
(9)
式(9)中:COPi为BPNN第i个节点的真实能效比;COPY-i为第i个节点的预测能效比;k′为系数。
计算流程中的选择操作采用基于适应度比例的选择策略,个体i被选中的概率为
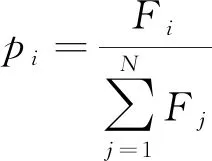
(10)
式(10)中:Fi为个体i的适应度值;N为种群个体数目。
交叉操作方法采用实数交叉法,第k个染色体ak和第l个染色体al在j位的交叉操作方法为
akj=aij(1-brandom)+aljbrandom
(11)
式(11)中:brandom为[0,1]区间的随机数。
alj=alj(1-brandom)+akjbrandom
(12)
变异操作从种群中随机选取保留下来的个体,以一定变异概率改变某些基因产生更优秀的个体,第i个个体的第j个基因aij进行变异操作的方法为
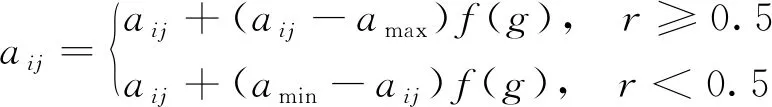
(13)
式(13)中:amax和amin分别为基因aij的上界和下界;g为当前迭代次数;r为[0,1]区间的随机数;f(g)的表达式为
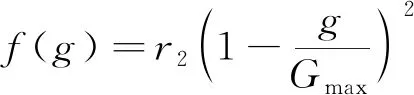
(14)
式(14)中:r2为随机数;Gmax为最大进化次数。
基于遗传算法的BPNN预测模型对网络初始权值和阈值进行实数编码成染色体后进行优化,可以从一个集合开始并行搜索最优权值和阈值,大幅降低陷入局部最优解的情况。
夏季工况总共采集了528组逐时数据,因地热系统处于极低负荷率工况下运行,监测到每日开启机组台数不变,逐时能效比变化不大,因此将采集数据整理成逐日数据(周末和节假日除外),总共66组,将42组数据用于训练网络,24数据组用于测试网络,逐时能效比预测选取典型日进行分析。
3 误差分析指标
选用平均绝对误差(mean absolute error,MAE)、绝对误差的标准差(standard deviation of absolute error,Std_AE)、平均绝对误差百分比(mean absolute percentage error,MAPE)、平均相对误差的标准差(standard deviation of absolute percentage error, Std_APE)进行模型精度评估,MAE、绝对误差的标准差Std_AE、MAPE和平均相对误差的标准差Std_APE反映了预测值和真实值之间偏离程度,数值越小表示模型预测精度越高,其数学表达式分别为

(15)
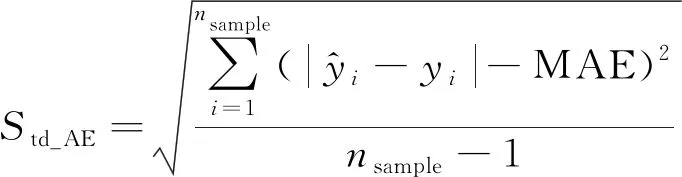
(16)
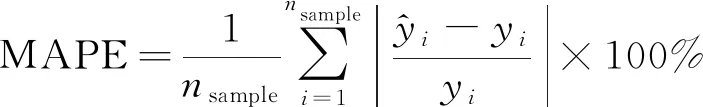
(17)
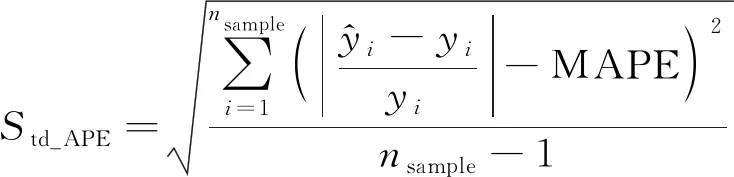
(18)
4 模型验证及预测误差分析
4.1 GA-BP预测模型验证及误差分析
本地热应用项目在低负荷率工况下运行时,仅运行地埋管换热系统,无需冷却塔作为辅助冷源,一般开启热泵机组3~7台。夏季运行工况下,影响系统能效比COPsys及机组能效比COP的重要特征参数实测值如图3所示。室外温度介于23~37 ℃,相对湿度介于40%~99%,整体而言6月温度比7、8月低,相对湿度比7、8月高,温度与相对湿度近似成镜像图,主要是因为6月初夏桂林雨水较多,而7月、8月从小暑逐渐步入处暑,气温较高,雨水稍少。地源侧供回水温度在27.5~34.65 ℃,地源侧平均供回水温差为2.81 ℃,用户侧供回水温度在7.16~15.56 ℃,用户侧平均供回水温差为2.4 ℃。热泵机组开启台数占比最大的是3~4台,热泵系统负荷率大多介于7.8%~10.3%,因热泵机组选型及台数配比合理,机组负荷率基本维持在50%~80%内。由于6月下旬和7月下旬—8月初室外温度较高,相对湿度稍低,建筑负荷较大,机组开启台数增加,土壤排热量随之增加,地源侧供回水温度升高,用户侧供回水温度也相应地升高,以保证机组负荷率达到额定值的60%及以上。
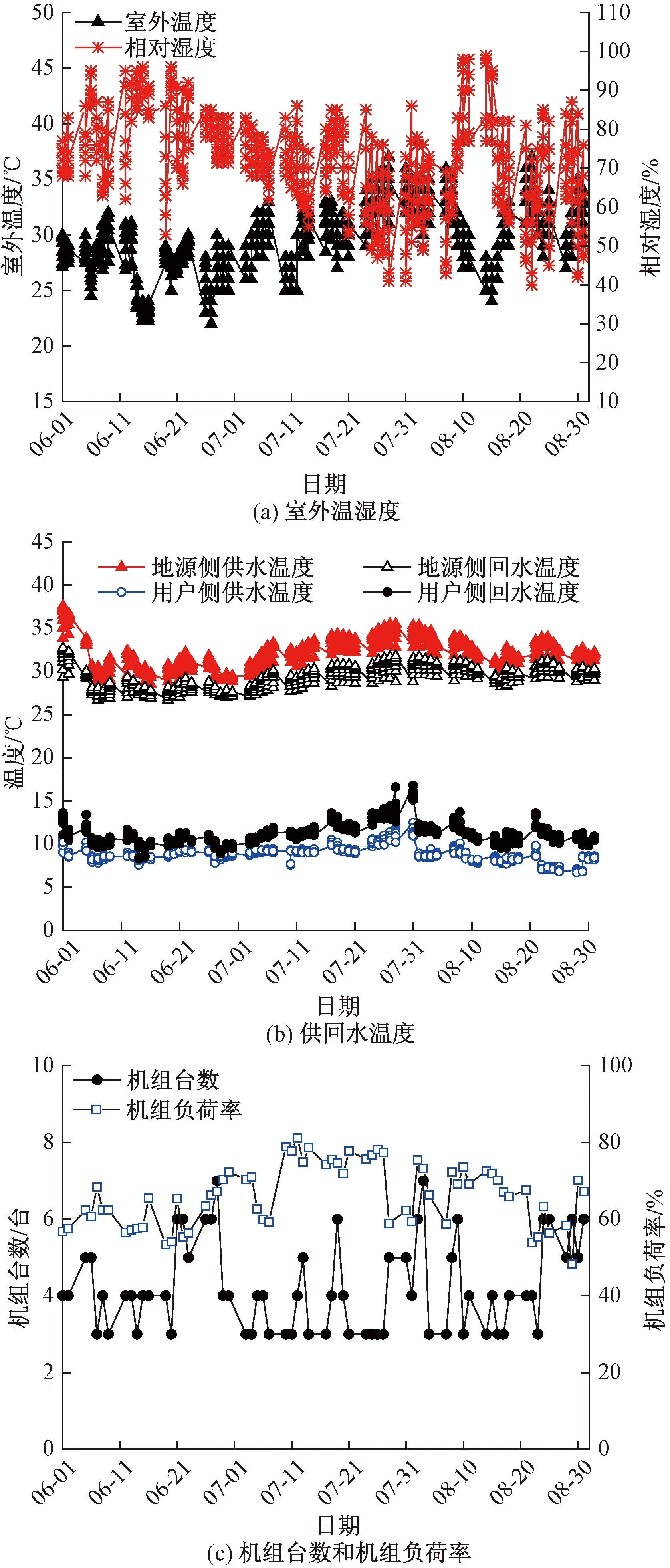
图3 热泵机组台数与模型输入参数Fig.3 Number of heat pump units and model input parameters
根据以上分析的气象因素及负荷特点,将按时间推移顺序采集的样本顺序打乱随机排序,以提高GA-BP神经网络预测模型的精确性。为了验证GA-BP神经网络预测模型的可靠性及精确性,分别采用文献[15]中最优模型BPNN和GA-BP神经网络模型预测桂林地区地源热泵系统的COPsys及COP,并将其预测值与COPsys及COP计算值进行对比分析,如图4所示。COPsys及COP的计算方法已在文献[16]中阐述过,这里将不再赘述。从图4可知,GA-BP神经网络预测的COPsys及COP与计算值基本一致,比BPNN预测值波动幅度较小,吻合度更好。

图4 两模型预测值与计算值对比Fig.4 Comparison of predicted value of two models and calculated value
由GA-BP和BPNN预测模型的能效比相对误差对比结果(图5)可知,BPNN预测的COPsys及COP相对误差介于±12%,波动幅度较大,GA-BP预测值的相对误差基本在±5%以内,波动幅度较小。BPNN与GA-BP预测模型的误差评价指标如表3所示。可以看出,GA-BP神经网络模型预测误差评价指标MAE、Std_AE、MAPE和Std_APE均比BPNN模型更小,具有更高的预测精度,更适合于桂林地区地源热泵应用工程能效比评估的预测。

图5 能效比预测值的相对误差分析Fig.5 Relative error analysis of predicted value of energy efficiency ratio
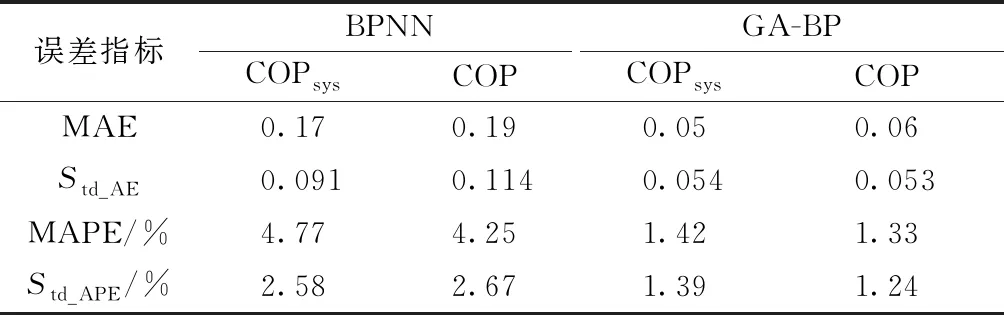
表3 GA-BP与BPNN预测模型误差分析
4.2 交叉率及变异率对适应度的影响
GA-BP神经网络预测精度更高的主要原因是:GA-BP采用遗传算法优化了BPNN预测模型的随机连接权值和阈值,对样本数据和测试数据的适应性更好。在遗传算法中,交叉率c和变异率mratio的选取在种群进化过程有着重要的作用,对算法的性能有重要影响。为了获得最优连接权值和阈值,选取进化代数为40,种群规模为20,分析不同交叉率和变异率对适应度值的影响,结果如图6所示。图6(a)给出的是变异率为0.1时,交叉率对适应度的影响,可以看到交叉率从0.6~0.9 适应度均能达到最佳适应度,其中交叉率为0.7时,达到最佳适应度最快,波动幅度也最小,这说明所获得最优连接权值和阈值的时间更短,预测精度更稳定可靠。图6(b)为交叉率为0.7时,不同变异率对适应度的影响。可以看出,变异率为0.005时,进化代数达到10之后,适应度值已达到最佳适应度,没有波动,这表明此取值下获得最优权值和阈值更快,预测误差更小,预测模型更为可靠。据上述分析结果,在本文模型中,交叉率和变异率分别取值为0.7和0.005。
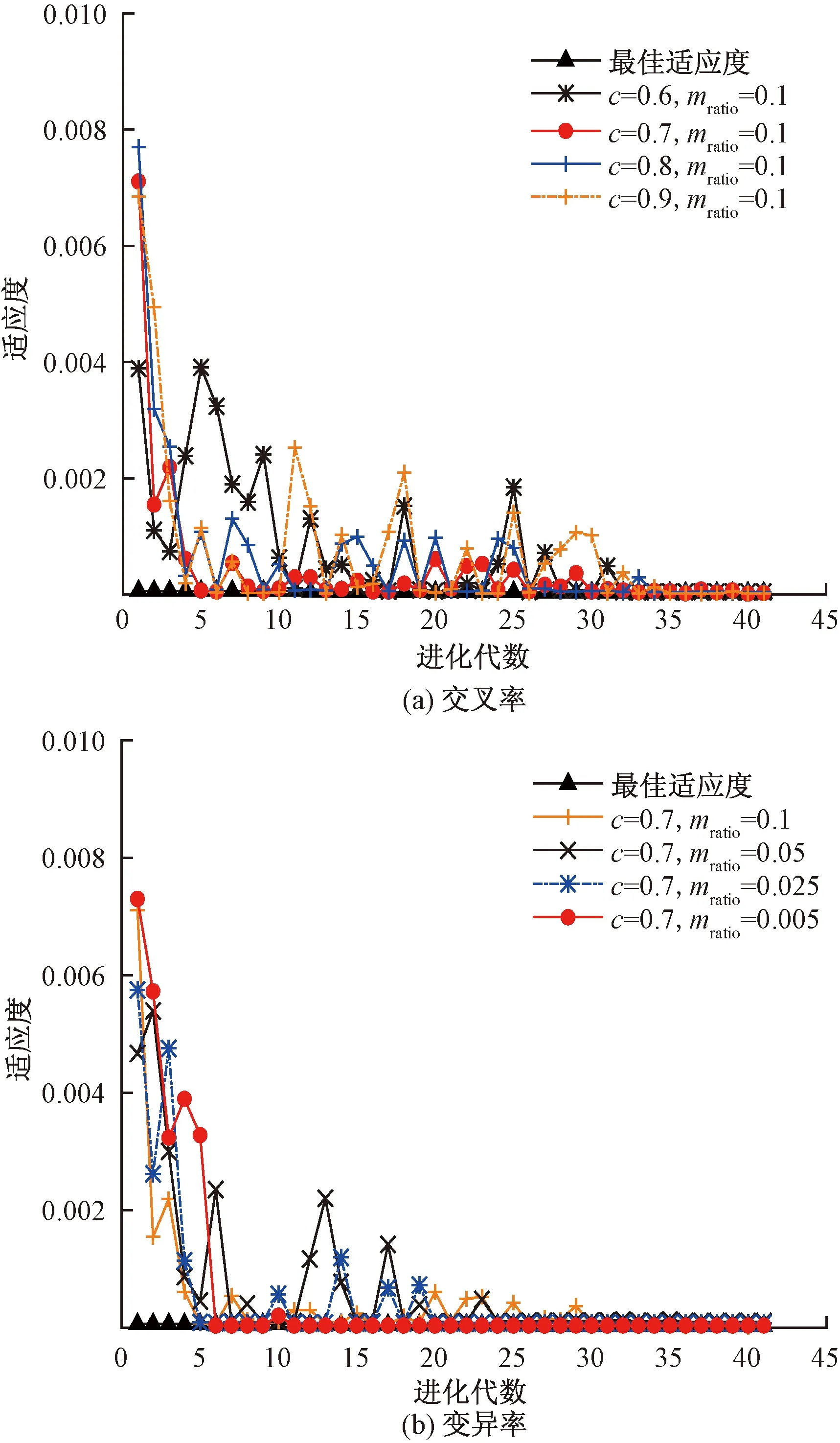
图6 交叉率及变异率对适应度的影响Fig.6 Effect of crossover rates and mutation rates on fitness
5 短期测评与中长期能效比分析
地源热泵系统前期运行在系统低负荷率工况下,每一年夏季变化天气特点相似,建筑开启空调区域相同,则COPsys及COP具有季节周期性,可以将夏季地源热泵系统实测的COPsys及COP平均值作为低负荷率工况下中长期夏季COPsys及COP预测值。实际工程中地热能应用能效评估,大多数通过监测短期数据用于中长期能效测评,选择监测天数越多越接近长期运行能效比。
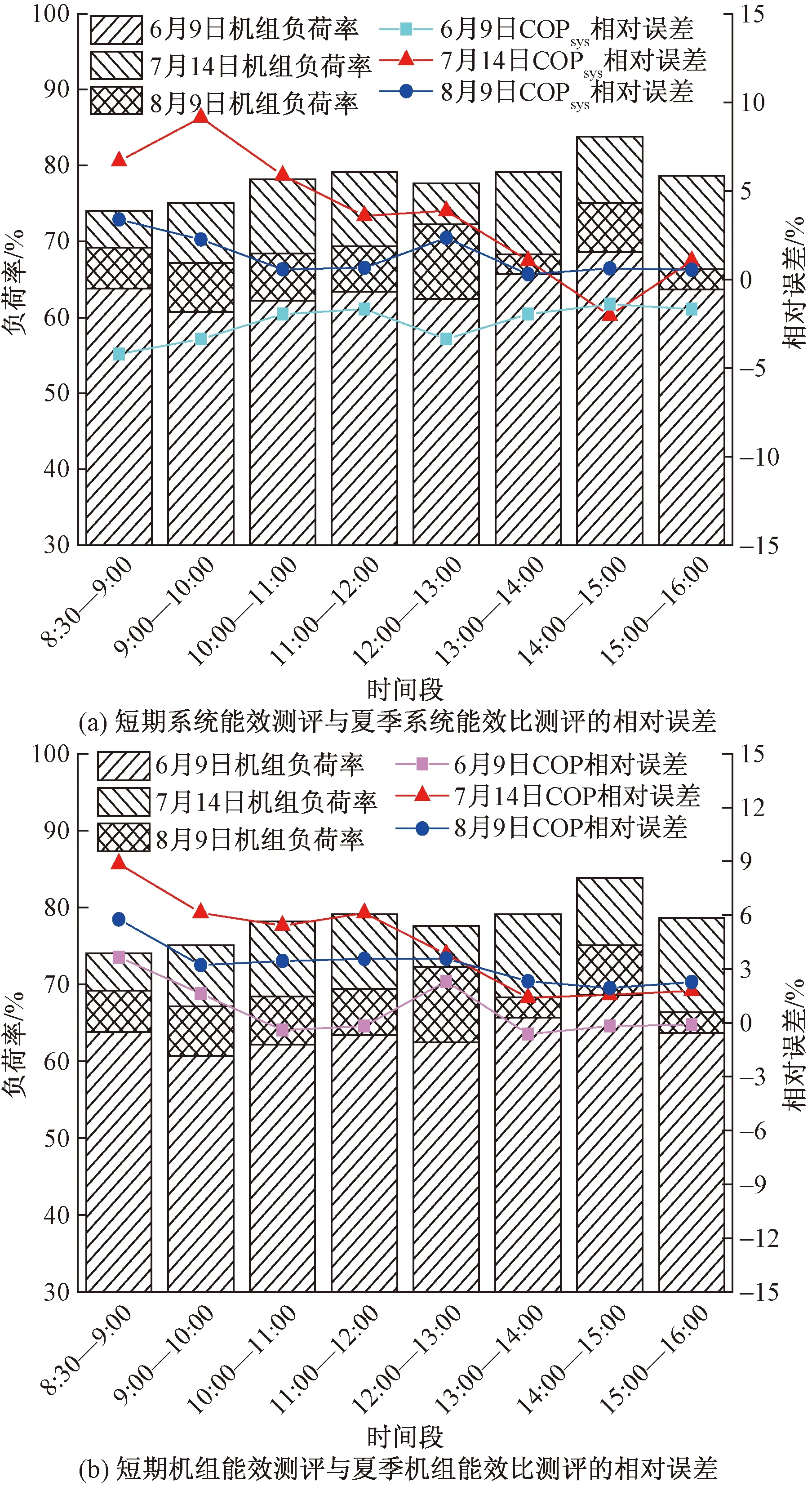
图7 一天短期测评能效比与夏季能效比的相对误差Fig.7 Relative error of energy efficiency ratio between short-term evaluation in a day and in summer
本项目采用1 d不同时刻和不同天数短期测试的能效比与整个夏季平均能效比进行对比分析,以确定合适的短期测试时段采用GA-BP神经网络模型预测评估地热能中长期运行能效。选取6月9日、7月14日、8月9日不同时刻的能效比与整个夏季能效比的误差分析如图7所示。6月9日、7月14日、8月9日不同时刻的系统能效比与整个夏季能效比的误差分析如图7(a)所示。可以看出,6月9日和8月9日10:00—12:00和14:00—16:00实测的COPsys的相对误差较小,7月14日14:00—16:00 COPsys的相对误差较小。短期机组能效测评与夏季机组能效比测评的相对误差如图7(b)所示。可以看出,6月9日、7月14日和8月9日10:00—12:00的COP稍大于14:00—16:00的COP相对误差;而COPsys及COP相对误差小的机组负荷率均为60%—80%。综合以上分析,保证机组负荷率处于60%以上,选择一天当中14:00—16:00作为短期测评COPsys及COP相对误差较小。
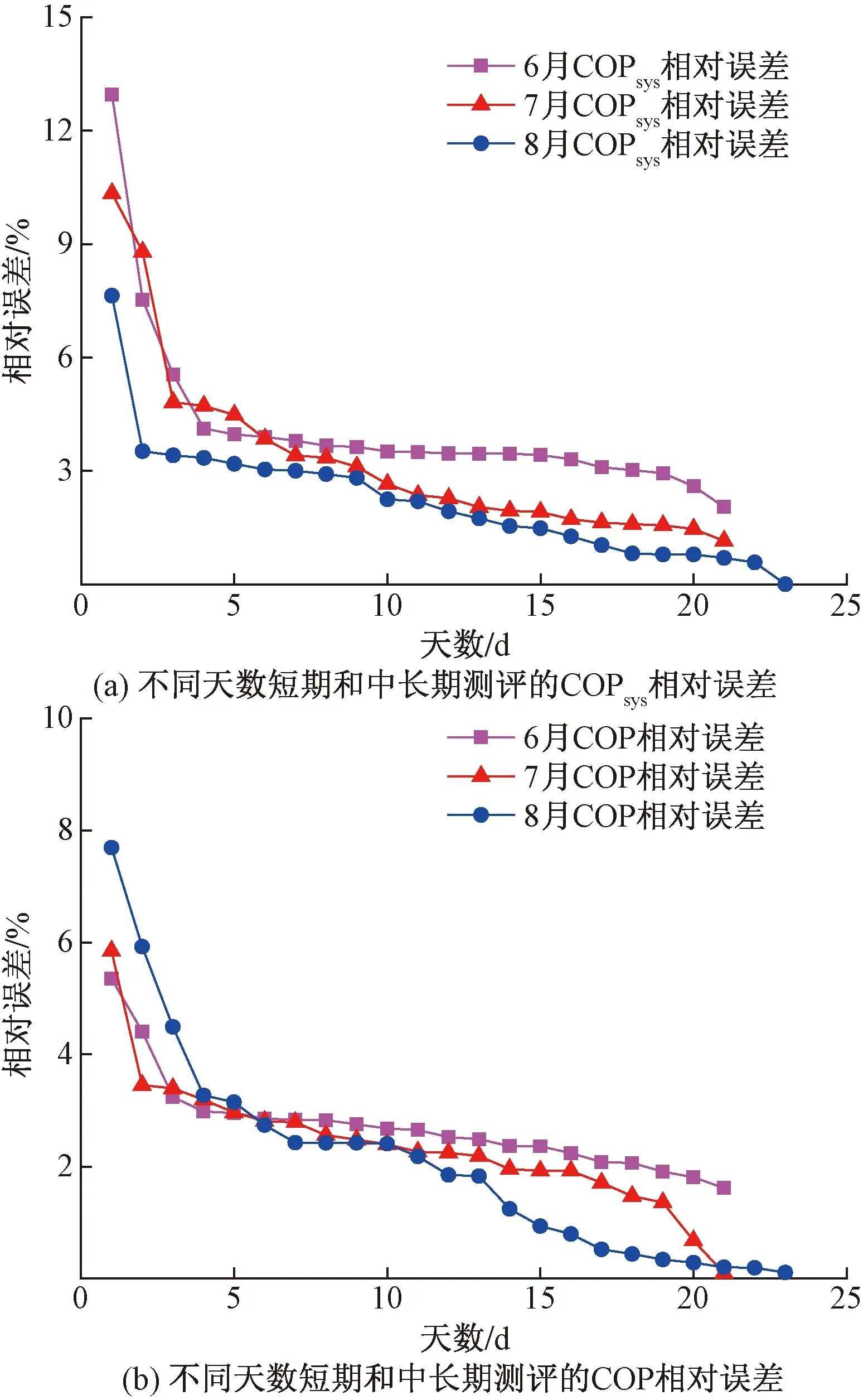
图8 不同天数短期和中长期测评的能效比相对误差Fig.8 Relative error of energy efficiency ratio between short-term and mid-to long term evaluation in different days
图8给出的6月、7月、8月不同天数短期测试的系统能效比和机组能效比的相对误差。由图8(a)可知,随着测试天数的增加,COPsys的相对误差逐渐减小。7、8月的COPsys测评相对误差比6月小,故可选取7月、8月中的10 d或6月的20 d进行短期测试产生的相对误差可控制在3%以内。图8(b)表明,COP的相对误差也呈现出逐渐减小趋势,因此COP的测评可选取6月、7月、8月中的13 d进行短期测试,所产生的相对误差可控制在3%以内,且8月继续累计测评COP相对误差逐渐减小至1%以内。综上所述,可选取7、8月累计13 d的短期COPsys及COP测试用于评估地源热泵系统低负荷率工况下的中长期夏季能效比。
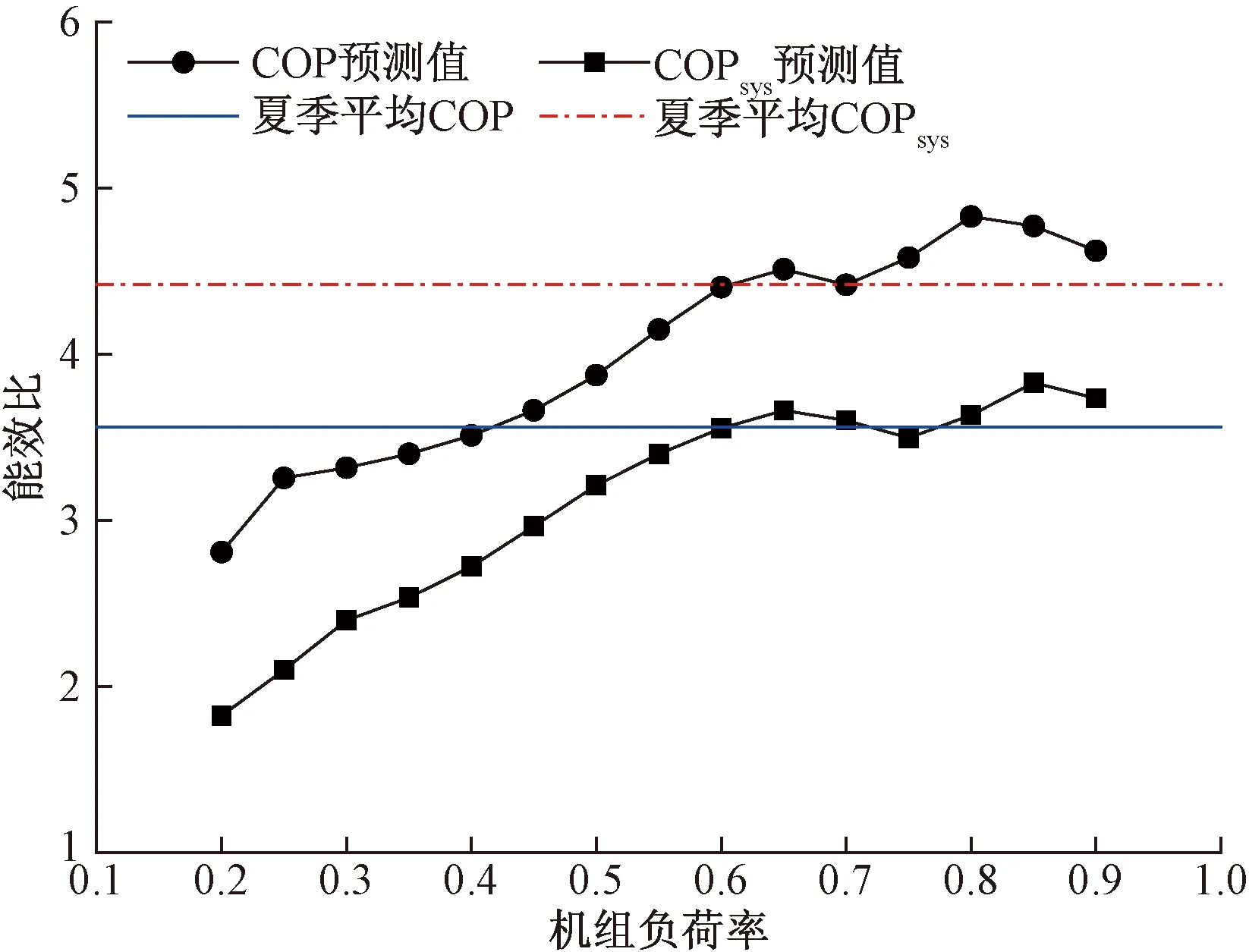
图9 不同机组负荷率的能效比Fig.9 Energy efficiency ratio in different unit load rates
上述运用短期测评来预测中长期COPsys及COP的分析中,采用预测相对误差较小时的机组负荷率(即60%~80%),考虑到机组负荷率为COPsys及COP第一影响因子,故进一步从机组负荷率范围扩大至20%~80%,考察机组负荷率对地源热泵系统COPsys及COP的影响,结果如图9所示。随着机组负荷率的增加,GA-BP模型预测的COPsys及COP逐渐增加,当机组负荷率达到55%时,能效比增加的速率减缓,继续增加机组负荷率,COPsys及COP均出现了先降低再增加的现象。当机组负荷率达到60%~70%时,COPsys及COP预测值最接近夏季平均COPsys及COP。由此也揭示了与图7相同的结论,选取机组负荷率为60%~70%时,可以采用GA-BP模型进行COPsys及COP的短期测评,且能满足测评误差要求。
6 结论
基于桂林地区地源热泵示范项目在夏季工况运行的实测数据,采用遗传算法优化BP神经网络模型预测了地源热泵系统COPsys及COP,并分析了其短期测试与中长期能效比预测的关系,得出了以下结论:
(1)对于地源热泵夏季运行工况下COPsys及COP的预测,GA-BP神经网络模型比BPNN模型预测精度更高。GA-BP预测的COPsys及COP与计算值的相对误差为±5%,各项预测误差评价指标更小。
(2)地源热泵夏季中长期能效比评估选取的最佳短期测评时间为一天当中14:00—16:00和7月、8月累计不小于13 d测评COPsys及COP,其能效测评产生的相对误差在合理的范围内。
(3)当其他特征参数保持不变,机组负荷率达到60%~70%时,GA-BP模型预测的COPsys及COP最接近夏季平均COPsys及COP,可以将此预测值作为中长期能效测评值,且预测误差较小。
(4)桂林岩溶地区地源热泵系统在系统低负荷率工况下运行可通过短期实测参数应用GA-BP神经网络预测模型进行中长期地源热泵系统能效比预测,为地源热泵系统在桂林地区的推广应用提供实践参考。
