高精度应变式三维力传感器研究*

骆训煌, 周兴林, 关佳希, 朱 攀, 张海峰

(武汉科技大学 机械自动化学院,湖北 武汉 430081)

0 引 言

三维力传感器因其能检测三维空间中多个方向的力信息,在实际工程测量中得到了广泛的运用[1]。三维力传感器按不同的工作原理可划分为电阻式、电感式、电容式及光纤光栅等[2]。在弹性体结构设计上,传统三维力传感器常采用筒式、柱式、环式、悬臂梁等结构[3]。实际工程测量中往往需要维间耦合小、测量精度高、结构简单、便于制造的多维力传感器,例如车辆轮胎—路面三维接触力大小测量。

本文提出一种用于测量空间三维力的应变式三维力传感器结构。运用有限元分析确定应变片在弹性体结构中的最佳贴片位置,针对电阻应变片变形时阻值的微小变化不能直接被模数(A/D)转换且信噪很大的问题,设计了应变测量调理电路。解耦计算表明,所研制的传感器维间耦合误差较小,具有较高测量精度,满足实际大多场合三维力测量精度需求。

1 传感器结构

应变式三维力传感器结构如图1所示。在弹性体的上半部分受力部位的侧壁上开设有4个贯穿径向且大小相同的结构孔,孔与孔之间彼此相邻90°,在两结构孔之间的侧壁上粘贴应变片。

图1 三维力传感器结构

弹性体侧壁上粘贴有4个电阻应变片。区间一、三位置分别粘贴应变片A,C,区间二位置粘贴应变片B,区间二相对位置粘贴应变片D。其中,应变片A,C用于测量X方向上的作用力FX。当传感器弹性体受到力FX作用时,应变片A,C产生弯曲变形,应变片A受压变形,受到压应力作用,应变片C受拉变形,受拉应力,因此，应变片A,C的上下贴片处的阻值会发生相应的变化。同理,当力FY作用时,电阻应变片B,D方向上产生弯曲变形,其中，应变片B受到压应力,应变片D受到拉应力。当力FZ作用时,4片应变片均受到拉应力作用。

因此,在受到X或Y方向上力作用时,4片应变片总是有2片应变片的应变方向相反,均为一正一负,而另外两片应变片敏感栅敏感方向垂直于所受外力方向。由于横向效应引起的应变量极小,且理论上另外2片电阻应变片的应变输出正负相抵消,可以当作是应变片对Z方向上的力不敏感,因此，可以用4个1/4单臂电桥测得电压之和得到Z方向上的力值大小。图2所示为测量电桥[4]。

图2 应变片1/4单臂惠斯通电桥

2 有限元分析

利用有限元软件Ansys对传感器弹性体进行应变分析。将可能影响有限元分析精度的传感器倒角进行简化去除,选取六面体网格划分技术,网格尺寸大小设置为1 mm。弹性体材料选用316L不锈钢,其结构参数见表1所示。

表1 316L不锈钢材料参数

根据传感器弹性体实际安装要求,将传感器弹性体下底面施加面约束,在弹性体上端面中心处施加三方向满载集中力FX,FY和FZ,力值大小为500 N。图3所示是传感器弹性体在三方向受力时的应变分布图。

图3 弹性体受力时应变分布

分析图3可知,对于以上三种受力情况,在X方向受力时弹性体产生最大应变,最大应变为ε=4.43×10-4,ε·E=88.6 MPa,远小于316 L不锈钢的屈服强度170 MPa,说明具有该弹性体结构的传感器是安全的。

为了得到较高的灵敏度及其稳定性,需要选择最佳的应变片粘贴位置。利用Ansys分析后处理其提供的路径映射技术,分析弹性体各节点的应变大小。选取弹性体受力时应变片粘贴处的侧壁为分析对象,选择各侧壁外表面的中心处沿着中心线的位置定义路径,将整个侧壁的高度作为该路径的定义区间,分析得到各个路径区间的节点应变关系,如图4所示。其中,横坐标表示该定义路径中各节点距离中心线原点各点的距离,单位为mm,纵坐标表示各节点沿Z方向对应的应变值[5]。

图4 各路径区间节点的应变分布

由图4可知,在单维力FX和FY的作用下,路径一区间和路径二区间在1～15 mm区间内的应变值较大。在力FZ的作用下,路径三区间在5～25 mm区间节点应变值较大。综上分析,选取区间段1～15 mm包含于整个应变片敏感栅粘贴区域。因此,该应变式三维力传感器的贴片区域为1～15 mm。

3 调理电路设计

应变式多维力传感器属于高内阻传感器,通过粘贴在试件表面的电阻应变片的阻值变化确定作用力的变化。电阻应变片经惠斯通电桥转换后的电压量仍然是微弱信号,不便于后续的分析和利用,且不能直接进行A/D模数转换；同时,电阻应变式力传感器的输出信号还掺杂着噪声信号。本文选取AD620作为仪表放大器。AD620是一种低成本、高精度的仪表放大器,其采用经典的三运放改进设计,通过调整片内电阻的绝对值,只需要一个外接电阻就可以实现对增益的精确编程[6]。图5所示为前置放大电路。本文外接增益电阻阻值大小为499 Ω,电压信号放大倍数可达100倍。

图5 放大电路

本文选取的OP07是一种高精度的运算放大器,具有极低的输入失调电压,与电阻和电容组成有源低通滤波电路,具有放大功能[7]。滤波电路如图6所示。

图6 滤波电路

在电路中,由于滤波电路的输出阻抗较大,通常利用电压跟随器进行缓冲作用,降低输出阻抗的大小[8]。电压跟随器连接A/D转换电路如图7所示。

图7 电压跟随电路

4 维间耦合分析

依次在该三维力传感器弹性体结构上表面中心处施加三方向大小相等满载集中力,力值FX=FY=FZ=200 N,计算得到4个应变片的应变输出结果如表2所示。

表2 应变片A,B,C和D的应变量

分析表2中数据,X方向力主要作用于应变片A和应变片C,应变片B和应变片D受到的影响很小,且应变片A,C的应变值的绝对值大小几乎相等,符号相反,表明着X方向力作用时,应变片A处在压缩状态,应变片C处在拉伸状态。Y方向力主要作用于应变片B和应变片D,应变片A和应变片C受到的影响很小,且应变片B,D的应变值的绝对值大小几乎相等,符号相反,表明着Y方向力作用时,应变片B处在压缩状态,应变片D处在拉伸状态。Z向力均对应变片A,B,C,D有较大影响,4个应变片的应变值的绝对值大小几乎相等,符号相同,均为负号,表明Z方向力作用时,四片应变片均处在压缩状态。故可将应变片C和应变片A的应变量作差得到的应变值作为载荷FX作用下的应变εx；将应变片D和应变片B的应变量作差得到的应变值作为载荷FY作用下的应变εy；将应变片A,B,C和D的应变量相加之和得到的应变值作为载荷FZ作用下的应变εz。有限元分析结果与理论设计相同,表明该应变式三维力传感器有3组桥路输出且具有三维力解耦性。

由于维间耦合问题的影响,力传感器中的各应变输出不是相互独立的,因此,桥路的电压信号输出变化量与弹性体的受力关系为

(1)

式中 ΔU为桥路三方向的电压信号输出变量,K为耦合矩阵,kxy的物理意义为Y方向的力载荷在X方向的电压信号输出变化量,F为三方向力变量。依次在X,Y,Z三方向上加载几组已知力载荷,依次求出每个方向的力载荷对应的三方向的应变输出,将9组数据拟合成一次函数直线,求取每条直线的斜率即为耦合矩阵中的各个元素。

按照所设计的调理电路利用示波器和LabVIEW编写的传感器输出信号采集程序显示不同力值大小的载荷作用下的输出电压信号。输出电压信号采集及显示装置如图8所示。

图8 输出电压信号显示

记录每次不同方向上的各组不同力值载荷作用下的输出电压信号值,考虑到各组电压输出信号值求取精度,选择最小二乘法拟合解耦。通过线性拟合得出传感器输出曲线斜率即为所求的耦合矩阵,从而可以计算出该应变式三维力传感器的各个方向上的耦合误差。三方向受载时各方向输出信号如图9所示。

图9 三方向电压输出信号

由图9可知,传感器在X轴向的线性度较高,各方向的维间耦合较小。计算图9中拟合直线斜率,得到

kxx=-1.140 33,kyk=0.000 07,kzx=0.000 14,

kxy=-0.000 51,kyy=1.147 33,kzy=-0.000 75,

kxz=0.000 09,kyz=0.003 6,kzz=0.101 42

因此,各桥路的电压信号输出变化量与弹性体的受力关系为

(2)

由式(2)可知,当已知作用在传感器弹性体上的三方向力载荷时,可以求出三维信号变化量,同理,亦可以通过测量的信号变化量反推出三维作用力的大小,将式(2)等号两边同时左乘耦合矩阵K的逆矩阵K-1,得

(3)

根据式(3)得出的解耦矩阵,可以计算求出该应变式三维力传感器维间耦合误差[9]

(4)

计算结果表明,该应变式三维力传感器的维间耦合误差较小,最大的耦合误差出现在力FZ作用时,耦合误差仅为0.877 5 % FS。相较于其他应变式多维力传感器的最大维间耦合误差1.14 %FS和3.56 %FS[10]来说,该应变式三维力传感器的最大维间干扰误差大大减小。

将计算求得的耦合矩阵进行解耦验证。在传感器X,Y,Z三方向上施加一定值载荷,根据实际电压的测量值与上式计算得出的理论值对比,得到的测量结果如表3所示。

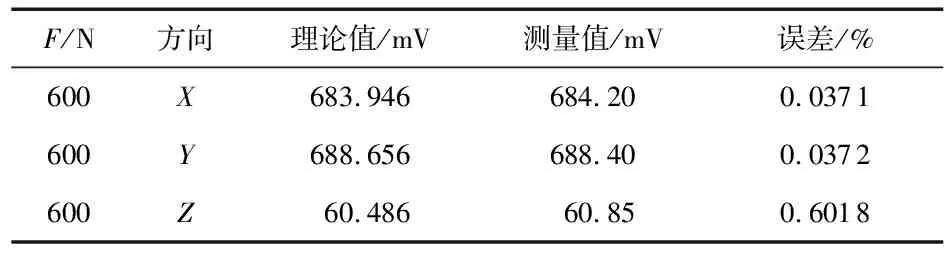
表3 力传感器解耦结果

由表3数据可知,该应变式三维力传感器对X,Y,Z三方向力测量误差较小,最大误差仅为0.601 8 %,满足实际大多场合三维力测量精度需求。

5 结 论

1)提出了一种应变式三维力传感器弹性体结构,通过在弹性体上半部分结构孔的4个侧壁上粘贴电阻应变片,利用4个1/4单臂电桥来测量X，Y，Z三方向力的大小；

2)通过有限元仿真分析,确定传感器弹性体各部分受力状况,得出弹性体应变数据,利用路径映射技术确定应变片在弹性体上的最佳贴片位置,并判断了该传感器的力解耦性能；

3)设计了针对该应变式三维力传感器的调理电路,利用LabVIEW编写的传感器输出信号采集程序显示不同力值大小的载荷作用下的输出电压信号,分析并计算求得该三维力传感器的耦合矩阵,计算得出该传感器的维间耦合误差较小,最大的耦合误差出现在力FZ作用时,耦合误差仅为0.877 5 % FS。解耦验证分析表明,所研制的传感器具有较高精度,满足实际大多场合三维力测量精度需求。