间歇牵制控制下非线性多智能体系统的滞后一致性

黎美华， 李丰兵， 马忠军

(桂林电子科技大学 数学与计算科学学院，广西 桂林 541004)

近年来，多智能体系统的一致性问题越来越受到人们的关注，如社会学、生物学、传播学、控制工程和计算机科学等。许多有效的控制策略被用来使多智能体系统能够达成一致，包括自适应控制[1]、间歇控制[2-7]、脉冲控制[8]、牵制控制[9-15]和反馈控制[16]。由于大型控制网络的节点数量巨大，对所有节点施加连续控制往往是不可能的(成本太高或实际条件不允许)。为此，间歇控制协议和牵制控制协议越来越受到人们的重视。Liu等[2]通过添加一些间歇牵制控制器来研究线性耦合无延迟网络的聚类同步问题。文献[3-5]通过不同方法研究周期间歇牵制控制的时延网络实现同步问题。文献[6-7]通过引入周期性间歇控制方法，分别研究了非线性系统的稳定性和混沌系统的同步问题。

网络中的信息流通常不是瞬时的，其中时延普遍存在。以往的工作主要研究时延对智能体系统收敛性的影响[17-19]。文献[20]提出了滞后一致性的概念，滞后一致意味着跟随者的相应状态向量在领导者后有一个时延。此后，一些学者进行了一系列滞后一致性的研究[21-25]。Wang等[21]提出了一种基于邻居和领导者局部信息的控制算法，解决非线性多智能体系统的滞后一致性问题,此外，还考虑了具有自适应反馈控制下的非线性多智能体系统的滞后一致性。Zhou等[22]研究了具有有界外部扰动的二阶多智能体网络的有限时间滞后一致性问题,通过构造一种新的具有速度和位置相对信息的协商一致控制协议，使多智能体网络在有限时间内实现滞后一致。Hu等[23]考虑了在分布式自适应控制协议下的领导跟随多智能体系统的滞后一致性问题，运用Lyapunov稳定性理论, 给出了系统能够实现滞后一致的充分条件。Wang等[24]应用Lyapunov泛函和矩阵理论分析了非线性多智能体系统在牵制控制下的滞后一致性。Ni等[25]研究了具有输入延迟的二阶领导-跟随多智能体系统在固定时间内的滞后一致性问题。

目前,尚未有非线性多智能体系统在间歇牵制控制下滞后一致性的相关研究。鉴于此，给出间歇牵制控制协议，并运用矩阵不等式、泛函微分方程理论和稳定性理论，导出该系统在非周期间歇牵制控制下实现滞后一致的充分条件。

1 预备知识

1.1 图论

设G=(V,ε,A)为N阶加权的有向图，其中V={1,2,…,N}表示节点集，节点之间的连接边构成的集合为ε⊆V×V，A=(aij)N×N为G的加权邻接矩阵。图G的有向边记为εij=(i,j)，表示节点i能收到来自节点j的信息。aij>0当且仅当G有有向边(i,j)，否则aij=0。若有向图G的某个节点按照有向路径可以到达所有其他节点，则有向图G具有一个生成树。若有向图G的任意2个不同节点i和j都存在i到j的有向路径，同时也存在j到i的有向路径，则称有向图G是强连通的。Ni为节点i的邻居节点集，即Ni={j∈V:(i,j)∈ε}。L= (lij)N×N为有向图G的拉普拉斯矩阵，且

1.2 模型描述

考虑一个具有N个跟随者的多智能体系统，其中每个跟随智能体的动力学模型为

(1)

其中：xi(t)∈Rn,ui(t)∈Rn，i=1,2,…,N，分别为第i个智能体的位移变量和控制输入；f∶Rn→Rn为连续映射，表示第i个智能体自身非线性动力学；c为位移的耦合强度。邻接矩阵A=(aij)∈RN×N描述系统(1)的网络通信拓扑，若第i个智能体能收到第j个智能体的信息，则aij>0，否则aij=0。

领导者智能体的动力学模型为

(2)

x0=(x01,x02,…,x0n)Τ∈Rn为领导者智能体的位移变量，f(x0)=(f1(x0),f2(x0),…,fn(x0))Τ∈Rn为领导智能体的自身动力学。

非周期间歇牵制控制协议为

(3)

其中k∈N。若第i个智能体能收到来自领导者智能体的通讯信息，则bi>0，否则bi=0。

定义1[20]若存在常数τ2>0，使得

(4)

其中i=1,2,…,N，则称系统(1)和(2)能实现滞后一致。

假设1存在非负常数ρ，使得

‖f(x(t-τ1),x(t))-f(x0(t-τ1-τ2),

x0(t-τ2))‖≤ρ[‖x(t-τ1)-

x0(t-τ1-τ2)‖+‖x(t)-x0(t-τ2)‖]，

(5)

其中，

x(t-τ1),x(t),x0(t-τ1-τ2),x0(t-τ2)∈Rn。

假设2[26]存在2个正常数0<θ<ω<+∞，对于k=1,2,…，使得

(6)

定义2[26]对于非周期间歇牵制控制协议，定义休息宽度tk+1-sk在时间跨度tk+1-tk上的最大比值为

(7)

显然，0<Ψ<1。由于Ψ=0是连续情形，通常假设Ψ∈(0,1)。

(8)

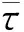
a1>a2≥0,δ=a1+a3>0,σ=λ-δΨ>0，

(9)

则

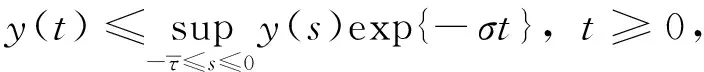
(10)

其中λ>0为方程

的唯一正解。

2 主要结论

具有非周期间歇牵制控制协议(3)的第i个跟随者智能体系统(1)可描述为

(11)

其中xi(t)∈Rn为第i个智能体的位移状态变量，i=1,2,…,N。

令位移状态误差

ei(t)=xi(t)-x0(t-τ2)，

则第i个误差系统可写为

(12)

误差系统用向量形式可表示为

(13)

e(t)= (e1(t)Τ,e2(t)Τ,…,eN(t)Τ)Τ∈RNn×1,

ei(t)= (ei1(t),…,ein(t))Τ=

(xi1-x01,…,xin-x0n)Τ∈Rn×1，

i=1,2,…,N，其中：xij为第i个智能体的第j个分量；

H=L+diag(b1,b2,…,bN)。

定理1若假设1成立，并存在一个正定矩阵H及

α1=-(3ρ-2cλmin(H)),

α2=3ρ-2cλmin(L),α1>ρ≥0,

δ=α1+α2>0,λ-δΨ>0,

证明定义Lyapunov函数

(14)

易知，V(t)≥0，若V(t)=0，当且仅当e(t)=0Nn×1。

当t∈[tk,sk],k∈N时，将V(t)沿式(13)的轨迹对时间t求导，可得

eΤ(t)[F(e(t))-c(H⊗In)e(t)]≤

ceΤ(t)(H⊗In)e(t)≤

ceΤ(t)(H⊗In)e(t)≤

βV(t-τ1)，

(15)

其中，

α1=-(3ρ-2cλmin(H)),β=ρ。

适当选取c的值，可使α1>0,β>0。

当t∈(sk,tk+1),k∈N时，采用类似分析方法将V(t)沿式(13)的轨迹对时间t求导，可得

eΤ(t)[F(e(t))-c(L⊗In)e(t)]≤

ceΤ(t)(L⊗In)e(t)≤

ceΤ(t)(L⊗In)e(t)≤

(16)

其中，α2=3ρ-2cλmin(L),β=ρ,且α1+α2>0。结合式(15)、(16)，可得

(17)

基于上述分析，由引理2易导出：

即多智能体系统(1)和(2)在非周期间歇牵制控制协议(3)下可实现滞后一致。证明完毕。

推论1若假设2成立，且

μ=λ(θ-τ1)-κ(ω-θ)>0,

其中κ=α2+ρ，ρ为假设1中的定义，θ和ω为假设2中的定义，λ和α2为定理1中的定义，则多智能体系统(1)、(2)在非周期间歇牵制控制协议(3)下可以实现滞后一致。

证明类似于文献[26],由于

因此，多智能体系统(1)和(2)在非周期间歇牵制控制协议(3)下可实现滞后一致。

3 数值模拟

对于多智能体系统(11)，考虑1个领导者和4个跟随者，其网络拓扑图如图1所示，其中：0为领导者；1、2、3、4为4个跟随者。非线性函数f可由蔡氏电路[27]表示为

(18)

其中：

α=10,β=17.53,γ=0.163 6,a=-1.432 5,b=-0.783 1,ε=0.2,η=0.5,通讯时滞τ1=0.02。初始条件取[0,1]上不同常数函数(t∈[-0.02,0])时，系统(18)存在混沌吸引子，如图2所示。

图2 蔡氏电路系统(18)的混沌吸引子

由网络拓扑图可得G的Laplace矩阵：

令B=diag(5,0,0,0)，由Laplace矩阵可知，只有第1个智能体能接收到领导者的信息。对于间歇控制，定义非周期间歇控制为

[0,0.2]∪[0.5,0.8]∪[1,1.2]∪[1.5,1.8]∪

[2.0,2.2]∪[2.5,2.8]∪[3.0,3.2]…。

对于定理1中的矩阵H，取ρ=0.1，c=0.1，则

α1=-(3ρ-2cλmin(H))=0.5，α1>ρ≥0，

α2=3ρ-2cλmin(L)=0.3，

δ=α1+α2=0.8>0，λ=0.4，ψ=0.4，

λ-δψ=λ-0.32=0.08>0。

由于满足定理1中的所有条件，多智能体系统(1)和(2)能实现滞后一致。由数值模拟得出领导者和4个跟随者的滞后误差曲线如图3所示。从图3可看出，系统(1)与(2)之间相应变量的对应分量的滞后误差随时间趋于无穷大而趋于0。

图3 滞后误差变量随时间的演化(i=1,2,3,4)

4 结束语

研究了一阶非线性多智能体系统在非周期间歇牵制控制下的滞后一致性问题。非周期间歇牵制控制的多智能体系统只需在每个区间的某个时间段内进行牵制，而不是整个区间，以确保系统达到滞后一致，从而节约资源和降低成本。此外，与以往文献不同，延迟是自然引入的，使得整体动态模型成为泛函微分方程。利用Lyapunov函数方法导出了多智能体系统实现滞后一致的充分条件。由于通信时延通常是时变的，今后将研究受时变通信时延影响的多智能体系统的滞后一致性问题。