基于深度强化学习算法的车辆行为决策研究

陈名松， 张泽功， 吴冉冉， 吴泳蓉

(桂林电子科技大学 信息与通信学院,广西 桂林 541004)

近年来，随着经济发展和科技进步，我国城市居民汽车保有量持续增长，据国家统计局发布的2018国民经济和社会发展统计公报显示，2019年末全国民用私家车保有量达2.07亿，比上年末增长9.37%。然而，汽车出行方便了日常生活的同时也带来了一系列问题，据国家统计局数据显示，2018年我国汽车交通事故发生数达到24.5万起，造成人员伤亡23.5万人次，直接财产损失13亿8 456万元。另有研究表明，驾驶员失误导致的交通事故占交通事故总量的90%，主要因素有驾驶员分心、注意力不集中和疲劳驾驶等[1]。所以对于自动驾驶的研究成为一个热点方向，谷歌、百度、AMD等企业及国内外研究人员均对此进行了相关研究。

自动驾驶是指车辆通过感知周围环境并在无人工干预情况下进行自主驾驶的行为。首先车辆要感知周围环境，识别驾驶环境中的行人、车辆、车道等信息。这一过程通常通过计算机视觉技术进行处理，通过对图像进行获取、处理、分析和理解等一系列步骤将现实世界中的高维度特征转换成数字信息并输入一个策略模型中，在动态的环境信息中，尝试得到奖励值最大的驾驶行为，实现最佳的决策。DQN算法[2]是深度强化学习算法的开山之作，它与自动驾驶技术的整合研究是一种非常流行且有效的方式。2015年，Mnih等利用卷积神经网络计算Q函数，并利用该框架在Atari 2600游戏中成功达到超过职业玩家的水平。2016年，Bojarski团队使用卷积神经网络进行端到端自动驾驶系统的研究，通过将摄像头获取的数据送入CNN进行训练，从而实现对方向盘的控制。Sallab团队[3]利用DQN算法进行了车道保持辅助系统的仿真研究，通过对比实验分析了不同终止条件下训练得到的策略的区别。2017年，Chae等[4]利用DQN进行自主刹车系统研究，在经过7万多次模拟试验后，Agent可以学习到自主刹车的能力。夏伟等[5]提出了结合聚类算法和DQN算法的自动驾驶策略学习模型，也取得了一定效果。

虽然DQN在不同的模拟器上通过离散化方向盘和刹车等行为实现了对自动驾驶的模拟，但是DQN的本质依然与传统的强化学习一样旨在解决离散和低维动作空间，它会产生大量的状态-动作对，不适用于像油门、刹车和方向盘这样的连续动作空间。即使通过离散化将DQN应用于连续域也会引起维度灾难等问题，不利于后续计算。针对上述问题，深度确定性策略梯度算法[6](deep deterministic policy gradient，简称DDPG)应运而生。DDPG算法是一种无模型、异策略的算法，它结合了DQN算法、A-C方法和DPG算法，在连续域控制问题上具有良好的表现，引起了学者们的广泛关注。张斌等[7]将DDPG算法与策略动作过滤相结合，通过将策略网络的多输出改为单输出来控制油门和刹车，降低了自动驾驶中的非法策略比。吴俊塔等[8]通过基于DDPG算法的多个子策略平均集成的方式进行自动驾驶行为的控制。

1 基于深度强化学习的自动驾驶模型

1.1 强化学习模型

强化学习是机器学习的一个分支，智能体Agent通过与环境的不断交互学习，提高Agent对于未知环境的探索和适应能力，从环境探索中得到最大回报，从而学习到完整策略[7]。强化学习就是给一个马尔科夫决策过程(MDP)寻找最优策略π，使得该策略下的累计回报期望最大。

所谓策略指状态到动作的映射，即：

πθ(a|s)=p[At=a|St=s,θ]，

(1)

表示在状态s下指定一个动作a的概率。若策略是确定的，则给定一个确切动作。整个MDP过程可以用五元组(S,A,P,R,γ)表示，其中S为有限状态集合，A为有限动作集合，P为状态转移概率，R为回报函数，γ∈[0，1]为折扣因子。当Agent与环境进行交互，在状态st处的累计回报为

(2)

为了评价状态s的价值和求解最优策略，引入状态值函数υπ(s)和状态-行为值函数qπ(s,a)，实际应用中采用其贝尔曼方程：

υπ(s)=Eπ(Rt+1+γυπSt+1|St=s)，

(3)

Qπ(s,a)=Eπ[Rt+1+γQ(St+1,At+1)|St=s,At=a]。

(4)

求解上述值函数有2种方法：基于表的方法和基于值函数逼近的方法[9]。基于表的方法包括传统Q-learning和Sarsa算法，该类算法因为无法构建足够大的Q值表，所以其应用局限于状态-动作空间很小的情况。为了解决上述问题，DeepMind公司利用神经网络来逼近状态值函数，提出了结合深度学习和强化学习的DQN[10]算法，从而完整地表示了状态-动作空间。

1.2 基于DDPG算法的行为决策框架

1.2.1 DPG算法

DPG算法[11]即确定性行为策略，根据式(1)定义了一个策略网络。策略网络的输入是环境信息S，包括车辆距离车道的距离、车辆速度等，输出为车辆要进行的下一步动作a，包括转向、刹车、油门等控制信息，每步的行为通过策略函数直接获得确定值，该策略网络的目标函数定义为

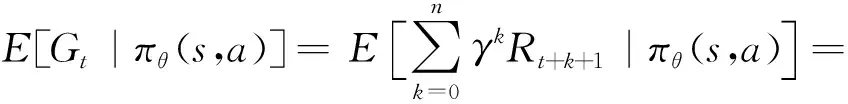
Ex～p(x|θ)[R]。

(5)

其中策略网络的目标函数梯度是状态-行为值函数梯度的期望，如式(6)所示，这样可以在不考虑动作空间维度的情况下更好地估计策略网络目标函数的梯度，提高了计算效率。

(6)

1.2.2 DQN算法

DQN算法是第一个深度强化学习算法，其利用神经网络对状态-行为值函数进行拟合，状态-行为值函数可表示为

Qπ(S,a)≈Q(s,a,w)，

(7)

其中ω为神经网络的的权重，结合式(6)，可得DDPG算法：

(8)

1.2.3 DDPG算法流程

DDPG算法将上述2种算法进行了融合，如图1所示，该算法由Actor(策略)模块、Critic(评价)模块和经验池组成。其中Actor和Critic模块分别利用神经网络对策略函数和Q函数进行拟合。同时，由于Actor网络与环境交互所产生的时间序列是高度相关的，直接利用这些数据进行网络训练会导致网络过拟合，不易收敛。因此，借鉴DQN算法，引入了经验回放机制(experience replay)，通过在经验池中进行随机批量取样对网络进行训练，解决了上述问题。

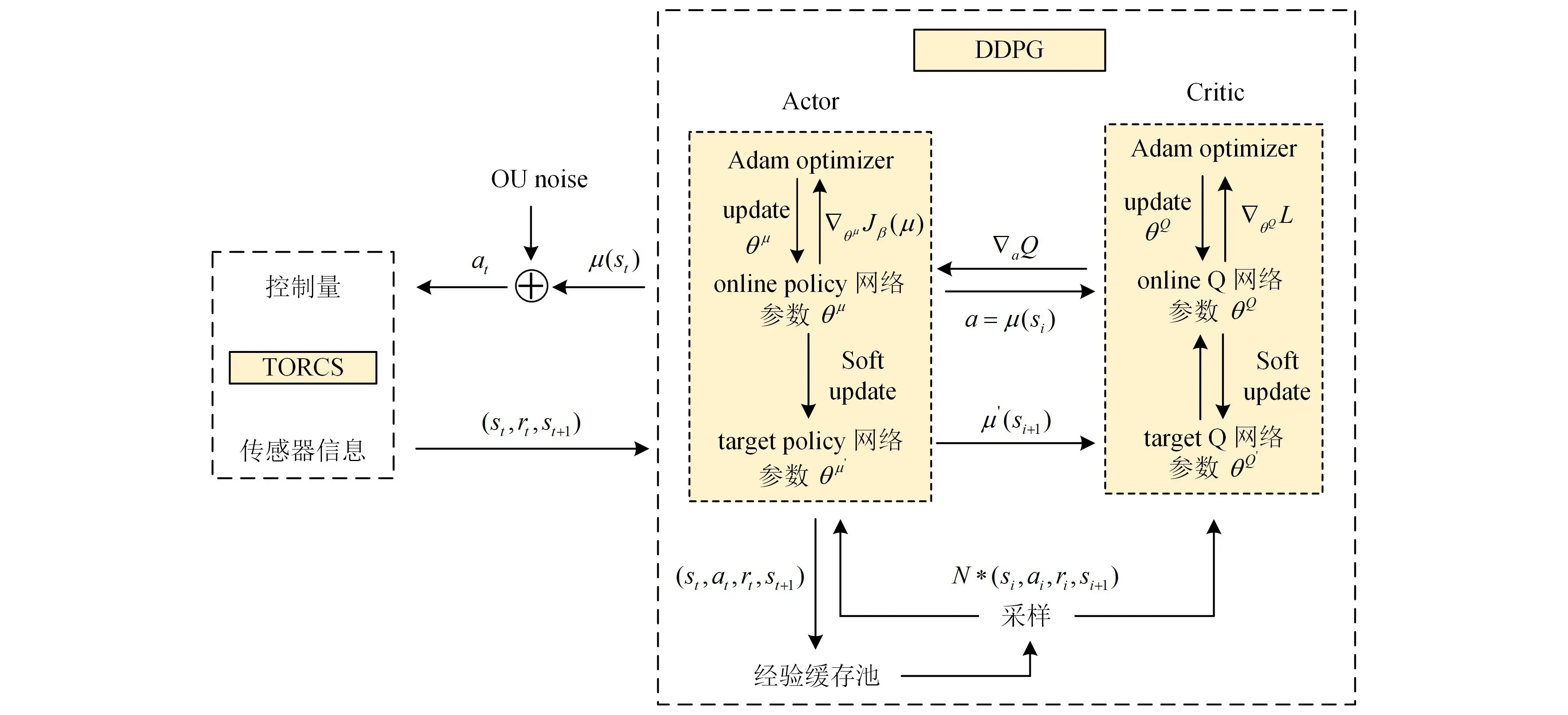
图1 基于DDPG算法的车辆决策流程

Actor-Critic方法将策略梯度算法和值函数结合在一起。Actor网络产生当前策略，输出动作；Critic网络对该动作进行评判。然后，基于此评判，Actor网络调整其网络权重，使得输出的动作在下一次变得更好。为提高算法训练的稳定性，DDPG中引入了Target-Actor网络和Target-Critic网络，初始结构和参数均与其对应的Actor和Critic网络一致，后续则根据式(9)即图中的Soft Update进行参数更新，其中θQ、θQ′、θπ、θπ′分别为Target-Critic网络、Critic网络、Target-Actor网络和Actor网络的参数。

(9)

2 改进的DDPG算法

为提高算法的训练效率和网络的稳定性，针对传统DDPG算法提出以下几点改进，主要包括将引导学习和优选经验回放结合，以下称之为LS-DDPG。

2.1 引导式学习

一般而言，新手在完成一项任务时，需要具有经验的师傅对其进行指导，这样完成任务的效率和准确率会比独自探索高很多。受此启发，在利用传统DDPG算法对TORCS中的车辆进行自动控制时，引入一个专业的控制器，将其作为“老师”来引导，进行网络预训练。传统DDPG算法对于Critic网络的训练是通过随机抽取经验缓存池中的经验样本数据并送入Critic网络中进行批训练，经验数据根据回报函数得到评估值Q。对于Actor网络的训练过程则是利用环境信息S对动作a的梯度来进行训练。

引导式学习的DDPG算法对于网络的训练包括预训练和正常训练2个阶段。预训练阶段不涉及强化学习的内容，仅利用专业控制器来进行网络训练，得到一个预训练模型。在后期强化学习的正式训练中，先加载此预训练模型进行Agent与环境的交互，通过采取特定策略，使得训练前期预训练模型在动作的输出方面占主导，然后逐渐减少预训练模型的主导作用，Actor网络逐渐占据主导。这样允许Actor网络在学习引导行为的同时可以探索更多引导行为之外的动作。

2.2 优选经验回放

传统DDPG算法利用经验回放机制将Agent与环境交互得到的经验样本存储到经验缓存池中，然后通过随机抽取BATCH_SIZE数据进行Actor网络和Critic网络。这种处理方式消除了经验样本之间的相关性，提高了网络训练的稳定性。但由于经验样本的选取是随机的，选取的经验样本质量参差不齐，网络训练速度和效率较低。为解决此问题，Schaul等[12]提出了优先经验缓存机制(prioritized experience replay)，通过计算TD-error得到经验样本的重要程度，将重要程度较大的数据送入神经网络进行训练。这种算法对于加速神经网络的收敛有一定作用，但是算法复杂度较高。本着不提升算法复杂度同时提高神经网络的训练效率的原则，利用经验池分离原则，采用优选经验样本回放的方式对DDPG算法进行改进。

1)经验样本分离存储。优选经验样本回放需要通过设置阈值区分样本的优劣，然后分别存入不同的经验池。劣势样本包括脱离轨道的经验样本、发生碰撞的经验样本以及rt为负值的经验样本等。同时，根据对应测试的赛道宽度d和车身宽度l设置经验存放阈值dth=(d-l)/d。车辆行驶在赛道阈值以外所得到的经验被认定为劣势样本，反之则为优势样本。

2)调整经验样本抽取比例。按一定比例α从不同的经验池抽取经验样本，在1个批处理样本中2类样本必须同时存在，以防止神经网络达到局部最优。同时优势样本与劣势样本的抽取比例α随着当前训练步数的增加而逐渐降低，防止Agent学习到的策略网络过拟合。

3)降低策略网络和目标网络的更新频率。DDPG算法涉及到了2个神经网络，且每次都在连续状态中更新参数，每次参数更新前后都存在相关性。若评价网络某次评价产生过估计的情况，则在利用差分误差进行频繁的网络参数更新时会导致误差累积放大，策略更新向着发散的方向进行，不利于算法收敛。因此，应该控制策略网络和目标网络的更新频率低于评价网络，即在进行策略网络更新前，最小化估计误差。

2.3 LS-DDPG算法流程

主网络和目标网络的参数初始化方式均为随机初始化，OU噪声的添加会随着训练步数的增加而改变，是一个线性改变的过程，这样可以控制预训练权重和策略网络的主导比重。LS-DDPG算法伪代码如下。

1：初始化Actor网络π(s,θπ)和Critic网络Q(st,at,θQ), 经验池大小N, BATCH_SIZE大小M;

2：初始化Target-Actor网络π′(s,θπ′)和Target-Critic网络Q′(st,at,θQ′);

3：创建经验缓存池Bs和Bf, 并设置经验缓存阈值dth, 加载预训练权重;

4：Episode循环开始:

5：选择始化状态st, 初始化OU噪声;

6：Step循环开始:

7：将OU噪声添加到动作策略中, Actor网络根据当前策略做出动作at;

8：将at送入TORCS环境中, 转化成车辆控制动作执行, 得到当前动作的回报值rt和新的环境值st+1;

9：根据rt是否大于0与当前环境信息中的车辆位置是否大于dth决定(st,at,rt,st+1,done)存入对应的经验池;

10：根据样本采样比例α, 在Bs和Bf分别采样数据, 采样数据总量为M;

11：通过Target-Critic网络计算当前动作的期望回报;

13：当Step到达设置的Actor网络的更新频率时:

15：利用式(9)更新Target网络;

16：结束Step循环;

17：结束Episode循环。

3 实验设计

3.1 实验运行环境

实验运行环境为Ubuntu 16.04，Python 3.6，Keras 2.1.6，Tensorflow 1.13.2，CUDA 10.0.130，CUDNN 7.5.0，gym，TORCS仿真平台，地图为A-Speedway地图。CPU为Intel i7 7800X，GPU为GTX 2080TI，运行内存32 GiB。

3.2 实验设计

实验中对于DDPG算法、LS-DDPG算法设计均采用2层隐藏层的全连接神经网络，隐藏单元数分别为600、300，而后actor网络紧接着的3个全连接层的输出分别对应智能体的转向、油门和刹车3个控制变量。转向的取值范围为[-1,1]，分别代表向左到底和向右到底；油门和刹车的取值范围为[0,1]，分别代表不踩踏板和将踏板踩到底。算法中将以下函数作为奖励函数：

r=(1-tracPos)(Vxcosθ-Vx|sinθ|-

(10)

网络训练均以当前赛道的10圈作为目标，而后分析算法的总回报、平均回报、收敛速度及模型表现与训练步数的关系。

4 实验结果分析

实验进行了对于传统DDPG算法的实现，并在A-Speedway地图上进行了训练，训练中设置了4个约束条件，以便让小车能够正确地行驶，尽量行驶在道路中央。这4个约束条件为：1)在车辆与周边环境中的障碍物发生碰撞时，即时回报值为-50；2)在车辆行驶出当前车道时，即时回报值为-100，且有20%的概率结束此次行驶，重启TORCS客户端；3)当车辆行驶100步依然没有进展或者车辆行驶速度低于5 km/h时，结束当前回合；4)当车辆运行中车身角度处于[-90,90]以外时，结束当前回合。

在DDPG算法运行过程中发现，当车辆学习到的速度过高(超过200 km/h)，在进行转弯时会脱离轨道，对于刹车的学习不理想。长期学习不到会导致车辆一直陷于学习如何顺利度过当前弯道的情况，导致算法收敛时间变长，效率降低。因此，在进行LS-DDPG算法训练时，为了让车辆学习到更准确的驾驶技能，提高驾驶准确性和算法效率，更改了第2个限制条件来进行弯道行驶的限制，即当前车辆车身靠近车道线边缘达到阈值但未驶出车道时，返回即时回报值为-100；若车驶出了车道，则返回即时回报值为-200，并结束当前回合。同时，为消除车辆行驶速度过高这种不符合实际情况的状况，在车辆学习的后期，对于油门进行一定控制，主动刹车降低车速。

4.1 有效行驶距离

图2和图3分别为LS-DDPG和DDPG算法训练车辆在赛道上跑10圈的状况下，训练轮数和车辆每轮的行驶距离。DDPG算法下训练567轮行驶了78 102步，LS-DDPG算法训练了192轮行驶了61 942步。LS-DDPG相比DDPG算法，训练轮数上减少了375轮，效率提升了66.14%；训练步数降低了16 160步，效率提升了20.07%；LS-DDPG平均每轮行驶322步，DDPG算法平均每轮行驶138步，平均每轮行驶步数增加184步，有效行驶距离提升133%。LS-DDPG算法下车辆所学习到的策略从刚开始训练就比DDPG算法具有更长的有效行驶距离，会减少很多无效操作，提高了车辆探索的效率。后期在完成1圈的情况下，LS-DDPG算法会行驶比DDPG算法更多的步数。这是由于LS-DDPG算法在训练时有意地控制了其在训练后期的车辆速度，所以在后期LS-DDPG算法训练的车辆行驶速度没有DDPG算法高，导致同样的行驶距离下行驶步数会相对较高。

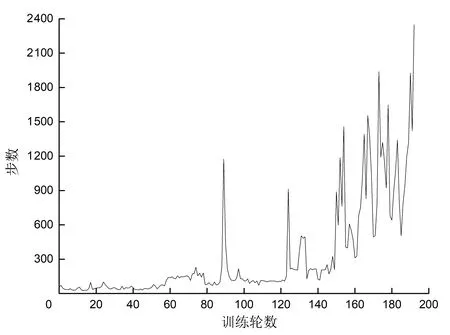
图2 LS-DDPG算法中每个回合的训练步数

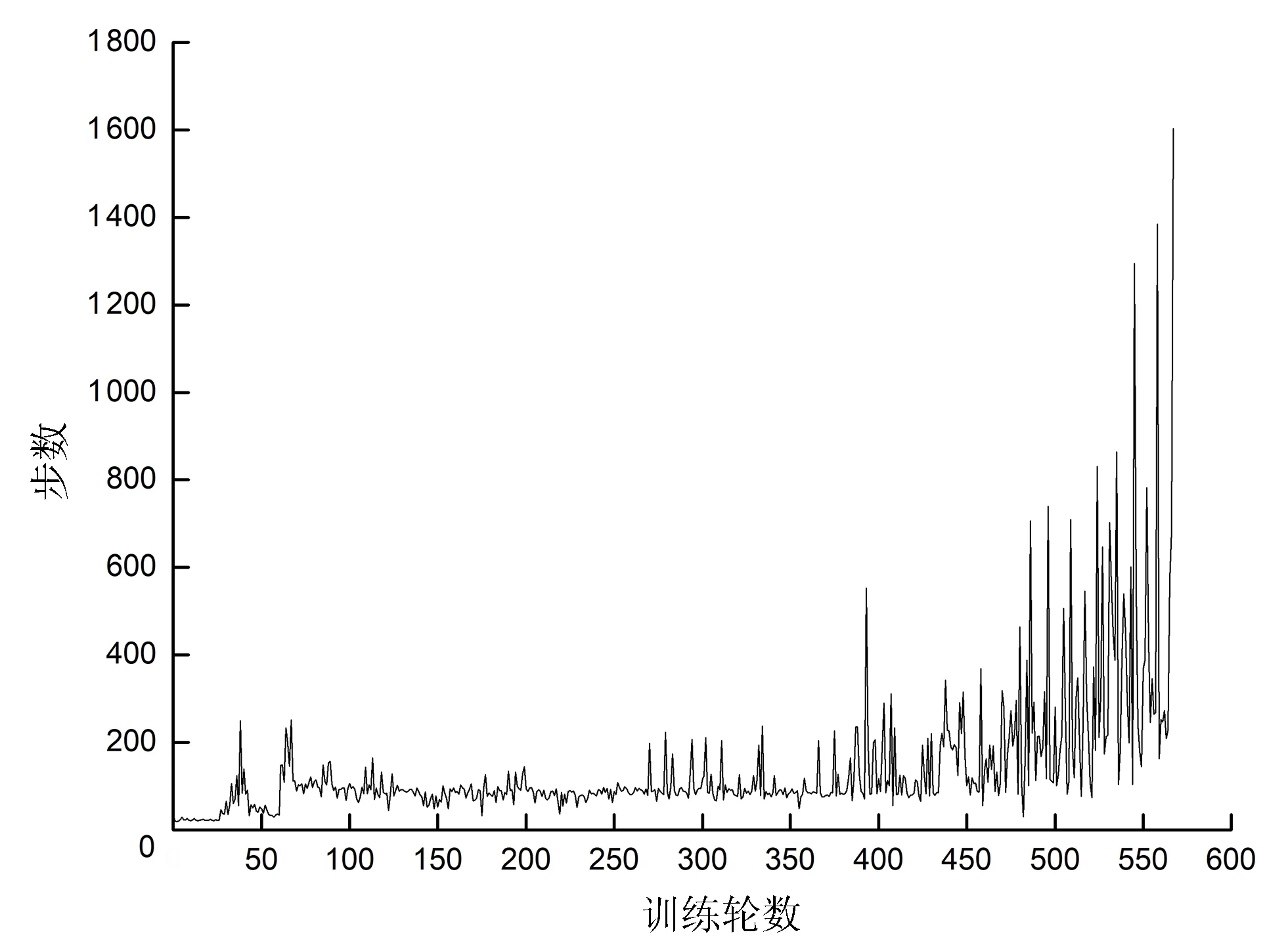
图3 DDPG算法中每个回合的行驶步数

4.2 回报值

图4和图5分别为LS-DDPG和DDPG算法在训练中对应的训练轮数和总回报的关系。LS-DDPG算法下的总回报在小范围内变动较大，在150轮后基本呈平稳上升状态。DDPG算法在400轮后呈平稳上升状态。图6和图7分别为LS-DDPG和DDPG算法在训练中对应的训练轮数和平均回报的关系。LS-DDPG算法在前期由于添加了更加严格的惩罚项,导致平均回报较小，但在120轮后会有良好的提升，后期整体处于平稳。DDPG算法在65轮后平均回报稳步上升，在训练后期平均回报高于LS-DDPG算法。由于上述提到速度控制的原因，导致LS-DDPG算法训练的车辆后期速度没有DDPG算法训练的高，回报值相比DDPG算法小。但是在行驶表现中，LS-DDPG算法训练出来的车辆在转弯时会更多地减速慢行，更符合人类的实际操控。

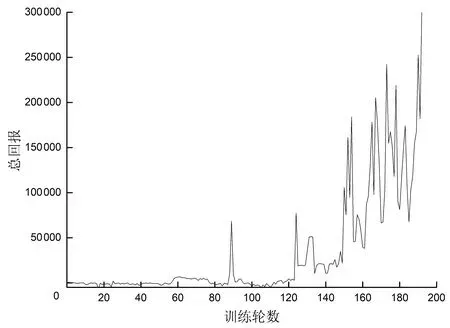
图4 LS-DDPG算法中随回合数变化的总回报值

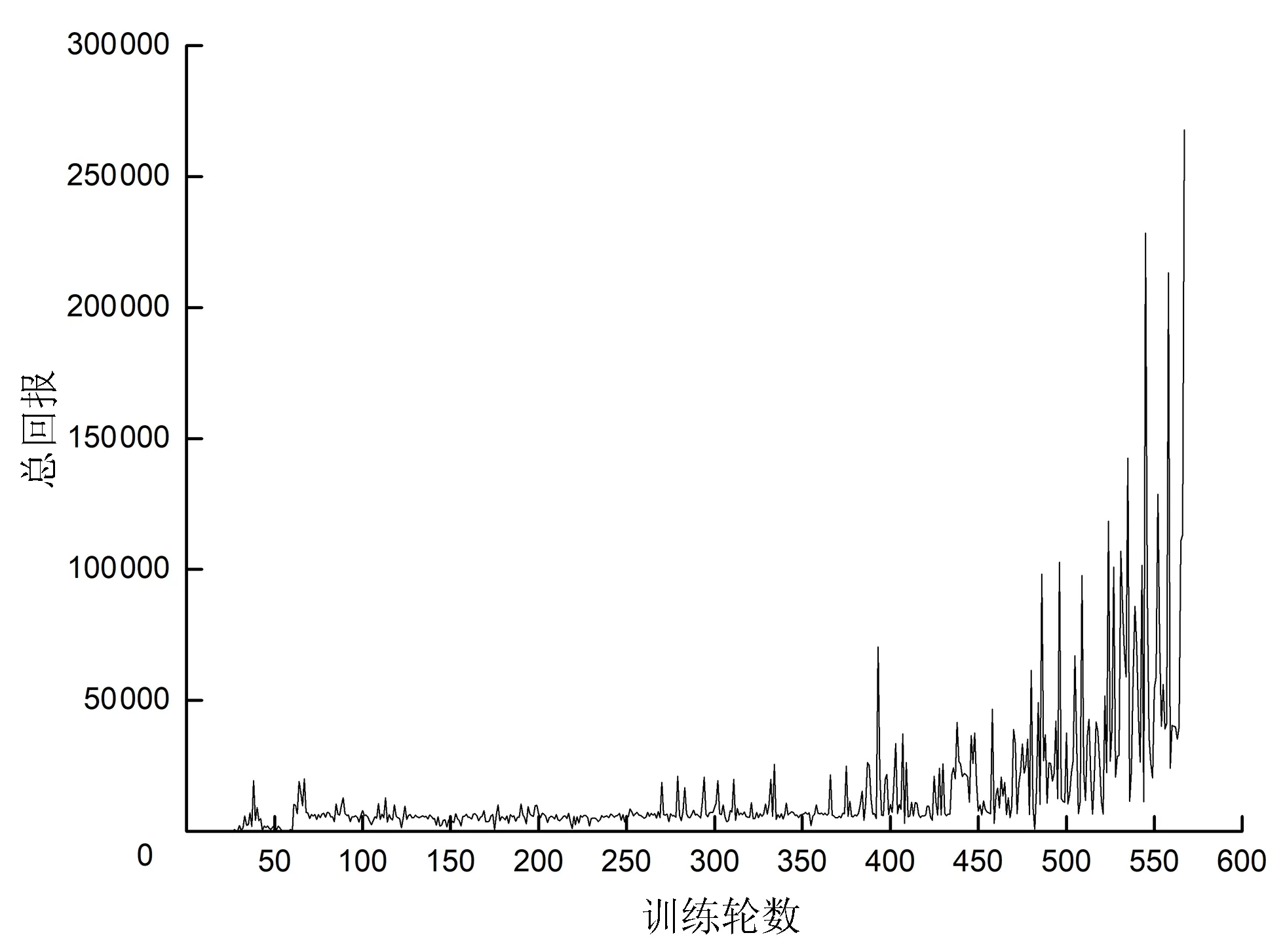
图5 DDPG算法中随回合数变化的总回报值

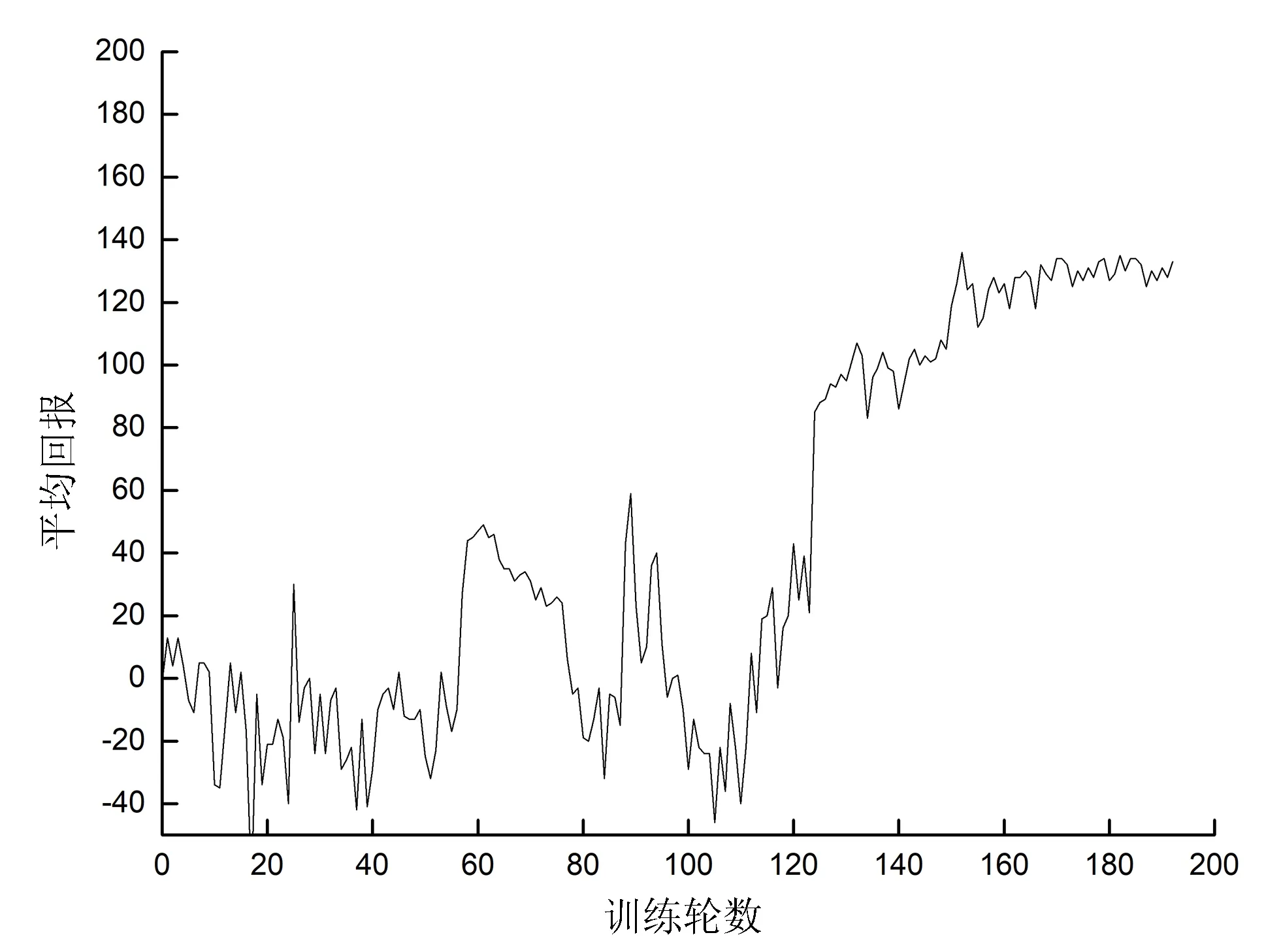
图6 LS-DDPG算法中每个回合的平均回报值

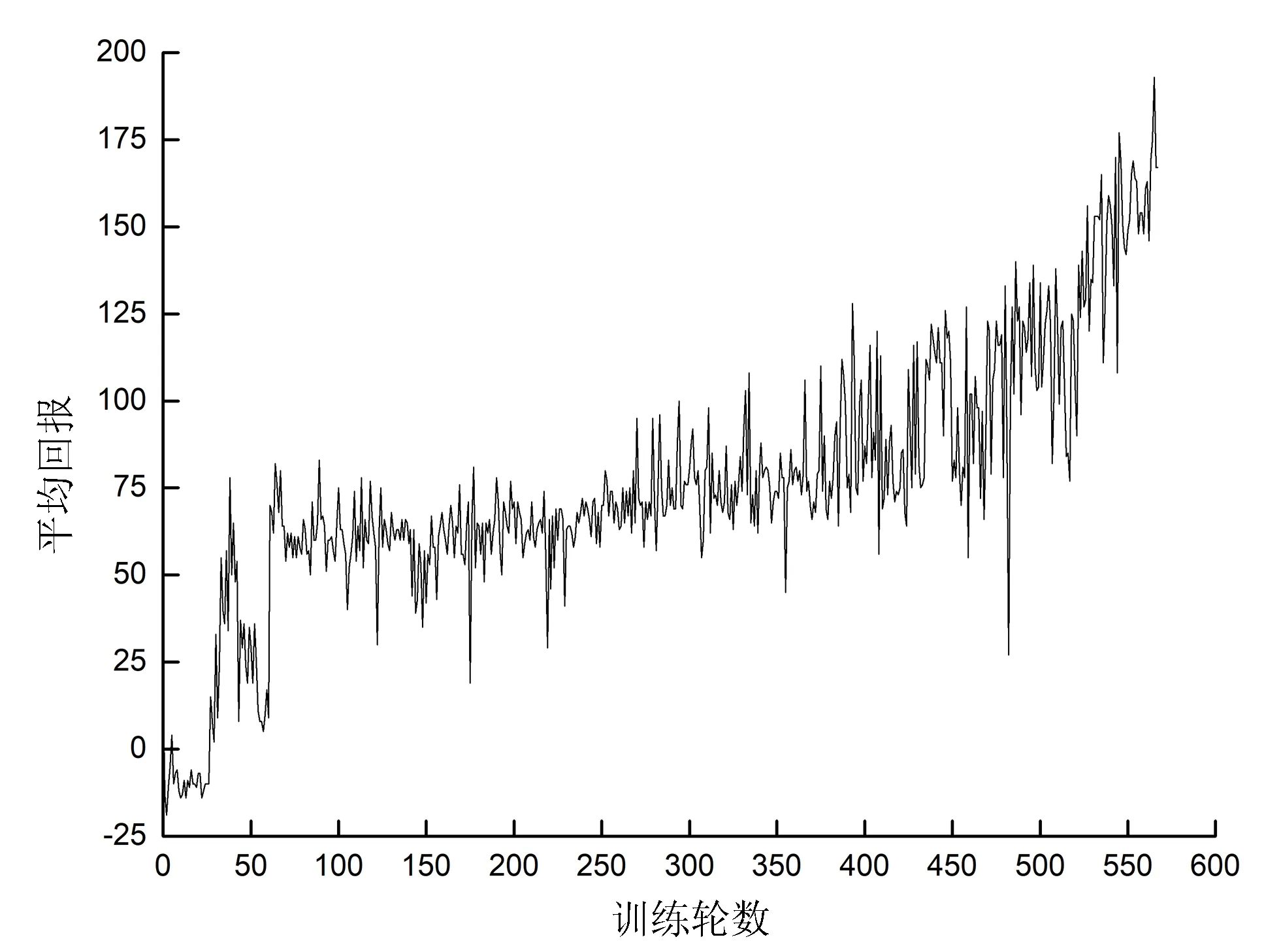
图7 DDPG算法中每个回合的平均回报值

5 结束语

分析了DDPG算法下的自动驾驶决策策略，并对传统DDPG算法进行了改进。在TORCS平台上验证了改进算法在训练效率和有效行驶距离上的提升。但该实验仅在单车辆且环境相对简单的情况下进行，缺少在复杂环境下的解决能力，且DDPG算法在高速行驶下也无法高效地学会刹车。如何根据现实情况进行更加规范的驾驶行为是下一步要研究的内容。