改进SMOTE的过采样算法

覃 琴， 杨 悦， 陈名松,3， 王 鑫,

(1.桂林电子科技大学 计算机与信息安全学院,广西 桂林 541004；2.桂林电子科技大学 北海校区,广西 北海 536000；3.桂林电子科技大学 信息与通信学院,广西 桂林 541004)

不平衡样本数据集是指数据集中某些类包含比其他类更多样本数的数据集[1]。在二分类问题中，通常将样本数较少的一类称为少数类，样本数较多的一类称为多数类[2]。在现实生活中有很多不平衡数据的分类应用场景，如信用卡欺诈检测[3]、医疗诊断[4]、网络攻击识别[5]等场景。采用传统分类算法对不平衡数据进行分类，分类结果会倾向于多数类，出现分类失误的情况[6]。这种存在于两类之间样本量的不平衡称为类间不平衡，而另一种导致分类失误的不平衡是类内不平衡[7]，指的是某类样本空间内部数据分布密度的不均衡，即形成了多个具有相同类别、不同数据分布的子类[8]。另外，过采样方法中存在合成样本重叠[9]以及样本分布“边缘化”[10]问题也是分类性能下降的原因。

对不平衡数据分类问题主要从数据处理和分类算法2个方面进行研究。分类算法的代表性算法有代价敏感学习和集成学习；数据处理最常见的方法为过采样和欠采样,分别通过增加少数类样本数和减少多数类样本数来平衡两类的样本数。相比之下，基于数据层面的采样方法简单、直观，但其中欠采样方法一般会造成信息丢失，而过采样方法则使原数据集趋于平衡，因此在数据分类领域，通常采用过采样方法。

目前最常用的过采样方法是Chawla等[11]在2002年提出的SMOTE算法，算法思路是通过寻找样本的近邻集，在样本点与其近邻集随机选择的样本连线上合成新的样本点。Han等[12]在2005年提出了Borderline-SMOTE算法，该算法将少数类样本分为边界区域、安全区域、危险区域，通过选择边界区域的样本点进行样本合成，避免了SMOTE不加区别地选择少数类样本而导致大量的冗余新样本的合成。He等[13]提出了ADASYN合成，根据数据分布自动确定每个少数类样本需要生成的样本数，近邻多数类样本多的少数类样本生成更多的样本，相比于SMOTE，对样本分布进行了细致划分。Cluster-SMOTE[14]利用K-means算法对少数类样本进行聚类，找到少数类簇，然后分别应用SMOTE算法，但该方法未确定最佳类簇个数，且未计算出每类簇该生成的样本数。Kmeans-SMOTE[15]将K-means聚类算法与SMOTE算法相结合，相比Cluster-SMOTE，Kmeans-SMOTE对整个数据集进行聚类，发现重叠的类区域且避免在不安全区域中进行过采样，并将合成样本限制在目标区域内，消除了类间和类内不平衡，同时避免了产生噪音样本，效果较好。CBSO[16]将聚类与现有的合成过采样技术的数据生成机制相结合，确保生成的合成样本始终位于少数类区域，避免了错误样本的生成。上述的过采样方法在一定程度上提高了分类精度，但仍存在以下不足：1)过采样时更多地解决类间的不平衡，而未充分考虑类内的不平衡。2)虽然通过聚类可以较好地解决类间和类内不平衡，但在聚类过程中也加剧了两类样本的混叠，导致合成新样本产生重叠样本。传统k-means聚类算法聚类时需要设置k值，算法对于球形数据集比较有效且算法复杂度较高。3)少数类边界未最大化，影响样本的合成质量。4)对合成样本不加限制目的区域，造成合成样本分布“边缘化”。5)存在噪声样本干扰问题。鉴于此，提出一种改进的过采样算法AGNES-SMOTE。

1 预备理论

1.1 SMOTE算法

SMOTE基本思想是通过人工合成新样本，以平衡原始数据中的类别失衡。SMOTE算法的步骤如下：

1)根据欧式距离计算两两样本之间的距离，对少数类数据中的每个数据样本X使用KNN算法，搜索它的K个最近邻样本。

2)对每个原始样本，随机选择其K个近邻样本中的N个样本，在原始样本数据与它的近邻样本之间进行插值操作:

xns=x+rand×(y(i)-x)，

(1)

其中：i=1,2,…,N；xns为新插值的样本；x为选择的原始样本数据；rand为0到1之间的随机数;y(i)为原始样本数据x的最近邻K个样本中选取的N个样本。

3)在原始训练数据中加入所有生成的新样本，降低训练数据集的不平衡度。

2 AGNES-SMOTE算法

2.1 划分少数类簇

AGNES-SMOTE算法首先做噪音样本处理，再采用AGNES算法对样本进行聚类，将数据集划分成类簇。AGNES是一种层次聚类算法，该算法将每个样本点看作一个类簇，然后将这些簇根据某种规则进行合并，直到达到预设类簇个数或设定的阈值。与传统质心方式聚合样本点的方法相比，AGNES算法可以不受样本点周围分布的形状限制，同时可以将特征空间范围不同的样本点聚合到一起，更好地解决类内不平衡问题。在确定类簇是否合并时，采用平均距离计算方法，直到类簇间距离超过设定的阈值，停止聚类。为了避免重叠样本的生成，还需要考虑多数类样本的分布。采用AGNES算法先对多数类样本进行聚类，再根据获得的多数类簇对少数类样本进行聚类。若某一多数类簇到两少数类簇的距离小于两少数类簇的最小距离，则表明合并后的少数类簇合成样本时会产生重叠样本，不应该将两类簇进行合并。划分少数类簇的步骤如下：

1)给定原始数据集I，利用K近邻的思想过滤数据集I中的噪声样本。设定K=5，遍历I中的样本，若I中样本的K个近邻中超过4/5的样本为该选取样本的相反样本类别，则判定该样本为噪声样本，剔除该噪声样本，将剩下的样本点组成样本集合I′。

(2)

其中：x和y分别为类簇Ca和Cb中的样本点；|Ca|和|Cb|表示类簇中总的样本数。

4)由式(2)计算两两少数簇间的距离，令Dmin=d(Ca,Cb)并记录下其最小距离对应的类簇编号a和b。

5)遍历多数类簇集合，找到多数簇Ckmaj，满足其到少数类簇Camin和Cbmin的距离均小于两少类簇最小距离Dmin，将这些多数类簇加入集合B。

6)若B≠Ø，则少数类簇Camin和Cbmin不进行合并，将最小距离Dmin设为一个较大的值，避免再次合并时被考虑，并将B中元素清空。否则，将少数类簇Camin和Cbmin合并成少数类簇Ccmin，则少数类簇集合A中将减少一个元素。

设置距离阈值Th，判断是否做类簇合并。先定义：

(3)

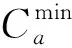
Th=davgf。

(4)

参数f用于调整聚类算法的输出。

2.2 确定采样权重和概率分布

通过AGNES聚类获得若干样本数不同的少数类簇，类簇内的密集程度也不同，需要考虑类内不平衡对分类性能的影响。于是对所有少数类簇根据样本数赋予不同权重，不仅可以保证所有的少数类簇都进行过采样，不会忽略孤立的小类簇，而且有利于避免过拟合现象。因此，根据少数类簇中样本数为其分配不同的采样权重：

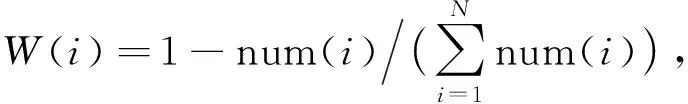
(5)

其中：N为总的少数类簇数，num(i)为第i个少数类簇包含的样本数。由式(5)可知，某少数类簇中样本数越多，在总的少数类簇中样本数和中的占比越大，则得到的W(i)越小，即分配的权重越小，合成样本数越小，最终实现同类样本之间的平衡分布。

由各类簇的采样权重W(i)和剔除噪声样本后，剩余的多数类样本与少数类样本的差额Nmaj-Nmin，可以确定每个少数类簇的采样数：

num(i)=(Nmaj-Nmin)W(i)。

(6)

此外，在分类任务中，越容易被错分的往往是越靠近决策边界的少数类样本，因而增加了少数类样本的学习难度，为此还需要筛选进行过采样的样本。这里引入少数类簇的概率分布，根据概率分布挑选难以学习的包含重要信息的少数类样本作为“种子样本”，以保证样本的合成质量，每个样本被选中的概率设置为

(7)

少数类簇的概率分布为

(8)

其中：ya为x的第a个多数类近邻样本，1≤a≤k；dxya为少数类子簇中样本x与多类样本ya的欧式距离；i为少数类簇中的某样本；n为某少数类簇中的样本数；k为近邻样本数。由式(8)可知，每个样本被选中的概率是由该样本与多数类边界的距离确定，距离多数类边界越近的少数类样本被选择的概率越大于距离较远的样本，再由每个样本被选中的概率构成少数类簇的概率分布，这样不仅考虑了样本的分布特性，而且有效地扩展了少数类决策边界。

2.3 限制合成样本的生成区域

确定了每个少数类簇合成数，并根据各少数类簇的概率分布选取“种子样本”，还需考虑合成样本的生成区域，进一步提高分类器的性能，防止合成样本分布“边缘化”。因此在进行样本合成时，需要将新生成的样本点分布考虑进去。在“种子样本”中随机选取一个样本，然后从该样本在同一少数类簇中的近邻少数类样本中再随机选择2个样本，将这3个样本组成一个三角形，样本本身作为三角形的顶点。3个顶点到其质心的连线上分别随机生成一个样本,一个三角形产生3个合成样本，采用质心方式来限制样本点的生成区域。设置3个样本点分布为x1、x2、x3。由式(9)计算出3个样本的质心：

(9)

其中：xi为3个顶点横坐标；yi为3个顶点纵坐标。按该方式生成样本点向样本点质心方向靠拢，考虑样本点分布。

2.4 算法步骤

AGNES-SMOTE算法首先采用K近邻思想对原数据集做噪音样本剔除；然后采用AGNES算法对多数类样本进行聚类，划分成若干个多数类簇；再对少数类样本进行聚类，并根据得到的多数类簇合并相近少数类簇，当超出设定阈值时停止聚类，得到少数类簇。为每个少数类簇分配权重，同时计算出每个少数类簇的概率分布，结合两者对少数类簇中的样本进行过采样,合成过程中采用质心方式对合成样本限制生成区域。具体算法如下：

1)对原始数据集进行噪音处理，将处理完噪音后的数据集分为多数类样本集和少数类样本集。采用AGNES算法对多数类样本集进行聚类，得到多数类簇，再对少数类样本集聚类，聚类过程中判断距离最近的两少数类簇间是否有多数类样本存在，再进行类簇的合并。

2)计算是少数类簇中的样本数，为少数类簇分配采样权重，计算出需要合成的样本数，再计算出每个少数类簇的概率分布。

3)通过每个少数类簇需要合成的样本数和概率分布选取“种子样本”,在所有“种子样本”中选取一样本，再随机选取该样本所在类簇的2个近邻少数类样本,将3个样本组成一个三角形，在3个样本点到其质心的连线上合成新样本，再将合成样本添加到合成样本集中。

3 实验设计与结果分析

3.1 评价指标

传统分类算法采用混淆矩阵[17]来进行评价，如表1所示。

表1 混淆矩阵

分类器进行分类采用准确率(Precision)和召回率(Recall)两个基础指标[18]，分别定义如下：

Precision=TP/(TP+FP)；

(10)

Recall=TP/(TP+FN)。

(11)

在不平衡数据的处理中，一般采用常用F-measure、G-mean和AUC这3个指标来评价分类算法的优劣。其中F-measure是召回率和准确率的调和平均数，实验中将β设置为1[19]。G-mean则结合了分类器在多数类样本和少数类样本上准确性，AUC表示ROC曲线下各部分的面积之和。F-measure和G-mean定义如下[20]：

(12)

(13)

3.2 实验分析

3.2.1 数据集

选取6组UCI数据集进行实验，数据表结构如表2所示。

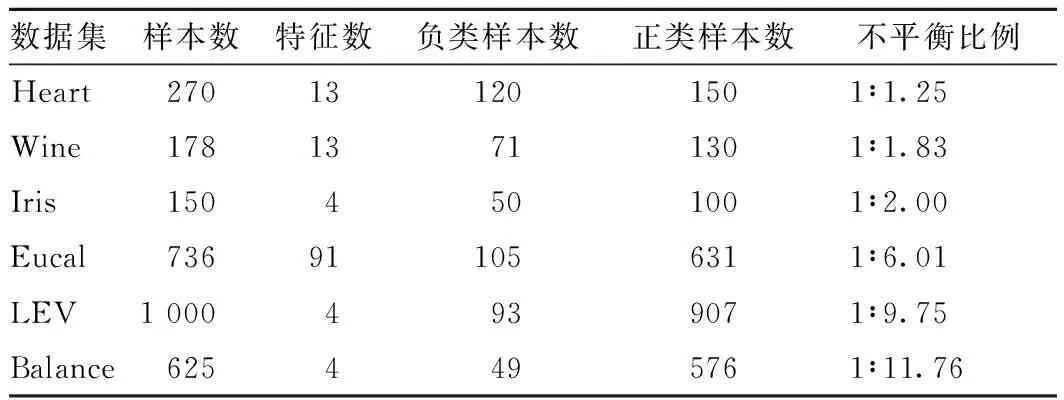
表2 不平衡数据

3.2.2 确定参数f

将6组数据集作为测试数据集，确定参数f的范围，如表3所示。对于f，以0.2为初始值，步长为0.2，进行实验。经过测试，分别有1组数据集在f取0.4时取得最大F-measure值，3组数据集在f取0.6时取得最大F-measure值，2组数据集在f取0.8时取得最大F-measure值，所以参数f的参考范围为0.2～0.8。

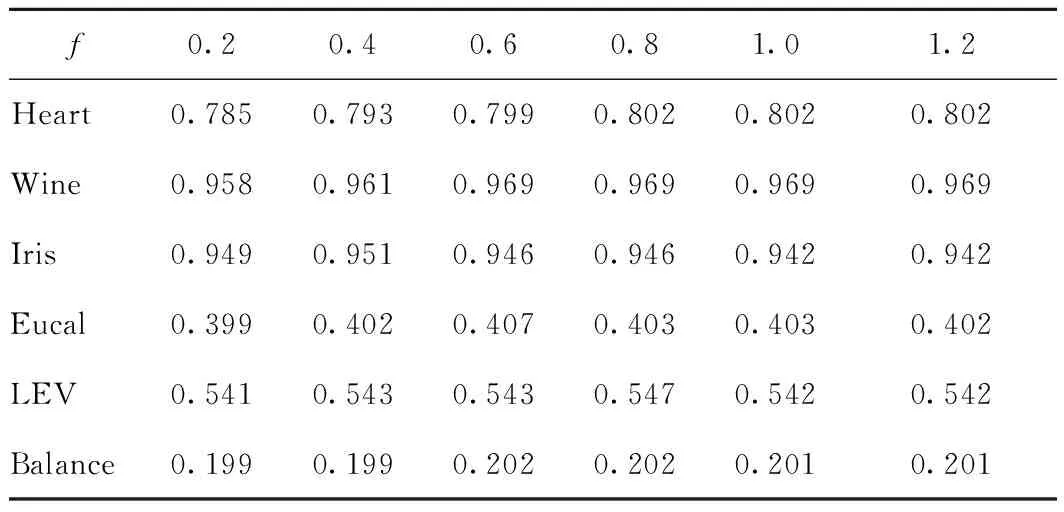
表3 不同f值下的F-measure值

3.2.3 实验结果与分析

分别用SVM、KNN和逻辑回归分类器对采样后的数据集进行分类，各分类器实验结果如表4、5、6所示。通过对比数据可得到如下结论。

表4 SVM分类器实验结果

表5 KNN分类器实验结果

表6 逻辑回归分类器实验结果

1)在处理相同数据集过程中，用SVM分类器取得的分类结果优于KNN和逻辑回归分类器。这是因为SVM的最终决策函数只由少数的支持向量确定，这不但可以抓住关键样本、“剔除”大量冗余样本,而且该方法既算法简单,又具有较好的“鲁棒”性。

2)用过采样算法对数据进行处理可以提高分类器对数据集的分类性能。将本算法与SMOTE、Kmeans-SMOTE、Cluster-SMOTE进行对比实验。从实验结果可看出，AGNES-SMOTE算法在数据集Heart、Wine、Iris和LEV上得到的AUC值、F-measure值和G-mean值大部分优于其他采样算法。原因是本算法在SMOTE算法及其改进算法存在的不足上做了改进，在不平衡数据处理上，不仅考虑了类内不平衡，而且对样本加以选择的同时限制了样本的生成区域，减少了样本重叠的可能，进一步保证了样本的合成质量，为分类器提供了多样的样本信息。

3)在数据集中，AGNES-SMOTE算法处理不平衡比例较小及特征数较少的数据集时表现效果较好。在数据集Heart、Wine和Iris上取得了较高的AUC值、F-measure值和G-mean值，而在数据集Eucal、LEV和Balance上取得的值相对较低，这是因为数据集的不平衡比例增大且其中数据集Eucal包含较多的特征数，使得数据结构表现较为复杂，过采样算法处理这一类型数据集时产生干扰，因而对分类器分类性能的提升较差。而对于不平衡比例较大的数据集，AGNES-SMOTE算法相比其他采样算法依然能取得较好的AUC值、F-measure值和G-mean值。

因此，AGNES-SMOTE算法在不平衡数据处理上，降低了噪音干扰，减少了合成重叠样本，对容易错分的边缘样本加以选择，考虑了类内不平衡及生成样本点的分布，提升了分类性能。

4 结束语

针对不平衡数据集分类问题，现有的过采样算法更多地解决类间不平衡，而未考虑少数类类内不平衡，未筛选进行过采样的样本以及去除噪音，合成过程中存在样本重叠以及样本分布“边缘化”的问题，提出了一种基于层次聚类和改进SMOTE的过采样方法AGNES-SMOTE。该算法首先对数据集过滤噪音样本，使用AGNES算法分别对多数类和少数类样本进行聚类，根据得到的多数类簇划分少数类簇；其次，根据少数类簇的采样权重和概率分布挑选进行过采样的样本；最后，采用质心方式来限制合成样本点的生成区域。AGNES-SMOTE对数据集处理过后，结合分类器在UCI数据集上与其他算法进行对比实验，实验结果表明，选用SVM分类器可以更好地提高少数类样本的分类准确度和整体分类性能。该过采样方法只针对于二分类数据，而实际中的数据大多属于多类别数据。下一步将研究针对多类别数据的分类算法，进一步优化模型。