基于小波包熵及双重优化神经网络的牵引逆变器开路故障诊断

2022-05-17赵苗苗陈小强王英贺彦强

铁道科学与工程学报 2022年4期

赵苗苗，陈小强,2，王英,2，贺彦强

(1.兰州交通大学自动化与电气工程学院，甘肃兰州 730070；2.光电技术与智能控制教育部重点实验室，甘肃兰州 730070)

伴随我国轨道交通的逐渐发展，高速铁路成为铁路发展的重要趋势[1]。高速动车组(Electric Multiple Units，EMUs)作为高速铁路不可或缺的执行单元，其安全性和可靠性关系到整个高速铁路的行车安全[2]。电力牵引传动系统为EMUs提供原动力，所受负载突变、电磁干扰、自身老化等不确定因素影响较大，运行环境复杂，使得牵引变流器的功率模块器件(IGBT)极易发生故障[3]，据工业调查显示，该部件故障率达60%以上[4]。因此，及时诊断和定位牵引变流器故障点是保障牵引传动系统安全可靠运行的必要前提。IGBT的开路和短路故障是牵引变流器最主要的2种故障类型。对于IGBT短路故障，现有的IGBT模块驱动电路已经集成了较完备的短路故障检测和硬件保护装置[5]。而IGBT的开路故障由于长时间开路引起网侧电流和直流侧电压波动增大，导致牵引电机异常运行[6]，引发其他关联器件的二次故障。目前牵引变流器功率模块器件IGBT的开路故障诊断技术主要有3种方法[7]：基于模型解析的诊断方法，通过建立系统动态解析模型得到先验信号与系统实际测量信号比较构建残差信号，设定阈值并与残差信号对比确定故障点。有混杂模型[8]、状态观测器[9]、滑模观测器[10]、键合图模型[11]、等价空间和滤波器[12]等。基于信号处理的诊断方法通过分析系统所测信号的幅值、相位、谐波等信息提取故障特征，检测故障位置[13]。故障特征提取方法主要有傅里叶分解、小波(包)变换[14]、经验模态分解[15]和谱峭度[16]等。基于信号处理方法诊断耗时久且易受系统噪声和负载扰动的影响；基于知识的故障诊断方法不需要建立准确的数学模型，但大量的计算导致诊断速度依旧较慢，常见的方法有神经网络[17]、模糊算法以及小波神经网络[18]等。三电平牵引逆变器相比两电平牵引逆变器降低了开关频率，承受电压高，但故障种类冗杂。因此，针对三电平牵引逆变器，提出一种小波包熵结合双重优化神经网络的牵引逆变器开路故障诊断方法。采用PSO算法和GA同时对神经网络权值和阈值进行优化，得到满足条件的最优权、阈值训练和预测网络，提高了故障诊断的可靠性，结合小波包熵提取特征数据可以精确定位故障功率管。

1 牵引逆变器故障工作模式分析

1.1 三电平牵引逆变器拓扑结构

以CRH2型动车组为例，其牵引传动系统框图如图1所示，该列车有2个动力(供电)单元，牵引变流器包含脉冲整流器、中间直流回路和三电平牵引逆变器。该三电平牵引逆变器是电压源型逆变器，在牵引工况下逆变得到三相交流电供给牵引电机，再生制动工况下整流得到直流电，输送到整流器反馈给牵引供电网，主电路如图2所示。图中，ud是直流侧电压，C1，C2为支撑电容，iN为逆变器输出侧三相相电流。

图1 CRH2型动车组牵引传动系统框图Fig.1 Block diagram of traction drive system of CRH2 EMU

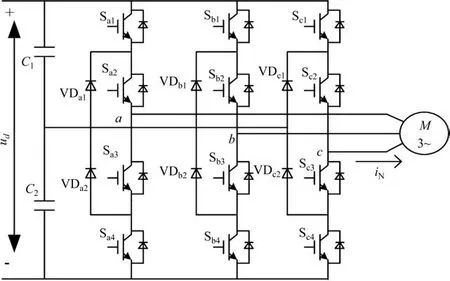
图2 三电平牵引逆变器主电路原理Fig.2 Schematic of the main circuit of the three-level inverter

1.2 三电平牵引逆变器开路故障分析

实际运行中牵引逆变单元发生故障情况多为1个或2个IGBT开路故障，3个及以上功率管故障的现象极少，但三电平逆变器有12个功率管，故对于多管故障的诊断也不容忽视。

以图2三电平牵引逆变器主电路图为例分析，对于开关管IGBT开路故障分类如下：

1)单独1个开关管发生开路故障，共12种模式，例：Sa1和Sa2等。

2)单相桥臂上、下半桥各有1个开关管发生开路故障，共12种模式，例：Sa1和Sa3，Sa2和Sa3等；单相桥臂上半桥或下半桥2个开关管发生开路故障，共6种模式，例：Sa1和Sa2，Sa3和Sa4等；不同两桥臂2个开关管开路故障，有48种模式，例：Sa2和Sb1，Sa1和Sc1等。

3)不同桥臂3个开关管故障，有64种模式，例：Sa1，Sb1和Sc1等；不同两桥臂分别1个、2个开关管开路故障，共144种模式，例：Sa1，Sb1和Sb2等。

根据三电平牵引逆变器三相对称，以A相单管开路故障为例，正常工作模式和故障模式下电流iN流向如图3所示，通过图3可以发现开关管IGBT发生故障会引起牵引逆变器运行拓扑结构发生变化，从而导致牵引逆变器输出侧三相电流iN波形特征发生变化。图4为三电平牵引逆变器A相上桥臂单管故障仿真波形，分析不同故障模式下iN波动情况，得到故障情况下电流特征变化：单管Sa1开路故障时A相电流正半轴幅值减小，Sa2开路故障时A相电流正半轴幅值为0；Sa3开路故障时A相电流负半轴幅值为0，Sa4开路故障时A相电流负半轴幅值减小。多管故障的电流幅值变化是单管故障下电流特征量的叠加，且电流幅值特征遇零为零。故本文选取三电平牵引逆变器输出侧三相相电流iN作为故障特征量。

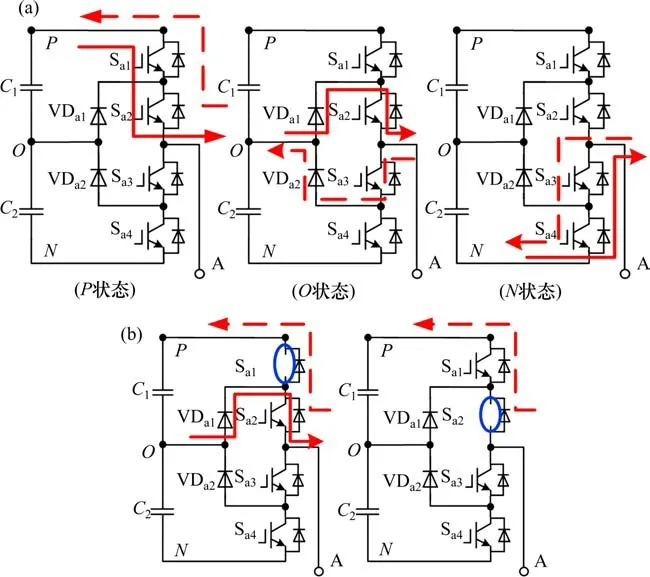
图3 正常和故障模式下逆变器电流i N流向对比Fig.3 Comparison of inverter current i N flow in normal and fault modes

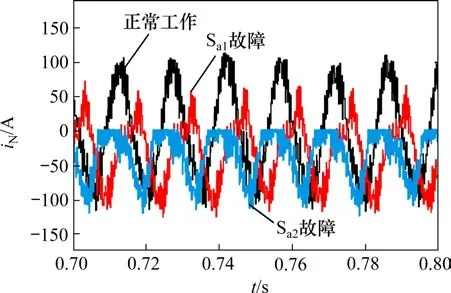
图4 A相上桥臂单管故障仿真电流波形Fig.4 A-phase upper arm single tube fault simulation current waveform

2 故障特征提取

2.1 小波包信号分解

提取正常模式和故障模式下逆变器输出侧电流iN，根据实际需要，本文对三电平牵引逆变器输出侧电流信号进行3层小波包分解，分解示意图如图5所示。图5中，pij的位置是第j层上的第i个节点，记为节点(j,i)，其中p10是原始信号。

图5 3层小波包分解示意图Fig.5 Schematic diagram of 3-layer wavelet packet decomposition

小波包算法包括分解算法和重构算法。小波包分解算法递推公式为：

其中：f(t)是原始时间信号；G，H为小波分解滤波器；t为离散时间序列，t=1,2,…,N；j=1,2,…,J；i=1,2,…,2j；J=log2N。小波包重构算法递推公式为：

其中：j=J-1,J-2,…,1,0；J=log2N；i=2j,2j-1,…,2,1；h,g为小波重构滤波器，在1 s时触发Sa2开路故障，以小波分解第3层第1个节点为例，一个周期采样400个点，设置3个周期后触发故障，故障相电流变化及分解系数如图6所示。通过图6可知故障电流比正常电流具有更多的频率分量。

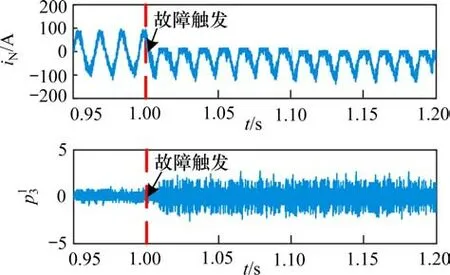
图6 A相电流波形和小波包分解系数Fig.6 A phase current waveform and wavelet packagedecomposition coefficient

2.2 能量熵信号提取

对信号f(t)进行3层小波包分解，所得8个频率段进行重构，重构后的序列表示为Sj(i)。引入滑动时间窗为Cn(Pn(δ),ω,δ)，其中Pn(δ)=1+nδ为时间窗的初始位置，n为初始信号步数，ω=1,2,…,N为窗宽因子，δ=1,2,…,N为滑动步长。因此尺度j下信号对应时间窗Cn内第i点的能量可以表示为：

在尺度j下对应时间窗Cn内总能量表示为：

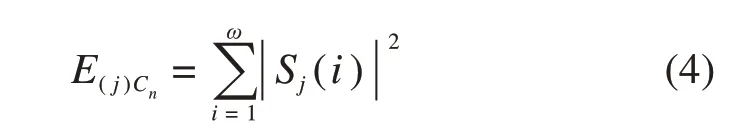
时间窗内的相对小波包能量为：

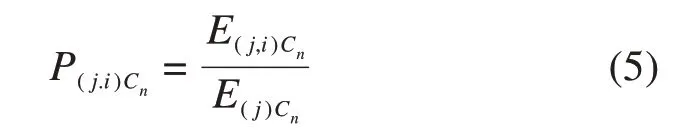
与此对应的小波包熵为：

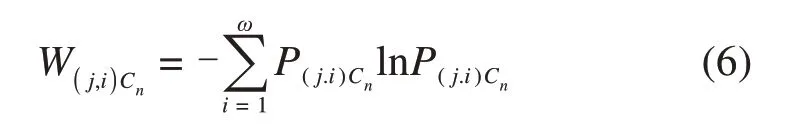
以Sa2故障为例，在1 s时触发故障，故障前后熵值对比如图7所示。可以看出，故障模式下三相电流的熵值远大于正常模式下的熵值，故障特征更明显。三电平逆变器发生故障后，其故障电流通过小波包分解，故障信息存储在子频带中，对小波包3层分解所得14个节点根据式(6)进行熵值计算，获得14维故障特征向量作为故障诊断检测数据。

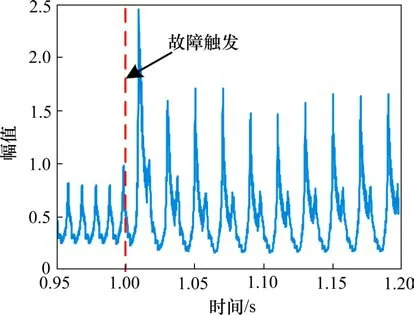
图7 Sa2故障前后小波包熵变化Fig.7 Wavelet entropy changes of Sa2 before and after fault

3 双重优化BP神经网络

BP神经网络对故障诊断拟合能力较高，但网络预测结果中某些样本点的预测误差较大。且在逼近任意非线性映射关系的过程中，容易陷入某些局部最小值，这种情况下，系统的误差不会减小，诊断时间则更长。因此提出PSO结合GA优化神经网络权值ωij，ωjk和阈值xi,aj,bk的更新。使2种算法优劣互补，PSO-GA优化的BP神经网络算法流程框图如图8所示。

图8 PSO-GA优化的BP神经网络算法流程图Fig.8 PSO-GA optimized BPneural network algorithm process block diagram

4 实验验证

搭建三电平牵引逆变器的仿真模型，选取直流侧电压ud为2 600 V，支撑电容为2.125 mF，验证所使用BP神经网络的正确性[17]。选取三电平逆变器典型的11种故障模式输出侧电流信号经过3层小波包分解所得节点的小波包熵值作为神经网络的输入数据，样本总数为11×14=154组故障数据。根据样本数据确定BP神经网络输入层节点q=14，输出层节点m=11，隐含层节点l根据式(7)确定大致范围，式(7)中，a为0～15之间的常数。分类误差同隐含层节点数关系见图9，选取隐含层节点数l=28。

图9 预测误差和隐含层节点数关系Fig.9 Predicting error and hidden layer node relationship

BP神经网络是14×28×11的结构，神经网络传递函数均采用Sigmoid函数，训练方法采用反向传播的LM算法，减少算法运行计算量。实验过程中，将154组数据样本分为2部分，选取98组采样数据作为BP神经网络的训练数据，剩余数据为测试数据。PSO-GA优化算法种群粒子数c为154，每个粒子的维数d为2，迭代进化次数为200次，经过多次试验，选取PSO-GA优化算法的适应度阈值为0.1，BP神经网络误差阈值为0.01。

在相同的样本数据情况下，本文所提出PSOGA优化BP神经网络方法与BP神经网络、GA优化BP，PSO优化BP算法迭代200次的误差损失率和故障识别误差对比分别如图10和图11所示。由图10和图11可知，PSO-GA-BP算法对于三电平牵引逆变器故障诊断，误差率随迭代次数下降速度明显比其他3种快，相同情况下，误差最小，故障诊断精确度最高。

图10 4种方法的迭代损失率对比Fig.10 Comparison of the iterative loss rate of the four methods

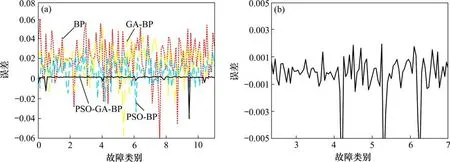
图11 故障识别误差对比Fig.11 Comparison of fault recognition errors

5 实用性分析

5.1 抗干扰性

实际铁路运行中噪声不可避免，为研究该诊断方法对铁路沿线噪声的抗干扰性，以Sa2故障为例，对故障相网侧电流iN加入信噪比(SNR)为5 dB的高斯白噪声，噪声对故障模式下小波包熵的影响如图12所示。

图12 噪声对小波包熵影响对比Fig.12 Comparison of the influence of noise on wavelet packet entropy

图12表明，噪声会对三电平逆变器故障成分的提取造成干扰，为验证噪声对本文所提出检测方法的影响，引入相似度函数表征噪声对小波包熵的影响程度，定义如下：

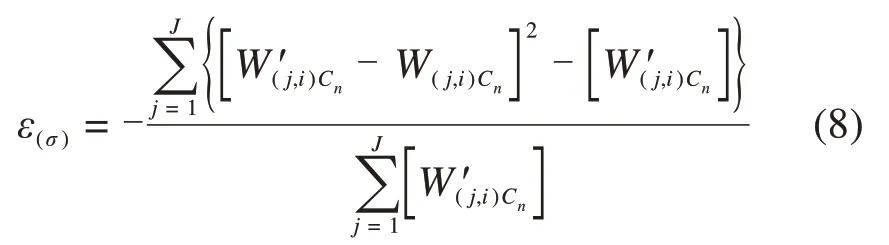
其中：σ为信噪比大小；W(j,i)Cn为原始故障信号的熵值，W′(j,i)Cn为故障信号加噪后的熵值，相似度值ε∈[0,1]，相似度值越大，噪声对信号的影响程度越小。对故障信号加入0～30 dB的高斯白噪声，绘制相似度函数曲线，如图13所示。根据信噪比在0～30 dB范围内的相似度值可知，所使用的小波包熵具有一定抗噪能力，只有当噪声值极大时才会影响故障信号熵值的分布。

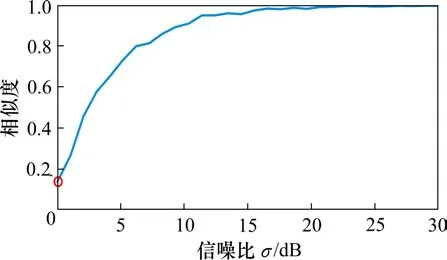
图13 相似度函数曲线Fig.13 Similarity function curve

根据我国铁路环境噪声边界限值[19]可知，铁路沿线边界噪声限值在昼间和夜间均为70 dB，因此本文提出的诊断方法在实际运行中能满足抗噪性需求，不需要额外对信号进行降噪处理。

5.2 实时性

本实验使用CPU型号为Inter(R)Core(TM)i5-8250U，主频1.80 GHz，内存8 GB，GPU为Rade‐on(TM)540的计算机中的Matlab 2018软件平台进行仿真。表1是本文提出诊断方法与已有文献诊断方法时间性能比较，测试进行多次重复验证，取其平均值作为最终标准。可以看出，PSO-GA-BP诊断算法在迭代次数、诊断准确率方面均优于其他3种算法，由于算法的复杂度提高，诊断时间没有显著减少，但该时长在器件保护动作时间范围之内，实时性高。