量纲分析与工程数据挖掘结合的掘进总载荷建模

张丽婷，张茜，周思阳，刘尚林

(天津大学 机械学院，天津 300350)

目前，越来越多的工程装备可以持续不断地从遥感、过程监测和环境检测中获得丰富的实时施工数据[1]，其中包含大量潜在知识信息。工程问题影响因素多且复杂，其监测数据往往具有高维、参量间相互耦合等特征，如何提取其中蕴含的参量间影响规律，建立关键性能参数的预估模型，是近年来工程装备智能控制与决策研究的热点问题之一。全断面隧道掘进机是一类广泛用于地铁隧道施工的重型装备，地下环境复杂多变，其安全高效掘进对参数合理调控提出很高的要求。随着掘进实时监测数据日益丰富，国内外学者开展了大量掘进工程数据分析建模的相关研究。早期，很多研究者基于工程数据的统计分析建立了掘进性能经验模型[2-3]，但这类回归建模中参量之间非线性关系的确定是难点，往往通过比较其不同初等函数的相关性来分析确定，导致对参量间物理制约关系描述不足。随着信息领域机器学习技术的迅速发展，为挖掘数据中参量间耦合关系，建立反映其非线性映射关系的模型提供了丰富的工具。部分研究者开始应用机器学习算法进行掘进性能的预测建模，MAHDEVARI等[4]应用支持向量机通过多个岩石及操作参数对掘进速率进行预测建模并与多元线性回归方法对比，结果表明该算法具有较好的预测精度；GHASEMI等[5]基于岩石单轴抗压强度、脆性指数等4项主要影响参量，应用模糊逻辑算法建立了掘进速率预测模型；LI等[6]应用长-短期记忆网络算法，利用上升阶段30 s的数据预测稳态阶段的总推力和刀盘扭矩。上述工作将不同智能算法引入掘进性能参数建模，考虑多因素对目标量的综合影响以及影响因素间的非线性关系，对于测试数据集具有很好的预测准确度。然而，目前基于机器学习进行的工程数据建模基本上还属于“端到端”的黑箱型训练，对因果关系的描述及其可解释性不显著；同时，由于缺乏内在机理的理性指导，难以充分挖掘和描述数据中的共性规律，基于特定工程训练的模型，往往仅适用于少数相似情况，其泛化能力仍有待进一步探究[7-8]。目前已经有越来越多的学者指出人工智能需要数据驱动与知识驱动相结合[9]。因此，针对掘进性能这类包含物理属性的建模问题，若能够将其物理先验知识与数据机器学习有效结合，将有利于提高模型的可解释性和泛化性，也是推进装备智能化的重要基础。然而，由于掘进工程问题的复杂性，如何获取恰当形式的物理先验知识并能够与数据挖掘过程结合是实现上述目标的关键和难点。本文针对隧道掘进装备的核心控制参数掘进总载荷，提出一种量纲分析与工程数据挖掘相结合的参数建模方法。该方法对反映参量本质物理属性的量纲进行分析，获得参量间的物理制约关系得到无量纲模型框架，并将其输入工程数据挖掘算法约束模型训练过程，建立具有一定物理可解释性的定量预估模型。为进一步验证模型的泛化性和方法的有效性，基于该方法分别建立适用于土、岩2类典型地质工况的掘进总载荷预估模型，并将其用于我国4个实际工程案例进行计算与分析。通过在独立测试数据集上进行预测评估，讨论模型的泛化性和方法的有效性。

1 量纲分析与工程数据挖掘相结合的掘进总载荷建模方法

掘进机的驱动总载荷主要包括总推力和总扭矩。施工过程中，设备在总推力作用下不断克服阻力向前推进，安装在刀盘上的刀具贯入地层，在总扭矩作用下维持刀盘旋转，切削挖掘岩土地质。装备与地质间的相互作用是影响掘进载荷的决定性因素。由于不同地质类型的性能参数、匹配装备和破坏机理有所差异，故掘进载荷的影响关系难以用统一的模型涵盖。已有研究表明，在地质参数和装备类型相似的情况下，掘进性能随影响参量变化呈现相近的规律[10]。因此，本文基于地质与匹配装备类型研究隧道工程中土、岩2种典型工况下的载荷模型。

掘进载荷受到结构、操作和地质等多方面因素的影响，是典型的多参量耦合问题，要建立具有物理含义的先验知识模型，难以从理论推导的角度进行分析。基于量纲分析的建模可直接从反映其根本物理含义的基本量纲角度对众多物理参量进行分析，获得包含一定物理机理且量纲平齐的参数模型，使得建立具有一定可解释性和泛化性的载荷模型成为可能。此外，为了获得更利于实际施工应用的显式可解释模型，本文应用一种机器学习回归算法对模型进行训练。

首先，针对不同地质工况分别分析确定地质、操作和装备结构3类影响因素中对掘进载荷产生显著影响的主要参量；然后，基于量纲分析П定理的基本思想并结合地质破坏特征分析计算各主要参量间的物理制约关系，搭建适用于此类工况的掘进载荷模型框架，为获得包含一定物理机理和可解释性的机器学习模型奠定基础；最后，结合具体工程数据将已搭建的模型框架作为输入，采用适用于掘进数据统计特征的Lasso(Least Abso‐lute Shrinkage and Selection Operator)算法识别训练，提取个体工况特征，实现掘进载荷定量建模。通过力学、量纲分析与工程数据挖掘相结合，兼顾建模的可解释性、泛化性与准确性，建模流程见图1。

图1 量纲分析与数据挖掘相结合的参数建模方法Fig.1 A parametric modeling method combining dimensional analysis and data mining

2 基于量纲分析的掘进总载荷建模

参量的量纲能够反映其本质物理属性，量纲关系包含了潜在物理规律。本文从各参量的量纲出发进行分析建模，依据量纲分析П定理[11]的基本思想，任何一个物理关系均可由该关系中物理参量间构成的无量纲量表示出来，掘进载荷与各参量之间具有如下关系：

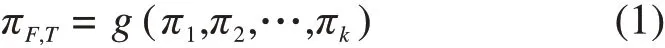
其中：k=(n-3)，n为不同工况中的影响参量个数，π1,π2,…,πk,πF,T为由各影响参量构成的无量纲π量。

为了构建式(1)所述无量纲π量，需要从各影响参量中筛选出反映掘进载荷影响关系的本质核心参量作为基本量对各物理参量进行无量纲运算，本文主要通过2个步骤进行分析和计算：基本量选择和π量构建。其中π量是指各影响参量基于基本量无量纲运算后的参量。

2.1 基本量选择

基本量的选择直接影响参量间的函数关系，然而其选择方法具有一定自由性，需要结合具体问题的特征加以确定，以获得能够反映问题潜在物理规律的参数模型。筛选流程如下：首先，确定需要分析的n个影响参量，由于基本量个数应当与研究问题的基本量纲数相等，故将其按基本量纲分为r组；然后，从每组中选出一个参量作为基本量，例如在力学系统中基本量纲有3个：质量量纲M，长度量纲L和时间量纲T，即分为3组；最后，基于已选基本量对剩余影响参量做无量纲运算，构造m(m=n-r)个π量。

对于基本量的选取，主要从3个方面综合考虑：1)对目标量有关键影响的常数参量优先考虑作为基本量。这是因为通过数据分析探究参量间物理规律时，常数参量往往难以体现其影响，引起分析盲区。2)构建π量本质上是将基本量作为单位系统来度量各参量[12]，即度量方式的切换。分析发现，选择量纲相对简洁的基本量利于获得更多特征信息。因此，从“度量标尺”的角度考虑，应选择量纲相对“简洁”的影响参量。3)结合具体问题依据各参量与目标量的影响关系进一步分析选择基本参量。此外，基本量量纲之间应相互独立。隧道掘进状态主要受到设备尺寸、施工操作和地质条件三方面因素的影响。通过对掘进过程中装备与周围地质间相互作用特点的分析，并结合实际工程经验，选取如下对掘进载荷影响比较显著的参量进行分析与建模。其中，刀盘直径是装备结构尺寸的关键影响参量；在操作参数中，与掘进载荷直接相关且影响较大的主要为掘进速度、刀盘转速和密封舱压力；对于地质参数，分析发现众多地质参数间存在较大的相关性，比如岩石节理、完整性系数等对掘进载荷的影响可以包含在剪切模量、地质密度等核心参数中，因此主要考虑剪切模量、地质密度、泊松比等基本参量来反映地质特征。各工况的具体参量及其量纲见表1，遵从量纲简洁的原则，对于基本量纲M，选择地质密度ρ作为基本量；对于基本量纲L，有刀盘直径D和隧道埋深H可选，由于刀盘直径是对掘进总载荷有直接影响的常数参量，故选其作为基本量；对于基本量纲T，选择刀盘转速ω作为基本量。综上，将地质密度ρ，刀盘直径D和刀盘转速ω作为基本量选取的方案之一。

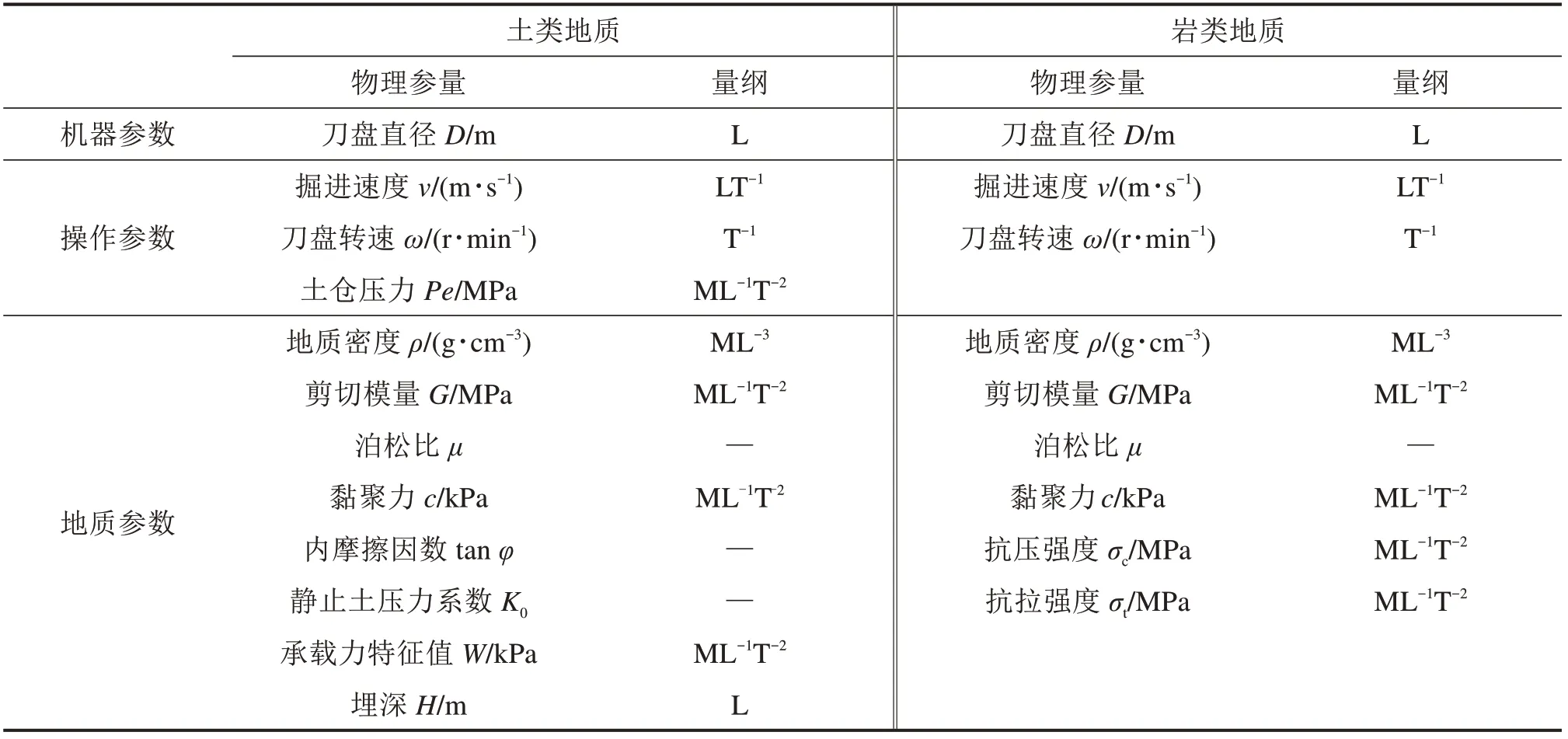
表1 各工况的具体影响参量及其量纲Table 1 Influence parameters and dimensions of each working condition

进一步结合具体问题进行分析。当装备在土类地质中掘进时，土体主要发生剪切破坏，其密度是直接影响土体抗剪强度等多项物理性能的关键参数。土体密度首先决定了土粒间空隙和咬合力的大小，进而影响其内聚力、抗剪强度等。因此，地质密度ρ是一项关键影响参量，将其作为基本量符合力学原理。但岩类地质和土类地质不同，岩体的破坏强度等物理性能不仅受到密度的影响，岩体成分类型是更为关键的影响因素。因此，对于岩类工况而言，依旧将地质密度选为基本量不够合理。当掘进机在岩类地质中掘进时，刀盘破岩过程中滚刀滚动轨迹下方的压碎区周围会产生很多横向裂纹，进而裂纹扩展、贯通，最终岩石剥落，而这些横向裂纹的产生和扩展与剪切破坏紧密相关[13]。因此，对于岩类地质，将剪切模量G替换ρ作为基本量。基于上述分析，获得了2组基本量，土类地质：ρ,D,ω；岩类地质：G,D,ω。

2.2 π量构建

基于已选基本量，通过矩阵运算构建π量。各工况自变量xi和目标量y可由基本量纲M,L和T表示为式(2)所示形式，其中αi,βi,γi为参量xi的基本量纲指数，α,β,γ为目标y的基本量纲指数。

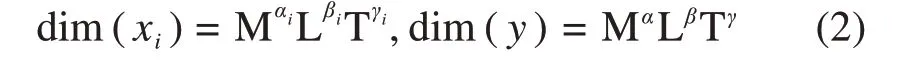
将各工况所选基本量记为xr,xs,xt，其待求指数分别为sir,sis,sit，对各参量做如下运算得到相应π量：

进一步考虑到土仓压力、剪切模量等参量与掘进总载荷间的正相关关系，将各π量相加，最终得到土、岩2种地质工况下包含一定潜在物理力学机理和量纲制约关系的总载荷无量纲模型框架，见式(4)和式(5)。

土类地质：

3 基于Lasso算法的工程实例计算与讨论

基于上述不同工况下的无量纲模型，将其输入回归算法约束参量训练过程，挖掘具体工程数据样本特征，得到适用于具体工程的定量模型。本文基于我国土、岩2类不同地质条件的4个工程实例进行载荷计算，讨论并验证模型的泛化性和方法的有效性。针对土类地质工况，讨论天津地铁3号线和9号线2个工程，所研究施工段长度分别约为200 m和900 m，主要涉及粉土、粉质黏土等地层，由土压平衡盾构施工；针对岩类地质工况，讨论吉林引松和引洮引水2个工程，所研究施工段长度分别约为600 m和9 700 m，主要涉及石英岩、花岗岩等地层，由TBM施工。

由于部分工程的原始数据文件中存在一些异常值，包括非稳定阶段数据、空推数据和离群值等，对模型有效识别造成干扰，在计算前对这类数据进行了判别和剔除。另外，考虑到各π量之间的量级存在较大差异，为避免其影响特征权重，通过小数定标规范化[1]将输入数据约束在0～10的范围内。

3.1 工程数据挖掘算法的确定

考虑到掘进工程数据往往具有含噪、多参量耦合、共线性等统计特征，一般无偏估计回归方法由于其求解过程涉及原始数据逆矩阵的直接计算，往往难以对这类工程数据分析给出有效解。因此，本文采用加入正则化“惩罚”项的有偏估计回归算法完成模型定量训练与识别。此类算法可以调整权重α寻找模型方差与偏差的平衡，改善回归求解质量[14−15]，如式(6)所示，当正则化因子取一范数时称为Lasso回归算法。掘进载荷是多影响参量建模问题，Lasso回归能够有效筛选关键参量简化模型，因此采用该算法训练掘进数据，识别定量模型。

其中：θ为待求系数；m为自变量个数；X和Y分别表示自变量与因变量的数据矩阵；α为超参数；ψ(θ)为正则化因子。本文基于Lasso回归算法的数据挖掘建模主要包括2部分：超参数选取和模型训练。

3.2 超参数选取

在Lasso算法训练模型的过程中，超参数设置是其核心，该值偏大会导致系数识别高偏差，增加模型预测误差；偏小时训练建模易受到噪声和参数共线性的影响，导致系数识别高方差，此时回归系数往往随抽样变化呈现较大波动。本文通过10折交叉计算与试算系数稳定性相结合的方式确定各工程Lasso回归的超参数值。10折交叉计算的基本思想是首先将数据集随机划分为10个数据量基本相同的子集，然后依次将其中9份作为训练集，剩余1份作为测试集进行模型训练，最后观察10次计算的结果[16]，应用该方法能够避免特殊抽样引起对α取值的误判。

以天津地铁3号线的总推力建模为例，如图2所示。首先，通过10折交叉计算获取模型预测误差随α的变化关系，可见模型误差稳定在较低值时α≤1×10−3。然后，在该范围内依据经验取2～3个值进行20次随机抽样试算，系数稳定性如图2内嵌图所示。考虑到惩罚项较小时更利于保留数据原始特征，在保证系数稳定性的前提下遵循α尽量小的原则，确定最终总推力模型训练的超参数取值为1×10−4。同理可确定其扭矩模型的超参数取值为1×10−3。通过该方法确定其他各工程超参数取值如下，天津地铁9号线：1×10−20(推力)和1×10−8(扭矩)；吉林引松工程：1×10−4(推力)和1×10−20(扭矩)；引洮引水工程：1×10−20(推力)和1×10−20(扭矩)。

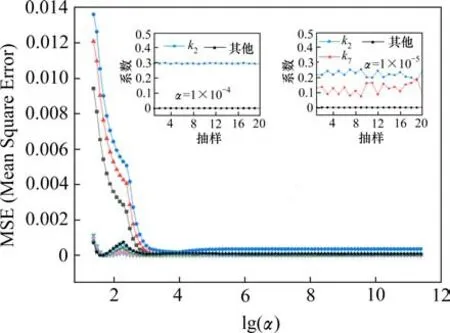
图2 天津地铁3号线总推力模型预测误差随超参数α的变化(内嵌图为不同超参数下系数随抽样的变化)Fig.2 Variation of total thrust model prediction error with superparameterαin Tianjin metro line 3

3.3 模型训练及结果讨论

将各工程数据分别通过随机抽样按7:3划分训练集和测试集，然后将掘进总载荷模型式(4)和式(5)分别代入土、岩2类地质工况下相应工程的训练集数据识别建模并在测试集上预测评估。主要通过决定系数R2(又称为拟合优度)和平均绝对百分比误差MAPE(Mean Absolute Percentage Error)评估模型预测效果。

图3给出了土、岩2类地质工况下各工程测试集上模型预测值与实测值的对比，同时给出了回归模型表达式及其拟合优度R2和预测平均绝对百分比误差MAPE，图中样本点序号为依据施工顺序对样本点的编号。图3(a)，3(b)，3(c)和3(d)结果表明，土类地质工况各工程中R2均大于0.95，MAPE均在15%以内，说明回归模型具有较好的拟合优度，能够基本反应实际工程的掘进总载荷值。图3(e)，3(f)，3(g)和3(h)结果表明，岩类地质工况各工程中R2最低为0.77，多数模型的拟合R2在0.85以上，MAPE均在30%以内，说明该工况下回归模型的预测值与实测值基本吻合。

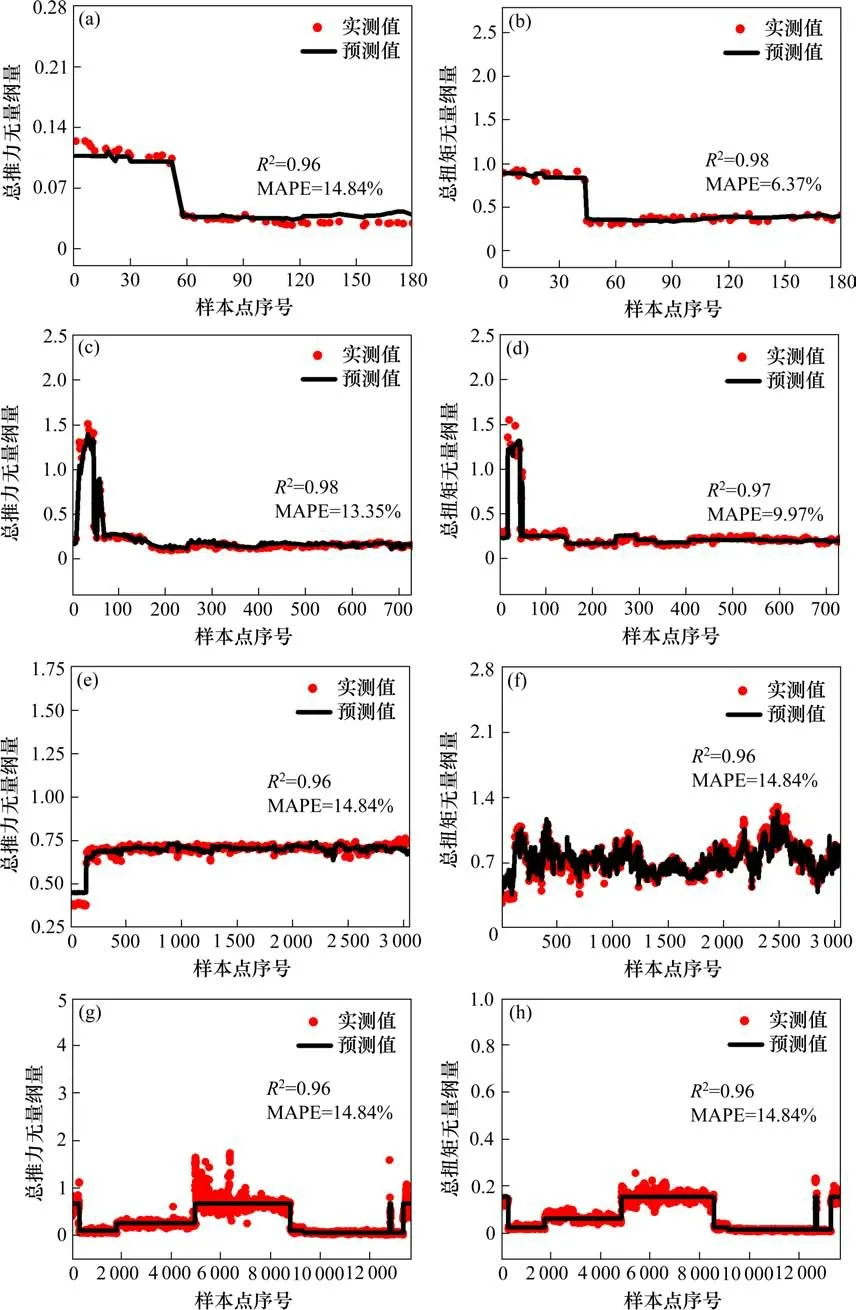
图3 不同工程中掘进载荷模型在测试集上的实测值与预测值对比Fig.3 Comparison of measured and predicted load values in test sets in different projects

为了进一步分析全集上量纲还原掘进载荷的预测误差，对载荷模型在全集上的预测百分比误差进行统计。图4给出了2种工况下不同工程中的掘进总载荷预测误差统计结果，天津地铁3号线中推力预测误差在30%以内的数据占81.8%，扭矩预测误差在15%以内的数据占96.1%；天津地铁9号线中推力、扭矩预测误差在30%以内的数据均占90%以上；吉林引松工程中，推力、扭矩预测误差在20%以内的数据占比均大于90%；引洮引水工程中推力预测误差在40%以内的数据占84.7%，扭矩预测误差在30%以内的数据占83.3%。各工程全集上的掘进总载荷预测MAPE均在30%以内。说明本文所述方法构建的预测模型能够较好地反映实际工程中掘进载荷的取值。

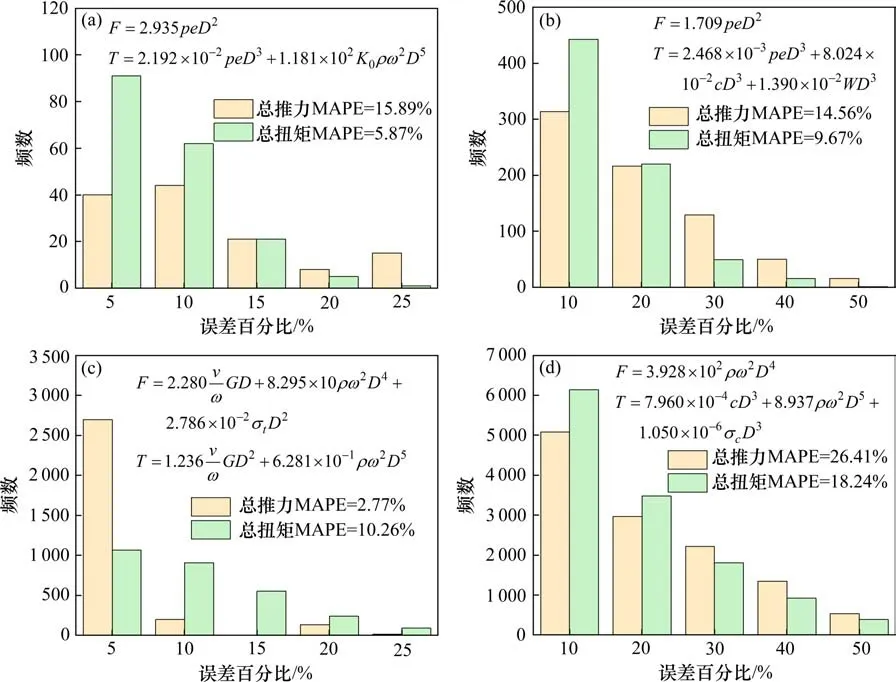
图4 不同工程掘进总载荷预测误差统计Fig.4 Statistic diagram of prediction error of load models in rock geological conditions

综上，由各工况不同工程中的建模及预测结果可知，基于量纲分析分别在土和岩类地质中构建的无量纲输入模型在相应工况各工程中均表现良好，说明该各工况的载荷模型具有一定泛化性。基于具体工程识别的回归模型可给出显式物理关系且均具有较好的预测效果，提高了数据挖掘模型的可解释性，同时表明本文建模方法具有一定有效性。

4 结论

1)以全断面隧道掘进机掘进总载荷为研究对象，提出一种量纲分析与数据挖掘相结合的参数建模方法。该方法基于量纲分析П定理的基本思想并结合力学分析搭建包含参量间物理制约关系的模型框架，进而输入到数据挖掘算法约束参数训练过程完成最终定量建模并获得显式模型，一定程度上提高了数据挖掘建模的可解释性与泛化性。

2)在量纲分析建模过程中形成一套针对掘进载荷建模的基本量选择方案，可为多变量问题的量纲分析提供参考：①优先考虑对目标量有关键影响的常数参量；②选择量纲相对“简洁”的影响参量；③结合具体问题分析参量间影响关系进一步确定基本量。在数据挖掘建模过程中分析选取Lasso算法训练模型，通过10折交叉计算与试算系数稳定性相结合的方式确定回归建模超参数，获得稳定有效的定量模型。

3)建立了土、岩2类典型地质工况的掘进总载荷模型，分别结合土类地质工况下的天津地铁3号线和9号线以及岩类地质工况下的吉林引松和引洮引水工程进行计算与讨论。通过对决定系数和百分比误差统计结果的分析，验证了模型的泛化性和适用性，表明本文的建模方法具有一定的有效性。本文工作可为全断面隧道掘进机的优化施工提供参考，同时为大型工程装备的多参量数据挖掘建模提供一种新思路。