一种基于三维坐标识别的逆变器开路故障诊断方法
2022-05-17罗屿李凯迪石英春
罗屿,李凯迪,石英春
(1.中南大学 交通运输工程学院,湖南 长沙 410075;2.深圳地铁运营集团有限公司,广东 深圳 518000)
逆变器在交通运输系统中应用广泛并举足轻重。然而,由于恶劣的工况及元件损坏,逆变器故障率长期居高不下。电容器、功率半导体开关是造成逆变器严重故障的主要原因,功率半导体开关的故障率现今有所下降,但故障率仍然很高,不能低估[1]。电力半导体开关故障可分为2类:短路故障与开路故障。短路故障引起过电流会对系统造成灾难性破坏,通过基于硬件电路来迅速保护系统安全。开关开路故障发生时故障特征不明显不易发现,会给系统带来安全隐患,本文主要研究逆变器的开路故障。近年来,电力半导体开关故障诊断方法主要有基于电压的方法和基于电流的方法。基于电压的方法,通过电压信号提取故障特征来实现逆变器故障诊断。CHENG等[2]对预设诊断特征量与电压包络线进行比较,实现单开关开路故障诊断,方法简单需要一定容错率。AN等[3]通过对正常情况和故障模式下的开关函数模型分析,以下管电压作为诊断量,但是需要系统触发信号,对系统改动要求高。张国恒等[4]以牵引逆变器输出电压和电流为处理对象,提取小波包熵特征,利用贝叶斯网络形成新的特征向量进行故障定位,该方法的计算复杂度高。WU等[5]提出了一种仅采用两路输出电压作为诊断变量快速的电压源逆变器多开路故障诊断方法。CHENG等[6]提出了一种基于鲁棒性开路开关结合共模电压分析定位的逆变器故障诊断方法。基于电压的诊断方法,避免了负载、频率等因素变化的影响,但需额外传感器等硬件辅助。而基于电流的方法通过收集输出相电流信号来实现故障诊断,不需要系统控制信号或额外的传感器。AN等[7]结合电流预测模型与混合逻辑动态模型对故障进行诊断,ZHANG等[8]以每相的相电流相角的异变进行故障判定,但文献[7]和[8]诊断均会受负载变化影响。HE等[9]监测直流母线中性点电流并结合瞬时开关状态与相电流信号建立故障特征监测机制,根据3项参数异动来实现故障定位。YAN等[10]通过零电压矢量重构三相电流作为故障特征量,由此进行逆变器的故障诊断及定位。但该类需要传感器的诊断方法在一些空间受限的场合应用局限性较大。WU等[11]构建直角坐标系电流轨迹,通过检测轨迹上几个连续点斜率与方向异常进行故障诊断。YANG等[12]通过分析三相电流相关性,将三相电流的协方差用于故障诊断和定位。SUI等[13]依据故障会改变开关状态,造成电流畸变的原理,将电流和开关状态结合进行故障诊断。陈勇等[14]通过比较三相电流测量值与观测值构建电流观测器,进行实时开路故障诊断与故障定位。CECATI等[15]将电流转化到特殊坐标系中形成轨迹,计算电流轨迹斜率联系故障表征实现诊断。这些方法在低电流值时存在误差或诊断时间长的缺点。现今的开路故障诊断方法虽各有优势,但铁路车辆使用的逆变器负载范围变化大,部分基于输出电流的诊断方法的故障定位会受到限制,基于系统控制信号或通过增加额外传感器来诊断故障的方法不利于工程实践。本文提出了一种基于三维坐标识别的逆变电源开路故障诊断的方法,将现有电流传感器采集三相输出电流,转换成三维坐标。开路故障时,三维坐标与原点的距离会发生变化,通过距离的变化可以对开路故障进行快速判断。以三维坐标系轨迹的形心作为故障特征对开关管开路故障进行定位。载荷变化对三维坐标系轨迹的大小有影响,通过归一化处理后,不影响定位故障结果。该方法具有诊断时间短和定位精准的特点。
1 基于坐标距离的故障判断
本文以两电平三相逆变器作为研究对象,如图1所示。逆变器采用PWM控制,开关管V1~V6为带反并联二极管D1~D6的全控型功率管,Za~Zc及La~Lc为等值的三相负载电阻与电感,即Ra=Rb=Rc=R,La=Lb=Lc=L,N为中性点。正常工作时,三相桥臂上下开关管交错通断输出相电流。以A相为例,A相上桥臂开关管导通,输出为正向相电流,反之A相桥臂输出电流为负向相电流。
正常情况下,逆变器输出电流为相位互差120°,幅值相等的正弦波,如式(1)。
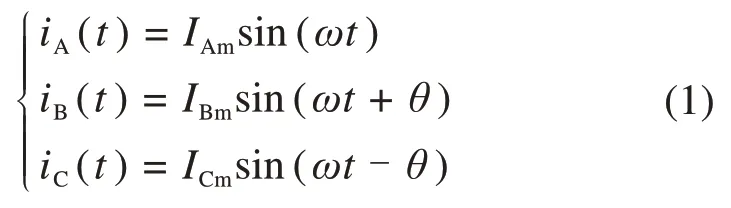
式中:IAm,IBm和ICm为三相电流幅值,且为相等的值Im;ω为电流角频率;θ为A,B两相电流之间的相位差。
考虑三相负载并计算,可得到相电压如式(2)。
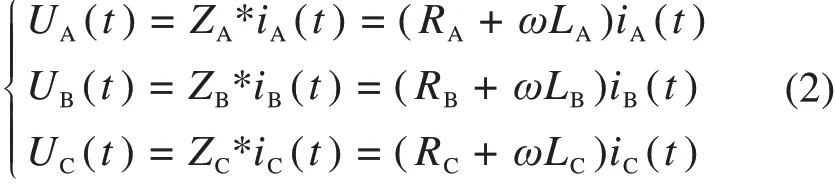
为了构建三相电流三维坐标故障诊断体系,本文将三相电流的值对应转化成三维坐标,并形成三维坐标下的轨迹。
令x=iA(t),y=iB(t),z=iC(t),为了方便化简,令α=x/Im,β=y/Im。则有:

将β展开后有:
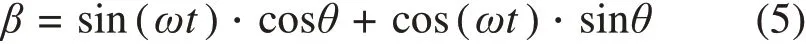
对α,β求平方可得:
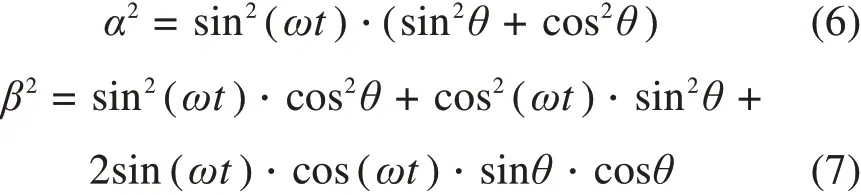
式(6)和式(7)相加可得式(8)。
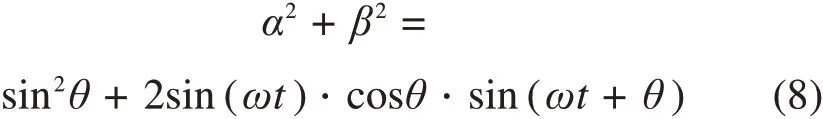
结合式(1),(2)对式(8)化简后可得:
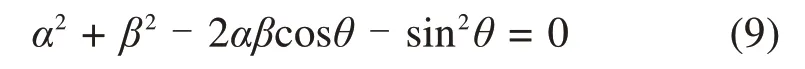
转化到x,y的表达式即为式(10)。
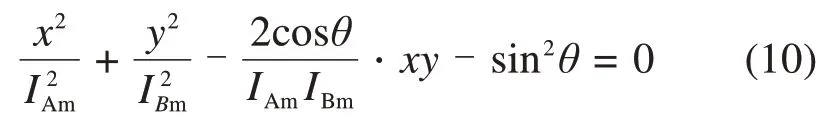
式中:x∈[-IAm,IAm],y∈[-IBm,IBm]。
已知二次曲线为:
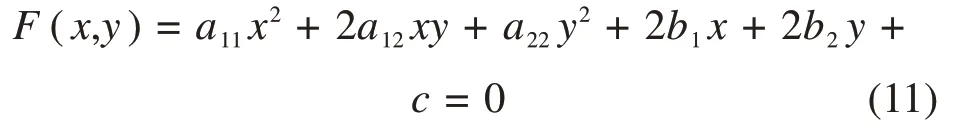
其曲线类型可通过判别式(12)判定:

若Δ>0为椭圆,Δ<0为双曲线,Δ=0为抛物线。对于式(8):
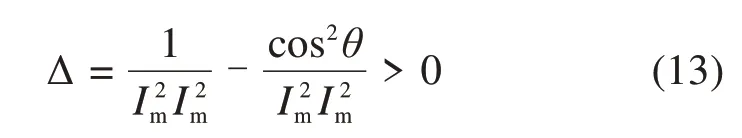
因此式(10)为中心位于坐标原点的椭圆一般方程。
由三相电流平衡iA(t)+iB(t)+iC(t)=0可得:

将式(10)与式(14)结合得三维坐标曲线方程式。

式(15)为三维坐标系的一个椭圆环。
由坐标距离可知,三维坐标中相电流对应的点与坐标原点的距离可表示为式(16)。
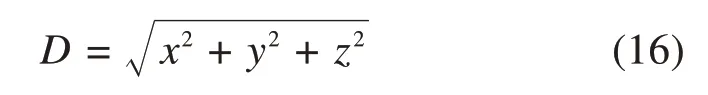
其中,x+y+z=0
功率管发生开路故障时,如果对应的输出相电流是由其导通产生的,则该相电流会因为功率管开路故障的影响幅值降为0。因此,故障相电流三维坐标点F(xf,yf,zf)与原点O(0,0,0)距的Df的值也会减少。
如图2所示,故障点F在椭圆上的投影为F′,直线OF′与椭圆的交点为S点。

图2 开路故障三维坐标示意图Fig.2 3D coordinate diagram of open-circuit fault
由椭圆公式(15),椭圆所在平面方程为式(17)。

可得点F到平面的投影点F′(xf′,yf′,zf′)为:
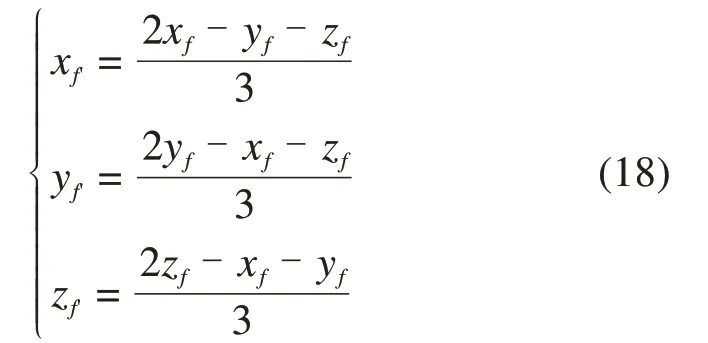
直线OF′2点的直线方程为式(19)。
由式(15)与式(19)联合可得到直线与椭圆的交点坐标为S(xs,ys,zs)。
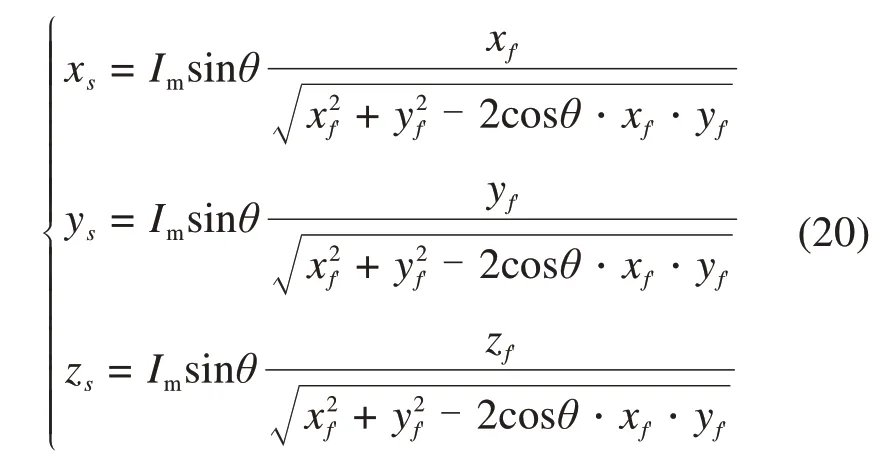
可得S点到原点的距离Ds为式(21)。
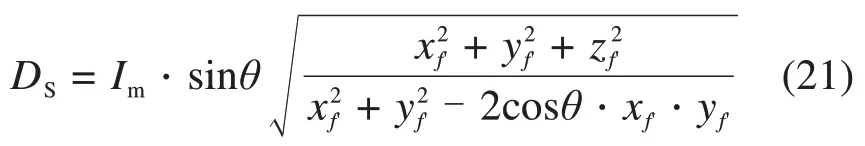
DS是三相电流正常运行情况下的理论值,逆变器开关管的开路故障出现在正在工作相时,会导致工作相电流的输出幅值为0。这时对应的三维坐标距离值会比理论值小,因此本文构建构建逆变器开路故障判断比值函数Fun,如式(22)。
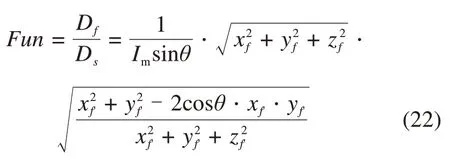
由于工程实际中以及防止误报警,本文取0.9作为判定的阈值,逆变器开路故障判定比值函数为:

Fault值等于0时,无故障发生,Fault值等于1时,逆变器发生开关管开路故障。
由故障判定公式(23)可以迅速判断出逆变器发生开路故障,但无法对故障的类型进行精准定位。因此本文引用形心坐标的概念对开路故障进行故障定位。
形心的定义为n维空间对象的几何中心,三相电流椭圆环的形心坐标计算式(24)。

2 逆变器开路故障定位
开关管发生开路故障时,逆变器中各相电流会发生变化,从而对应的三维坐标系轨迹也会形变。本文将从单开关管故障,同相双开关管及异相双开关管故障展开故障定位研究。
2.1 单开关管故障
若A相电流正半周期时V1开关管发生故障,A相开关管状态为V1导通,V2关断,输出电流受影响。在负半周期发生故障时,由于A相V1关断,V2导通,A相正常工作,电流保持不变。因此进行分段讨论。
当ωt∈[2kπ,2kπ+π)时V1发生开路故障,A相受V1断路影响,相电流为0,在星型RL负载中,可得B相电流。
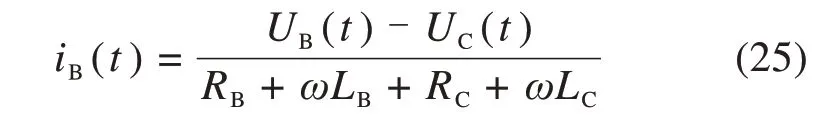
结合式(1)~(2),可得:
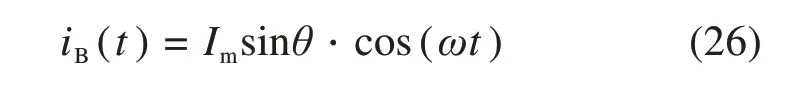
由于三相电流平衡,iA(t)=0则,iB(t)=−iC(t),所以有:
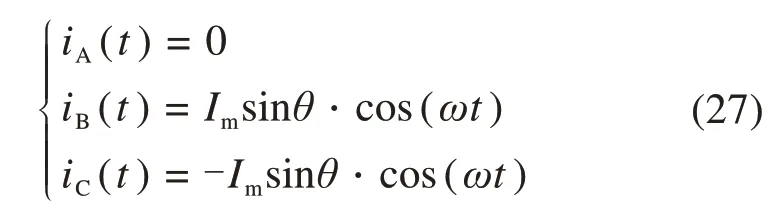
将式(27)转化为三维坐标方程式(28)。

当ωt∈[2kπ+π,2kπ+2π)时,A相电流输出由V2导通获得,V1断路不影响A相电流输出,轨迹与正常情况下保持一致,如式(10)。
V1发生故障,在ωt∈[2kπ,2kπ+π)阶段为式(28),为直线段轨迹,在ωt∈[2kπ+π,2kπ+2π)阶段为部分椭圆轨迹。
结合公式(10),(24),(28),可得轨迹形心坐标(XV1,YV1,ZV1)。
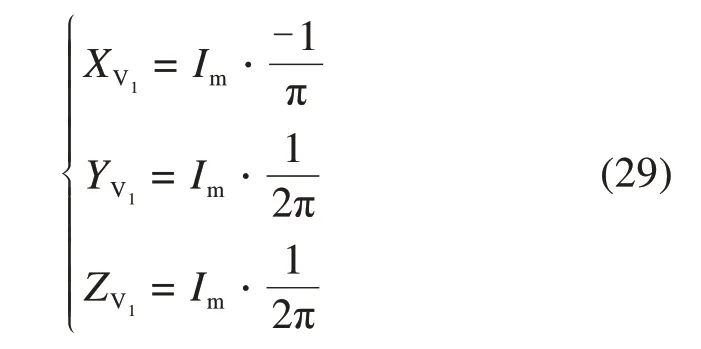
由式(29)可知,形心坐标的三维都是Im的倍数,故可以进行归一化处理得式(30)。

由式(30)可知,归一化后的形心坐标为固定值,不受负载变化的影响。
同理可得到V2~V6开关管开路故障时的形心坐标。建立单开关管开路障定位表如表1。

表1 单开关管开路故障定位表Table 1 Single switch open circuit fault location
2.2 同相双开关管故障
V1V2同相开关管开路故障时,A相会一直处于断路状态,A相电流为0,则输出电流可以表示为:
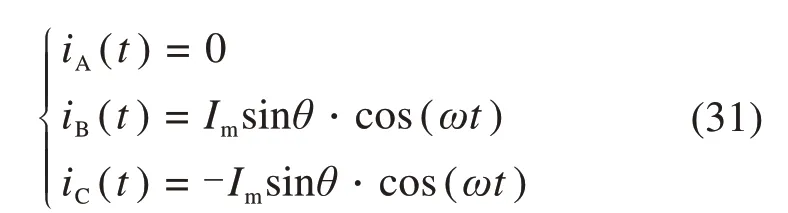
式中:ωt∈[2kπ,2kπ+2π],这时三维坐标系轨迹发生形变,表达式为:
由式(32)知,当同相双开关开路故障时,三维坐标系轨迹会变成一条直线段,且当故障分别发生于A,B,C相时,三维坐标系轨迹将为分别垂直于X,Y,Z轴的直线段,形心为原点。
为了进行故障定位,在确定故障三维轨迹的形心为原点时,利用方向矢量对故障进行定位。本文选择任意此时三维坐标系轨迹上3个点两两作差,得到的方向矢量作为故障特征进行定位。同相双开关管发生故障时,三维坐标系的故障定位表可总结为表2。

表2 同相双开关管开路故障定位表Table 2 Open circuit fault location table of same-phase two-switch
2.3 异相双开关管故障
异相V1V3开路故障时,开路的故障时间为半个周期,相电流每相存在2π/3相位差,需分段进行分析。
当ωt∈[2kπ,2kπ+2π/3]时,V1故障会导致正半周期的A相电流变为0,V3故障对处于负半周期B相电流无影响。则输出电流可表示为式(33)。
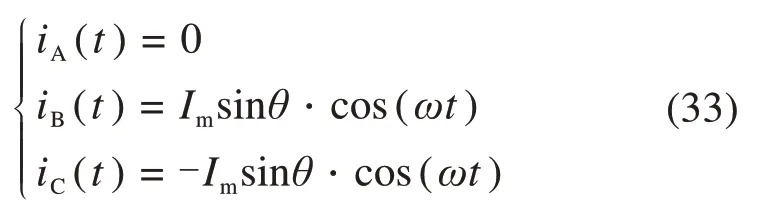
当ωt∈[2kπ+2π/3,2kπ+π]时,V1故障会导致A相正半周期的电流变为0,V3故障会导致B相正半周期的电流变为0,根据三相电流平衡有iC(t)=0,故输出电流为iC(t)=iB(t)=iC(t)=0。
当ωt∈[2kπ+π,2kπ+5π/3]时,V1故障对处于负半周期A相电流无影响,V3故障会导致B相正半周期的电流变为0,故输出电流可表示式(34)。
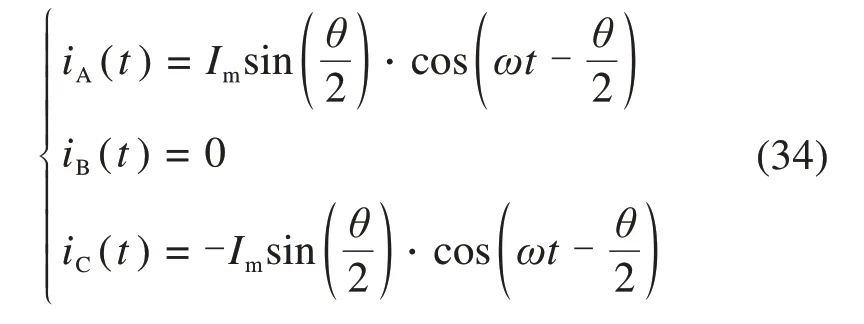
当ωt∈[2kπ+5π/3,2kπ+2π]时,V1V3故障故障对处于负半周期AB相电流无影响,逆变器正常工作,故输出电流可表示为式(10)。
与上述单管故障处理方法一致,以V1V3开路故障为例,依据公式(1),(24),(33)和(34),可得到归一化的形心坐标。根据当前三维坐标系轨迹形心是否落入区域来判定是否发生了V1V3开路故障。异相双开关管发生故障时,开路故障的故障定位表可总结为表3。
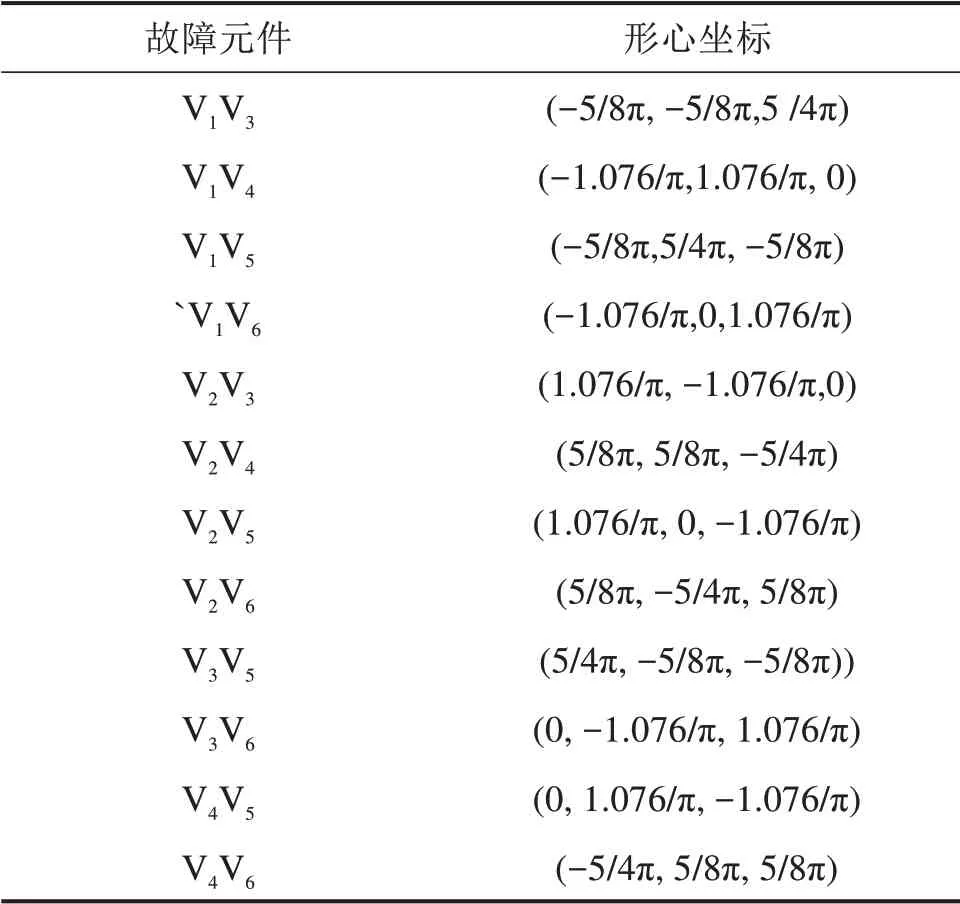
表3 异相两开关管开路故障定位表Table 3 Open circuit fault location table of two-phase switch
本文所提的基于三维坐标系轨迹的多开关故障定位方法诊断从以下3个步骤展开:
1)采集逆变器的三相输出电流,将三相电流转化为三维坐标。
2)计算三维坐标的距离,依据故障判定公式的Fault值判断逆变器是否开关管发生开路故障。
3)计算形心坐标,如果形心为原点,计算方向矢量参照同相故障定位表定位故障,如果不为原点,参照单管和异相双管故障定位表故定位故障。
由于工程实际中存在测量误差和信号干扰等因素,且每个故障定位区域之间相互不发生重叠,应在故障形心周围应设置一定范围的诊断区域,该区域的半径设为2%归一化后的电流幅值。
3 实验结果分析
本文基于dSPACE半实物实验平台设置了3组针对本文所提故障诊断判断和定位方法的验证实验。诊断实验平台原理如图3所示。

图3 实验平台原理图Fig.3 Schematic diagram of the experimental platform
该平台主要组成部分为:三相桥式逆变电路,电子负载箱,dSPACE半实物实验平台。系统控制信号由计算机产生通过dSPACE传递至逆变电路,dSPACE监控每一相的电流信号通过传回计算机进行处理,该实验平台主要实验参数为输入直流电压600 V,输出交流电压三相380 V,输出电流频率为50 Hz,负载3.8 kW×3,负载功率因数为0.95。
本文在此实验平台上开展了3组实验,分别为单开关管开路故障,同相双开关管开路故障与异相双开关管开路故障。对应3组实验的故障判断图分别为图(4),图(5)和图(6),故障诊断结果汇总为表(4)。
由图(4)可知,故障发生在t=0.19 s,故障判断函数值Fault的值变为1的时间t1=0.208 s,故障响应时间为0.018 s,在0.14个周期判断出逆变器发生开路故障。
分析图(7),故障发生在t=0.25 s,故障判断函数值Fault的值变为1的时间t2=0.252 s,故障响应时间为0.002 s。计算故障形心坐标,其为原点,故进行方向矢量判断。
图(6)故障发生在t=0.32 s,故障判断函数值Fault的值变为1的时间t3=0.346 s,故障响应时间为0.026 s,在0.20个周期判断出逆变器发生开路故障。
为了对开路故障发生的开关管进行定位,本文对故障发生后的故障轨迹形心坐标进行计算,结果如表4所示,参照故障定位表,实验一形心坐标对应V1故障。实验二形心坐标矢量对应V3V4故障方向矢量。实验三形心坐标与V1V6故障形心坐标对应,3组实验故障均得到准确定位。

表4 逆变器开关管故障诊断结果Table 4 Inverter switch tube fault diagnosis results table

图4 单相开关管故障判断图Fig.4 Single phase switch fault judgment diagram
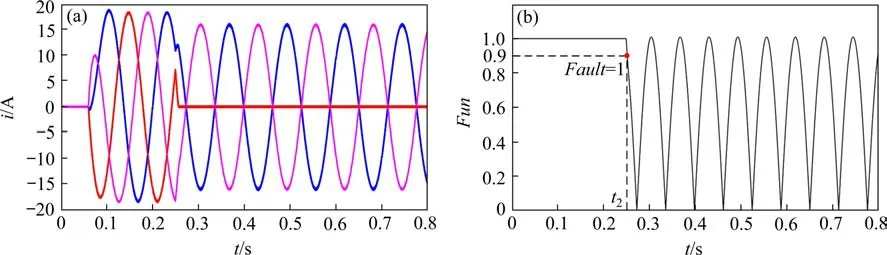
图5 同相双开关管故障判断图Fig.5 Same-phase two-switch fault judgment diagram
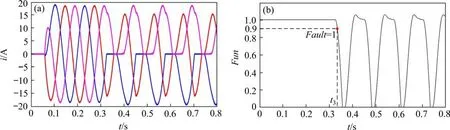
图6 异相双开关管故障判断图Fig.6 Heterophase two-switch fault judgment diagram
综合上述3个实验可知,通过三维距离的方法可迅速对逆变器开路故障做出判断,通过计算形心坐标对应故障定位表可对逆变器的不同类型的开关管开路故障进行故障定位。
4 结论
1)本文基于逆变器开关管发生开路故障时,输出相电流在三维坐标系中的成像会产生规律变化提出了一种逆变器开路故障诊断方法。
2)本文方法利用输出相电流进行故障判断,无需增加额外的传感器和逆变器的控制信号。
3)通过半实物仿真平台进行不同类型的逆变器开关管开路故障实验,验证了本文方法的有效性。该方法能迅速判断逆变器发生开路故障并准确定位。
4)下一步将利用三维坐标的其他特征变化来优化诊断方法。
