变摩擦转向架斜楔等效刚度计算及应用

刘嘉兴，吕大立,3，吕可维，张琪昌，李玉龙

(1.天津大学 机械工程学院，天津 300072；2.天津市非线性动力学与控制重点实验室，天津 300072；3.天津大学 内燃机研究所，天津 300072；4.中车齐齐哈尔车辆有限公司 大连研发中心，辽宁 大连 116042)

对斜楔减振器的计算处理是研究三大件货车转向架动力学性能的重点及难点[1]，与转向架其他部件相比，斜楔减振器的质量几乎可以忽略不计，因此通常会被当成一个简单力元来处理，然而简单的力元并不能完全体现斜楔的非线性摩擦特性和对载荷敏感的特性，因此有较多学者对斜楔的建模处理及动力学性能进行了细致地研究。国内外学者对斜楔的处理模型可以分为3种类型：组合模型，多体动力学模型和准静态模型[1]。组合模型是从斜楔的作用原理上，将斜楔用刚度元件、摩擦阻尼元件及其他作用元件耦合的力元模型代替，DURALI等[2-3]在组合力元上做了深入的研究。与简单力元相比，组合力元的作用元件更多，考虑的因素更多，与实际情况更接近一点，但由于组合模型是斜楔在作用原理上的等效模型，对斜楔的实际参数分析和优化仍有一定的局限性。多体动力学模型又称MBS模型，是根据转向架斜楔的实际模型参数在多体动力学软件中建立的转向架斜楔动力学模型。多体动力学模型在模拟列车运行状态和分析列车运行时的安全性、稳定性和舒适性等方面起着不可替代的作用，这是另外2种模型无法做到的。国内外有许多学者对MBS模型的建模方法进行了探究[4-9]，力求建立与实际情况更接近、更简便的多体动力学模型。由于斜楔、侧架和摇枕三者之间的位移非常小，发生的过程比较缓慢，因此斜楔滑动过程可假定是准静态的，通过对斜楔、摇枕和侧架进行静力平衡分析，可建立斜楔准静态模型[1]。由于斜楔准静态模型是根据斜楔的实际几何参数进行静力平衡分析，因此根据斜楔准静态模型可以对斜楔几何参数进行分析优化。国内外有较多学者根据斜楔准静态模型研究斜楔的各项几何参数对斜楔性能的影响，王勇等[6]研究了变摩擦减振器的工作原理；朴明伟等[10]研究了斜楔摩擦力在垂向和纵向减载中的作用；冯东喆等[11]从摩擦功的角度探究了斜楔角对斜楔减振性能的影响；杨利军等[12]探究了斜楔顶角与斜楔副摩擦面正压力的关系；PANDEY等[13]研究了转向架缓冲力、斜楔摩擦因数对侧架侧向力的影响。综上，3种模型中除组合模型外，MBS模型与准静态模型都有各自的优势，MBS模型可以研究斜楔的动力学性能，准静态模型可以对斜楔几何参数进行优化分析。目前对MBS模型的研究主要集中在建模方法的探究，而对于准静态模型，主要分析斜楔几何参数对斜楔接触面摩擦力和压力的影响。然而斜楔提供的各向等效刚度，如：纵向刚度、抗菱刚度等，是斜楔的重要力学性能，斜楔刚度参数是否准确对斜楔MBS模型的准确性也有很大的影响，却没有人进行系统的研究分析，只有极少数人对斜楔的单个刚度进行研究。胡旱青等[14]推导了K6转向架斜楔的等效纵向刚度，通过比较整车临界速度间接验证等效纵向刚度的准确性，但间接验证的方法容易引入其他不确定因素。王春山等[15]推导了斜楔的抗菱刚度，但缺少数据验证。因此，本文以转K6型转向架为研究对象，对斜楔进行准静态分析，系统研究斜楔的垂向刚度、纵向刚度、横向刚度及抗菱刚度，建立转K6型转向架有限元模型，对理论结果进行验证，并将斜楔刚度输入货车多体动力学模型中探究斜楔刚度对货车多体动力学性能的影响。

1 模型简化

转K6转向架物理模型如图1(a)所示，简化模型如图1(b)所示。斜楔与侧架的接触面为主摩擦面，与水平面垂直；斜楔与摇枕的接触面为副摩擦面，与水平面的夹角为α。由于本文研究斜楔提供的各向等效刚度，且在加载与减载过程中，斜楔、摇枕和侧架的变形量与三者位移相比很小可忽略。因此本文做如下简化处理：假定斜楔、侧架与摇枕均为刚体；只考虑斜楔弹簧作用，不考虑摇枕弹簧作用；不考虑斜楔与摇枕斜楔槽侧面的间隙。

图1 转K6型转向架示意图Fig.1 Schematic diagram of ZK6 bogie

2 斜楔刚度理论计算

2.1 垂向刚度

当摇枕作用垂向力时，转向架受力如图2所示。图中FC0表示摇枕预加载力，引起斜楔弹簧的预压缩量为y0；FC表示作用于摇枕的垂向力，向下为正；FP表示斜楔弹簧作用力；FR1表示侧架对前斜楔的侧压力；FN1表示摇枕对前斜楔的侧压力；μ1表示主摩擦面的摩擦因数；sign(v)μ1FR1表示侧架对斜楔的摩擦力；v为摇枕垂向速度，向下为正；sign为符号函数，当v为正时，摩擦力为如图2所示方向，否则与图示方向相反。

图2 转向架垂向加载受力图Fig.2 Vertical loading force diagram of bogie

由于转K6转向架主摩擦面垂直水平面，因此侧架宽度保持恒定，当摇枕作用恒力F1时，摇枕与斜楔都向下运动，摇枕和斜楔总的有效宽度保持不变，两者并无相对运动趋势，因此摇枕与斜楔之间无摩擦力作用。王勇等[6,10]也对斜楔垂向作用进行了分析，但在主摩擦面垂直水平面，侧架宽度保持恒定的情况，引入了副摩擦面摩擦力，本文将通过有限元模型对这2种情况进行验证。

首先对前斜楔在x轴和y轴上进行静平衡分析，得到：

由式(2)得到侧架对斜楔的侧压力FR1和斜楔弹簧提供的变形力FP的关系：

对转向架整体进行受力分析，在y轴上，4个斜楔受到的外力是一样的，因此在y轴上有：

式中：斜楔弹簧力FP与斜楔垂向位移y关系为：

式中：ks表示斜楔弹簧垂向刚度；y0为斜楔弹簧的预压缩量。

由于摇枕与弹簧无相对运动，因此斜楔垂向位移y也为摇枕垂向位移。联立式(2)和(3)，得摇枕垂向力FC与摇枕垂向位移y的关系：

摇枕垂向力FC对垂向位移y求导，可得斜楔提供的垂向刚度：

2.2 纵向刚度

当斜楔弹簧预压缩量为f，摇枕发生纵向位移x时，转向架受力如图3所示。FQ1表示前斜楔弹簧所提供的力；FQ2表示后斜楔弹簧所提供的力；h为摇枕发生纵向位移x时，斜楔的垂向位移。前后斜楔受力如图4所示，图中μ1表示主摩擦面的摩擦因数，μ2表示副摩擦面的摩擦因数。由于摇枕纵向移动过程中，斜楔与摇枕间会发生相对滑动，因此斜楔与摇枕间有摩擦力作用。

图3 转向架纵向加载受力图Fig.3 Longitudinal loading force diagram of bogie

图4 纵向加载前后斜楔受力图Fig.4 Longitudinal loading force diagram of front and rear wedge

首先对前后斜楔在x轴和y轴上进行静平衡分析，得到侧架对斜楔的侧压力与斜楔弹簧变形力的关系：

式中：

前后斜楔弹簧提供的变形力可表示为：

式中：f表示斜楔弹簧预压缩量；h表示摇枕发生纵向位移x时引起的斜楔垂向位移。

对转向架整体进行位移分析，得到摇枕纵向位移x与斜楔位移垂向位移h的关系：

对转向架整体进行纵向受力分析，摇枕受到的纵向力Fz可表示为：

将式(7)、(10)、(11)代入式(12)，得到摇枕纵向力Fz与摇枕纵向位移x之间的关系：

作用于转向架的纵向主动力Fz对摇枕纵向位移x求导，得到斜楔提供的纵向刚度kz：

式中：A和B由式(8)和式(9)确定。

2.3 横向刚度

当转向架摇枕作用横向力时，转向架整体受力如图5所示，图中，FH表示摇枕受到的横向力，FPH表示斜楔受到的横向弹簧力，FRH表示侧架对斜楔的横向摩擦力，FNH表示斜楔与弹簧之间的相互作用力，包含副摩擦面摩擦力及两者间的横向正压力。

图5 转向架横向加载受力图Fig.5 Transverse loading force diagram of bogie

假设转向架横向加载过程中摇枕和斜楔均未发生垂向和纵向位移，且发生的横向位移在转向架横向约束限制的范围内。

对转向架整体进行受力分析，得：

式中：FPH可表示为：

式中：kH表示斜楔弹簧的横向刚度；z表示斜楔的横向位移，由于斜楔与摇枕在横向加载过程中相对位置保持不变，因此z也表示摇枕的横向位移。

于是有：

由于侧架对斜楔的横向摩擦力FRH与侧架对斜楔的正压力有关，而由垂向刚度的推导过程可知，侧架对斜楔的正压力大小只与斜楔垂向预压缩量有关，因此横向摩擦力FRH中并不包含横向位移z。于是作用于转向架的横向主动力FH对摇枕横向位移z求导，得到的斜楔等效横向刚度kh为：

2.4 抗菱刚度

抗菱刚度定义如图6所示，两侧架前后错动而使转向架产生菱形变形，抗菱刚度即为抵抗这种菱形变形的刚度[15]。当转向架发生菱形变形时，摇枕与侧架的相对位置由垂直变为倾斜，侧架宽度为L不变，摇枕与斜楔的纵向宽度变窄，两斜楔被挤向摇枕中央，斜楔沿副摩擦面向下运动，当侧架相对摇枕转动θ时，两斜楔作用于侧架的力F1在侧架中心产生的力矩M，即斜楔抵抗菱形变形对侧架产生的力矩。

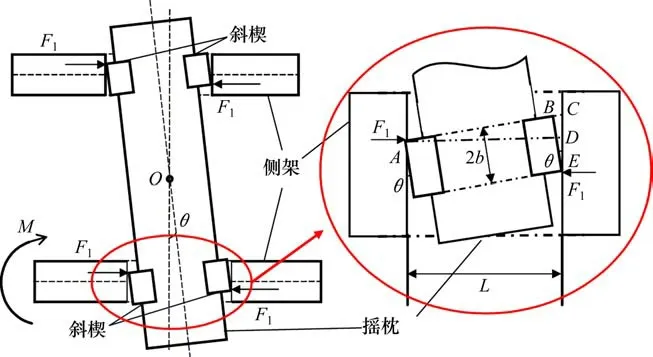
图6 转向架斜楔抗菱刚度示意图Fig.6 Schematic diagram of anti-warp stiffness of bogie wedge

如图6所示，当侧架相对摇枕转动角度θ时，摇枕与斜楔的纵向宽度由AD变为AB，摇枕与斜楔的减少的纵向宽度2Δx为：

式中：AC=AD/cosθ；BC=BEtanθ；BE=2b为斜楔宽度；AD=L。于是有：

当θ很小时，cosθ=1，tanθ=θ，于是有：

由于侧架上两斜楔对称，因此单侧斜楔的纵向位移为Δx，对单侧斜楔进行位移分析，如图7所示，斜楔垂向位移与纵向位移关系为：

图7 斜楔抗菱刚度受力图Fig.7 Anti-warp stiffness force diagram of wedge

对斜楔进行受力分析，得到侧架对斜楔的力F1与斜楔垂向弹簧力F2的关系：

斜楔垂向弹簧力F2可表示为：

当侧架相对于摇枕转动的角度θ很小时，作用于侧架的中心力矩可表示为：

将式(23)、(24)代入式(25)，可得作用于侧架中心的力矩M与侧架转角位移θ的关系：

作用于侧架中心的力矩M对侧架转角θ求导，得到斜楔提供的抗菱刚度：

3 斜楔刚度有限元模拟验证

在完成斜楔等效刚度的理论计算之后，运用ABAQUS软件建立转K6转向架模型，对斜楔各向刚度的理论公式进行验证。根据转K6转向架的外形尺寸，略去不影响计算结果的微小特征，模型总计划分106 986个六面体单元，126 148个节点。为了更好地对比验证，只设置斜楔弹簧单元，摇枕下其他弹簧组作用不考虑，根据转K6转向架参数，空车时斜楔弹簧垂向和横向刚度分别为202.7 N/mm和110.9 N/mm。斜楔摩擦面法向均设为硬接触，主摩擦面摩擦因数为0.25，副摩擦面摩擦因数为0.3。

3.1 垂向刚度验证

在建立转向架有限元模型后，对转向架施加垂向边界条件，在摇枕上施加垂向加载力和减载力，提取摇枕位移与理论公式(5)计算得到的位移进行对比，结果如表1和表2所示。在转向架有限元模型斜楔副摩擦面设置摩擦因数的情况下，垂向加载与减载模拟位移均与理论位移吻合，验证了理论结果的准确性。在转向架垂向作用过程，斜楔主摩擦面垂直底面的情况下，斜楔副摩擦面无摩擦力作用。

表1 转向架垂向加载模拟结果Table 1 Vertical loading of bogie by finite element simulation

表2 转向架垂向减载模拟结果Table 2 Vertical load reduction of bogie by finite element simulation

3.2 纵向刚度验证

对转向架有限元模型施加纵向加载边界条件，对斜楔弹簧施加一个垂向预压缩量后，对摇枕施加纵向位移，提取摇枕的纵向力与理论公式(32)计算得到的纵向力进行对比，结果如表3所示，4组模拟结果均与理论结果吻合。

表3 转向架纵向加载模拟结果Table 3 Longitudinal loading of bogie by finite element simulation

3.3 横向刚度验证

由于转向架在横向加载过程中，斜楔弹簧有横向作用，因此对斜楔设置横向弹簧单元，刚度为100.4 N/mm，并设置转向架横向边界条件。对摇枕施加横向作用力，提取摇枕的横向位移与理论公式(17)计算得到的横向位移进行对比，结果如表4所示，4组模拟结果均与理论结果吻合。

表4 转向架横向加载模拟结果Table 4 Transverse loading of bogie by finite element simulation

3.4 抗菱刚度验证

由于转向架发生菱形变形时，两侧架受力情况关于转向架中心对称，为节约时间成本，只模拟计算一个侧架的抗菱变形，设置转向架抗菱边界条件，对斜楔弹簧施加垂向预压缩量后，对侧架施加绕垂直方向的转角位移，提取摇枕转动角度及力矩，并与理论公式(26)计算得到的力矩进行对比，结果如表5所示。

表5 转向架抗菱加载模拟结果Table 5 Anti-warp loading of bogie by finite element simulation

由表5可知，侧架转动角度越小，理论计算结果与有限元结果越接近。本文推导斜楔抗菱刚度的过程中，运用了小角度假设，即角度越小，本文理论推导的抗菱刚度越适用，这与理论结果和有限元结果吻合程度显示的趋势一致，验证了本文抗菱刚度理论公式的准确性。

4 斜楔等效刚度应用

4.1 自锁分析

斜楔摩擦减振器对转向架起着重要的减振作用，当斜楔发生自锁时，将无法起到缓冲减振作用而对车体造成巨大的危害。因此在验证了理论模型的合理性后，本文将从斜楔等效刚度的角度对斜楔自锁情况进行分析，首先对垂向刚度进行分析，根据式(6)，由垂向加载刚度大于0，得到：

当式(28)不满足时，垂向加载刚度小于等于0，对摇枕施加垂直向下的主动力时，斜楔弹簧不能发生垂直向下的位移，即转向架斜楔垂向发生自锁。从摩擦自锁原理上对此自锁条件进行分析，如图8所示，当斜楔从起始位置开始垂向加载时，阻碍斜楔向下运动的弹簧力为0，忽略斜楔重力影响，斜楔受到的主动力只有FN1，当式(28)不满足时，主动力FN1的作用线刚好在主摩擦面的摩擦角内，斜楔发生自锁，验证了从刚度计算角度分析斜楔自锁的可行性。

图8 斜楔自锁示意图Fig.8 Schematic diagram of self-locking wedge

由式(28)，根据转K6转向架参数，斜楔角α=58°，因此需保证斜楔主摩擦因数μ1<0.624 9，斜楔不发生自锁。

对垂向减载刚度进行自锁分析，根据式(6)，垂向减载刚度恒大于0不存在自锁的情况。

对纵向刚度进行分析，根据式(8)、(9)、(14)，由纵向刚度大于0，得到：

式(29)为0时确定的曲面如图9所示，斜楔角度α，主摩擦因数μ1及副摩擦因数μ2的取值应在图示曲面下，才能保证纵向刚度大于0。

图9 斜楔纵向自锁参数取值范围Fig.9 Range of wedge longitudinal self-locking parameters

根据转K6转向架参数，当斜楔副摩擦面与水平面夹角α=58°(α=1.012 rad)时，式(29)的等高线图如图10所示，为保证式(29)成立，μ1和μ2的取值应在图示0等高线以下区域，即α=58°(α=1.012 rad)的平面与图9所示曲面的交线以下区域。

对横向刚度进行自锁分析，根据式(18)，横向刚度恒大于0不存在自锁的情况。

对抗菱刚度进行自锁分析，根据式(27)，抗菱刚度恒大于0不存在自锁的情况。

综上，综合考虑斜楔各向刚度自锁情况，根据转K6转向架参数，当斜楔夹角α=58°时，主摩擦因数μ1和副摩擦因数μ2的取值应在图10所示0等高线以下区域，且保证斜楔主摩擦因数μ1<0.624 9。

图10 转K6斜楔纵向自锁摩擦因数取值范围Fig.10 Value range of friction coefficient of ZK6 longitudinal self-locking wedge

4.2 轮对横移量分析

为探究斜楔等效刚度对整车动力学性能的影响，运用Simpack软件，根据C70E货车参数，建立包含转K6转向架的C70E货车空车模型如图11所示。

图11 C70E货车空车动力学模型Fig.11 Dynamics model of empty truck of C70E

在Simpack软件中，使货车通过有初始激励的路段，分析货车在不同运行速度下货车轮对横移量来计算货车的临界速度。由中车齐齐哈尔车辆有限公司实际测得的C70E货车空车时的临界速度范围为140～150 km/h，当货车空车动力学模型未输入斜楔等效刚度时，整车第1和第3轮对的横移量如图12所示，轮对横移量在121 km/h时趋于收敛，在122 km/h时处于临界状态，因此在未输入斜楔等效刚度时，货车空车临界速度为122 km/h，与实测的临界速度有不小的差距。

图12 未输入斜楔等效刚度的轮对横移量Fig.12 Transverse displacement of wheelset without wedge equivalent stiffness

根据斜楔各等效刚度公式，代入转K6转向架空车时的斜楔参数。将计算得到的斜楔等效刚度输入到C70E货车动力模型时，整车轮对横移量如图13所示，在135 km/h时处于临界状态，因此输入斜楔等效刚度后的货车空车临界速度为135 km/h，与实测临界速度140～150 km/h相比，差距很小。

图13 输入斜楔等效刚度的轮对横移量Fig.13 Transverse displacement of wheelset with wedge equivalent stiffness

综上，斜楔等效刚度的输入提高了铁路货车多体动力学分析的准确性，使货车多体动力学模型与实际货车动力学性能更接近，对货车动力学性能后续的分析提供了准确的模型基础；同时也进一步说明了斜楔等效刚度对货车动力学性能影响很大，本文提出的斜楔各向等效刚度的计算方法在进行货车多体动力学分析时有重要意义。

5 结论

1)根据理论力学知识，系统地演算出了转向架斜楔各向等效刚度的解析表达式；利用有限元仿真建立了斜楔各等效刚度的数值计算方法，通过解析与数值方法的结果对比，相互验证了2种方法的准确性。同时发现在现有结构形式下，即侧架壁垂直的情况，转向架垂向加载与减载过程中，斜楔副摩擦面存在摩擦力的假设是不正确的。

2)从斜楔等效刚度层面提出了斜楔自锁的判断方法，得到斜楔不发生自锁时斜楔角度和摩擦因数的取值范围；根据刚度判断斜楔自锁的方法为转向架斜楔设计时参数的选择提供一种新的判断标准。

3)建立了货车整车多体动力学模型，根据临界速度计算结果，输入斜楔等效刚度后的货车临界速度更接近实际情况。本文提出的斜楔等效刚度的计算方法为铁路货车多体动力学建模时斜楔刚度参数的设置提供了理论支撑，弥补了在建立模型时斜楔各向等效刚度设置方面的理论指导空白，进一步提升了铁路货车动力学分析的准确性和科学性。