挡墙后土体应力状态与主动土压力计算分析
2022-05-17王雨波曹文贵
王雨波,曹文贵
(湖南大学 土木工程学院,湖南 长沙 410082)
挡土墙土压力问题一直都是土力学研究领域的一个重要内容,在经典理论中,朗肯理论(1857)由于假设条件过于理想而不能受到广泛应用,而库伦理论(1776)只能得到土压力合力却无法求得其分布,且库伦假设的土压力沿墙高为线性分布也无法得到国内外众多试验结果的支持[1-4]。土压力的分布形式是一个关键性问题,对土压力非线性分布的研究从土拱效应的发现和薄层微分方法的应用开始,取得了重大的进展。1943年,KARL[5]通过活动门实验证明了土拱效应的存在,将土拱效应描述为土体中应力的偏转和重分布,1985年,HANDY[6]将土拱定义为应力发生偏转后最小主应力的轨迹线,并推导其形状为悬链线,结合水平微分薄层受力平衡分析方法,求得了土压力的分布,分布解显示为非线性,良好地吻合了试验结果。此后众多的学者对该方法进行了改进,如PAIK等[7-8]分别将土拱形状假定为圆弧、抛物线等形状,根据水平薄层方法,得到了相应的土压力分布解;杨贵等[9-10]以曲线滑裂面为研究出发点,分别研究了在旋轮线和对数螺旋线滑裂面下的土压力分布;刘忠玉等[11]基于土拱效应,建立了考虑层间剪应力的土压力计算方法;张慧姐等[12]采用沿主应力迹线分层的研究方法,避免了剪应力对薄层受力分析的影响。土拱方法的基本思路是假定滑动土体整体所有单元处于极限平衡状态,即达到Mohr-Coulomb屈服条件,摩尔圆与抗剪强度线相切,据此先求出墙背上和滑裂面上主应力的偏转角,进而得到墙背处土压力强度与水平层平均竖向应力的比值系数(称为侧土压力系数),最后对水平薄层进行受力分析求解。然而,滑动土体完全达到极限状态的观点在近年来开始受到质疑。事实上,大部分情况下破坏单元仅出现在滑移面上,呈现整体滑动破坏的形式,而非整体式的“崩坏”,如文献[13]中的数值结果所示。刘洋等[14]认为,主动土压力状态下,墙面土体达到极限状态,而滑裂面上土体未达极限状态,原因是试验表明,在墙体背离土体运动过程中,墙土外摩擦角先于内摩擦角充分发挥,但这种条件下,滑裂面尚未形成,主动土压力还未达到稳定[13-15],因而文献[14]的解答实际上可看作一种非极限状态下的土压力解。当滑裂面出现时,主动土压力才达到稳定,因此,此时视滑移面上土体处于极限状态,而滑动土体内部及墙背土体单元处于非极限状态,会更加符合实际条件。另一方面,在运用土拱理论进行土压力分布的理论研究时,几乎都没有深究滑动土楔所受反力的分布,也没有考虑在相应土压力解答下,土楔能否满足整体的力矩平衡。茅以升[16]在1954年对库伦理论能否满足力矩平衡条件提出过质疑,但是在后续的土压力理论研究中,这个问题一直未能得到应有的重视。基于以上研究出发点,本文考虑滑裂面土体达到极限平衡状态,而土楔内部及墙面土体均未达到极限平衡状态,参考文献[14]中二维微分单元的研究方法和假设,得到主动土压力分布和土反力分布解,并进一步考虑土楔整体的静力平衡与力矩平衡条件,求解了滑裂面倾角及墙背土体非极限应力状态参数,建立了较为合理的主动土压力计算模型,并进行了验证分析。
1 微分方程的建立与求解
1.1 滑动土体微分方程
如图1所示的土压力计算模型,刚性挡土墙墙背竖直,墙后填筑无黏性土,填土面水平,土的重度为γ,内摩擦角为φ,墙高H,墙土摩擦角为δ,挡墙在墙后土体的推动下背离土体平动位移,直至滑裂面形成,土压力达到稳定,视为主动极限平衡状态。设该状态下土中滑移面近似为一通过墙踵的平面BC,滑裂面倾角为β。在墙踵处建立如图所示的平面直角坐标系,并取土楔中坐标为(x,z)的微元进行受力分析,根据弹性力学理论,可以得到微元体dxdz的平衡微分方程为
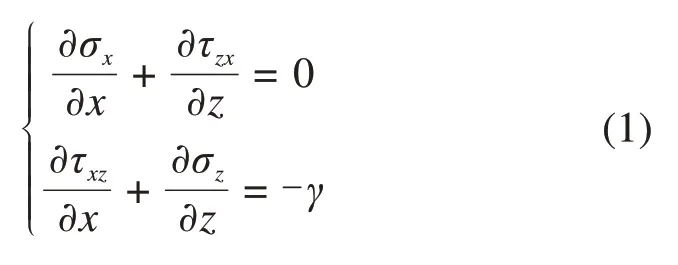
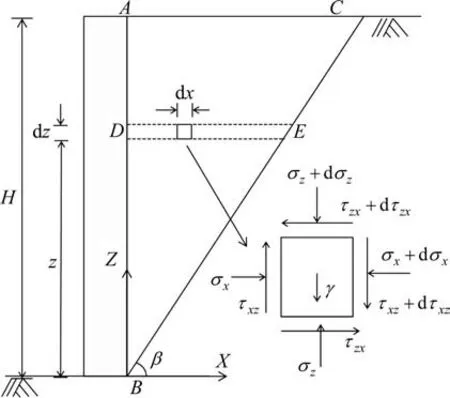
图1 主动土压力计算模型与微分单元Fig.1 Active earth pressure calculation model and differential element
1.2 边界条件
在滑裂面BC上,土体达到极限状态,其应力状态可由图2所示摩尔圆进行表示。其中,α是σ3与水平方向的夹角,σR是滑裂面上的法向应力。根据摩尔圆有如下关系
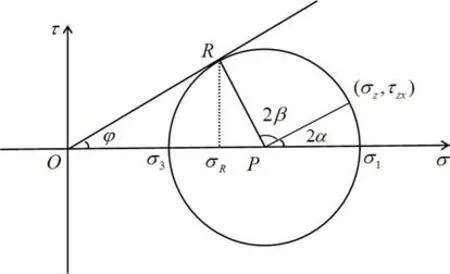
图2 滑裂面上土体单元的应力状态Fig.2 Stress state of soil element on sliding surface

在滑裂面上,定义剪应力与竖向应力的比值为B,则[14]
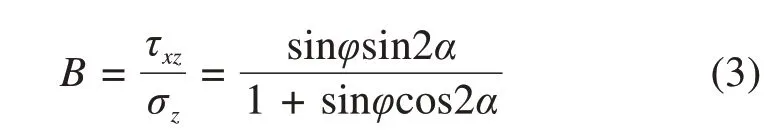
于是,滑裂面BC上的边界条件为
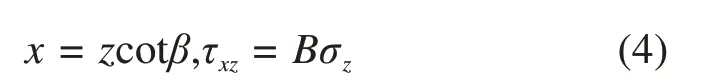
在墙面AB上,由于土体没有达到极限平衡状态,所以摩尔圆并不与抗剪强度线相切,如图3所示。本文用主应力比参数Km来对其状态进行描述,定义土体中任意一点的主应力比Km为

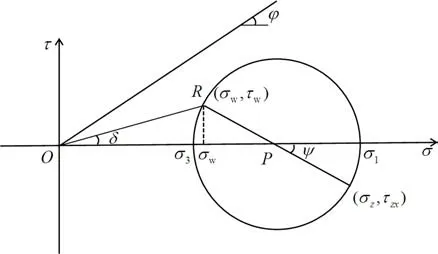
图3 墙背处土体单元的应力状态Fig.3 Stress state of soil element at the back of wall
显然,在极限状态下,Km=Ka,非极限状态下,Km>Ka。Ka为朗肯主动土压力系数,代表极限状态下最小与最大主应力之比,其值为

在图3中,σw和τw分别表示在挡土墙墙面上的正应力和切应力,在三角形POR中,根据正弦定理,有

其中,ψ表示σ3与水平面夹角的2倍角,于是
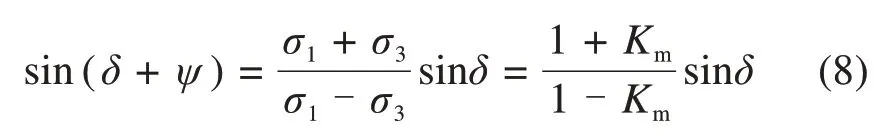
根据图3可进一步得到墙背处土体的σw和σz
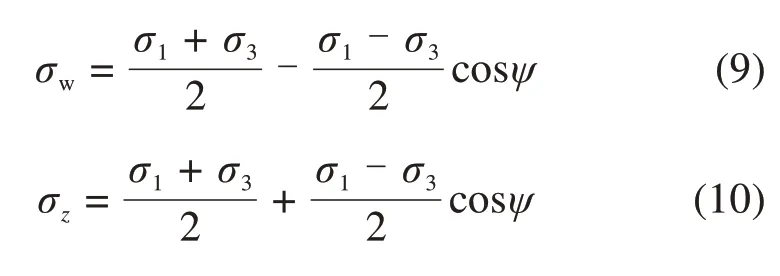
定义墙面处土的侧压力系数Kw为墙面上的正应力和墙面处σz的比值,即
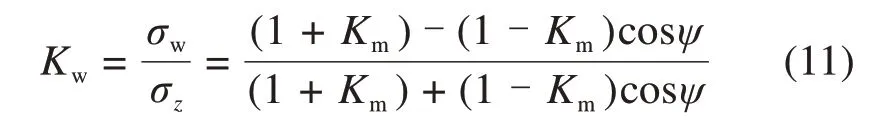
根据摩尔圆显然应有Kw>Km>Ka。这里,先将Km和Kw当做未知的参数来进行对待。定义比值
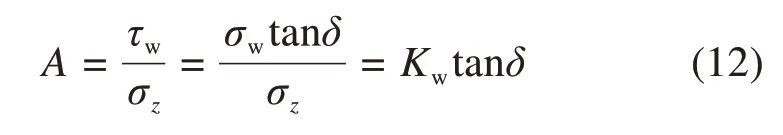
那么,墙背AB上的边界条件为

上边界AC条件为

1.3 土体的应力解
由于墙体位移很小,水平层面上的上覆应力变化不大,因此可将σz视作仅为深度的函数σz(z),结合边界条件可对微分方程进行求解[14],根据边界条件(4),(13),(14)可求得微分方程组(1)的应力解,从而得到σz和σw解答为
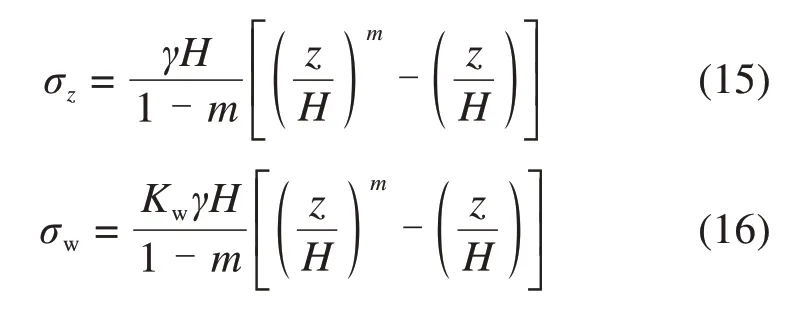
其中,

这里,土压力分布表达式(16)中含有未知的应力状态参数Kw,所以还需要通过其他条件对其状态进行确定。
2 非极限参数计算的力矩平衡方法
在图1所示的计算模型中,通过对土楔列整体静力平衡方程,可以得到主动土压力合力E和土反力合力R的大小分别为
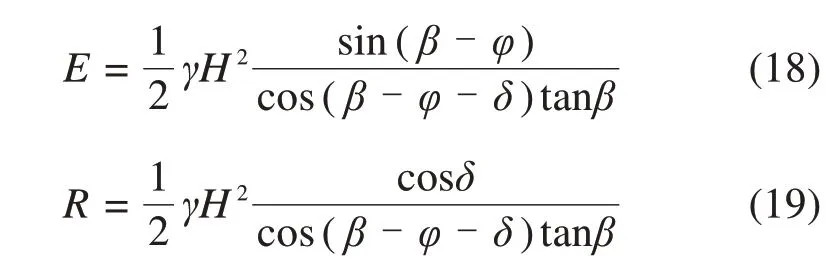
通过分布解式(16)积分求得的土压力合力为
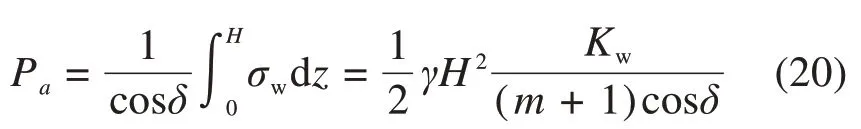
若将β大小当做已知,那么式(18)与式(20)应该相等,令式(18)等于式(20),于是可解得
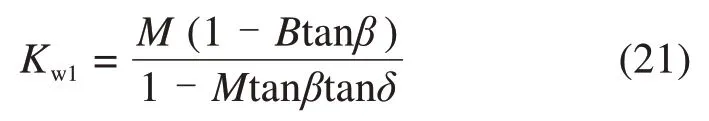
其中,

同样,土反力的合力R也应当要满足相等的条件。
根据图2,在滑裂面上有

令
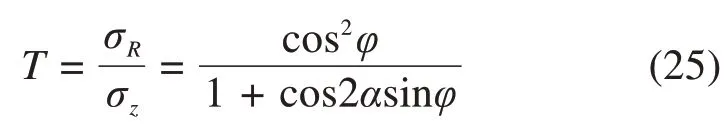
则
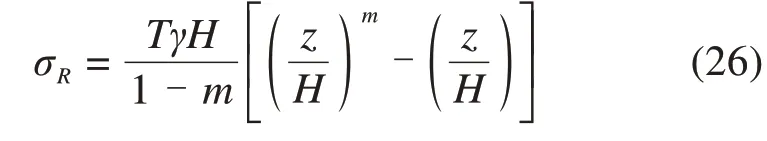
通过反力分布解(26)积分求出的反力的合力为
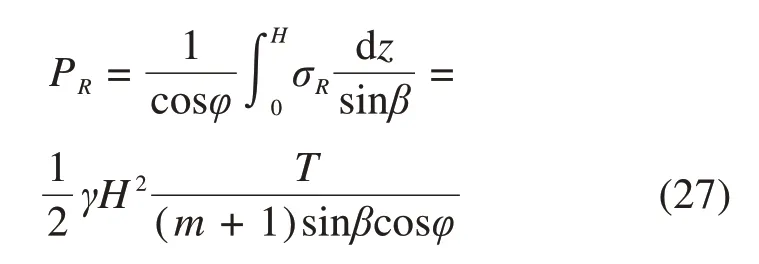
令式(19)与式(27)相等,解出Kw,可以验证得到和式(21)相同的结果。实际上,由于式(1)满足ABC中任一点的微观平衡条件,所以如果令土压力相等,那么土反力也必然是能够互相吻合的。但是力矩平衡条件却不一定能够满足,因为在这个问题中,边界BC和反力都是不确定的,这也是土压力问题不同于其他传统力学问题,一直以来成为疑难问题的重要原因,因为反力条件和内部应力条件都不是独立的已知条件,且紧密联系。这里,力矩平衡需要使滑移面BC满足一定的倾角条件,土楔ABC的力矩平衡方程为
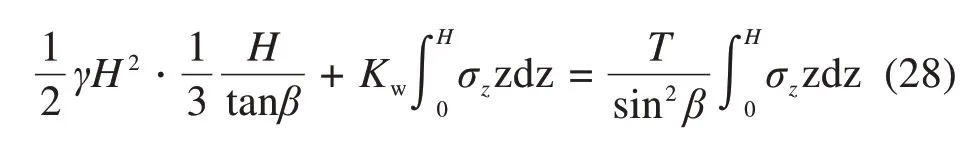
从式(28)中求解Kw,得到

令Kw1=Kw2,即可解出在定义范围内滑移面的倾角值β,由于难以解出显性表达式,可利用Mat‐lab进行数值求解该隐式方程。图4显示了在δ=φ/3时,不同理论方法所计算的滑移面倾角随内摩擦角φ变化的图像,从图中可以看出,不同方法所计算出的滑移面倾角都随内摩擦角φ的增大而增大,但在δ和φ相同的情况下,各方法所计算的β值中,库伦解最小,章瑞文等[17]的解较为接近且大于库伦解,而本文解最大,因此采用库伦滑裂面倾角可能会使土压力计算结果偏于保守。

图4 滑移面倾角计算值比较Fig.4 Comparison of calculated values of slip surface inclination angle
将从Kw1=Kw2所解得的倾角值用β0表示,再返回代入式(21)即可得到

由式(30)求解出侧土压力系数Kw之后,返回代入到式(8)和式(11)中,可以解得墙背处土体的偏转角ψ和主应力比Km。首先将式(11)进行如下变形
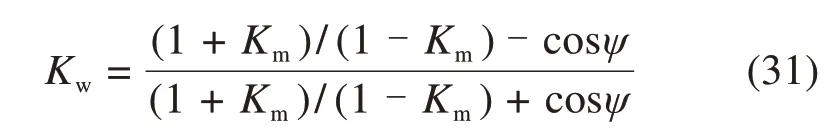
根据式(8)有

将式(32)代入式(31),得
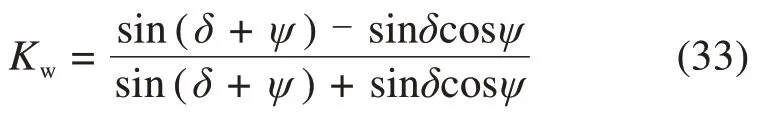
将式(33)进行三角变换并移项,解出
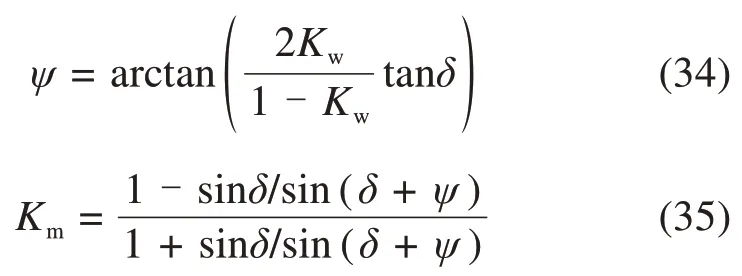
于是,墙面水平向主动土压力的分布解由式(16)给出,反力分布由式(26)给出,主动土压力合力为
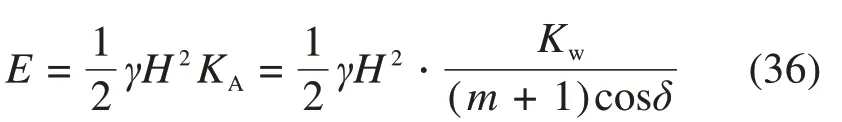
其中,KA为本文理论下的主动土压力系数。主动土压力合力作用点高度为

3 实例验证与参数分析
3.1 实例验证
为了验证本文理论的可靠性,采用文献[15]中编号342的平移模型试验(本文编号试验1)和文献[1]中砂性土模型试验(本文编号试验2)的实测数据,利用理论公式进行计算和对比分析。试验参数分别如下。试验1:φ=34°,δ=17°,H=1 m,γ=15.4 kN/m3;试验2:δ=21°,φ=34°,H=1.5 m,γ=12.56 kN/m3。试验结果和计算结果如图5所示。
从图5中可以看出,本文理论计算出的土压力分布与试验结果吻合良好,实测值点一直在本文理论曲线两侧波动,在土压力曲线峰值以上,相比于其他理论,本文理论解与实测值更为接近,各理论解答与实测值相差都不大,但在峰值以下,本文解则比实测值略偏小,而其余理论值均要明显大于实测值,其中paik解峰值强度与实测值偏差最大。本文理论解与试验结果随深度变化遵循着较为一致的变化规律。
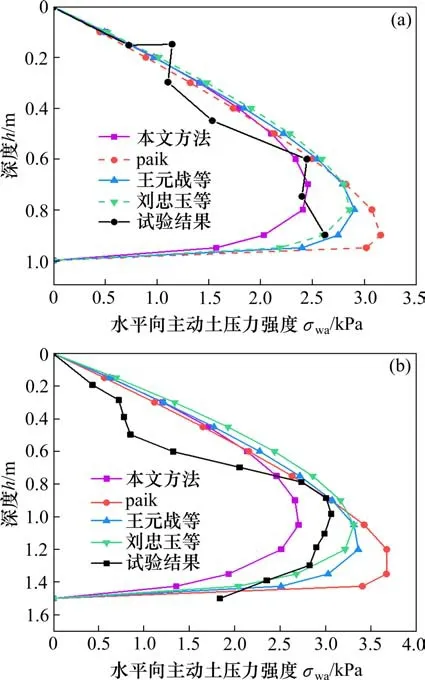
图5 主动土压力分布曲线对比Fig.5 Comparison of active earth pressure distribution curves
3.2 参数分析
根据本文理论公式,分别讨论内摩擦角φ和墙土外摩擦角δ对于土压力分布,合力作用点高度及应力参数的影响。
3.2.1 φ的影响
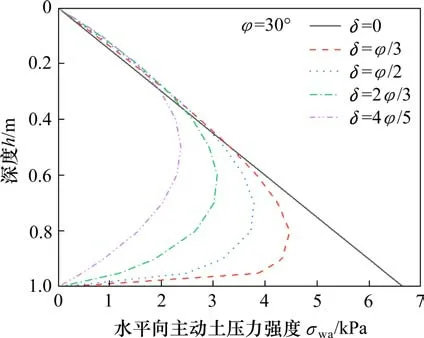
图6给出了γ=20 kN/m3,H=1 m,δ=φ/2条件下,主动土压力分布随φ的变化规律,从图中可以看出,当内摩擦角增大时,同一深度处的土压力值均变小,土压力合力明显减小,在土压力曲线的峰值点处减小值最大,峰值两侧减小值逐渐变小。从分布形状上看,土压力峰值出现的深度几乎不随内摩擦角的变化而变化,当内摩擦角增大时,土压力分布形状由尖锐而变得圆滑,非线性也越来越明显。
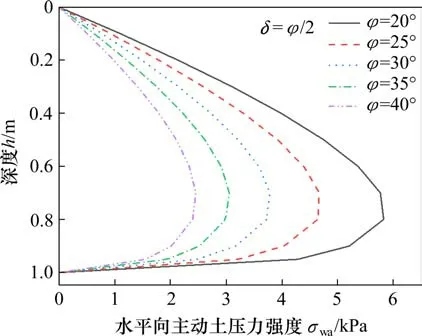
图6 内摩擦角对于土压力分布的影响Fig.6 Effect ofφon earth pressure distribution
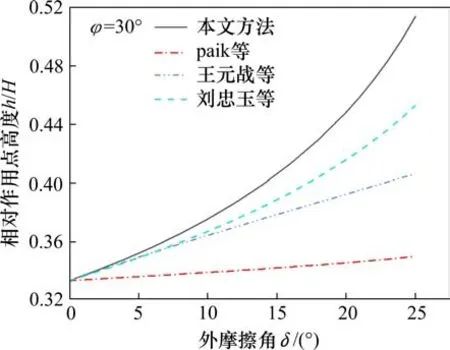
图7显示当δ一定时,φ的变化对于相对合力作用点高度h/H的影响。当φ取0时相对合力作用点位置均位于墙脚以上(1/3)点,随着内摩擦角的增大,合力作用点位置也逐渐增高,且δ越大,增高得越快。曲线的斜率随着φ的增大而逐渐减小,表明增长速率越来越慢,当φ=40°时,作用点高度不再随内摩擦角的增大而增加。无黏性土的内摩擦角一般不会超过40°,所以对于大于40°之后的情况不再进行讨论。
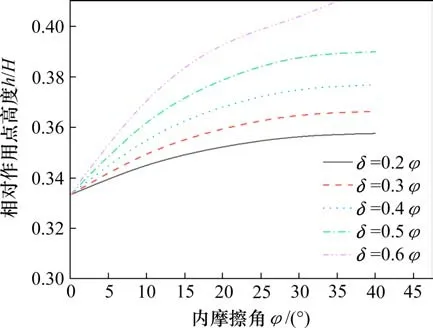
图7 内摩擦角对合力作用点位置的影响Fig.7 Effect ofφon position of resultant force action point
图8表明了内摩擦角φ对于侧土压力系数Kw的影响,Kw随φ的增大而逐渐减小,当φ一定时,δ越大,对应的侧土压力系数越大,但δ的取值对于Kw值却没有明显的影响,曲线之间彼此非常接近。图9表明了不同理论下的主动土压力系数Ka随内摩擦角φ的变化规律[7,11,18]。从图9可以看出,各理论均表明,Ka应随着φ的增大而减小。相比于其他理论,本文的主动土压力系数与库伦理论的主动土压力系数是最为接近的,这是因为本文方法考虑了滑楔体整体的静力平衡和力矩平衡条件,而其余理论是完全根据土拱效应和完全极限状态求得的结果。
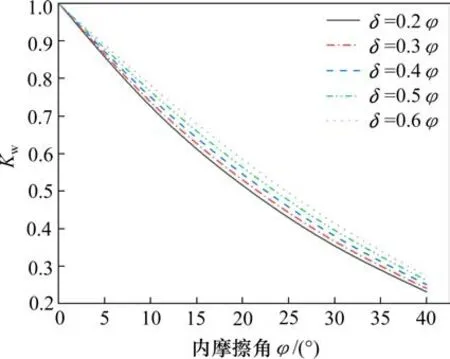
图8 内摩擦角对K w的影响Fig.8 Effect ofφon K w

图9 内摩擦角对土压力系数的影响Fig.9 Effect ofφon earth pressure coefficient
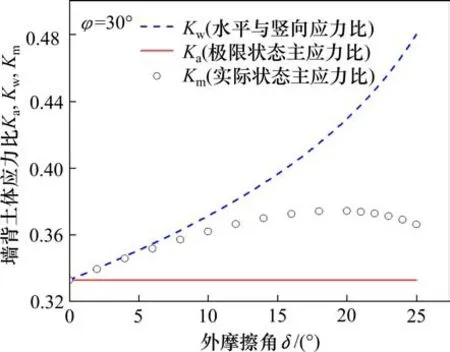
图10进一步展现了主动状态下的墙背侧土压力系数Kw,墙背土体的主应力比Km,以及朗肯主动土压力系数Ka三者间的大小关系。从图10可以看出,极限状态下的最小与最大主应力之比Ka最小,Kw最大,而Km位于二者之间,表明实际上墙背处土体由于没有达到极限状态,摩尔圆不与摩尔库伦抗剪强度线相切,因而Km>Ka,而在同一状态下,由于墙背处土体主应力发生了偏转,所以有Km 图10 墙背土体的应力状态参数比较Fig.10 Comparison of stress state parameters of soil behind wall 3.2.2 δ的影响 图11描述了土压力γ=20 kN/m3,H=1 m,φ=30°条件下,δ对于主动土压力分布的影响。从图中可以看出,随着内摩擦角的增大,土压力分布曲线首先由三角形(δ=0)变为梨形,而后整体形状逐渐向墙背收缩,非线性也越来越明显。在距离墙顶较浅深度范围内,外摩擦角变化对于土压力的大小影响很小,只有当深度接近于土压力峰值深度时,土压力大小才会对δ的变化变得十分敏感。总体上来讲,随着δ的增大,土压力合力明显减小,且峰值土压力深度逐渐增高。 图11 外摩擦角对土压力分布的影响Fig.11 Effect ofδon earth pressure distribution 图12展现了φ=30°条件下,合力相对作用点高度h/H随δ的变化规律,在不同文献的方法中,h/H均随着δ的增大而增大,增大的速率不同,paik理论中,h/H随着φ的增加而增大得很慢,而本文中,h/H随着φ的增加而增大得较快,作用点位置表现出对于外摩擦角变化较高的敏感性。 图12 外摩擦角对合力作用点位置的影响Fig.12 Effect ofδon position of resultant force acting point 图13显示了墙背土体的侧土压力系数Kw,主应力比Km,朗肯主动土压力系数Ka随δ的变化。在δ变化过程中,三者依然满足着Ka 图13 外摩擦角对应力状态参数的影响Fig.13 Effect ofδon stress state parameters 1)当挡墙背离土体移动,使得作用于墙背上的土压力减小并达到稳定时,作用于墙背上的土压力为主动土压力,此时土中有滑移面产生,滑移面上土体达到极限状态,而土楔内部土体及墙背处土体没有完全达到极限状态。 2)在不同内外摩擦角条件下,主动状态时墙背处土体的实际主应力比值Km与极限状态下主应力比值Ka非常接近,因此将其近似视作极限状态,采用土拱理论对土压力进行计算分析,不会对土压力计算结果产生显著影响。 3)计算平面滑移面倾角β大于库伦解和朗肯解。与土压力实测值相比,本文理论值在峰值点以上深度与实测值基本吻合,但在峰值点以下深度要略小于实测值。 4)随着φ的增大,土压力合力减小,作用点位置升高,主动土压力系数减小,墙背处土体的主应力比Km和侧土压力系数Kw也随之减小。随着δ的增大,土压力合力减小,作用点位置升高。δ不会对朗肯主动土压力系数Ka产生影响,但是会影响到墙背处土体的应力状态和主应力偏转角度。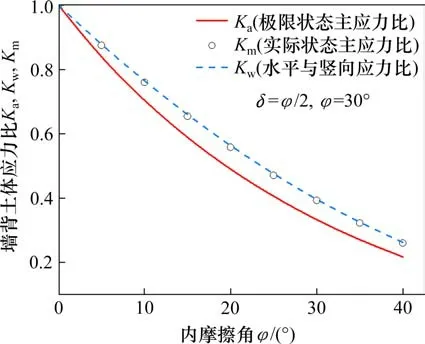
4 结论
