基于数据驱动的磁浮列车悬浮系统参数辨识

宋一锋，佟来生，倪菲，林国斌，梁涛

(1.同济大学 国家道路与交通工程教育部重点实验室，上海 201804；2.中车株洲电力机车有限公司，湖南 株洲 412001；3.同济大学 磁浮交通工程技术研究中心，上海 201804；4.中国铁建电气化局集团 第四工程有限公司，湖南 长沙 410007)

磁浮列车作为新兴的轨道交通运输方式，其最大的特点在于轮轨间无接触，利用车体的悬浮电磁铁与轨道表面电磁感应而产生的垂向悬浮力提供支撑[1]。由于列车运行过程中面临载重、不平顺等干扰，磁浮列车的悬浮间隙需要被实时控制在稳定范围内。其中悬浮系统起着间隙控制作用，通常在系统非线性模型基础上引入控制算法来调节输出电流，从而调节系统悬浮状态，因此系统模型作为悬浮控制的基础，其精确度影响着整个悬浮控制过程。常用的建模方法可分为基于模型的建模方法和基于数据的建模方法，如基于模型的有限元法通过对真实物理系统进行模拟，得到精确模型，但结果形式复杂，不便于应用在实际工程中。而基于数据的建模方法实现过程较为便捷，可分为2类：一类是应用智能算法对系统的输入输出关系进行辨识，根据系统变量历史数据学习变量之间的逻辑关联，常见的有神经网络、贝叶斯算法或模糊关系等，由于该建模过程未涉及系统自身的物理特征，因而所建立的模型可解释性较低；另一类是应用算法对系统模型进行参数辨识，在多数情况下，系统的物理机理明确，但由于外部干扰等不确定因素，难以建立精确的数学模型，于是结合系统运行过程数据对物理参数进行辨识，通过挖掘数据统计特征来估计参数值，经典方法为最小二乘法，随后根据优化原理发展的算法有遗传算法、粒子群算法等[2-3]。磁浮列车悬浮系统模型具有本征非线性，为便于分析，常用做法是对非线性控制系统在平衡点处进行泰勒展开，得到线性模型。但是线性化处理会丢失非线性特征，产生系统偏差[4]。利用线性模型设计的悬浮控制算法，仅能使系统在微小干扰下保持平衡，当系统输出出现较大误差时，控制算法难以及时调节而发生运行故障[5-6]。因此，很多学者关注如何建立非线性模型及参数辨识，以便提高系统控制性能。CHEN等[7]采用Hopfield神经网络对悬浮系统非线性项进行参数辨识，并结合径向基函数设计控制律，提高了控制精度。刘恒坤等[8]通过对悬浮系统的电流环进行降阶处理，采用最小二乘法对系统三阶模型进行参数辨识。孙友刚等[9]通过建立悬浮系统非线性模型，在此基础上设计滑模控制律，利用整车试验验证算法有效性。CHEN等[10]建立磁浮列车−轨道非线性耦合模型，并根据RBF网络逼近原理来设计自适应控制器，以提高控制的鲁棒性。胡国良等[11]结合粒子群算法和最小二乘法对磁流变阻尼器的Bouc-Wen非线性模型进行参数辨识，并验证了辨识结果的准确性。为对悬浮系统建立准确的非线性模型，本文采用一类生物优化算法——基于线性递减惯性权重的粒子群算法对系统的悬浮物质量、磁极面积和线圈匝数等参数进行参数辨识，结合励磁电流、悬浮间隙和垂向加速度等系统变量的闭环过程数据，以实测值与计算值的均方误差为目标函数，通过粒子寻优得到使误差最小的全局最优解。并与非线性最小二乘法相比，该方法的参数辨识误差更小。

1 磁浮列车悬浮系统模型

悬浮控制系统作为磁浮交通系统的关键子系统，决定列车运行的安全性与平稳性。如图1所示为磁浮列车运行示意图。磁浮交通系统由磁浮列车、轨道与桥梁3部分构成，其中悬浮系统作用于车体与轨道之间，通过车体中悬浮架上的电磁铁与轨道表面发生电磁感应作用，能够对车体产生向上的悬浮力[10]。悬浮控制器根据实际运行状态实时调节悬浮力的大小，从而实现列车的平稳运行。

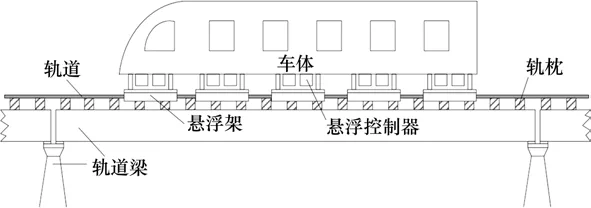
图1 磁浮列车运行示意图Fig.1 Schematic diagram of maglev train

磁浮列车由若干个悬浮架支撑，每个悬浮架由4个悬浮点组成，车的两侧各为2个。根据悬浮架的解耦分析，磁浮列车悬浮控制系统可视为多个独立的单点悬浮控制系统。单点悬浮系统模型如图2所示，图中，m为车体质量，ze为期望间隙，z为当前悬浮间隙，z̈为间隙变化加速度，i为励磁电流，A为单电磁铁磁极面积，N为线圈匝数，Fl为垂向悬浮力，μ0为真空磁导率。

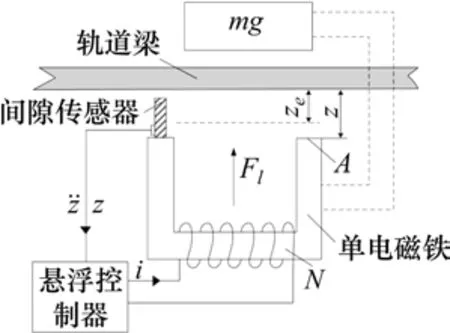
图2 单点悬浮系统模型Fig.2 Model of single-point levitation system

电磁铁采用电流励磁方式，与轨道梁的金属表面构成磁力线回路，假设磁路在气隙中未发生漏磁，磁场均匀分布，且磁路的磁极面积始终为定值，电磁悬浮力可以表示为：

向上的悬浮力作用于车体与电磁铁连通的悬浮架上，根据牛顿定律，单点悬浮系统2阶数学模型可以表示为：

由式(2)可知，悬浮力与电流i，间隙z存在非线性关系。当悬浮间隙z越大，所产生的悬浮力越小，当悬浮力小到无以支撑车体的重量时，会发生悬浮失稳或砸轨现象，由此可得，悬浮系统本身为开环非自稳系统，需要反馈控制环节来动态调整悬浮间隙，使其稳定于期望值附近。

图2中，悬浮控制器起着反馈控制作用，通过间隙传感器获取当前悬浮间隙与间隙变化加速度，结合反馈控制律，得到合适的励磁电流，从而实时调节悬浮力的大小，使悬浮间隙处于期望范围内。

2 基于数据驱动的悬浮系统参数辨识方法

在系统辨识和参数估计领域中，最小二乘法作为一种最基本的估计方法应用极为广泛。由式(2)可知，悬浮系统数学模型是非线性的，可测变量为悬浮间隙z，间隙变化加速度z̈和励磁电流i，待辨识参数有线圈匝数N，磁极面积A和悬浮物质量m。为展开最小二乘估计，将非线性模型式(2)转化为线性回归方程结构：

其中：

由式(5)可知，当HTn H n可逆时才有解，因此最小二乘估计结果易出现奇异解，应用于多阶非线性系统时具有局限性。

与这类求特定解的确定性算法相比，一类生物优化算法通过模仿自然现象来搜索解空间。其中粒子群算法通过模拟鸟群觅食行为来寻优，基于多智能体之间的信息传递迭代搜索全局最优解，因此收敛速度较快。并且算法本身结构简单，需要调节的参数较少，广泛应用于工程实践。

粒子群算法流程图如图3所示。首先进行参数初始化，设定最大迭代次数Gen和种群规模Size，并产生一组随机解，以基于均方根误差的目标函数来评判个体适应值，当均方根误差达到最小时，得到初始的全局最优值。目标函数可以表示为：

图3 粒子群算法流程图Fig.3 Flow chart of particle swarm optimization

式中：n代表数据观测长度；Xk代表第k个实测值；代表相应的估计值。为对悬浮控制系统进行参数辨识，考虑Xk代表系统输出间隙zk，其相应估计量可以计算为：

式中：ik，分别为电流和间隙加速度的第k次实测值，μ0N2A/m为待辨识参数，p di(i=1,2,…,Size，d=1,2,…,Gen)为某个粒子个体，代表一组可能的参数解。

在粒子群算法中，引入局部自适应变异算子来更新粒子p di的位置，即通过学习自身与个体最优解、局部最优解的差异来调整速度与位置：

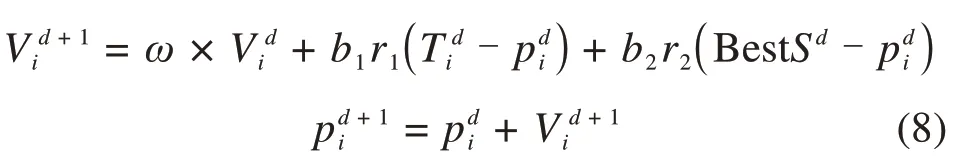
式中：V d i为第d次迭代的速度；V d+1i为第d+1次迭代的速度；ω为惯性权重；T d i为第d次迭代第i个粒子的个体最优解；BestSd为第d次迭代的全局最优解；p d+1i为更新后的粒子；b1为局部学习因子；b2为全局学习因子；r1和r2为(0,1)之间均匀分布的随机数。

多次迭代过程中，在继承个体最优解与全局最优解的基础上进行变异与粒子的更新来达到寻优的目的，当满足迭代终止条件时得到全局最优解。但基本的粒子群算法容易陷入局部最优解，为避免这一现象，采用线性递减惯性权重来调整速度更新步长：

式中：ωmax和ωmin分别为惯性权重的上下限，ωd为每次迭代的权值，由式(9)可知，算法在初始时具有良好的全局搜索能力，逐步逼近全局最优解的区域，后期随着搜索步长减小局部搜索性能提高。

3 数值仿真及实验

3.1 数据采集

为获取悬浮系统电流、悬浮间隙和间隙变化加速度等时变数据，建立实时仿真系统DSPACE与单点悬浮试验台的半实物联合仿真系统，如图4所示，该系统由悬浮试验台、悬浮控制器、接口变换板和DSPACE等关键设备组成。其中悬浮控制器与式(2)所示的开环非自稳系统构成闭环回路，本文选用经典的PID控制律对系统展开反馈控制：

图4 DSPACE与单点悬浮试验台的半实物联合仿真系统Fig.4 Hardware-in-the-loop simulation system based on DSPACEand single-point levitation test-bed

式中：kp，ki和kd为反馈控制参数；i0(t)为系统动态平衡过程的控制电流。

在系统运作中，悬浮试验台的输入电流值保持在26.5 A左右，实施辨识试验时，在悬浮控制器输出的控制电流基础上施加正弦激励信号，由DSPACE数据采集设备监测悬浮试验台的输入电流，图5分别展示了正常情况下和正弦激励时的控制电流。取图5(b)中10~40 s持续且稳定的悬浮过程数据为试验数据。采样频率设为1 000。

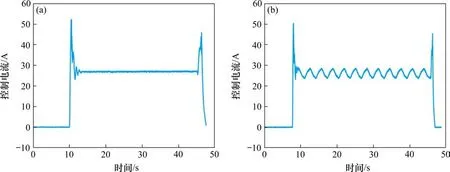
图5 悬浮试验台的控制电流Fig.5 Control current of levitation test-bed

3.2 参数辨识结果

所采集的电流I，悬浮间隙z和垂向加速度z̈的闭环过程数据分别构成长度为3 000的一维数组，将其代入式(4)中，并采用式(5)计算结果为：θ̂=[9.882 8×10-42.887 3×10-32.887 3×10-3]，则最小二乘法的参数辨识结果为：μ0N2A/m=3.906 8×10-6。

为与该辨识算法形成对比，应用粒子群优化算法进行参数辨识。设置种群规模为20，迭代次数为100，局部学习因子与全局学习因子均为2.05，惯性权重在(0.1,0.9)之间线性递减。根据图3所示的粒子群算法流程，在Matlab平台迭代计算得到的辨识结果为：μ0N2A/m=5.855 2×10-6。目标函数J的优化过程如图6所示，最终的辨识误差指标为0.162。

图6 目标函数J的优化过程Fig.6 Optimization process of objective function J

4 辨识参数的验证

为验证参数辨识结果的有效性，根据辨识的物理参数值，结合式(4)和式(10)在Simulink平台建立非线性悬浮系统的反馈控制仿真模型，通过仿真模型模拟真实的悬浮试验台，并将模型输出序列与实测序列作对比来进行辨识参数的验证。反馈控制框图如图7所示，图中，控制算法及控制参数与悬浮试验台(图4所示)所使用的一致，其中反馈控制参数kp=25 000，ki=100，kd=800。正弦激励信号仍为图5(b)中试验台的控制电流，目标间隙值为0.01 mm。

图7 反馈控制框图Fig.7 Feedback control block diagram

分别将最小二乘法和粒子群算法得到的辨识结果代入仿真模型，得到相应的输出结果，其与悬浮试验台输出间隙实测值的对比如图8所示。

图8 间隙实测值与仿真结果Fig.8 Measured and simulation resultsof gap

由图8可知，粒子群算法对应的输出间隙的稳态误差相较于最小二乘法对应的误差更小，其与实测序列均围绕0.01 mm的水平线振动，说明粒子群算法的参数辨识结果更贴近真实值，验证了辨识结果μ0N2A/m=5.855 2×10-6的准确性。但其振动幅值比实测序列的小很多，可视为仿真模型忽略试验台的弹簧系统而引起的振动偏差。

5 结论

1)以中低速单点悬浮试验台为研究对象，结合DSPACE动态仿真系统搭建半实物联合仿真平台，监测得到关于悬浮间隙、垂向加速度和励磁电流的闭环过程数据。

2)以实测值与估计值的均方根误差为优化目标，采用粒子群优化算法对试验台悬浮物质量、线圈匝数和磁极面积等参数进行辨识，通过寻优迭代得到全局最优解为μ0N2A/m=5.855 2×10-6，此时辨识误差指标为0.162。此外，采用最小二乘法对该非线性系统辨识，得到的辨识结果为μ0N2A/m=3.906 8×10-6。

3)为验证辨识结果的有效性，分别引入2种算法的辨识结果，搭建悬浮系统仿真平台，并采用与悬浮试验台相同的控制算法及控制参数，达到模拟试验台控制过程的效果。

4)通过对比，采用粒子群算法所得辨识结果的系统输出间隙更贴近实测间隙序列的特征，说明粒子群算法所得结果更为准确。该结果也为悬浮系统动力学响应分析提供可靠的理论基础，并且基于数据驱动的粒子群优化辨识方案对于修正非线性模型具有现实意义。