基于LMD-TCN的高铁沿线风速观测资料质量控制算法研究

叶星瑜，叶小岭，马伟叁，熊雄，陈昕，袁诗云

(1.南京信息工程大学 气象灾害预报预警与评估协同创新中心，江苏 南京 210044；2.南京信息工程大学 江苏省大气环境与装备技术协同创新中心，江苏 南京 210044；3.中国铁路上海局集团有限公司，上海 200071)

大风是影响高铁安全运行的主要气象灾害之一，当列车遭遇较大环境风速时，极易导致列车脱轨或者倾覆[1]。为保证高铁的运行安全，需监测高铁沿线风速观测资料，在大风频发区域设置防风墙，并对高速铁路沿线大风实现提前预报预警[2-3]。风速观测资料在采集和传输的过程中易受到各种误差的干扰，而数据的质量在一定程度上会影响高铁能否安全运行的评估，因此对高铁沿线风速观测资料质量控制的研究具有重要的实用意义和理论研究价值。气象观测资料质量控制方法由单站质量控制和多站质量控制2部分组成。单站质量控制从数据的时间维度分析：JIMÉNEZ等[4]从极值检查、时间一致性检查和时间序列均质化等角度对风速、风向的质量进行评估；李娟[5]以气象要素的时间相关性为基础，将相空间重构(PSR)和支持向量机方法(SVM)结合，实现对气象要素的质量控制；杨洋[6]利用长短期记忆神经网络(LSTM)检测并插补温度数据中的异常值；YUAN等[7]通过百分位廓线值计算气候学界限值实现对髙频探空温度和风速的质量控制。多站质量控制从数据的空间维度分析：YE等[8]考虑到现有质量控制方法在多个时间尺度和不同地区上的局限性，提出了一种基于自适应算法和粒子群算法的改进核回归(IKR)算法；熊雄等[9]针对反距离加权法(IDW)和空间回归方法(SRT)的不足，提出了一种融合SRT和B样条拟合的地面气温资料质量控制方法；井高飞等[10]采用空间一致性和观测一致性相结合的方法，对地面自动雨量观测资料进行质量控制。由上述可知，风速观测资料质量控制算法的研究大多数仍停留在传统的质量控制算法层面。本文针对风速序列非稳定性和非线性的特征，构建了一种基于局部均值分解法(Local Mean Decomposition，LMD)和时间卷积网络法(Temporal Convolutional Network，TCN)的混合模型，将其引入到质量控制中，形成一种检错率高、适应性强、适用于高铁沿线的单站风速观测资料质量控制算法——LMDTCN质量控制算法。

1 数据

本文选用我国京沪高铁沿线江苏段气象观测站的风速数据，选择其中4个具有不同地理环境的站点作为目标站进行研究，包括南京大胜关长江大桥站(站号：K1005)、南京南站(站号：K1021)、句容市邹王路站(站号：K1066)和阳澄湖西桥站(站号：K1256)。考虑到风速观测资料在时间尺度上的完整性，选择4个目标站的2018年逐秒风速观测资料进行质量控制研究，上述数据均已经过基本的质量控制，明显粗大误差被剔除，能够准确描述风速观测资料的特征。

为检验质量控制算法的可行性，本文采用HUBBARD等[11]提出的人为误差插入法，在目标站的原始观测资料中植入3%的随机误差，再根据质量控制算法求得的预测值与插入随机误差后的观测值进行比对，得到该算法的检错率。插入随机值的大小通过公式(1)产生。

其中：p是服从区间[-m,m]，以0为均值的随机数；m为大于0的常数；s是目标站观测资料的标准差；x为误差插入的位置。

2 方法

2.1 局部均值分解

局部均值分解(LMD)[12]是SMITH提出的一种新的非线性非平稳信号分析方法，以信号的局部极值特征为出发点，将信号自适应地分解成一系列具有实际物理意义的乘积函数之和。利用LMD对风速时间序列x(t)分解，得到k个PF分量和1个残余分量uk(t)，分解结果如式(2)所示。

2.2 时间卷积网络

时间卷积网络(TCN)是将卷积神经网络应用于处理时间序列数据的一种新方法。时间卷积网络的结构可分为因果卷积、膨胀卷积和残差模块3部分。因果卷积通过对卷积滑动窗口的限制，保证未来的数据不被用来预测[13]。膨胀卷积的卷积核中具有空洞，可增大神经元的感受野，从而引入更多的历史信息。膨胀卷积的计算公式为

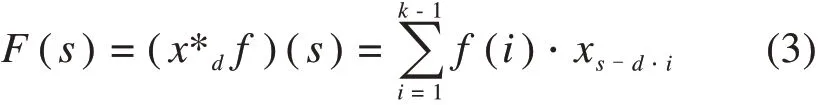
式中：k为卷积核大小；d为膨胀因子；*为卷积运算符。

残差模块在一定程度上消除了深度网络部分梯度消失和爆炸的影响，残差模块中跨层链接的恒等映射实现了神经网络的跨层传递信息，使时间卷积网络结构更具有泛化能力。

时间卷积网络兼具了循环神经网络[14]和卷积神经网络[15]的优点，不仅可以记忆前后时刻信息，而且具有运行效率高和可堆叠网络层数深的优点。

2.3 LMD-TCN质量控制算法

风速时间序列具有非平稳性、非线性的特征，故本文首先运用LMD方法将原始风速时间序列分解，然后通过TCN分别建立模型，最后将输出结果叠加得到目标站的预测值，与目标站观测值对比，若两者之间的差值超出阈值，则将其标记为可疑值。具体实现过程如下：

第1步，选取目标站的风速时间序列x(t),t=1,2,…,T；

第2步，利用LMD对x(t),t=1,2,…,T分解，得到k个PF分量和1个残余分量uk(t)，分解得到的k+1个分量非平稳性降低；

第3步，对分解得到的分量分别建立TCN模型，利用网格搜索对模型的超参数进行寻优，得到最佳的预测模型；

第4步，将各分量预测的结果叠加，得到目标站的预测值；

第5步，利用评价指标来评估所构建模型的预测精度；

第6步，将LMD-TCN方法得到的预测值Test(i)与插入随机误差后的观测值T′obs(i)对比，若两者之间的差值不满足式(4)，则认为数据为可疑值。

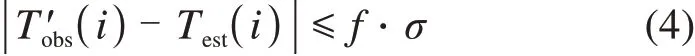
其中：f为质控参数；σ为观测值的标准差。

LMD-TCN质量控制算法具体流程图如图1所示。

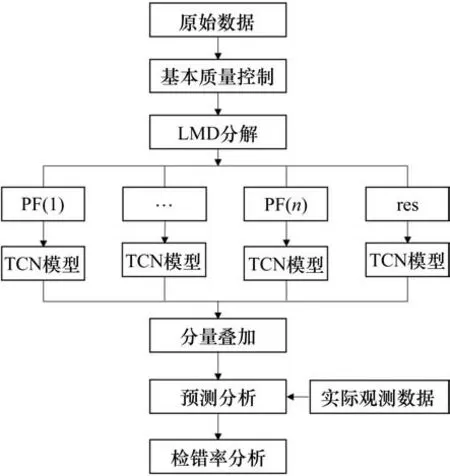
图1 LMD-TCN算法流程图Fig.1 Flow chart of LMD-TCN algorithm

2.4 评价指标

评价模型预测精度的指标有平均绝对误差(Mean Absolute Error,MAE)、均方根误差(Root Mean Square Error,RMSE)与纳什效率系数(Nash-Sutcliffe Model Efficiency Coefficient,NSC)。其中，RMSE用于衡量观测值与预测值之间的偏差，MAE表示观测值与预测值之间绝对误差的平均值，两者均为大于0的常数，数值越接近0，表明模型的性能越好；NSC用于衡量模型预测结果的好坏，为介于0～1之间的常数，数值越接近1，表明模型的拟合效果越好。

3 试验设置

3.1 对比试验设置

选取京沪高铁沿线江苏段的K1005，K1021，K1066和K1256作为目标站，利用LMD-TCN算法对风速观测资料进行预测，以RMSE，MAE和NSC 3项指标评估预测效果。同时，为证明LMDTCN质量控制算法的可靠性与普适性，将其与传统的时间卷积网络法(TCN)、长短期记忆神经网络法(LSTM)以及支持向量回归法(SVR)对比，分析其预测精度与检错效果。

3.2 参数设置

时间卷积网络中的卷积核大小、卷积核个数、舍弃率以及膨胀系数的设置对模型结果有至关重要的影响。对于京沪高铁沿线的4个站点，时间卷积网络中超参数的设置有所不同，本文通过超参数优化中的网格搜索确定时间卷积网络模型的超参数。表1为不同超参数的取值范围。

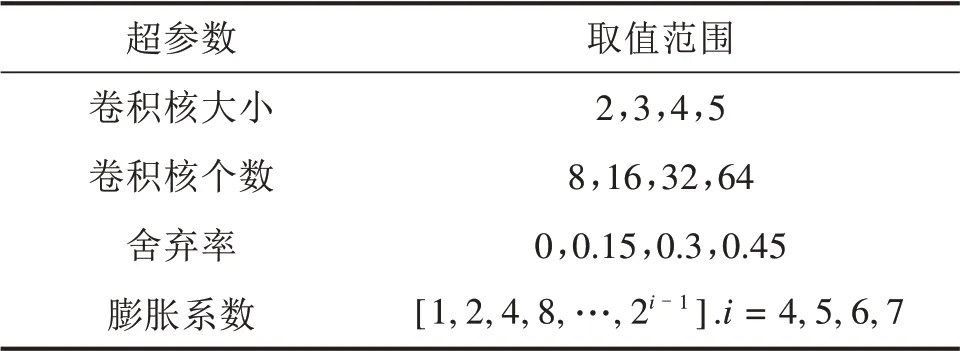
表1 超参数取值范围Table 1 Hyperparameters range

以南京大胜关大桥站为例，网格搜索得到的TCN模型的超参数为：卷积核大小设置为3；卷积核个数设置为64；舍弃率设置为0.45，防止模型过拟合；膨胀系数设置为[1,2,4,8,16,32,64]。模型初始学习率设置为4，每经过一定的训练次数，学习率会衰减为原来的50%，直至模型收敛。

4 试验结果及分析

针对高铁沿线风速观测资料非稳定性的特征，构建一种基于局部均值分解法(LMD)和时间卷积网络法(TCN)的高铁沿线风速观测资料质量控制算法——LMD-TCN算法。首先利用LMD方法对京沪高铁沿线江苏段选取的目标站2018年逐秒风速观测资料进行分解。风速时间序列经过分解之后，可以削弱非平稳性对预测精度的影响，然后利用TCN分别建立非线性模型并将输出结果叠加得到最终风速预测值，与目标站观测值对比达到质量控制的目的。

4.1 预测结果对比

以南京大胜关长江大桥站为例，分析LMDTCN算法的预测结果，为了便于观察预测值与实际观测值的对比结果，本文仅截取其中一部分预测结果作图。

图2为4种不同算法预测值与真实值的对比。由图2可得知，LMD-TCN算法预测值与实际值在波峰和波谷处与实际观测值略有偏差，其余部分基本吻合，拟合效果好；TCN算法与LSTM算法预测结果相近，整体来说TCN算法略好；SVR算法预测值在波峰波谷处偏离较多，预测结果差。由此可见，LMD-TCN算法的预测效果优异，预测得到的风速数据能够反映风速的实际变化规律。

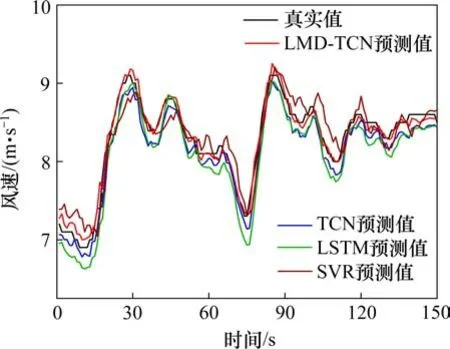
图2 预测结果对比Fig.2 Comparison of prediction results

4.2 可靠性分析

本文涉及的质量控制算法包括2部分内容：对目标站风速观测资料的预测及其与目标站实际风速观测资料的对比。这2个部分的结果共同影响质量控制的效果：算法的预测精度越高，预测值Test(i)越接近风速的实际变化规律，对观测值Tobs(i)的质量控制效果越具有说服力；预测值Test(i)在一定的误差范围内可以代表风速的实际变化规律，将其与插入随机误差的目标站的观测值T′obs(i)对比，检测原始数据中是否存在错误数据。所以，本文从算法的预测精度分析和检错效果分析对LMD-TCN算法的可靠性进行分析。

4.3 预测精度分析

图3为LMD-TCN方法在2018年4个站点在不同季节的RMSE和MAE指标对比结果，表2为NSC指标对比结果。从图3中可以看出，对于不同地区不同季节，LMD-TCN方法的RMSE指标均小于0.15，MAE指标均小于0.11，具有较高的预测精度。虽然4个站点均属于亚热带季风气候，但受局部小气候的影响，4个不同站点在不同季节的预测精度变化情况有所不同。K1005夏季RMSE和MAE指标略高，其原因是南京大胜关长江大桥夏季强风天气多，风速波动较大。K1021秋季的RMSE和MAE指标略低，其原因是南京南站属于北亚热带季风气候，风速呈现“春季大，秋季小”的分布。K1066冬季的RMSE和MAE指标最高，其次是春季和夏季，其原因是该站点冬季冷空气活动频繁常伴有大风天，春季冷空气过境引起大风，夏季因台风影响风速波动较大。K1256冬季和春季的RMSE和MAE指标较高，其原因是该站点冬季受冷气团影响产生寒潮大风等天气，春季依旧受到冬季大气环流的影响易出现强风和大风天气。由表2可知，LMD-TCN方法在不同站点的不同季节NSC指标均接近于1，表明该方法具有较好的拟合效果。

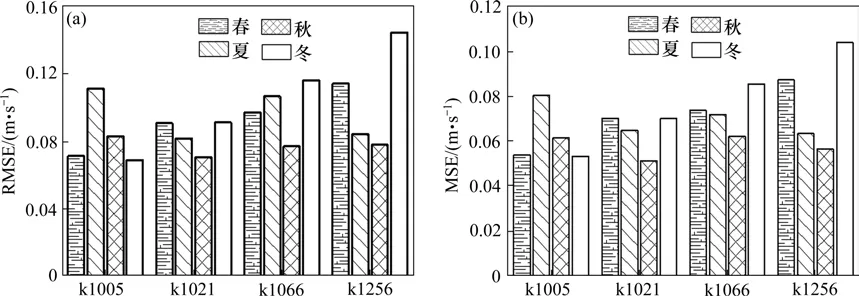
图3 在不同站点不同预测指标对比Fig.3 Comparison of different forecast indexes at different stations

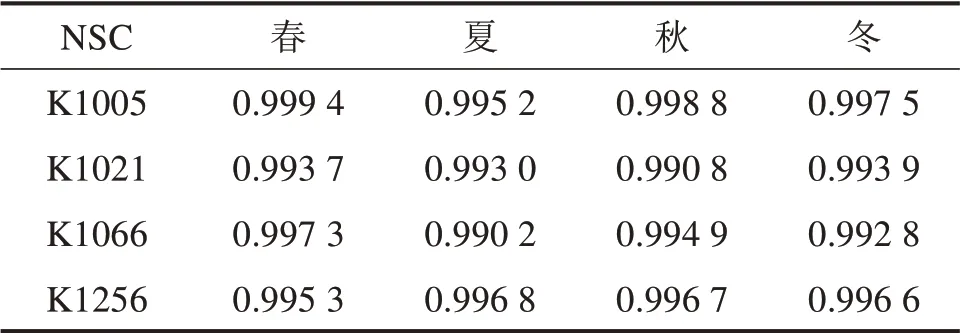
表2 不同站点NSC指标对比Table 2 Comparison of NSCat different stations

图4为不同方法在南京大胜关长江大桥站2018年不同季节的RMSE和MAE指标对比结果，表3为NSC指标对比结果。从中可以明显看出，LMDTCN方法的3项指标均好于TCN，LSTM和SVR方法。在不同的季节，LMD-TCN方法的预测性能具有明显的优越性，拟合效果也优于其他3种方法。4种方法在南京大胜关长江大桥站夏季的预测精度较低且拟合效果略差，其原因是该站点受沿西北向移动的台风影响，夏季多台风天气。LMDTCN方法在不同季节的RMSE指标在0.07左右，MAE指标在0.08左右，表明了该方法的稳定性。4种方法在南京大胜关长江大桥站2018年不同季节的预测效果总体来说由好及次依次是：LMD-TCN>TCN>LSTM>SVR。

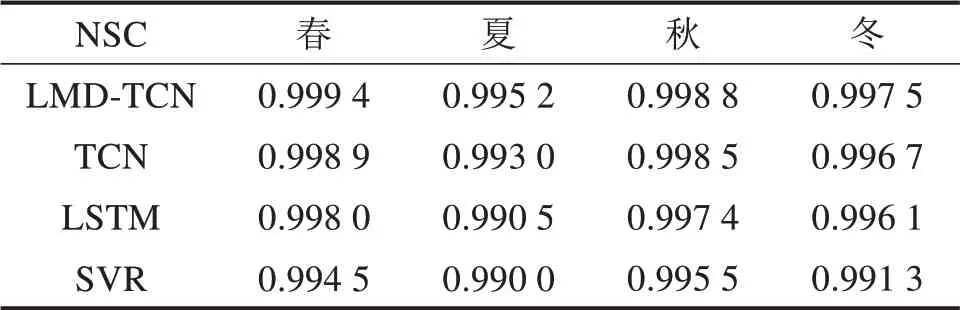
表3 不同方法NSC指标对比Table 3 Comparison of NSCwith different methods

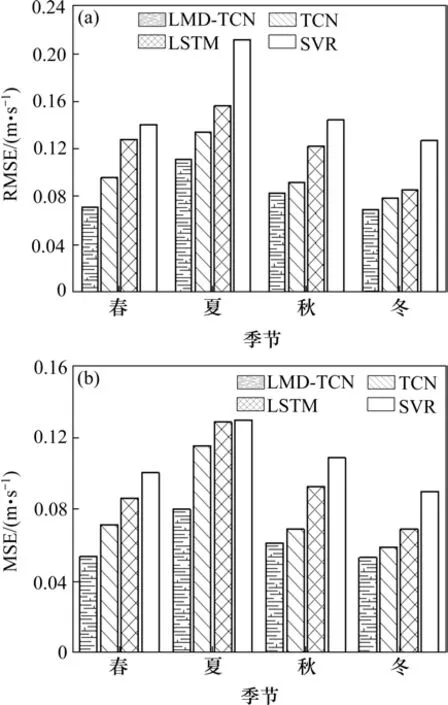
图4 不同方法不同预测指标对比Fig.4 Comparison of prediction indexes with different methods

4.4 检错效果分析

在目标站的观测值中插入3%的随机误差，并与预测值对比，得到第1类错误、第2类错误以及检错率，分析质量控制算法的检错效果。在控制统计学中，当第1类错误“弃真”和第2类错误“纳伪”差距最小时，此时的f值为最优质控参数，对应的检错率为最优检错率。

为了研究质控参数f的取值差异对检错率的影响，利用LMD-TCN方法对南京大胜关长江大桥站2018年不同季节风速观测资料进行质量控制，质控参数f取不同的值时，2类错误的概率与质控参数f变化关系如图5所示。随着质控参数f的增大，第1类错误的概率迅速减小，第2类错误的概率缓慢增大，检错率缓慢降低。由图5可知，不同季节的最佳质控参数f基本在0.06～0.16之间，相应最佳的检错率均在0.9以上，一方面表明不同季节最佳质控参数f的选取存在差异，需依据具体情况选取不同的质控参数f进行质量控制，另一方面表明LMD-TCN质量控制算法误差识别率高。

为了证明LMD-TCN质量控制算法的普适性，运用LMD-TCN，TCN，LSTM及SVR方法分别对K1005，K1021，K1066和K1256 4个不同站点2018年风速数据进行质量控制，检错结果如图6所示，其中箱线图中的黑点表示算法在不同站点检错率的均值，上下2条线分别表示检错率的最大值和最小值。从图6中可以看出，SVR方法的检错率与LMD-TCN，TCN和LSTM这3种方法相比变化范围大，稳定性较差。对于不同的站点，LMDTCN方法的检错率在0.965左右，TCN和LSTM方法的检错率均在0.95左右，TCN方法的检错率略高于LSTM方法，SVR方法的检错率相对较差在0.92左右。由此说明，LMD-TCN方法能有效地检测出数据中存在的疑误数据，具有较强的稳定性和误差识别能力。

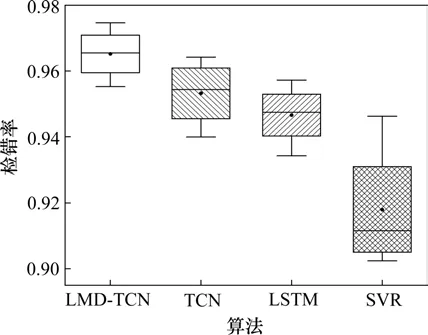
图6 不同算法不同站点的检错率Fig.6 Error detection rate of different algorithms at different sites

分别使用LMD-TCN，TCN，LSTM和SVR方法对南京大胜关长江大桥站2018年不同季节的风速数据进行质量控制，检错效果如图7所示。由图7可知，4种不同算法在南京大胜关长江大桥站不同季节的检错率变化趋势基本一致，秋季和春季的检错率较高，冬季和夏季次之。南京大胜关长江大桥站位于江面且夏季受台风的影响，风速波动变化大，因而检错率比秋季和春季的低；而其冬季的检错率，从图5(d)中可知，随着质控参数f的增大，第1类错误的下降幅度及第2类错误的上升幅度均比秋季和春季的大，检错率也迅速下降。LMD-TCN方法与TCN方法在秋季的检错率相差不大，其原因是南京大胜关大桥站秋季风速波动变化相对较小，2种方法得到的预测值的RMSE均在0.08左右，NSC均在0.998左右，拟合效果好，预测值接近风速的实际变化，检错率之间的差距较小。在不同的季节，LMD-TCN方法在南京大胜关长江大桥站的检错率高于传统的TCN方法，传统的TCN方法和LSTM方法检错率相差不大，且这2种方法的检错效果均优于SVR方法。以上结果表明，在不同的季节，LMD-TCN方法均具有较强的检错能力，季节适应性强。

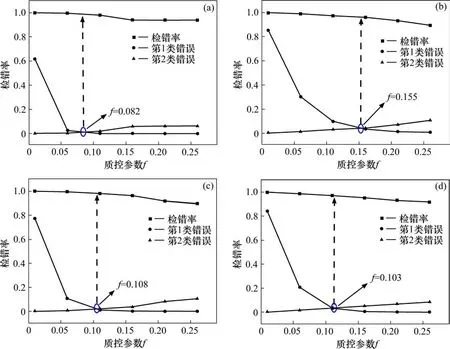
图5 质控参数与2类错误关系Fig.5 Relationship between quality control parameters and two kinds of errors

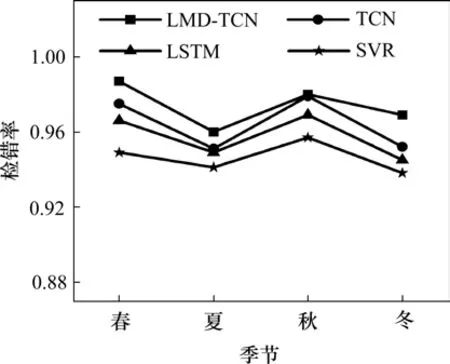
图7 不同算法不同季节的检错率Fig.7 Error detection rate of different algorithms in different seasons

5 结论

1)LMD-TCN质量控制算法适用于风速观测资料的单站质量控制，在京沪高铁沿线江苏段4个观测站不同季节的检错率均达到90%以上，季节适应能力较强且误差检测能力较高。

2)LMD-TCN质量控制算法与TCN算法、LSTM算法及SVR算法相比，在不同地理位置、不同季节下，LMD-TCN算法均能有效地检测出风速观测资料中的可疑数据，具有更好的质量控制效果。

3)最佳质控参数f的选取需视具体情况而定，不同地区不同季节的最佳质控参数不一致，以第1类误差和第2类误差的“最小”原则为选取依据，以提高质量控制算法的检错率。

4)LMD-TCN质量控制算法目前仅涉及单一的风速时间序列，并未考虑其他气象要素如温度、湿度和气压等对风速的影响。后续的研究将把其他气象要素融入LMD-TCN质量控制算法中，以进一步提高算法的泛化能力和质控效果。