非金属元素(F, S, Se, Te)掺杂对ZnO/graphene肖特基界面电荷及肖特基调控的理论研究

2022-05-17庞国旺刘晨曦潘多桥史蕾倩张丽丽雷博程赵旭才黄以能

人工晶体学报 2022年4期

庞国旺，刘晨曦，潘多桥，史蕾倩，张丽丽，雷博程，赵旭才，黄以能,2，汤哲

(1.伊犁师范大学物理科学与技术学院，新疆凝聚态相变与微结构实验室，伊宁 835000；2.南京大学物理学院，固体微结构物理国家重点实验室，南京 210093)

0 引言

随着社会的快速发展，人们对信息的需求量增大，纳米电子、光电子和量子通信的量子力学效应受到越来越多的关注，作为21世纪以来发展最快的半导体器件，其工艺尺寸越来越接近硅工艺的极限，单位面积内集成晶体管数量的提高导致功耗不断增加，晶体管应用需要其他替代材料[1-2]。自2004年石墨烯(graphene)被科研人员成功剥离以来[3]，以graphene为代表的二维材料因其优异的电学、光学、力学、热学性质，引起了科研工作者的广泛关注[4-5]。graphene作为典型的二维材料，具有优异的力学性能[6]、比表面积[7]，有较高的载流子迁移率[8]和热导率[9]，因此被广泛应用于电极修饰、化学电源、传感器等领域。然而，由于graphene特殊的结构特征导致其带隙为零，电子空穴极易复合，严重阻碍了其在电子与光电子器件应用领域的发展。此外，由于graphene的厚度只有一个原子层，在一般的实际应用中，需要找到一种载体才能充分发挥其优异的性能[10]。ZnO是一种具有直接带隙的半导体材料，其激子结合能高、稳定性好、抗辐射能力强，这些优点使ZnO广泛应用于太阳能电池、传感器、光催化剂等领域[11-12]。2006年Freeman等[13]从理论上预言：当ZnO薄膜的厚度接近于几个原子层时，它将从体相的纤锌矿结构向石墨相转变。目前，Tusche等[14]在Ag(111)衬底上生长出了2个单原子层厚度的ZnO(0001)薄膜，证实了Freeman的预测。近年来，利用范德瓦耳斯异质结将两种二维材料结合起来应用于肖特基二极管、场效应晶体管、光电器件和集成电路已成为研究热点[15-16]。研究者通过设计二维异质结层间结构可以构造出性能优异的光电器件。如果将ZnO和graphene有机结合起来，不仅可以为graphene提供载体，还能弥补ZnO自身导电性能方面的不足，因此，开展ZnO/graphene异质结复合材料的研究具有重要的现实意义。目前，人们对ZnO/graphene异质结进行了研究。如Xu等[17]通过第一性原理对ZnO/graphene异质结的电子特性进行了计算，发现ZnO/graphene界面处存在范德瓦耳斯力，ZnO和graphene之间由于功函数不同而发生电荷转移，ZnO和graphene形成异质结后，graphene的狄拉克点仍然存在，这意味着它与ZnO的相互作用不会影响其优异的导电性。Liu等[18]构建了ZnO/graphene肖特基结，发现其对紫外线照明显示出相当高的响应度和快速开关比，并且发现当施加-0.349%的应变时，应变诱导的压电势对肖特基势垒高度的改变，从而促进了ZnO/graphene界面中的电子-空穴分离使得材料的光敏性能提高了17%。

掺杂是半导体器件或集成电路工艺中最重要的一个环节，通过控制杂质类型和浓度，可以控制半导体的光电特性。Li等[19]在实验上对ZnO/graphene异质结进行了B元素掺杂，随着B离子掺杂浓度的增加，薄膜表面的颗粒尺寸减小，肖特基接触表现出良好的整流行为。马浩浩等[20]研究了C、O、N、B掺杂对WS2/graphene肖特基接触的影响，发现N、B掺入后，异质结呈现欧姆接触；C、O掺入后肖特基类型由p型转变为n型。陶鹏程等[21]发现卤族元素的掺杂可以有效地调制金属-MoS2界面间的肖特基势垒高度。其中F和Cl原子的掺杂降低了体系的肖特基势垒高度，Br和I原子的掺杂增大了体系的肖特基势垒高度。以上工作表明，利用掺杂的方式来调控异质结肖特基的接触类型及势垒高度是切实可行的。然而，到目前为止，利用第一性原理研究非金属元素(F，S，Se，Te)掺杂ZnO/graphene肖特基对其界面电荷分布影响及其肖特基调控的研究鲜有报道，另外，ZnO和graphene的结构特殊性使其片层之间可能存在较弱的相互作用，很难通过实验直接进行探测。

为此，本文建立了ZnO/graphene异质结模型，采用基于第一性原理的密度泛函理论研究了ZnO/graphene界面结合作用及其对电子结构的影响，讨论了F、S、Se、Te四种非金属元素对肖特基接触类型和势垒高度的调控，以期找出能够降低肖特基势垒的具体掺杂元素及方式，为设计和制造相关的场效应晶体管提供一定的参考。

1 模型和计算方法

本文所有的计算均基于密度泛函理论(DFT)的平面波超软赝势方法(USP)，利用Materials Studio 2017软件中的CASTEP[22]模块完成。采用GGA-PBE[23]方法分别对单层graphene晶胞和单层ZnO晶胞进行几何优化，优化时采用BFGS算法完成。其中graphene优化后的晶格常数a=b=0.246 nm，与已报道的实验值[24]误差小于1%，ZnO晶胞优化后的晶格常数a=b=0.328 nm，接近Gao等[25]的计算结果。根据优化后的晶格常数选取单层ZnO的周期性结构为3×3×1，为了避免掺杂直接破坏graphene狄拉克锥，本文主要考虑在ZnO层进行掺杂。为了避免边界效应，本文选取坐标为(0.444，0.555，0.026)的一个O原子分别被F、S、Se、Te替换，如图1所示，在替换的基础上与4×4×1的graphene搭建异质结，为了说明ZnO/graphene异质结层间的相互作用及其稳定性，本文利用Eb=E(ZnO/graphene)-E(ZnO)-E(graphene)计算了不同层间距下的结合能，如图2所示。其中E(ZnO/graphene)，E(ZnO)和E(graphene)分别对应优化后ZnO/graphene异质结、单层ZnO和graphene的总能量。结果显示当异质结的层间距为0.35 nm时结合能最低，为-3.86 eV，表明ZnO/graphene异质结最稳定的层间距为0.35 nm，远大于C原子与O原子、C原子与Zn原子之和，与graphene/MoSe2[26]和graphene/ZnO[17]等graphene基异质结的数据接近。这说明在ZnO/graphene异质结层间存在范德瓦耳斯相互作用。为了准确描述异质结层间的范德瓦耳斯力，本文选取了GGA-PBE方案中的Tkatchenko-Scheffler(TS)[27]色散修正。布里渊区网格采用以Gamma点为中心的Monkhorst-Pack[28]方案，选取5×5×2的K点网格，每个原子的位移不超过1×10-4nm，每个原子所承受的应力不超过0.1 GPa，平面波动截断能设置为520 eV，自洽收敛精度为2.0×10-5eV/atom，原子间受力不超过0.5 eV/nm。z轴方向真空层厚度设置为1.8 nm。

图1 单层ZnO 3×3×1超胞掺杂俯视图:(a)Zn9O8F1俯视图；(b)Zn9O8S1俯视图；(c)Zn9O8Se1俯视图；(d)Zn9O8Te1俯视图Fig.1 Top view of monolayer ZnO 3×3×1 supercell doping: (a) Zn9O8F1 top view; (b) Zn9O8S1 top view; (c) Zn9O8Se1 top view; (d) Zn9O8Te1 top view

图2 ZnO/graphene异质结基态能量与层间距的关系Fig.2 Relationship between binding energy and interlayer distance of ZnO/graphene heterojunction

2 结果与讨论

2.1 结构稳定性分析

为了研究五种异质结的匹配程度，计算了Zn9O8X1/graphene(X=O，F，S，Se，Te)异质结的晶格失配率，公式为δ=(a2-a1)/a1，其中a1为单层Zn9O8X1(X=O，F，S，Se，Te)超胞晶格常数，a2为graphene超胞晶格常数，计算结果如表1所示，分析发现掺杂后异质结体系的失配率均小于ZnO/graphene异质结，掺杂前后的五种体系的晶格失配率均低于5%，满足完全共格条件。

表1 Zn9O8X1/graphene(X=O，F，S，Se，Te)晶胞参数Table 1 Cell parameters of Zn9O8X1/graphene (X=O, F, S, Se, Te)

在两种二维材料形成稳定界面的过程中，由于晶格不匹配会导致失配能的产生，并且晶格失配能越小表明异质结体系越稳定。为了进一步探究异质结结构的稳定性，本文计算了各体系的晶格失配能[29]。

ΔEmismatch=[E(graphene)a′+E(Zn9O8X1)a′-E(graphene)a-E(Zn9O8X1)a]/S

(1)

式中：E(graphene)a′为优化后单层graphene的能量；E(Zn9O8X1)a′为优化后单层Zn9O8X1(X=O，F，S，Se，Te)的能量；E(graphene)a为优化前单层graphene的能量；E(Zn9O8X1)a为优化前单层Zn9O8X1(X=O，F，S，Se，Te)的能量；S为异质结的表面积。从表1看出，掺入F原子时，体系的晶格失配能最高，说明掺入F原子后，相比于未掺杂体系稳定性有所降低；当分别掺入S、Se、Te原子时，各体系的晶格失配能均低于ZnO/graphene异质结，表明掺杂提高了ZnO/graphene异质结的稳定性。另外，表1中各体系的范德瓦耳斯作用力的能量值分布在1.125 eV/nm2至13.992 eV/nm2之间，与之前的报道的数值[30]非常接近，说明本文所构建的5种异质结体系层间的作用力为范德瓦耳斯力。

2.2 能带结构

能带结构图可以很好地反映异质结层间相互作用对电子的影响，在计算ZnO/graphene异质结能带时，为了与ZnO/graphene异质结能带图进行对比分析，首先计算了如图3所示的单层ZnO(a)和单层graphene(b)。由图3(a)可以看出，单层ZnO的导带底和价带顶均位于高对称点G，为直接带隙，带隙宽度为1.67 eV，接近文献[31]的计算结果。从图3(b)可以看出，graphene具有特殊的能带色散关系，在倒易空间的K点处形成了导带和价带相交的狄拉克锥(Dirac cone)[32]导致带隙为零，这表明graphene是一种无带隙的半导体，并具有金属性质，与文献[33]的结果保持一致，说明本文所建立的模型和计算结果是合理的。图3(c)是ZnO/graphene异质结能带图，通过与单层的ZnO和graphene的能带进行对比发现，层间杂化和电荷转移对异质结能带结构的影响不大，异质结的能带几乎是由单层graphene和单层ZnO能带结构的简单叠加，说明ZnO和graphene之间的作用非常弱，对各自电子态的影响非常小，与上文的稳定性分析相一致。ZnO/graphene异质结中，graphene电子态狄拉克锥仍然存在，ZnO的导带底和价带顶均向下移动，这是因为单层graphene和单层ZnO之间存在电势差，当两者接触形成肖特基时，界面电荷将会从电势较高的graphene向电势较低的ZnO转移。另外，根据肖特基-莫特模型[34]可知：导带底与费米能级之间的能量差为n型肖特基势垒高度(n type Schottky barrier height， n-SBH)；价带顶与费米能级之间的能量差为p型肖特基势垒高度(p type Schottky barrier height， p-SBH)。在图3(c)发现导带底相对于价带顶更接近费米能级，n-SBH=0.83 eV，表明graphene和ZnO接触呈现n型肖特基接触。以上结果表明，当ZnO/graphene异质结作为电极材料时，不仅发挥了graphene优越的导电性能而且还保持了本征ZnO的特性。

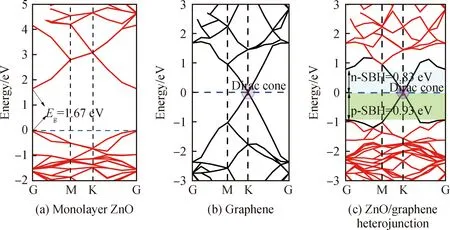
图3 能带结构图Fig.3 Band structure diagram

图4(a)～(c)分别为单层graphene、单层ZnO和ZnO/graphene异质结的功函数，功函数表示电子从材料表面逃逸到自由空间中所需的最小能量。从图4中可以看出，ZnO/graphene异质结的功函数为4.192 eV，小于单层ZnO的功函数(4.735 eV)，但大于graphene的功函数(4.046 eV)。功函数的不同将会导致层间电荷发生转移，本文中当graphene与ZnO形成异质结时，graphene中的部分负电荷向ZnO层转移。为了更清晰地描述层间电荷的转移情况，本文计算了异质结的差分电荷密度，如图5所示。

图4 功函数图Fig.4 Work function diagram

差分电荷密度图可以呈现异质结层间电荷的转移情况，图5中青色区域代表负电荷的耗散(正电荷聚集区域)，黄色区域代表负电荷的积累(负电荷聚集区域)。当graphene与ZnO形成异质结时，graphene中的部分负电荷向ZnO层转移，导致ZnO层聚集了大量负电荷，ZnO的能级向低能态移动，与能带图分析相一致。另外，由于电荷的转移导致graphene层空穴浓度增加，ZnO层电子浓度增加，形成了由graphene到ZnO方向的内建电场，在界面处产生了电子势垒，阻止了电子从graphene到单层ZnO的扩散，使得电子的扩散和漂移运动达到平衡。

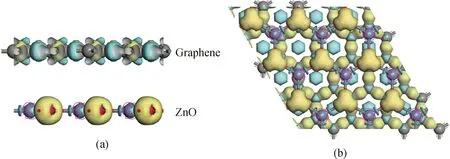
图5 ZnO/graphene异质结的三维电子密度差分图:(a)侧视图;(b)俯视图。青色区域代表负电荷的耗散，黄色区域代表负电荷的积累Fig.5 Three-dimensional electron density difference diagram of ZnO/graphene heterojunction: (a) side view; (b) top view. Blue area represents dissipation of negative charge, yellow area represents accumulation of negative charge

2.3 肖特基调控

异质结的肖特基调控主要是指对肖特基接触类型和肖特基势垒高度的调控。大量的实验和理论表明，通过对异质结施加电场、应力、掺杂、空位、吸附等可以实现对异质结肖特基接触类型和肖特基势垒高度的调控。因此本文通过掺杂的方式影响ZnO/graphene异质结层间电荷的转移进而调控异质结的肖特基接触类型和势垒高度的方法是完全可行的。本文选取F、S、Se、Te分别替换了ZnO中的1个O原子。为了更清楚地描述非金属掺杂对ZnO/graphene异质结的影响，首先分析了非金属元素对单层ZnO能带结构的影响，如图6所示。

图6 能带图:(a)Zn9O8F1；(b)Zn9O8S1；(c)Zn9O8Se1；(d)Zn9O8Te1Fig.6 Band diagram: (a) Zn9O8F1; (b) Zn9O8S1; (c) Zn9O8Se1; (d) Zn9O8Te1

从图6(a)可以看出，当F原子掺入ZnO后，体系的能级均向下发生移动，导带下移2.23 eV，价带下移2.15 eV，带隙由1.67 eV变为1.59 eV，另外，导带底穿过费米能级，体系呈现n型半导体特征。从图6(b)～(d)可以看出，当掺入S、Se、Te时，体系能带的价带顶均位于费米能级处，与图6(a)本征ZnO相比并无明显的变化，而体系的导带底随着不同元素的掺入，相应地发生了不同程度的移动，其中掺入S和Se元素时，体系的导带底分别上移0.32 eV和0.18 eV，导致其带隙分别为1.99 eV和1.85 eV。掺入Te元素后，体系的导带底下移0.38 eV，其带隙也相应地变为1.29 eV。可以发现，F、S、Se、Te四种非金属元素掺入ZnO后，对体系的带隙产生了明显的影响。为了更深入地探究F、S、Se、Te四种非金属元素对ZnO/graphene异质结肖特基接触类型和势垒的影响，计算了掺杂后异质结体系的能带，如图7所示。

结合图7及表2可以观察到，图7(a)中当F元素掺入ZnO/graphene异质结体系后，graphene的狄拉克点位于费米能级的下方，价带中存在未填充能级。此外，F原子的掺入引起了能级的大幅度下移，这是因为F原子的外围电子数多于O原子的外围电子数，当F原子替换O原子后，将会向ZnO中注入电子，引起能级向下移动，并且导带底穿过费米能级，导致异质结呈现欧姆接触；从图7(b)～(d)可以发现，当ZnS、ZnSe和ZnTe分别与graphene接触时，gaphene的狄拉克点均停留在费米面上。另外，相对于单层Zn9O8X1(X=S、Se、Te)的能级而言，Zn9O8X1/graphene(X=S、Se、Te)异质结体系中Zn9O8X1(X=S、Se、Te)的价带顶分别下移0.83 eV、0.73 eV和0.48 eV，主要是由于当graphene与Zn9O8X1(X=S、Se、Te)形成异质结时，graphene中的部分负电荷向Zn9O8X1(X=S、Se、Te)层转移，导致Zn9O8X1(X=S、Se、Te)层聚集了大量负电荷，电势降低，能级向低能态发生移动。此时，Zn9O8X1/graphene(X=S、Se、Te)三种异质结中的n型肖特基势垒分别为0.97 eV、0.99 eV和1.05 eV，p型肖特基势垒分别为0.83 eV、0.73 eV和0.48 eV，三种异质结类型均为p型肖特基接触。说明掺入S、Se和Te原子不仅可以实现异质结肖特基接触类型由n型向p型的转变而且还能有效地降低肖特基势垒的高度。

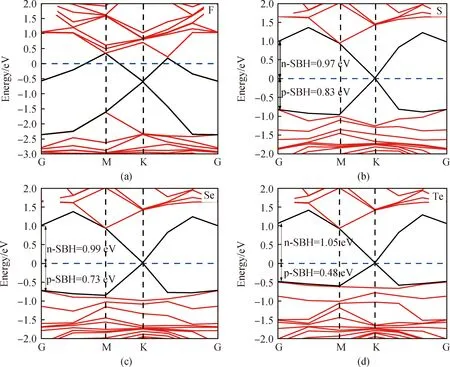
图7 能带图:(a)Zn9O8F1/graphene；(b)Zn9O8S1/graphene；(c)Zn9O8Se1/graphene；(d)Zn9O8Te1/graphene。图中黑色的能带由graphene贡献Fig.7 Band diagram: (a) Zn9O8F1/graphene; (b) Zn9O8S1/graphene; (c) Zn9O8Se1/graphene; (d) Zn9O8Te1/graphene. The black energy band is contributed by graphene