含隧道缺陷铝合金FSW 搭接接头疲劳寿命预测
2022-05-14杨庆鹤王瑞杰赵红阳武陇岗覃秋雷
杨庆鹤,王瑞杰*,,赵红阳,武陇岗,覃秋雷
(1.昆明理工大学 机电工程学院,昆明 650500;2.辽宁科技大学 材料与冶金学院,辽宁鞍山 114001)
搅拌摩擦焊(Friction stir welding,FSW)作为固态焊接工艺,自发明至今被广泛应用在轨道客车、船舶、航天等领域[1-2]。FSW 虽然在焊接轻质金属时可以显著提高焊接质量,但工艺参数对焊接质量影响很大,当工艺参数不合适时即产生缺陷,如隧道缺陷[3]。隧道缺陷是较为常见的由工艺参数不合适引起的缺陷,根本原因是焊接热量不足导致焊缝区域塑性状态金属填充不足,形成隧道缺陷,搅拌针形状对隧道缺陷的形状有影响,隧道缺陷会降低试件的抗拉强度和弯曲力学性能[4-5]。另外,许多研究表明,FSW 搭接试件都会在焊缝前进侧和后退侧出现类似未连接的钩状区域,即钩状缺陷[6-7]。钩状缺陷是降低接头疲劳强度的关键因素,提高焊接工艺及改善搅拌头都可以降低钩状缺陷影响[8-9]。
FSW 接头受材料及加工工艺影响较大,目前对其强度评估及寿命预测没有统一标准。FSW 接头由于其固有钩状缺陷更易造成应力集中,对其疲劳寿命影响较大。Wang 等[10]分别采用局部应力法和结构应力法对镁铝合金FSW 搭接接头进行了疲劳寿命预测,认为结构应力法可以合理给出应力与寿命的关系,局部应力法在低周疲劳下可以给出较为准确的结果,在高周疲劳下预测结果较为分散。牛亚辉等[11]采用裂纹模拟法和临界距离法对FSW 接头进行了寿命预测,认为裂纹模拟法可以给出合理的疲劳评估,该方法不具网格敏感性,临界距离法的预测结果较准确,该方法具有网格敏感性。王小娇等[12]利用红外热像技术对镁合金FSW 接头的疲劳裂纹扩展行为进行了研究,发现应力强度因子、裂纹扩展速率和材料表面温度演变存在一一对应关系,还发现裂纹扩展速率与应力强度因子呈线性关系。实际应用中铝合金焊接件需要评估疲劳性能,以便能更精确的预测铝合金FSW 接头的疲劳寿命,防止重大安全事故的发生。
本文拟对FSW 搭接接头钩状缺陷及隧道缺陷区域进行显微观察,对试件进行疲劳加载,观察断裂处特征,进而通过有限元方法分析FSW 搭接接头焊缝附近的应力变化,对试件的疲劳寿命进行预测,并与试验结果进行对比。
1 试验方法
试验采用6061-T6 铝合金板制备的FSW 搭接接头,其母材化学成分和力学性能见表1 及表2[13]。
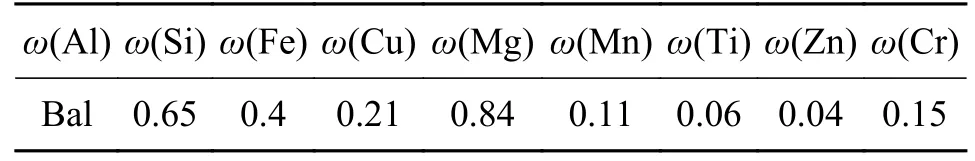
表1 6 061-T6 铝合金化学成分 %

表2 6 061-T6 铝合金力学性能
试件是由两块厚度为3 mm 的6061-T6 铝合金板通过FSW 工艺焊接而成,在辽宁科技大学完成焊接。将已经焊接完成的板材分割成若干宽为8 mm、长为208 mm 的试件,如图1 所示。并将试件表面打磨光滑以减小表面缺陷对实验的影响。采用MTS809 材料疲劳试验机对试件进行疲劳加载,试验用载荷波形为ramp 波,实验均在室温条件下进行,加载方向垂直于焊缝,加载频率均为10 Hz。本次设计了两种恒幅加载方案,方案一中的载荷比恒定为0.1,方案二为变化载荷比,具体方案如表3 及表4 所示,随机选取打磨好的试件进行编号、测试。
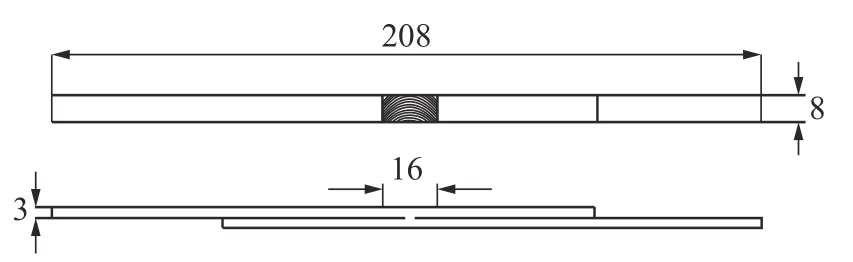
图1 试件几何尺寸

表3 加载方案一
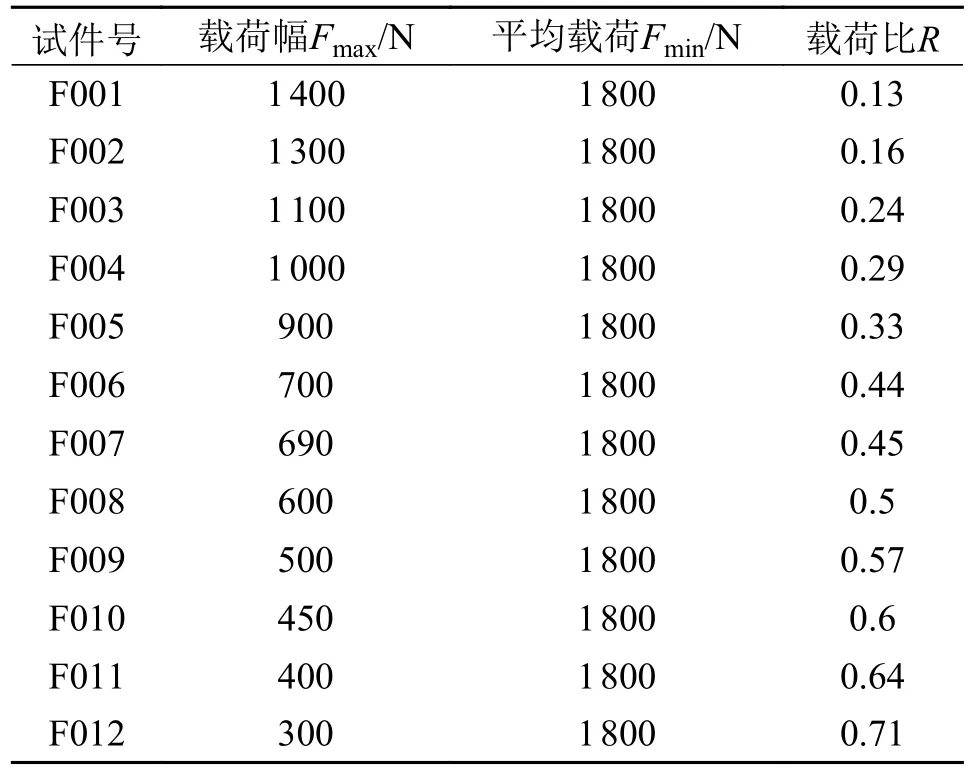
表4 加载方案二
2 疲劳试验结果分析
试件接头如图2a)所示。从图2a)和图2b)可以看出,不同试件上存在形状和大小都有所区别的隧道缺陷,位置都接近后退侧。从图2a)可以看出,后退侧的钩状缺陷趋近直线,前进侧钩状缺陷发生翘起。试件在拉伸过程中,板材发生弯曲,如图2b)所示,但依然可以看出裂纹基本沿板厚方向扩展直至断裂;从图2c)可以看到试件从焊接接头后退侧的钩状缺陷根部断裂,故可认为钩状缺陷是接头断裂的主要因素。

图2 试件接头
在双对数坐标系下,以试验疲劳寿命N为横坐标,以疲劳载荷名义应力幅S为纵坐标,采用最小二乘法对试验数据作线性回归拟合,结果如图3 所示,名义应力为载荷幅除以板横截面积。

图3 试验结果 S-N 曲线
从图3 中可以看出不同的应力比对本次实验寿命影响不明显。尽管试件的隧道缺陷尺寸各不相同,但S-N曲线仍呈明显的线性关系,图3 为应力幅与疲劳寿命之间的关系,方案一和方案二的线性拟合结果分别为:

3 应力应变有限元分析及寿命预测
3.1 缺口应力法预测疲劳寿命
3.1.1 有限元建模与加载
本次试验所用的FSW 搭接接头除有钩状缺陷这种固有缺陷,还含隧道缺陷。首先使用工业显微镜对完好试件接头侧面进行整体拍照,隧道缺陷尺寸、形状各异,孔洞基本都位于靠近后退侧的焊核区域,典型的隧道缺陷如图2a)所示。
由于FSW 焊接是固相连接技术,焊核残余应力较小[14],本文假定各区域材料性能与母材是一致的。利用ABAQUS 有限元软件对试件进行应力分析。应用缺口应力法分析只需进行弹性建模,有学者提出在弹性建模时将隧道缺陷可近似建为圆形孔洞[15]。根据实际孔洞的尺寸建立相应的模型,本模型中孔洞的直径大小在0.4~ 1.1 mm 之间,模型中孔洞直径为真实隧道缺陷最大尺寸。以孔洞尺寸为0.92 mm 的试件为例,为减少计算量,全部采用二维应变单元CPE4,该试件模型有27 456 个节点,26 504个CPE4 单元。网格的疏密由应力集中程度决定,在应力集中较大处适当加大网格密度,如图4 所示。
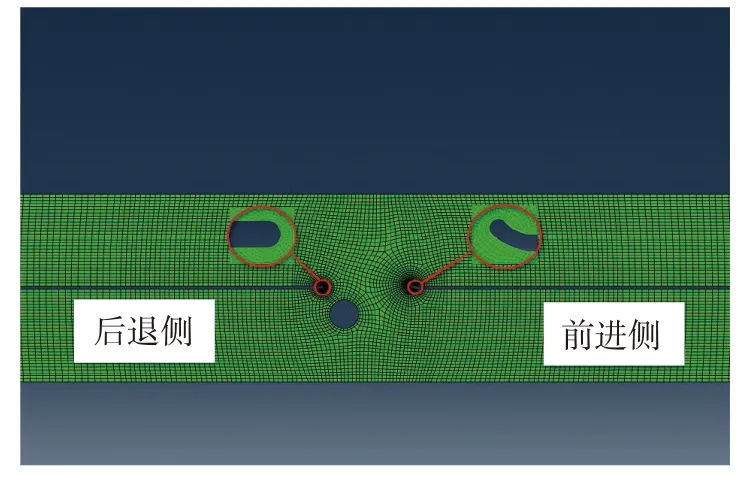
图4 虚拟缺口有限元模型
缺口应力法是从弹性的角度出发求解缺口应力场和确定缺口应力应变寿命分析方法[16]。建模时将钩状缺陷简化为有一定半径的虚拟缺口,前进侧钩状缺陷有一定角度的翘起,如图2a)所示,后退侧趋近一条直线,本次建立模型如图4 所示。依据IIW推荐标准[17],虚拟缺口半径为0.05 mm。
按照试件真实的孔洞大小及钩状缺陷角度建立相应的模型,考虑在实验过程中疲劳试验机夹持力的影响,对试件夹持部分施加位移约束,将模型左端设置为全约束,右端施加拉载荷,右端除施加载荷方向的自由度外,其余自由度全部约束。实验中使用ramp 波进行加载,故在ABAQUS 有限元模拟过程中设置3 个载荷步,第一步和第三步所加载荷为最大载荷,第二步施加最小载荷,约束及加载如图5 所示。进行弹性应力分析,根据IIW 标准,使用应力集中程度最大处的最大主应力进行寿命预测。6061-T6 铝合金弹性模量为65.9 GPa,泊松比为0.33[18]。

图5 有限元模型约束与加载
3.1.2 疲劳寿命预测
IIW 定义了焊接接头的疲劳等级曲线[19],用循环次数Nf=2×106处的应力范围值Δσf作为疲劳等级值FAT,该曲线的拐点设定在107,拐点之后考虑了小载荷的影响,采用了m2的斜线段。曲线分为上下两端,S-N曲线方程为:
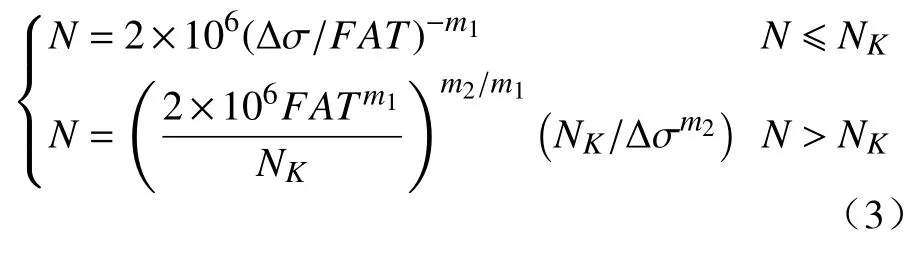
式中:N为循环次数;NK为拐点处循环次数;FAT为疲劳等级;m1为曲线上半段斜率;m2为曲线下半段斜率。
依据IIW 标准,铝合金FSW 搭接接头在应力疲劳等级FAT为180,本次试验寿命均在2×106以下,即取上半段斜率m1=3,铝合金曲线见图6。
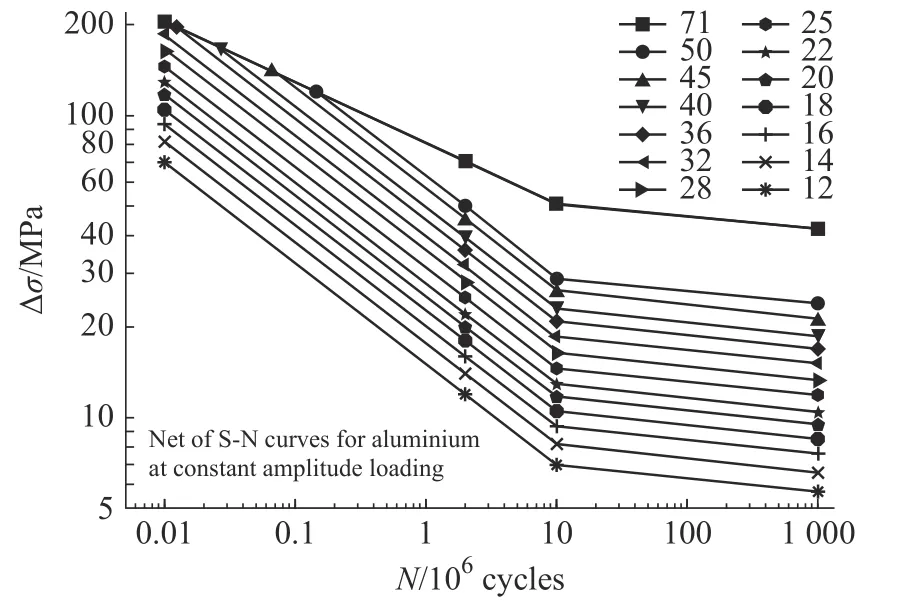
图6 铝合金疲劳曲线
图7 为接头钩状处的最大主应力云图,从图7中可以看出该模型的后侧钩状缺陷较前侧钩状缺陷应力集中程度大。将钩状缺陷处应力集中程度最大单元的主应力幅代入式(3)计算出疲劳寿命,两种方案预测寿命与实验寿命的对比如图8 所示。从图8可以看出预测寿命与实验寿命误差在两个因子以内,在105以内线性关系较为明显,预测值基本大于试验值。当预测值超过105时,预测值有远离线性关系的趋势,变得有些保守,但误差基本在两个因子以内。
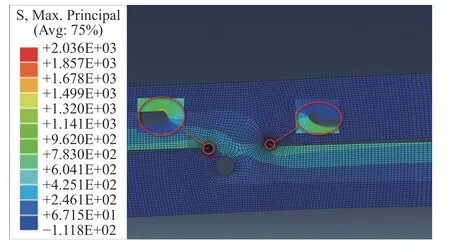
图7 有限元最大主应力云图

图8 缺口应力法预测寿命
3.2 线弹性断裂力学法预测疲劳寿命
3.2.1 建立线弹性断裂力学模型
本次试验接头中钩状缺陷根部较为尖锐,钩状缺陷处的应力集中严重,无法直接按照实际形状建模直接求得准确的应力,应用Paris公式计算裂纹扩展寿命进而估算接头疲劳寿命。由于搭接接头存在钩状缺陷,在拉伸时裂纹附件的节点同时存在竖直和水平方向的应力与位移,属于复合型开裂问题,存在I 型裂纹和II 型裂纹。
试件疲劳寿命由裂纹萌生寿命和裂纹扩展寿命组成,通常认为裂纹在a0之前为裂纹萌生阶段,也有学者认为这阶段属于短裂纹阶段,但同时也指出该阶段不适用线弹性裂纹扩展规律[20]。本文不考虑短裂纹这种情况。裂纹长度达到a0之后,进入裂纹扩展阶段,此阶段符合线弹性扩展规律。在本次实验中试件都在后退侧断裂,故重点考虑后退侧应力集中问题,从图2b)可以看出裂纹基本沿着板厚方向,故建立模型如图9a)所示,在后退侧按照实际尺寸建立模型,并在钩状缺陷根部建立长度为a0的初始裂纹,初始裂纹方向沿着板厚方向,在前进侧采用虚拟缺口法对钩状缺陷进行处理,虚拟缺口半径为0.05 mm,隧道缺陷近似简化为圆孔处理。为减少运算量,建立二维有限元模型,以孔洞尺寸为0.92 mm的试件为例,该模型共有10 651 个节点,9 957 个CPE4 单元,12 个CPE3 单元。根据隧道缺陷的位置、尺寸建立不同的有限元模型,在应力较集中的区域适当增大网格密度,初始裂纹附近网格划分如图9b)所示。
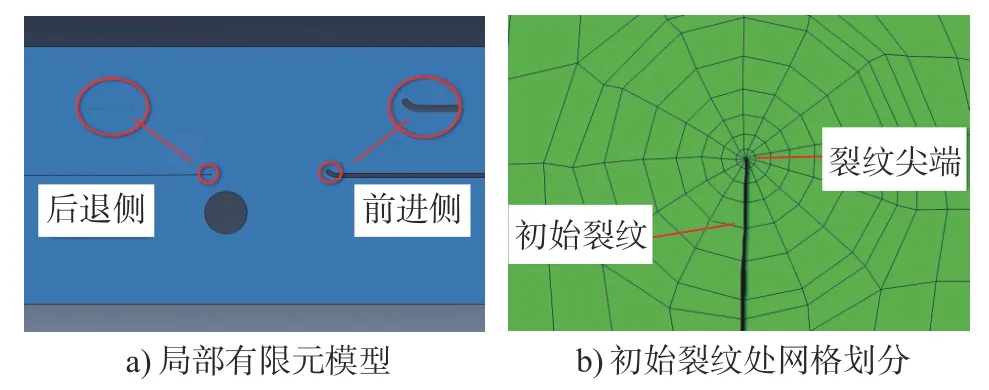
图9 有限元模型局部
每个试件隧道缺陷尺寸、位置各异,对每个试件建立相应的模型,并施加相应的实验载荷,在ABAQUS 软件进行Contour integral 裂纹有限元分析,可以得到Ⅰ型应力强度因子K和Ⅱ型应力强度因子K,进而求得等效应力因子Ke,并用其进行强度评估。约束条件及施加载荷与上述缺口法加载相同。
3.2.2 利用裂纹扩展寿命预测总疲劳寿命
目前在断裂力学中,Paris公式是最为重要的疲劳裂纹扩展模型。式中,ΔK为应力强度因子幅度值、材料参数C和m、初始裂纹长度a0以及扩展速率da/dN是主要控制因素,其关系式为
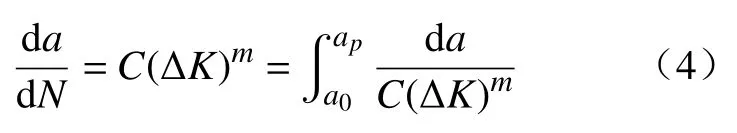
材料参数C和m可由IIW 查得,对于铝合金分别为1.41×10-11和3。将疲劳断口置于NOVA Nano SEM 450 电子显微镜下进行观测,如图10 所示。对于临界裂纹长度,可通过测量疲劳断口图获得,从图10a)可以发现瞬断区与扩展区有明显界限,扩展区表面较为光滑,瞬断区较粗糙。图10b)和图10c)为不同载荷下疲劳断口图,可以明显发现低周疲劳的瞬断区长度较高周疲劳长,通过测量试件断口发现瞬断区长度约占板厚的20%~40%,所以临界裂纹长度约为板厚的60%~80%,不同试件按实际测量长度为准。

图10 疲劳断口图
由于初始裂纹难以测量,裂纹萌生尺寸和裂纹扩展尺寸之间没有统一标准区分,Bhattacharya 对多种材料研究后提出“工业裂纹尺寸”概念,以0.076 mm作为裂纹萌生阶段的临界长度[21],裂纹超过0.076 mm视为裂纹扩展阶段,本文将该值作为裂纹初始长度。裂纹萌生寿命不能忽略,有学者认为裂纹萌生寿命占总寿命的80%以上[22],在本文中取裂纹萌生寿命占总疲劳寿命的80%,即总寿命Nt=5N。
关于混合型裂纹的断裂准则还没有统一规定,在工程中从安全角度出发,同时考虑最小应变能密度因子理论,得出等效应力因子表达式[23]为
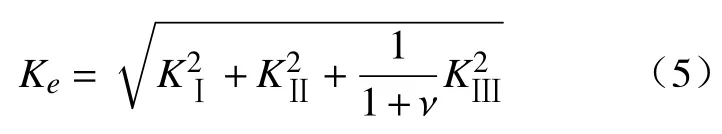
式中:ν为泊松比;在本次试验中Ⅲ型应力强度因子KⅢ=0。
图11 为模型最大主应力云图,可以看出应力集中较大区域在前进侧。在循环载荷作用下,对于最大应力σmax和最小应力σmin,其差值应力幅 Δσ不变,裂纹尖端应力强度因子有相应的最大值Kemax和最小值Kemin,它们之间关系为

图11 有限元最大主应力云图
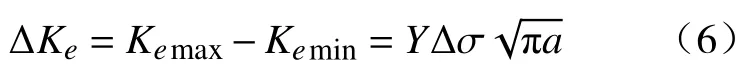
式(6)中Y为几何修正因子,本文试件为边缘穿透裂纹薄板,其Y大小为1.12[24]。
将上述参数及有限元结果数据代入式(4)中计算疲劳寿命,预测寿命与实验寿命的对比如下图12 所示。由图12 可以看出用断裂力学法求出的预测寿命比较保守,基本在2 个因子以内,随着疲劳次数增加,预测结果越来越保守。
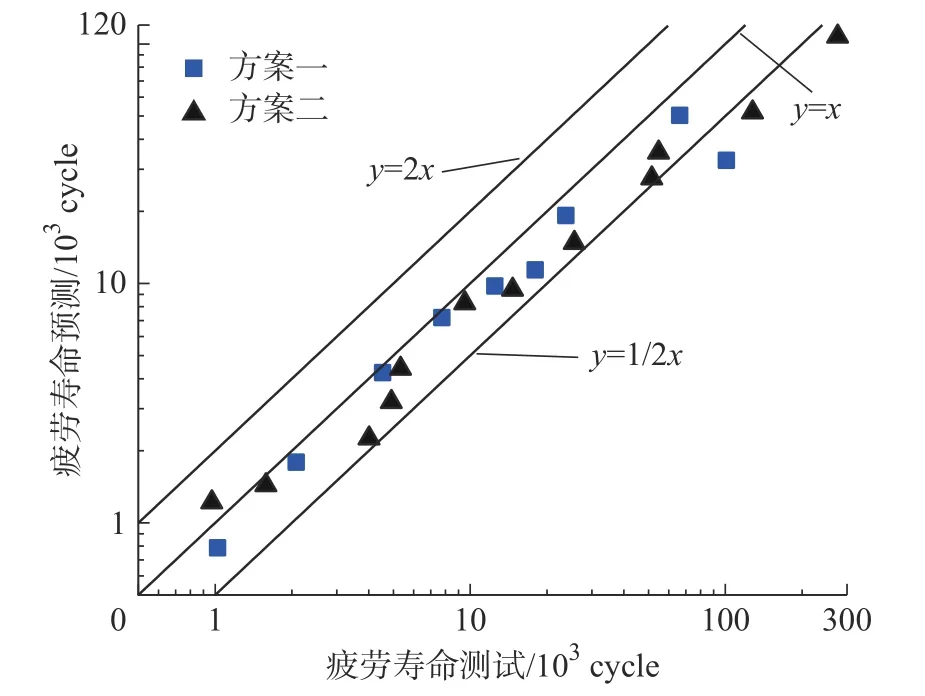
图12 线弹性断裂力学法预测寿命
3.3 预测结果讨论
缺口应力法注重于疲劳薄弱区域的应力变化,在低周疲劳预测中准确性较好,有限元模拟结果显示最大应力集中程度在前进侧钩状缺陷处,与实验结果一致。本次有限元模型的虚拟缺口半径采用IIW 标准推荐值,预测寿命与实验寿命在两个因子以内。从图9 可以看出缺口应力法从低周疲劳到高周疲劳过程中,预测结果越来越保守。
裂纹扩展寿命主要通过计算从初始裂纹扩展到临界裂纹的次数,试件疲劳寿命包含裂纹扩展寿命与裂纹萌生寿命。本文对初始裂纹长度和等效应力强度因子采用工程方法求解,可能是造成预测结果较为保守的原因。
4 隧道缺陷对疲劳寿命的影响
为探索隧道缺陷对疲劳寿命的影响,分别建立无隧道缺陷模型,并对其进行有限元分析,并采用上述两种方法预测其疲劳寿命,其受力如图13 所示。
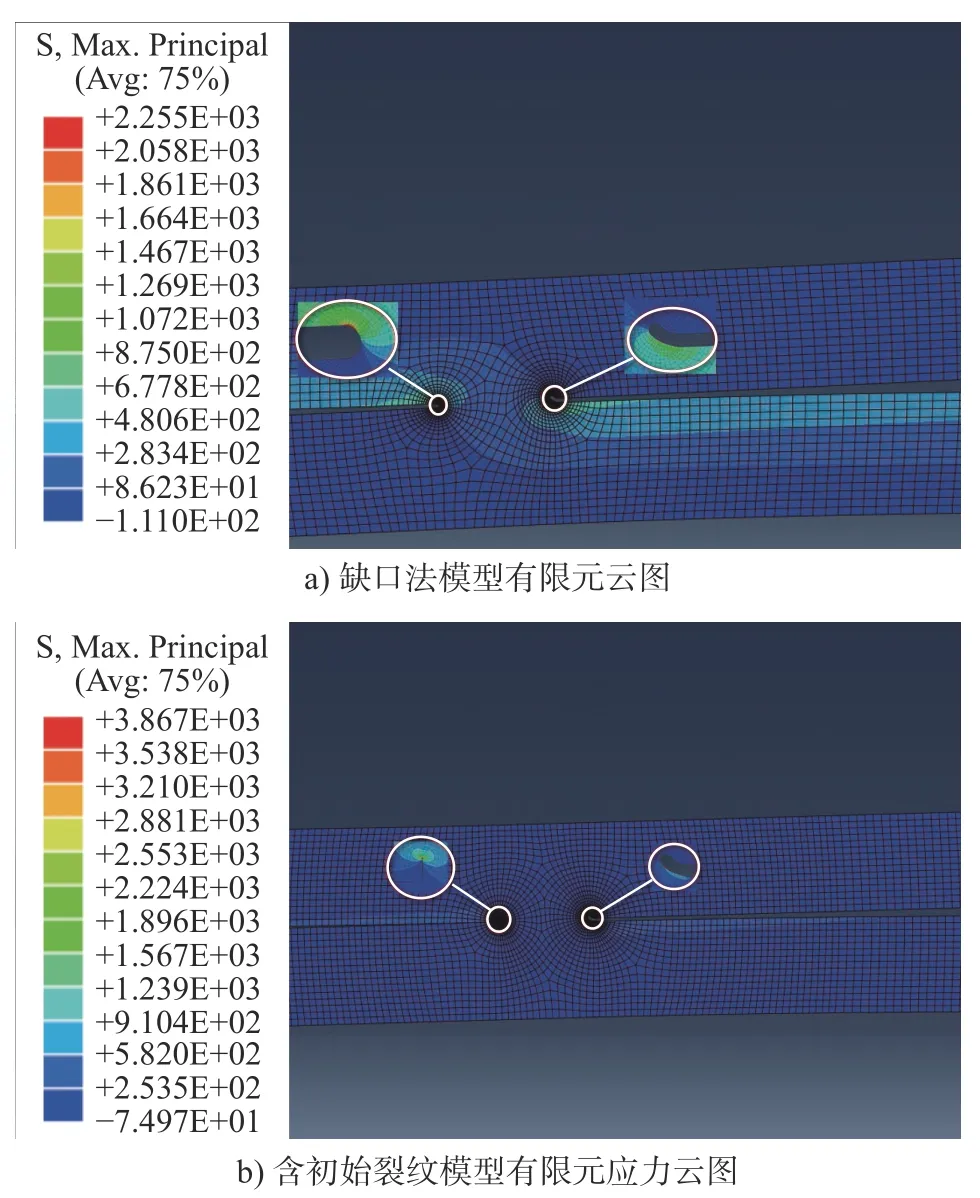
图13 无隧道缺陷模型有限元应力云图
通过两种无隧道缺陷模型可以看出应力较为集中的部位依然在后侧钩状缺陷根部,对比带有缺陷的模型应力云图,发现应力集中区域没有随着隧道缺陷变化而发生转移。
如图14 所示,用两种方法对无隧道缺陷的FSW 搭接接头模型进行寿命预测,对比含隧道缺陷的FSW 搭接接头预测寿命,可以看出隧道缺陷对疲劳寿命影响较小。
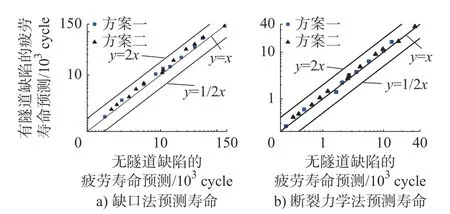
图14 隧道缺陷对寿命影响
5 结论
1)在本次试验中,疲劳断裂位置基本都在后退侧的钩状缺陷处,对比S-N 曲线发现隧道缺陷尺寸对本次试验寿命几乎没有影响;通过无隧道缺陷模型分析也发现隧道缺陷对疲劳寿命影响较小,钩状缺陷对疲劳强度的影响大于隧道缺陷的影响。
2)用缺口应力法和线弹性断裂力学法对FSW 搭接接头进行了寿命预测,缺口应力法预测结果误差在两个因子以内;利用裂纹扩展寿命计算总体疲劳寿命结果较为保守。从预测值和实验值来看,应力比对疲劳寿命影响较小。
(3)本文中在FSW 搭接接头中,将钩状缺陷看成缺口在疲劳寿命预测中取得较好结果。
