多切断点分离-重构技术推导非球型手腕6R 机器人逆解公式

肖帆，曾克俭

（1.湖南工业大学 机械工程学院，湖南株洲 412007；2.湖南工业大学 科技学院，湖南株洲 412007）

机器人逆运动学求解作为机器人离线编程、轨迹规划、控制算法设计等其他课题研究的基础[1]，一直是机器人学中的一个经典问题，同样也是研究热点。逆运动学求解的实质是完成机器人工作空间到关节空间的映射，逆运动学方程组具有高维、非线性的特点，求解复杂且不易求出。

当机器人的结构满足PIEPER[2]准则，即最后3 个关节为轴线交于一点的球型腕部设计时，可以得到解析解。然而该结构的手腕无法实现360°翻转，难以满足在受限空间作业的要求，同时腕部承受能力不强。因而在焊接、喷涂和材料处理等工业中，工业机器人被设计为非球型手腕结构，以使其具有更高的负载能力，更远的水平抵达距离和灵活性[3]，但这也导致该类机器人难以得到逆运动学解析解，并使得机器人的逆运动学非线性方程组变得更复杂，耦合度更高。此时可以利用一般6R 机器人的位姿逆解方法求腕部偏置型6R 机器人的逆运动学解，这些方法主要利用关节的半角正切，将运动学方程转化为1 元16 次多项式进行求解，但是这些方法的公式推导过程十分繁琐耗时[4～6]。

近些年随着计算技术的发展，遗传算法[7]、神经网络算法[8～11]等基于元启发的搜索算法被用于6R 机器人的反解中，但是这类算法仍难以满足实时性控制的要求。肖帆等[12]提出的M-CMA-ES 算法可以满足机械臂的实时求解，但是难以有效地得到非冗余机器人的逆运动学多解，而多解对于机器人避障具有十分重要的意义。李光等[13]提出基于唯一域的方法求非冗余机器人逆运动学多解，该方法需要利用机器人的雅可比矩阵行列式等于零时得到的多项式划分关节空间，而对于许多非球腕结构的机械臂而言，它们的雅可比矩阵行列式通常难以得到简化的相乘的多项式。

刘志忠等[14]、韩磊等[15]均采用球型手腕的逆解作为初始值的数值迭代方法求得了偏置型手腕的逆解，但是该方法难以得到完备的逆解。Wu 等[16]通过两次矩阵逆乘变换，得到了只含θ6的非线性封闭方程，并将该方程的求解转换为最小化问题，由于初始迭代点为随机生成，无法保证算法稳定的计算效率。Trinh 等[17]提出一种几何分析的方法，用于求两款腕部偏置型机器人的逆运动学解，该方法可以得到一个只含未知数θ6的非线性封闭方程。Pashkevich等[18]提出将含6 个未知变量的高斯方程组，转换为用θ6或θ4表示其余5 个关节变量的非线性封闭方程，然后用腕部无偏置型6R 机器人的逆解作为初始值，进行一维迭代求解。Kucuk 等[19]研究了含移动副和转动副的腕部偏置型6R 机器人，利用θ1表示其余5 个关节变量，采用与文献[15]类似的方法求得逆解。Husty 等[20]提出将6R 串联机器人分解为两个3R 子链后用微分流形来求解机器人逆运动学的方法。卜王辉等[21]在文献[18-20]的基础上，对腕部前端偏置型机器人进行了研究，给出了机器人分解为两部分时选择切断点的建议，但其分析方法具有局限性，且变换方程的推导过程过于复杂。

在文献[17-21]研究的基础上，针对几款常见的6R 非球腕工业机器人，本文提出多切断点分解—重构技术推导其逆运动学公式。基于旋量理论的指数积公式建立机器人的正向运动学公式，得出机器人可分解的结论；给出切断点的选择和重连的几何约束条件；仿真实验证明了本文所提方法的有效性。

1 n 自由度机器人的分解

研究机器人运动学的学者中，大多使用DH 方法[22]建立正向运动学公式，然后通过矩阵的逆乘找到可以求逆解的方程。事实上，这其中已经包含了将机器人分解的思想，由于DH 法不具备直观地几何意义，从而导致该思想没有被提炼出来。旋量法中的Paden-Kahan 子问题[1,23]也包含了机器人分解的思想，但是该方法在做公式变形时，只考虑了分解点的位置，而忽略了分解点的姿态信息。

1.1 n 自由度机器人运动学的旋量表示

旋量理论[24]将刚体在空间的运动描述为由绕某一定轴的旋转和平移复合而成。设ω=[ωx ωy ωz]T∈R3表示刚体旋转轴的方向，r为轴上一点的位置，则刚体的运动旋量可用ξ=[ωv]表示，其中v=r×ω，ξ同样可以被称为刚体的螺旋轴。ω的反对称矩阵记为

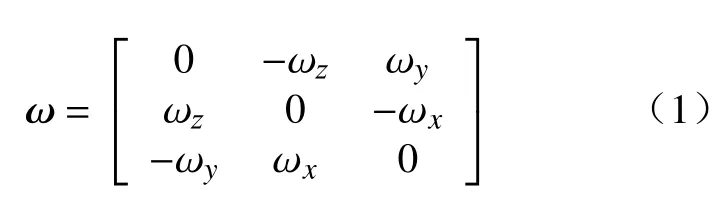
以反对称矩阵为推广，可将ξ的矩阵形式记为

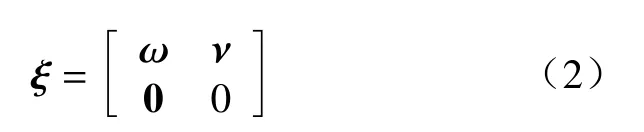
刚体的矩阵指数形式为

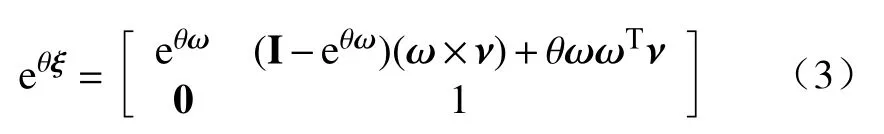
式中eθω=I+ωsinθ+ω2(1-cosθ)。

图1 为n自由度机器人。

图1 n 自由度机器人

根据旋量理论，图1 中n自由度机器人的正向运动学公式的指数积表达形式为

式中：gST(θ)为经刚体变换后机器人末端工具坐标系{T}为相对于惯性坐标系{S}的位姿gST(θ)；gST(0)为机器人位于初始位形时工具坐标系{T}相对于惯性坐标{S}的位姿。

各关节轴旋转的正方向规定为右手拇指指向关节轴线时，四指弯曲的方向。

1.2 n 自由度机器人可分解说明

式（4）可变形为

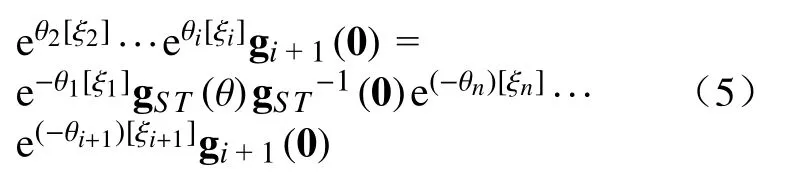
式中gi+1(0)是一个位姿矩阵，由于位姿矩阵始终可逆，故等式两边同时约去它亦可保持相等。若gi+1(0)的位置位于连接关节i至关节i+1 的连杆之上，则等号两边的式子将具有直观的几何意义，表示原机器人分为两部分子链。

图2 中{Ti+1}为建立在关节{i+1}原点上的坐标系，其相对于原世界坐标系的位姿矩阵为gi+1(0)。由式（4）的形式可知，式（5）等号左边的式子表示关节Link1左侧端点至Linki端点组成的子链，图2 上部，需要注意的是，关节1 此时与Link1已断开；式（5）等号右边的式子，则表示关节1 与关节n至关节i+1 所组成的子链，其中关节1 与Linkn末端由虚拟连杆连接，该虚拟连杆由gST(θ)gST-1(0)的值决定。

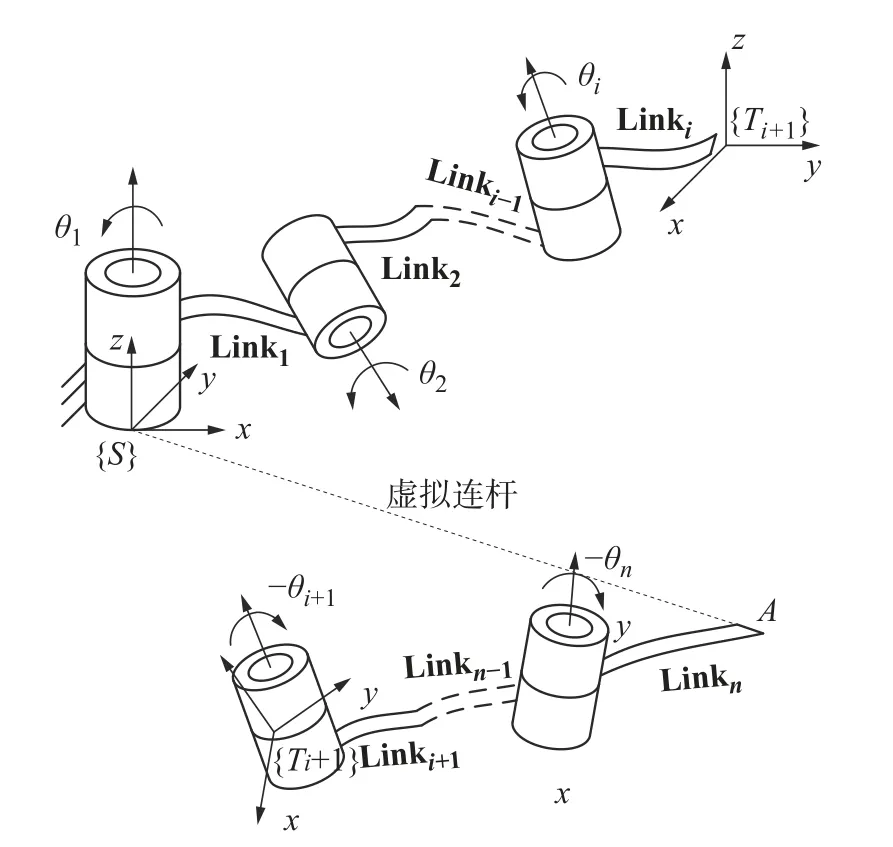
图2 机器人分解图

因此式（5）等号两边的式子表示在关节1 和关节i+1 的原点分别进行了切断，并重新连接组成了两个新的子链，为方便理解，记关节1 处为切断点1，关节i+1 处为切断点2，不含虚拟连杆的子链记为子链L，含虚拟连杆的子链记为子链R。值得注意的是，子链R中关节角前面加负号，表示与原机器人对应关节角的旋转方向相反。

子链的工具坐标系{i+1}可以任意设定。为了简化后续逆运动学公式的推导，给出以下原则：

1）切断点优先选择在关节的原点；

2）位于切断点1 处的两子链的基座标系，尽量与原机器人惯性坐标系一致；

4）工具坐标系{i+1}应有一条轴线与所在切断点关节的轴线共线或平行；

5）分离得到的子链中，决定末端位置的关节数和决定条件4）中轴线方位的关节数应同时最少。

此时，两个子链重新结合为原机器人的通用几何约束为末端执行器的位姿重合。

2 机器人的分解及逆运动学求解

本节将以文献[21]中的MOTOMAN-EA140型6R 机器人为例求逆解，该机器人手腕存在30 mm的前端偏置。

2.1 正向运动学

图3 中选择{S}作为惯性坐标系，{T}作为工具坐标系，{T}与螺旋轴的参数均以{S}为参考描述，且{T}的原点与关节6 的原点重合。

机器人零位时工具坐标系的位姿为

实验的设计对象是水杯产品。水杯较常见，其复杂程度低、易于表现、设计周期短，但是创意空间较大。水杯的评价指标以单一的感性因素为主，避免了多目标评价的复杂因素影响。

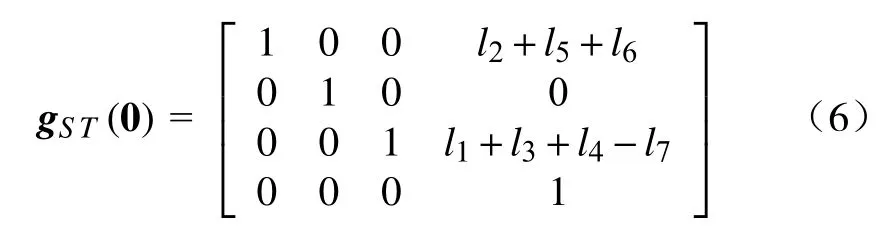
各关节螺旋轴参数列于表1 中。

表1 各关节螺旋轴参数

MOTOMAN-EA140 机器人的正向运动学公式为

2.2 分解

根据2.1 的分离原则，可将式（7）变形为

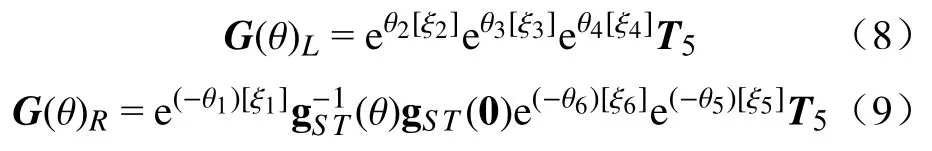
其中

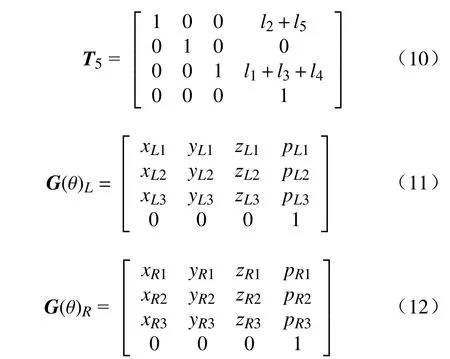
从图4 可以明显看出，子链L的末端位置以及工具坐标系的xL轴只由关节2、3 决定；子链R的末端位置以及工具坐标系的yR轴只由关节1、6 决定。而该几何结果，同样可从式（8）和式（9）的结果中反应，将表1 中螺旋轴参数代入式（11）和式（12）中，得

图4 MOTOMAN-EA140 机器人分解图

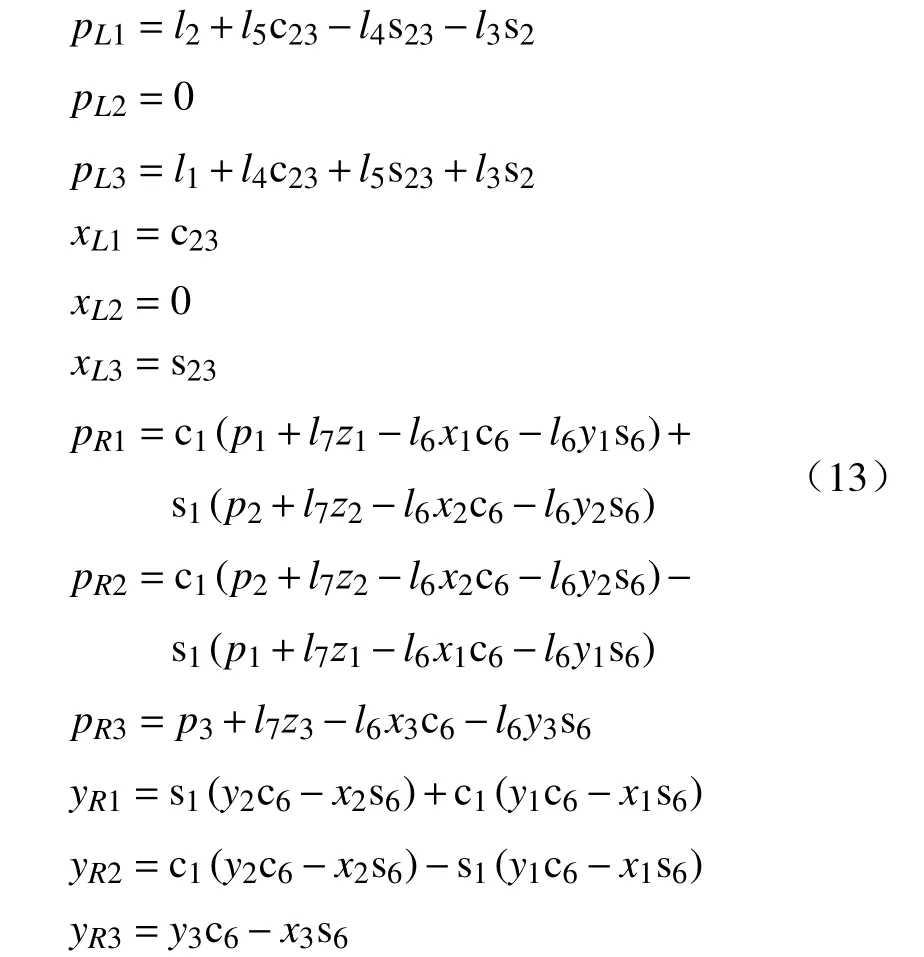
式中：si=sinθi；ci=cosθi；sij=sin(θi+θj)；cij=cos(θi+θj)；i、j=1,···,6，且i≠j。

2.3 逆运动学求解

由子链重新结合的通用约束条件可知pL=pR。

首先由pL2=pR2可直接得到θ1关于θ6的表达式为

其中

将pL1=pR1、pL3=pR3联立为方程组，并将等号右边的常数项均移至等号左边，然后平方求和，得

将已求得的θ1和θ3代入pL1=pR1、pL3=pR3组成的方程组中，可得

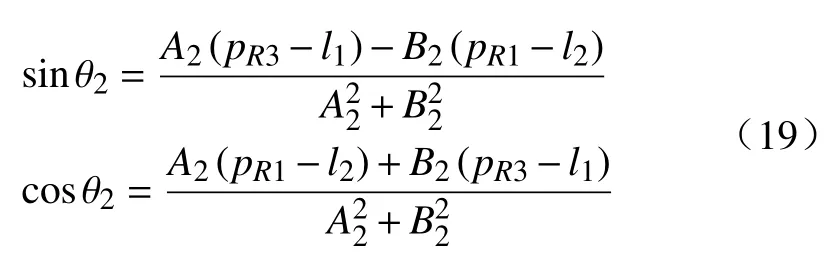
其中

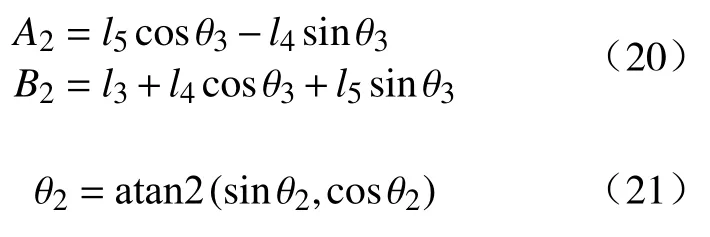
至此可以得到θ1、θ2和θ3关于θ6的表达式，由式（14）和式（17）可知θ1、θ2和θ3将有四组解。

由2.2 节可知xL与yR分别由θ2、θ3和θ1、θ6决定，而两个子链末端工具坐标系重合是必要的约束条件，故xL⊥yR，即xL·yR=0，因此可得关于θ6的封闭方程为

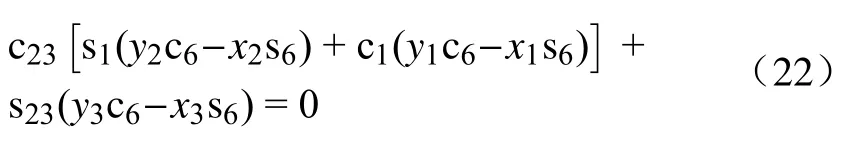
从前面θ1、θ2和θ3解的组数可知，方程（22）也将有4 个。一旦求出θ6，即可反代回式（14）～ 式（21）求出θ1、θ2和θ3，然后利用子链姿态矩阵相等，可以求出θ4、θ5。

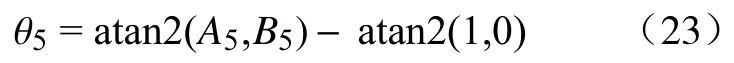
其中

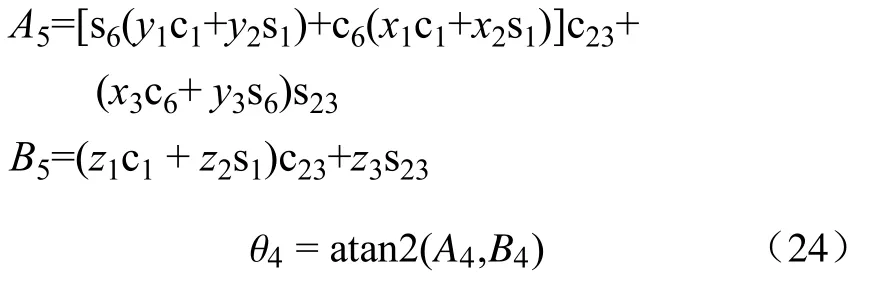
其中

2.4 二分法求解

方程（22）是关于θ6的非线性方程，直接求解很困难，本文使用二分法[25]对其搜索求解。将式（20）改写为关于θ6的函数

此时只需求出式（26）中的零点，因求解过程中均为数值解，故只需求使得|f(θ6)|≤ε的θ6即可，ε为设定的算法终止阈值。求解方法如下：

1）初始化θ6。θ6的迭代步长h，阈值ε；

2）确定区间。将θ6迭代的数值代入式（14）～ 式（21）和式（26），若θ6k=θ6k-1+h，则确定二分区间为[a,b]，a=θ6k-1，b=θ6k，否则继续迭代，直至θ6k≥2π 停止。在此搜索过程中，若|f(θ6k)|≤ε，同样停止迭代，输出θ6k。

3）求区间[a，b]中点c。（1）计算f(c)，若|f(c)|≤ε则停止；（2）若f(a)f(c)＜0，则令b=c；（3）若f(c)f(b)＜0，则令a=c；（4）若达到阈值ε，则输出a或b，否则继续重复1）～3）。

3 仿真算例

算法的计算软件为MATLAB2014b，PC 配置如下：处理器为Intel(R) Core(TM) i7-9750H，CPU 速度为2.60 GHz，安装内存为16.00 GB。算法文件格式采用.m 函数编写，再使用MATLAB Coder 转换为mex_fun 格式。

图3 中MOTOMAN-EA140 机器人的连杆参数分别为l1=450 mm，l2=150 mm，l3=570 mm，l4=200 mm，l5=640 mm，l6=30 mm，l7=20 0mm。二分法参数设置为：θ6(0)=0，ε=10-14，h=π/180。

设定目标位姿为

式（26）与其对应的图形如图5 所示。图中4 条曲线分别对应式（26）的4 组函数，图中明显可见，黄色“--”与蓝色“-.”曲线分别有4 个零点，其它两条曲线各有2 个两点，因此位姿T共有12 组解（见表2，表中e为逆解代入正向运动学得到的位姿与T的误差二范数）。在MATLAB 中采用mex_fun 函数编写二分法，得到图中所有解的时间约为2 ms。其中有4 个零点的曲线比只有2 个零点的曲线约多花费1/3 的求解时间。

表2 目标位姿T 的12 组逆解

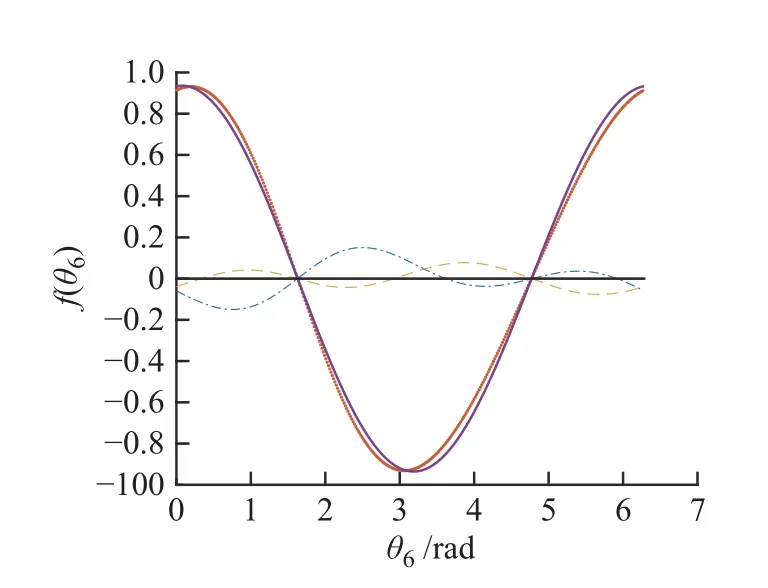
图5 位姿T 对应的f(θ6)曲线

本文所使用二分法的总体时间与步长h的取值有关，步长越大则消耗的时间越少，但如果f(θ6)函数的零点距离很近，则可能会遗漏掉部分解。同时，零点个数的多少也对求解时间有影响，零点越多，消耗的时间也越多。

因本文此次研究的重点在于逆运动学公式的推导，故在仿真中没有与其它算法的求解效率作比较，仅提供了一个解决式（26）的选择方案。

值得注意的一点，将机器人的手腕偏置设为0，则本文所罗列的公式即为球腕机器人的解析解公式。

4 结论

1）通过对机器人正向运动学的指数积表达式变形，说明了任意机器人可分解为两个低自由度子链的可行性，并描述了各式子的几何意义。给出了机器人切断点的通用原则，以及子链重新结合的通用约束条件。

2）在手腕具有前端偏置的工业机器人的关节1 与关节5 原点处切断，得到了2 个子链，其中子链L 的工具坐标系只具有平面运动效果，两个子链的正向运动学式子更为简洁。其它非球腕工业机器人，也可借鉴该切断方法推导逆解公式。

3）根据子链重新结合的几何约束条件，简化了各关节逆运动学推导的过程，并得到了关于θ6的一元非线性封闭方程，该推导过程具有明确的几何意义。

4）为求解一元非线性方程提供了一种方案，二分法得到目标位姿所有逆解的时间约为2 ms，计算位姿误差为10-12mm。