工业机器人关节振动的鲁棒扰动观测器双环补偿控制

罗宝佳，吴震宇，詹明儒

（1.湖北工业大学 机械工程学院，武汉 430068；2.贵州民族大学 机械电子工程学院，贵阳 550025）

RV 减速机是重载关节型工业机器人3 大核心部件之一，在机器人的关节处，由其将伺服电机的动力传递给机械臂。自动化生产线不仅要求机器人具有很高的精度而且还要运行平稳，然而，由于加工、装配以及润滑的要求，减速机齿轮副之间难免存在间隙，这些间隙不仅会影响减速机的传动精度，还会引起系统的振动。所以，无论是生产厂家还是科研院所都希望能够通过对摆线齿轮修形技术、齿轮啮合理论、装配工艺以及零件检测的研究，提升减速机的传动特性[1-4]。尽管提升核心部件的性能是保证机器人高质量运行的必要手段，但同时伺服电机、减速机以及负载构成了完整的机电耦合系统，该系统的运行性能还与系统控制有很大的关系。因此，不仅要从改善部件质量的角度提升系统性能，还要从系统控制的角度去改善机器人的运行平稳性。

Tungpataratanawong 等研究了二惯量工业机器人，提出了一种利用系统共振参数辨识进行振动控制的方法[5]；Yoshioka 等建立了工业机器人的角传动误差模型，并采用扩展状态观测器对误差进行补偿[6]；Kosaka 等提出以状态空间扰动观测器对扰动以及其它状态变量进行估计，在低刚度系统中取得了较好的效果[7]；Kumagai 等采用无相位延迟的零相位陷波滤波器对工业机器人的运动轨迹进行快速跟踪，并在此基础上采用D-PD 的动态前馈补偿来抑制振动现象[8]；Kamel 等采用输入整形的方法对系统响应的延时进行补偿，从而提高系统稳定性[9]；Yeon等提出了一种迭代学习控制方法，并通过实验验证了该方法的有效性[10]；Munoz-Vázquez 和 Gambhire等都采用滑模-对运动轨迹进行快速跟踪控制[11-12]；Hendzel 等提出了一种鲁棒神经网络运动跟踪控制方法，对非线性的对象进行控制，并取得了较好的控制精度[13]。工业机器人关节处的传动系统有其特殊性：一是同时存在间隙和摩擦因素的影响；二是受到安装条件的限制，不便于采集负载侧信号作为反馈控制变量。研究对象的这些特殊性也会影响控制方法的使用效果。上述方法虽然能够在一定程度上解决工业机器人的速度波动现象，但是依然存在一些问题，迭代学习控制需要确定合适的收敛算法；共振参数辨识对参数变化快的系统需要时间较长不能保证实时性；滑模控制中滑模轨迹进入死区后，运动轨迹不可控制，造成抖振现象；神经网络对非线性系统的辨识需要较多的训练次数才能达到理想的逼近精度；陷波滤波器的频带太窄只能消除很小范围内的扰动频率。本文在外环扰动观测器中加入低通滤波器环节抑制信号采集过程中测量噪声，弥补了陷波滤波器抑制噪声频带范围较窄的不足；而且采用扰动观测器能够实时地对误差进行补偿，避免了共振参数辨识的时间延迟效应；另外，本文针对RV 减速机啮合刚度和传动误差等参数的时变性，采用鲁棒控制理论提高了控制系统的适应性。

本文提出一种基于鲁棒互质分解和扰动观测理论的双环控制策略，对由伺服电机-RV 减速机-负载所构成的机电耦合系统进行抑振。首先，建立了考虑动态角传动误差和啮合摩擦激励影响的机电耦合系统模型；在此基础上，采用内环右互质分解理论对速度波动进行一次补偿；为了消除内环补偿过程中噪声干扰以及时变因素，如时变刚度，对速度补偿效果的影响，进一步采用外环扰动观测器控制方法对负载侧转速进行二次补偿。在内、外环控制环节，都要用到负载侧转速作为反馈变量。但是，受到空间和工作条件的限制，很难在机器人负载侧安装传感器用于采集控制所需要的数据。因此，本文通过构建状态观测器得到了负载侧转速的估计值。最后，通过仿真和实测数据验证了本方法有效性。

1 电机-减速机-负载耦合系统模型

工业机器人关节处，由电机-减速机-负载组成如图1 所示的机电耦合系统。本节在减速机动态传动误差激励分析的基础上，建立了考虑减速机齿轮副摩擦因素影响下的工业机器人关节处的机电耦合系统状态方程。

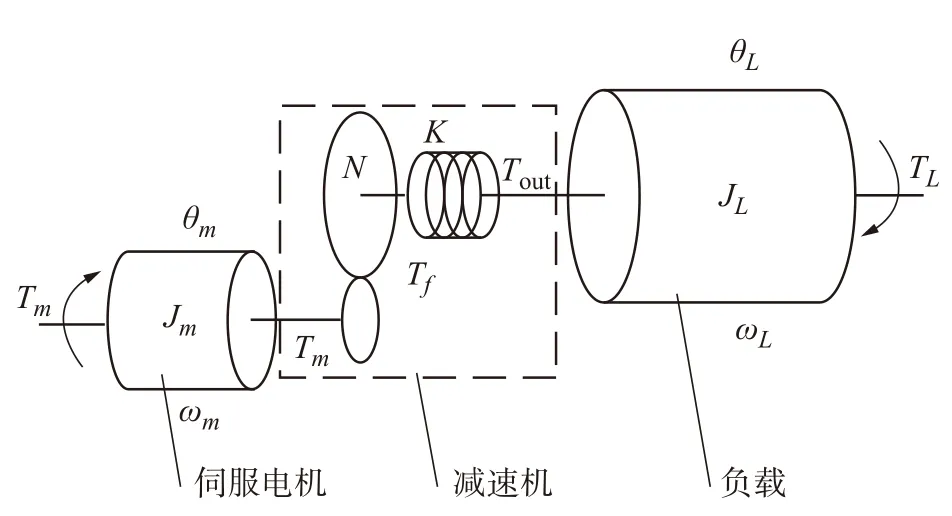
图1 工业机器人关节处机电耦合传动系统

1.1 动态角传动误差模型

减速机不可避免存在角传动误差，即当输入轴转动一定角度，此时输出轴在理论上的转角与实际转角的角度差值，其表达式为

式中：θ1(t)为输入转角；θ2(t)为输出转角；N为传动比。

理想状态下，RV 减速机的摆线齿轮与针齿之间为完全啮合，整个系统为刚性连接，但是由于加工和安装误差以及摆线轮修形的要求，使啮合齿廓偏离理想啮合位置，破坏了正确啮合方式。因此，传动比N并不是恒定的，而是瞬时变化的。由式（1）可知，如果传动比N出现瞬态且不确定性变化，传动误差TE必然也会出现波动。图2 为RV40E 减速机角传动误差实测数据，验证了上述分析，能够看出实测数据有一个大致的变化范围，但是在这个变化范围内，传动误差又是上下波动的。对其进行FFT变换，如图3 所示。

图2 角传动误差实测数据

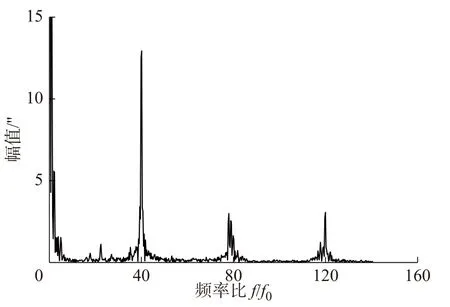
图3 角传动误差的幅频特性

f0为负载侧的转动频率，=40 的位置对应角传动误差的基频 ωb，而且基频 ωb与负载侧的输出转速 ω0的比值“40”等于减速机针齿齿数Np，即

又因为

所以

式中 ωm为伺服电机的角速度。

图2 的动态角传动误差可以写成傅里叶展开式的形式为

式中：Ak为角传动误差的振动幅值；φk为角传动误差各振动成分的相位。

由式（5）可知，动态角传动误差数学模型中，基频大小取决于RV 减速机针齿齿数。在机器人关节处选用不同型号的RV 减速机，只要确定了其针齿齿数，就可以得到角传动误差的波动基频。

1.2 摩擦力矩模型

RV 减速机工作过程存在摩擦损耗，只有通过控制电机对摩擦转矩进行补偿，才能驱动负载在规定的转速下运转。本节建立摩擦力矩模型的目的就是为了在后续控制器的设计中，能够用前馈补偿算法来消除摩擦的影响。

目前，在机械运动系统中常用的典型摩擦模型有动态摩擦模型，如LuGre 摩擦模型[14-15]和Dahl 摩擦模型[16]等。但是动态摩擦模型会引入一些难以测量的参数，增加了建模难度。此外，还有库伦摩擦模型、库伦+粘滞摩擦模型、静摩擦+库伦+粘滞摩擦模型、Stribeck 摩擦模型等静态模型[17-19]。选用不同的摩擦模型取决于研究对象经历的工作时间段，例如库伦摩擦模型只能描述研究对象从启动到稳态运行这段过程中所受到的滑动摩擦力。就工业机器人用RV 减速机特定的工作过程而言，在RV 减速器启动瞬间，主要受接触面间正压力产生的静摩擦力；从开始转动到稳态运行的过程中，主要受正压力产生的滑动摩擦力，以及接触面与油膜相对运动产生粘滞摩擦力；当RV 减速机平稳运行后其摩擦主要为滑动干摩擦。综上，减速机从静止启动到稳态运行的全过程中，承受了不同类型的摩擦力。在众多静态摩擦模型中，Stribeck 模型能够反映不同阶段的摩擦特性，而且相比复合型摩擦模型，如库伦+粘滞摩擦模型、静摩擦+库伦+粘滞摩擦模型，更加方便使用。因此，本文选用Stribeck 摩擦模型来描述RV 减速机在整个运动过程中所受到的摩擦力矩[19]，数学模型为：

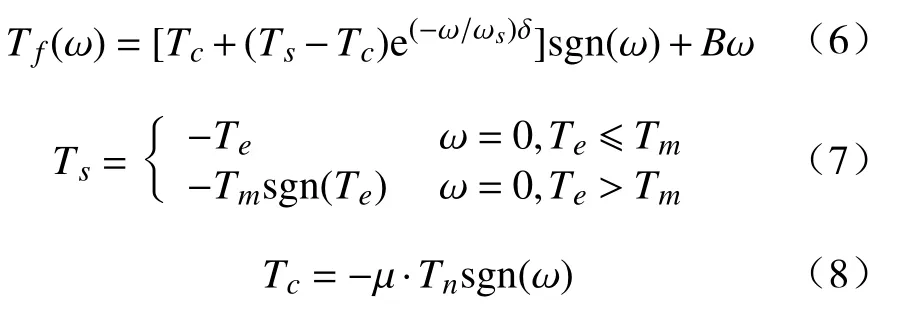
式中：Ts为减速机未发生转动时的静摩擦力矩；Te为外力矩；Tm为最大静摩擦力矩；Tc为库伦摩擦力矩；Tn为接触面的力矩；ωs为Stribeck 速度；B为黏性摩擦因数；ω为摩擦面的相对速度；δ为Stribeck 模型常数，δ=1；µ为摩擦因数。

1.3 机电耦合系统动力学模型

在确定了动态角传动误差激励和摩擦力矩的基础上，对图1 所示的由伺服电机、RV 减速机以及负载组成的机电耦合系统列动力学方程为：

式中：Tm、θm和Jm分别代表伺服电机的转矩命令值、位置和转动惯量；Tin、Tout代表RV 减速器的输入转矩和输出转矩；K和Tf分别代表减速器的刚度和摩擦力矩；JL、θL和TL分别代表负载的转动惯量、位置和负载转矩；为电机的电枢电流；Kt为电机常数。

原始系统框图如图4 所示，仿真时加入了角传动误差以及非线性摩擦。

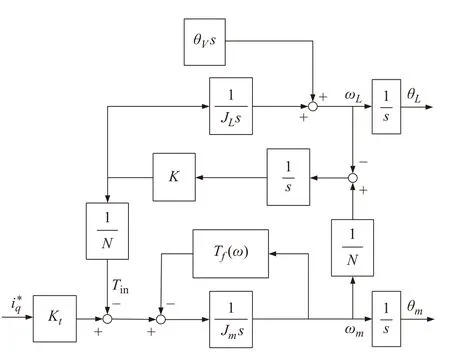
图4 原始系统框图

由动力学方程求得系统在电机转速为780 r/min以及传动比为121 的情况下，负载侧的响应如图5所示，可以看出，系统的稳态响应在均值0.67 rad/s附近存在明显的波动。因此，对于要求工作精度极高的自动化生产线而言，必须采用有效的控制方法抑制系统的振动。

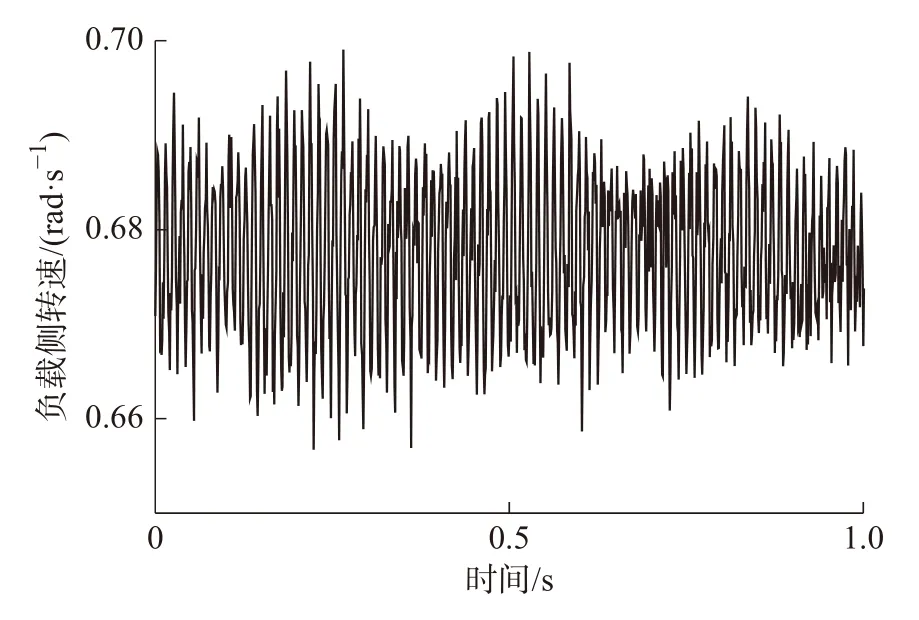
图5 原始系统负载侧的振动响应

2 二次鲁棒补偿控制系统设计

采用内环+外环的双环控制策略对机器人关节处负载侧的转速波动进行实时补偿。其中，内环控制是基于鲁棒控制的右互质分解理论[20]；外环控制则是基于扰动观测器理论[21]。下面将结合图6 所示系统框图，对该系统进行详细说明：

图6 控制系统框图

首先，本文定义了两个系统Pn(s)和P(s)，Pn(s)为假设不存在减速机角传动误差而且没有摩擦的理想状态下的耦合系统；P(s)为考虑了摩擦力矩和角传动误差影响的实际耦合系统。

由于真实的耦合系统P(s)与假想系统Pn(s)存在差异，因此，如图6 所示，先采用内环控制对转速波动进行一次补偿，其中X(s)和Y(s)可由鲁棒控制的右互质分解理论对Pn(s)进行分解求得。是由电机转速 ωm和电机输入电流i经状态观测器后得到的负载侧转速的估计值，目的是为了解决负载侧不便于采集转速信号作为反馈变量的实际困难。

但是在内环控制过程中，一方面采集的信号会存在测量噪声，影响内环速度补偿的精度；另一方面，系统中一些参数并不是定值，而是时变参数，例如负载转动惯量JL随转动位置的变化而变化，减速机的刚度K也是时变的，这些参数的实时变化很难在建模过程中得到真实反映，所以内环一次补偿控制不能完全消除转速波动，需要再通过一次外环控制来消除噪声干扰以及时变因素对控制效果的影响。

在外环控制中，输入电流I经理想系统Pn(s)得到负载侧理想输出转速 ωnL，与状态观测器得到的负载侧转速估计值进行比较，得到理想状态下的输出转速与经过内环补偿后的输出转速的差值d。

由于在内环控制中，电机转速的采集信号 ωm包含电机的实际转速和测量噪声 β，因此，由观测器估计得到的负载侧转速中仍然包含噪声成分，所以理想系统Pn(s)的输出 ωnL与负载侧转速估计值 ωˆL的差值d，仍然含有噪声成分，因此要串联一个二项式低通滤波器Q(s)，得到降噪后的转速差dn。

再根据扰动观测器理论，经Pn(s)-1环节，将dn转换成电流补偿值δ，并将其补偿至参考输入电流I*中。

对本文方法的有效性证明如下：

将内环补偿后的系统用Pe(s)表示，如图7 所示。

图7 内环 Pe补偿后的系统框图

可以得到补偿电流δ 为

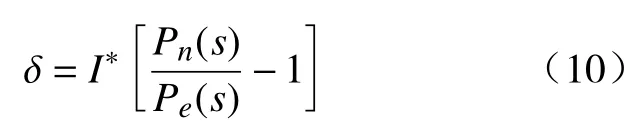
将δ 补偿至参考电流I*中，得到输入电流I为

输入电流I经系统Pe(s)，得到负载侧输出为

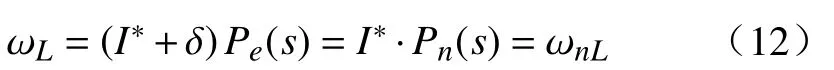
由式12 可知，经双环补偿控制后的负载侧输出ωL与理论输出 ωnL相等，因此可以证明双环补偿策略可以消除转速波动。

3 性能测试

3.1 状态观测器性能测试

首先判断系统的可观测性，根据判别式（13），可知系统可观测。

将状态观测器设置为

状态观测器极点配置在-420±6i、-300 位置，保证状态观测器有良好的收敛效果。通过状态观测器的得到的系统转速与实际转速，以及误差如图8所示。由图可以看出系统的观测转速与实际转速的误差在 ±4%范围内，因此该状态观测器可以对负载测转速有很好的观测效果。

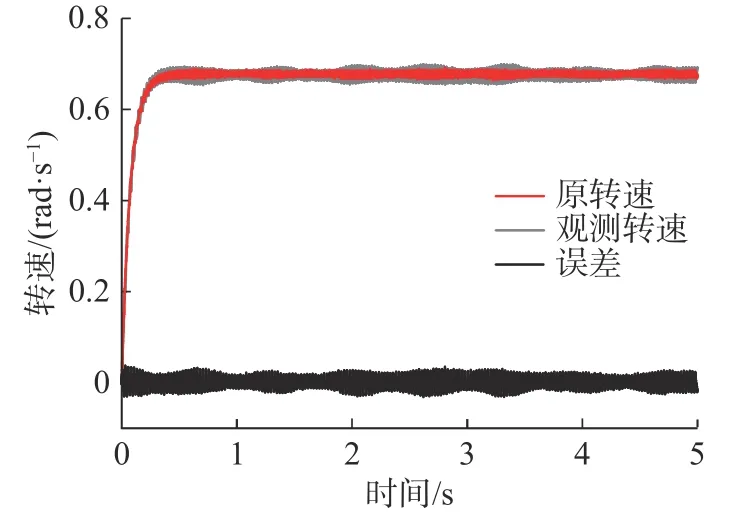
图8 观测误差

3.2 仿真验证

通过仿真验证本文方法的有效性，系统参数如表1 所示。

表1 机电耦合系统参数

对比工业常用的PI 控制方法以及本文提出的控制方法的负载侧速度响应，如图9 所示。

图9 负载侧速度响应仿真对比

PI 控制的速度响应达到稳态的调节时间为0.21 s，而本文提出的控制方法的调节时间为0.29 s，两种方法几乎一致。但是从图中可以看出PI 控制在达到稳态之前有明显的超调，这种急加速再急减速的变化会使得负载侧产生剧烈的冲击和振动；相比之下，本文方法在保证响应速度的同时，还能够使系统比较平稳地达到稳定状态。接下来，对稳态响应的幅频特性进行比较，如图10 所示，本文方法相比PI 控制，在频率比为40 和80 处的振幅得到了明显地削弱，由原来的0.005 8 rad/s 降为0.000 7 rad/s，转速波动现象基本消除。通过上述仿真结果，可以证明本文方法不仅使机器人的负载侧能够快速且平稳地实现指令，而且负载侧在稳态运动过程中的速度波动现象也得到了极大的改善。

图10 负载侧速度响应的幅频特性仿真对比

3.3 试验验证

试验装置如图11 所示，采用卧式传动，磁粉制动器用于模拟机器人的加载过程，采用日本Nabtesco RV-80E 型减速机，在此基础上建立以TSM320F 28335DSP 为核心的控制系统，分别通过HOP-18000-D90-2 高精度编码器和霍尔传感器采集伺服电机转速和电流信息，用于状态观测器对负载侧的转速进行 估计。

图11 试验装置

经PI 控制和本文方法控制后的负载侧实测速度信号，如图12 所示。从时域速度波形图可以看出，采用PI 控制的速度波动范围为0.687～0.659 rad/s，采用本文控制方法其速度变化范围为0.678～0.665 rad/s，由幅频特性可以看出在频率比为40 和80 处，本文控制方法相比PI 控制其幅值分别减小了51.6%和51.2%，因此，本文提出的控制方法能够有效地降低负载侧的转速波动。

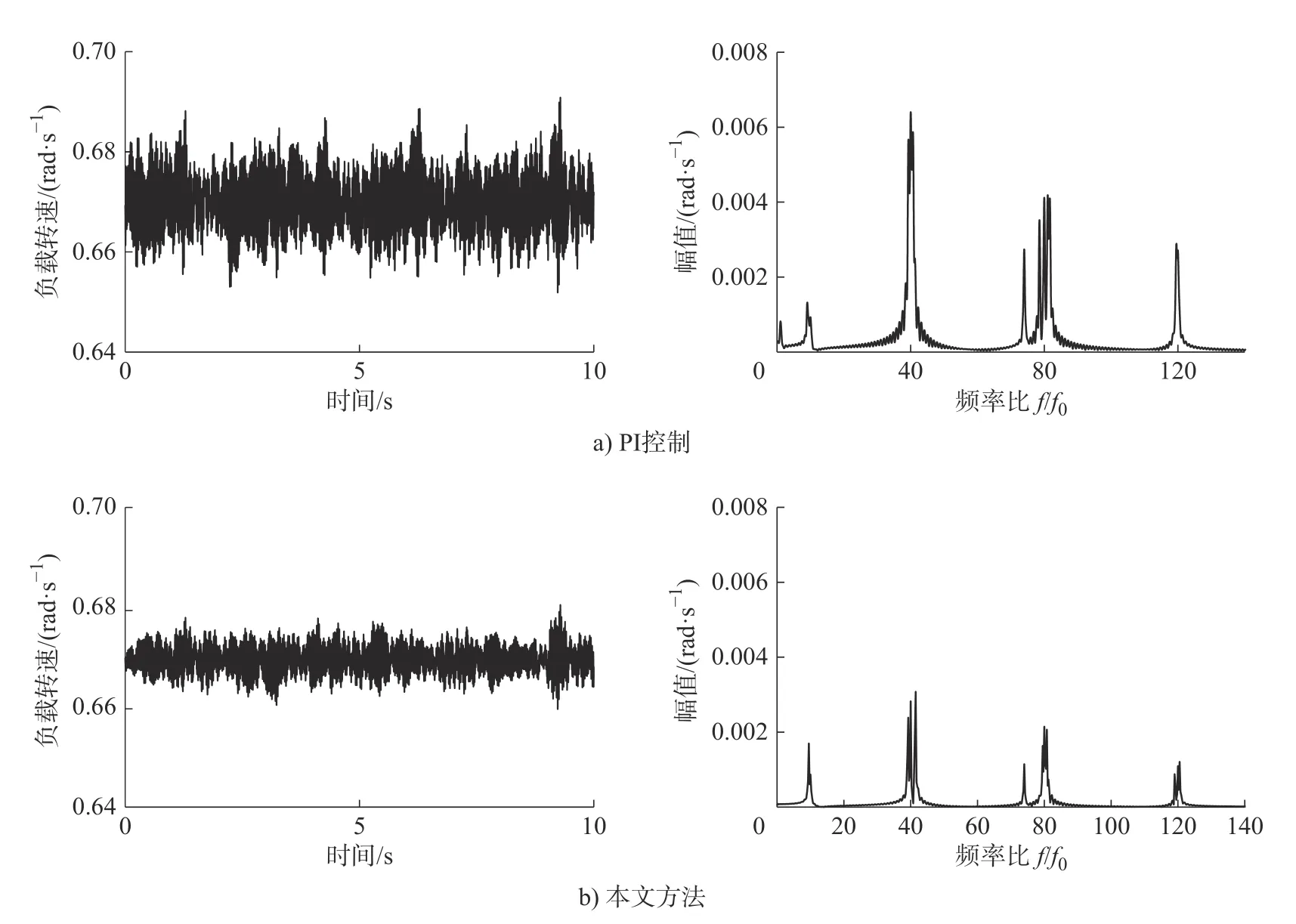
图12 实测数据对比

4 结论

1）根据实测的角传动误差数据，建立了动态角传动误差的数学模型。发现在同等工作条件下，动态角传动误差基频大小只取决于RV 减速机针齿齿数。

2）建立了考虑动态角传动误差以及摩擦因素影响的电机-RV 减速机-负载所构成的机电耦合系统动力学模型。研究发现减速机刚度降低、传动误差以及啮合摩擦是引起负载侧转速波动的主要原因。

3）采用内环+外环的双环控制策略对机器人关节处负载侧的转速波动进行实时补偿。该方法在理论上可以完全消除负载侧的转速波动，相比PI 控制，该方法能够更加有效地抑制机器人负载侧的转速波动，满足精准控制的使用要求。