一种仿象鼻气动连续体机器人的结构设计
2022-05-14张启航邵敏任树雄贺晶奎王晶
张启航,邵敏,任树雄,贺晶奎,王晶*,
(1.西安交通大学 机械工程学院,西安 710049;2.西安交通大学 工程坊,西安 710049)
机器人是综合多学科先进技术于一体的智能机器,相比传统刚性杆件机器人,柔性机器人具有多项明显的优势,例如可以与环境实现安全交互、在受限空间内实现灵巧操作以及抓取非结构化物体等,因而在最近十余年成为了研究热点[1]。连续体机器人是一种新型仿生机器人,它模仿自然界中象鼻、章鱼臂等动物器官的运动机理,自身不存在离散关节,但能依靠连续柔性变形来实现运动操作,其驱动方式包括弹性杆/线驱动[2-6]、形状记忆材料驱动[7]和气压驱动[8-9]。连续体机器人的研究主要是针对仿蛇机器人,但由于没有系统的理论导致其结构设计缺乏指导,加上机器人的变形和运动难以控制,当时并未得到广泛关注。1982 年,Larson 和Davidson 设计了一种连续体机器人用来完成汽车的喷涂工作,连续体机器人首次出现在工业应用领域。20 世纪90 年代,设计出仿人手指机器人[10]、KSI 触手型机械手[11]等连续体机器人。2011 年,FESTO 公司研发了“仿生搬运助手”,该结构轻巧灵便,可以安全平稳的完成各种动作[12]。克莱门森大学的Walker 团队对连续体机器人展开了系统研究[13-16],研究范围涉及各种不同驱动方式的连续体机器人,如Air-Octor机器人、仿章鱼触手的机器人(OctArm)等。2017 年,在“仿生搬运助手”的基础上,FESTO 公司推出了更加柔顺、负载能力更强的气动连续体机器人——Bionic motion robot,又研发出了模块化气动轻型机器人——Bionic soft arm。2021 年,Boettcher 采用模块化设计方法设计了由3 个肌腱并联驱动的连续体机器人,该机器人具有良好重复性[17]。
2015 年,徐凯基于多杆连续体机构设计了一种外骨骼辅助康复机器人,该机器人可以自适应患者的不同肌骨,帮助患者恢复肢体的功能[18]。2018年,康荣杰教授团队采用记忆合金驱动设计了一种连续体机械臂,可以实现变刚度和良好的运动控制[19]。2020 年,廖兵利用可折叠波纹管设计气体驱动的仿蛇缠绕软体爬杆机器人,可应用于高压电缆和管道的巡检工作[20]。
本文对连续体机器人的结构及设计参数进行了深入研究,进一步说明串联与并联结构在机器人结构上的广泛应用。
1 设计目标与整体设计方案的确定
1.1 仿象鼻连续体机器人的设计目标
参考大象搬运物体的过程,设计的气动连续体机器人应当能够实现以下3 个目标:
1)仿象鼻气动连续体机器人能够完成伸长、弯曲和偏转变形,并控制末端在相应空间内实现自由运动。
2)机器人末端能够实现抓取和放下物体,可以完成搬运物体的工作。
3)仿象鼻气动连续体机器人的运动状态应当可以被反馈,这是实现机器人闭环控制的必要条件。
1.2 连续体机器人整体结构设计方案
连续体机构最小运动单元被称为构节。一个构节通常由一个基座盘,一个末端盘,若干间隔盘以及若干驱动杆组成。构节通用结构见图1。
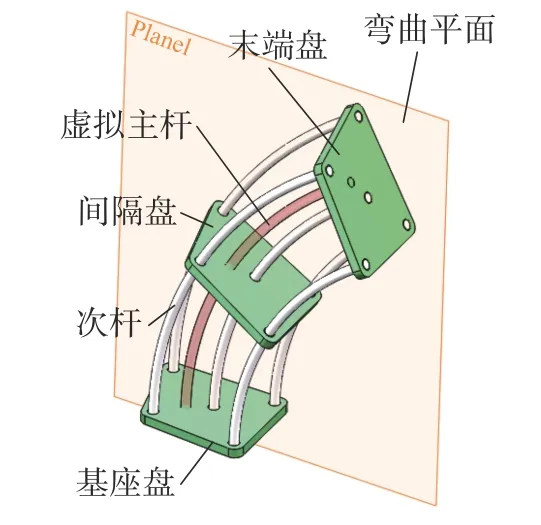
图1 连续体构节结构化简图
连续体构节的驱动杆通常为3 到4 根,既保证了有效的驱动又不至于使系统过于复杂。构节中引入间隔盘可以通过约束驱动杆和连续体构节的变形,使连续体构节的变形更加可控。单个连续体构节可以实现两种变形:伸长(或缩短)变形和弯曲变形。对于多构节串联机构,当各构节的弯曲平面不重合时,机构将发生偏转。
从表1 可以看出,多构节连续体机构与象鼻在各个变形能力方面比较接近,在伸长变形方面,多构节连续体机构比象鼻更加优秀。因此仿象鼻机器人的整体设计方案采用多个连续体构节串联方式,单个构节设计成3 个驱动杆(气动肌肉)120°均布的并联结构,并附加若干间隔盘。
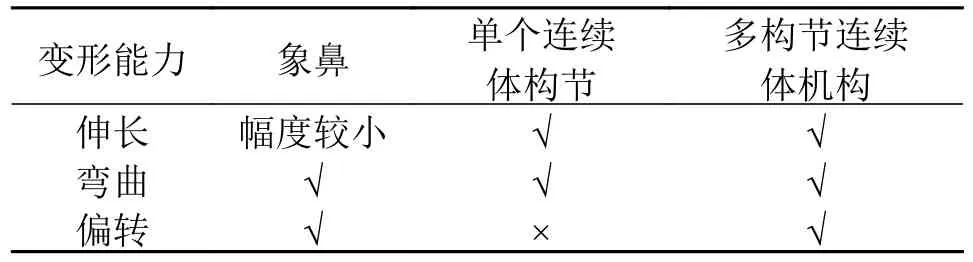
表1 象鼻、单个连续体构节和多构节连续体机构变形特性
2 仿象鼻气动连续体机器人结构设计
2.1 气动肌肉设计
气动肌肉是一种特殊的气动执行器,通过内部气压的变化使自身伸长或缩短。在McKibben 型肌肉基础上设计一种新型气动肌肉,如图2 所示。该气动肌肉用到的波纹管主要参数见表2。橡胶波纹管具有良好的柔性,从某一端盖通入压力气体时,由于限径圆环限制了气动肌肉径向的扩张,其只能在轴向上发生伸缩。这种气动肌肉能够方便的安装成构节形式,而且具有较大的伸长率,非常适合于作为气动连续体机器人的驱动器。

图2 气动肌肉实物图

表2 波纹管参数表
2.2 单构节结构设计与构节数目的确定
设计的气动连续体构节采用3 个气动肌肉并联,其中心均布在半径为r的圆上,见图3。单个构节仅具有3 个自由度,将连续体构节进行串联,就可增加自由度数量和机器人的灵活度及可操作度。采用常曲率方法[21]可建立多构节连续体的近似运动模型,进一步可推导出雅可比矩阵J。下面从工作空间、奇异性、操作度和条件数几个方面研究构节数目对连续体机器人的影响。
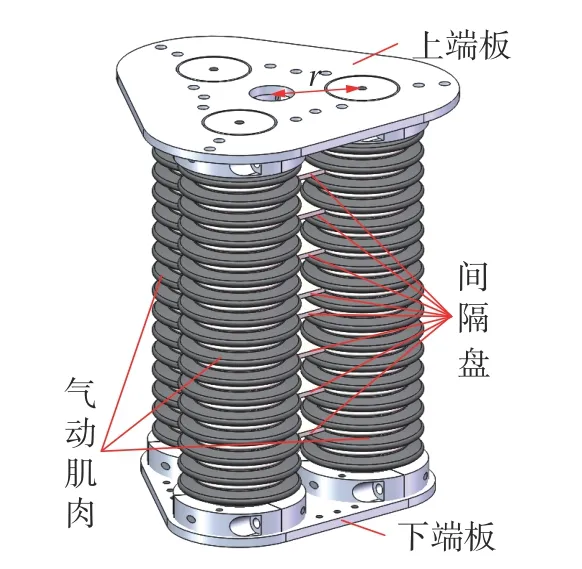
图3 单个构节三维模型图
1)工作空间分析
连续体构节不存在可分辨的离散关节,不适合使用解析法,故采用穷举法和蒙特卡罗法[22],结合常曲率模型计算连续体机器人的工作空间。当构节数目为1~ 5 时对应的机器人工作空间截面,如图4所示。
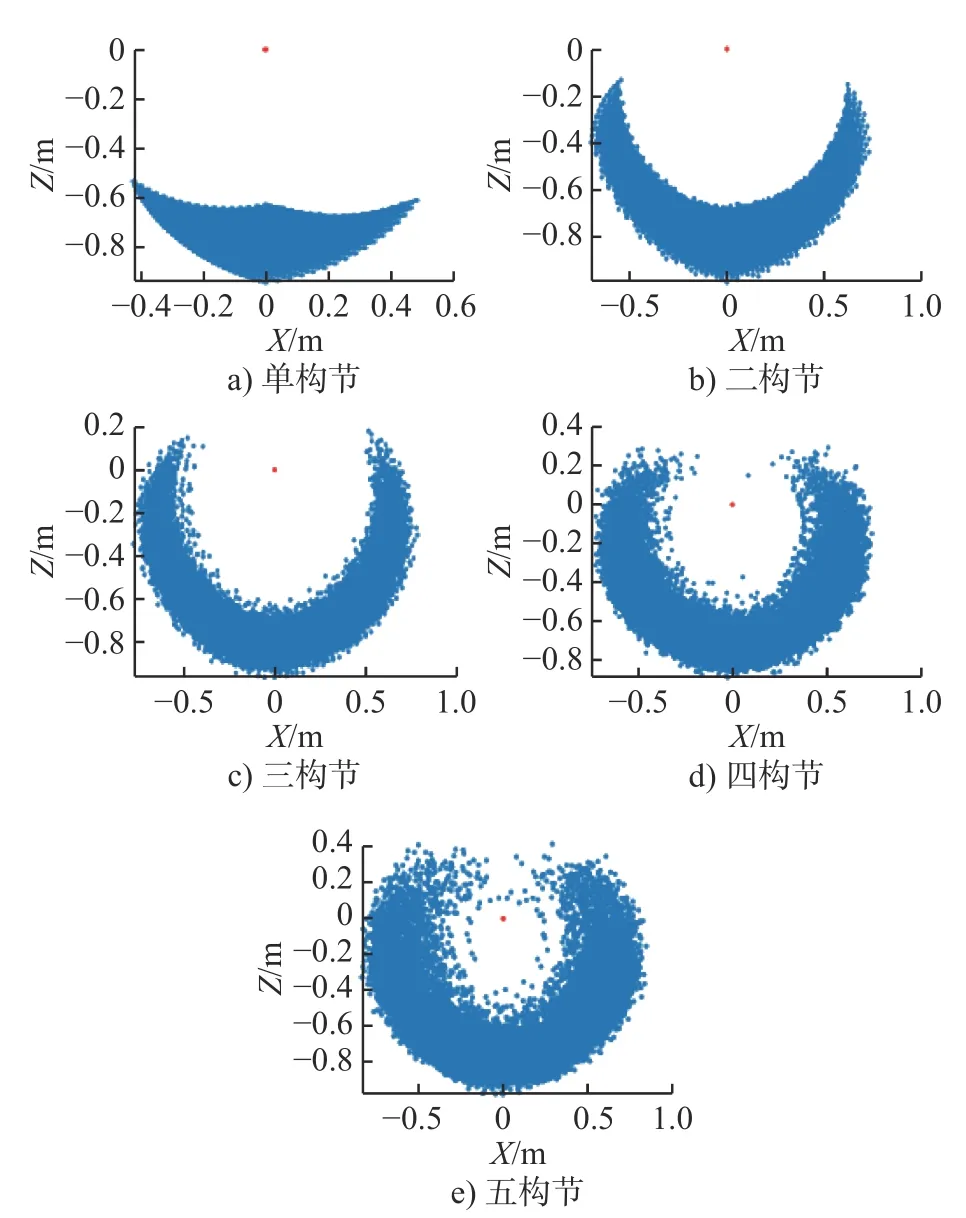
图4 单构节到五构节连续体机器人工作空间截面图
图4 中蓝色点对应工作空间,红色点为坐标原点。连续体机器人工作空间较为特殊,可以看成内外两个曲面之间包裹的区域,少构节的连续体机器人的工作空间更接近伞状,而多构节的连续体机器人工作空间接近于空心球状。当串联的构节数小于3 时,连续体机器人的工作空间较小不能表征出连续体机器人工作空间的基本外形,因此串联构节数必须大于3。
2)奇异位形与灵巧度指标
奇异位形是指,在运动过程中如果机构的运动学、动力学性能瞬间发生突变,机构或处于死点、或失去稳定、或自由度发生变化,使得机构传递运动和力的能力失常。雅克比矩阵的秩可以反映出机器人在关节空间不同位置的奇异性,雅克比矩阵不满秩时意味着机器人到达奇异位形。分析二构节到五构节连续体机器人雅克比矩阵的秩,结果如图5所示。
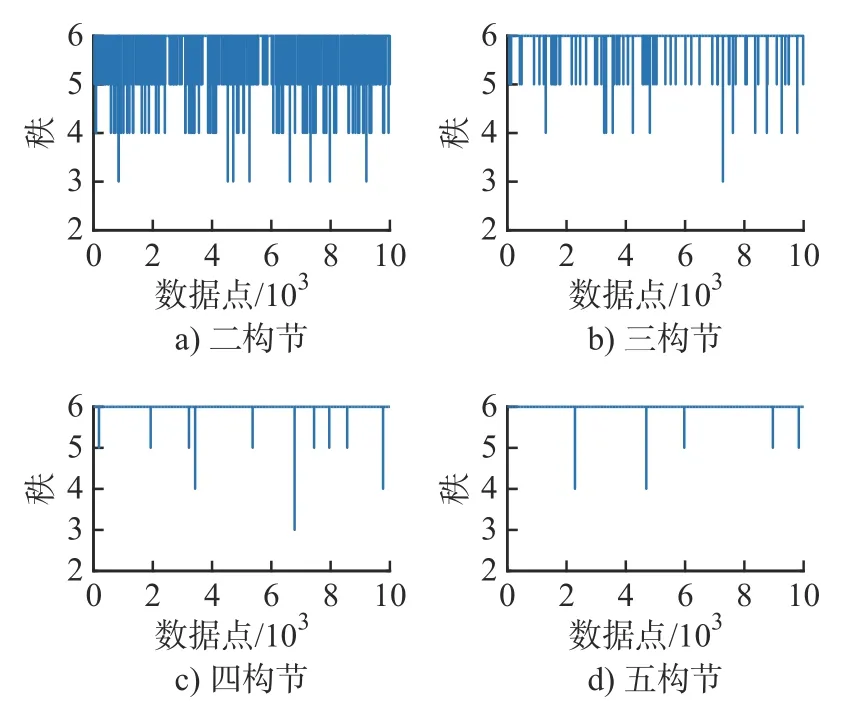
图5 2~ 5 个构节连续体机器人雅克比矩阵的秩
从图5 可以看出,随着连续体机器人构节数目增加,在随机选取的关节空间点中,奇异位形的比例明显降低,尤其是当串联构节数由2 增加到3。这时轨迹规划时避开或远离奇异位形会变得较为容易,机器人的运动性能更好。
3)雅克比矩阵条件数和可操作度
机器人的雅克比矩阵反应了末端执行器达到某一笛卡尔速度需要什么样的关节速度。条件数越大,则雅克比矩阵越病态,机器人在该位形下的灵活性就越差。雅克比条件数和可操作度是两个重要的机器人灵巧度指标。雅克比矩阵条件数可定义为
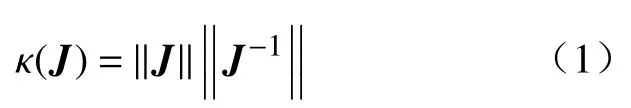
图6 是采用蒙特卡罗方法在关节空间中随机选点计算并统计得到雅克比矩阵条件数。随着构节数目的增加,雅克比矩阵的条件数迅速减小。当构节数目为2 时,条件数大部分都处于106~ 1012之间。当构节数目为3 时,条件数基本都在101~ 103之间。构节数目为4 和5 时,条件数基本在101~102之间。构节数极大地影响了连续体机器人运动学性能,构节越多机器人越灵活。从条件数方面考虑,构节数至少为3。
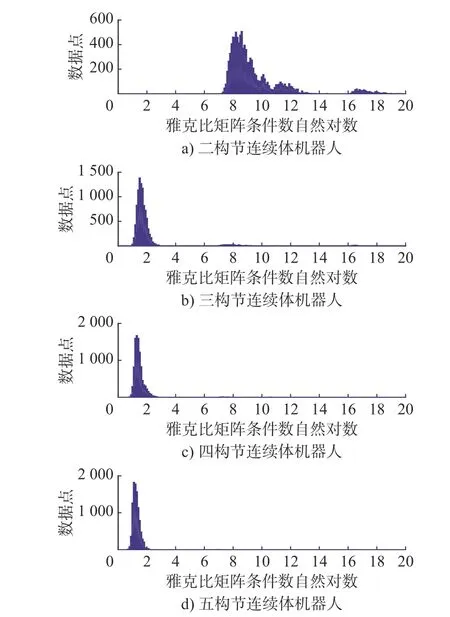
图6 二构节到五构节连续体机器人雅克比矩阵条件数
可操作度ω可定义为
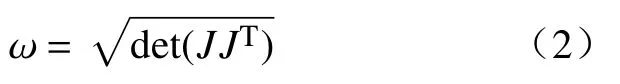
式中:ω越大代表运行性能越好,其最大为1,ω=0 代表机器人处于奇异位形。随着构节的增加,可操作度描述的连续体机器人运动学性能也是大大改善了。图7 为六自由度和八自由度机器人以及三构节连续体机器人的可操作度统计图。
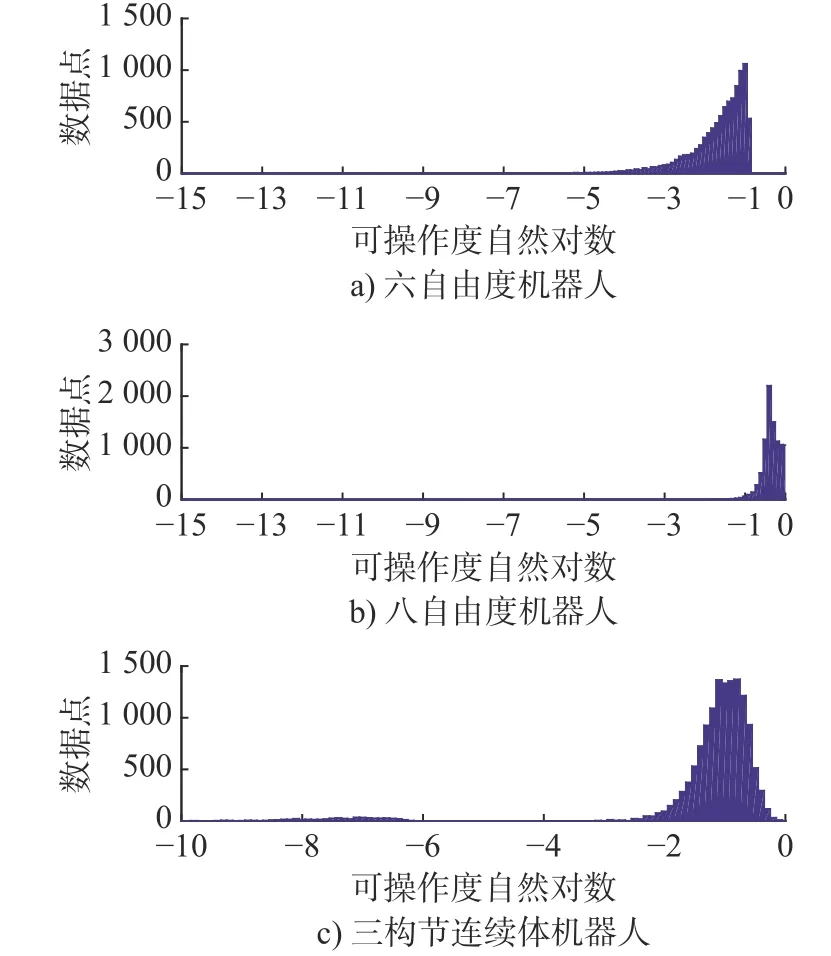
图7 六自由度、八自由度、三构节机器人可操作度
考虑图4~ 图7 的结果:当构节数目为3 时,连续体机器人的工作空间外形已基本能够表征多构节机构的运动空间。在相同数目数据点时,三构节机构的满秩比例已经有很大的提高;构节数大于3 时,机器人条件数减少量已经不明显;三构节的运动性能已经介于六自由度和八自由度机器人之间。为了使仿象鼻机器人结构不过于复杂但又能具备一定的运动性能,确定采用3 个构节串联的形式。
3 仿象鼻气动连续机器人结构参数确定与优选
分析构节模型旨在优化间隔盘数目和构节径向尺寸。采用弹簧—阻尼—质量系统描述气动肌肉(采用力—变形关系描述其刚度,实验测定阻尼为146 N·s/m)。使用Adams/View 模块,建立气动连续体构节的运动模型,单个构节被分为多个小节,节数由间隔盘的数目n确定。
3.1 确定间隔盘数目
间隔盘可以使构节刚度变大,且更加稳定,让其变形接近于常曲率更加利于控制,同时也可增大连续体机构的负载能力。但间隔盘的增加导致整机质量增大,又限制构节的运动性能。研究了空载和在不同负载情况下,间隔盘数对构节最大弯曲角度ψ的影响,其中间隔盘的数目n取值范围为1~ 8。仿真结果如图8 和图9 所示。
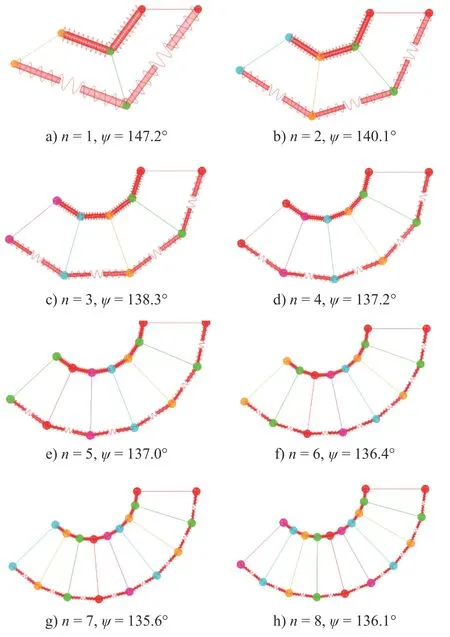
图8 构节在空载下不同间隔盘数目n 时的最大弯曲角度
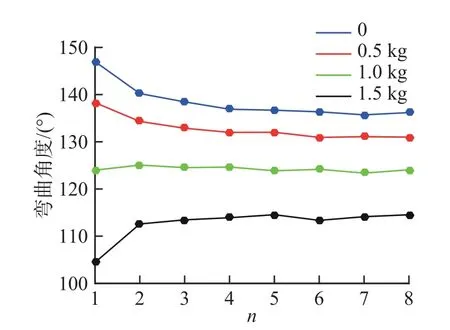
图9 不同负载下弯曲角度与间隔盘数目n 关系曲线
图8 表明,在空载情况下,构节变形量随着间隔盘数目的增加而减小。图9 则说明,当负载小于1.0 kg时,间隔盘越少构节变形越大,而当负载大于1.0 kg,间隔盘越多构节变形越大。间隔盘数目大于4 时,负载能力和变形性能已经基本趋于稳定。因此针对构节的不同负载情况,可以选择不同的间隔盘个数。第一构节的负载最大,第二构节负载次之,第三构节负载最小。结合实际情况,最终确定第一构节、第二构节和第三构节间隔盘数目依次为4 个、3 个和2 个。
3.2 确定构节径向尺寸
定义构节径向尺寸为3 个气动肌肉中心线与端板交点所在圆的半径,即图3 中r表示的尺寸。图10是在间隔盘数为4 时,空载下不同r值对应的构节最大弯曲角度ψ仿真计算结果。由图10 可知,在空载或负载较小时,构节最大弯曲角度随着尺寸r增大而明显减小。
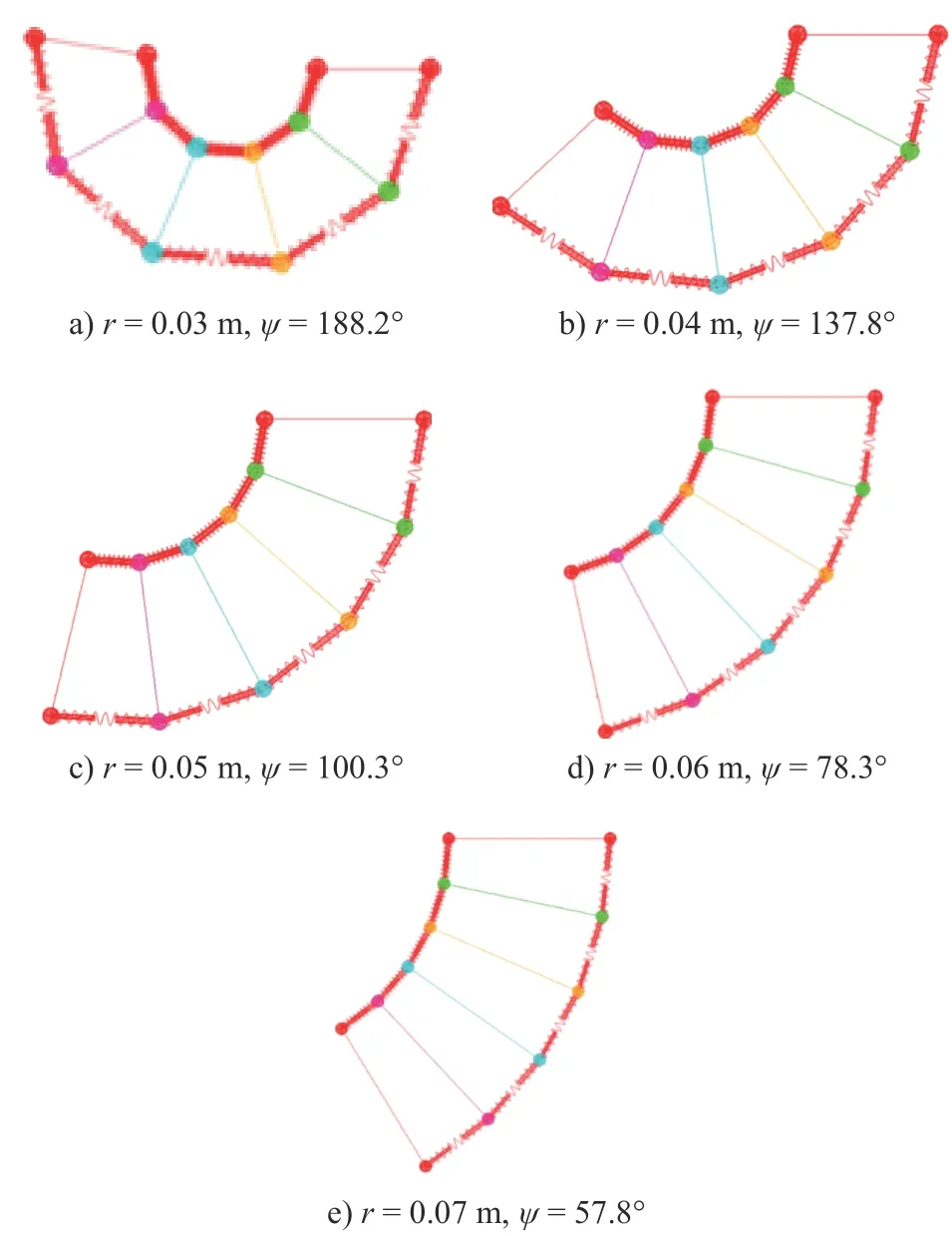
图10 空载时不同r 值下构节的最大弯曲角度值
再考虑负载的情况下,第一构节变形量随r的变化情况,图11 为负载2.0 kg 时变形量随r的变化曲线。
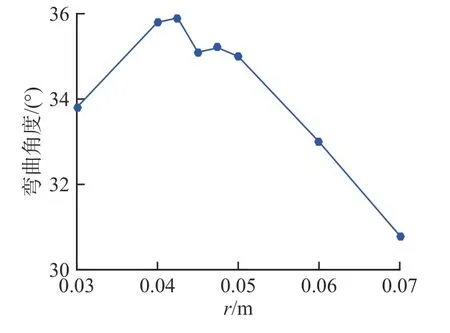
图11 2.0 kg 负载下第一构节最大弯曲角度与r 关系曲线
图11 可以看出第一构节最大弯曲角度随半径r增大先增加后减小,r=0.042 m 对应其峰值。将负载最大的第一构节设为0.042 m,用同样方法分析在略小2.0 kg 负载下第二、三构节弯曲角度和r值关系曲线,取其峰值即r=0.037 m 和r=0.032 m。
4 样机制作与运动实验测试
本机器人的末端执行器设计参照了鱼鳍变形原理[23],其结构简单、重量轻并且强度大,能够自适应所抓物体的外形。在机器人外部安装拉线传感器测量各个气动肌肉长度用以实时反馈机器人各构节变形情况。在初始状态下,机器人机械本体尺寸为760 mm×240 mm×220 mm,其运动部分质量为2.1 kg。制作完成后需要对仿象鼻气动连续体机器人(图12)进行运动性能测试,看是否达到设计目标。
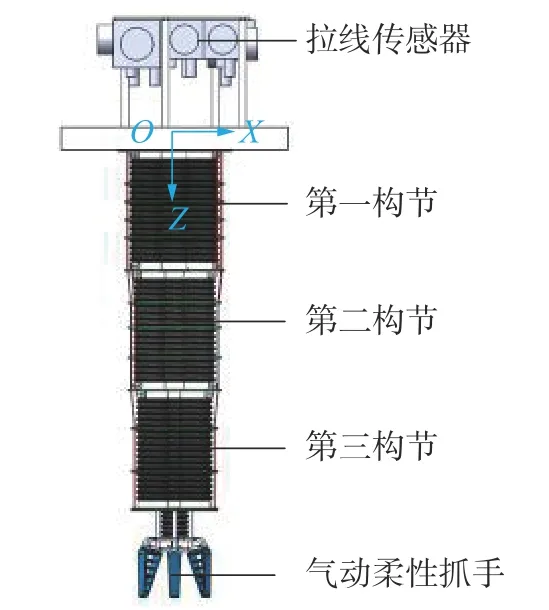
图12 仿象鼻气动连续体机器人结构组成图
机器人9 个气动肌肉的气压是选用电气比例伺服阀(ITV)进行控制。该伺服阀输出气压与输入电信号成比例,内部集成有PID 控制器可对气压进行连续、无级调节,只需控制伺服阀的输入电信号便可使象鼻型机器人实现连续、平滑的运动。
给机器人足够多组的气压值,在MATLAB 中拟合测试得到的数据,可以确定机器人在XZ平面内的工作空间,截面图如图13 所示。工作空间大体形状与仿真分析基本一致,主要区别体现在左右两侧的对称性。由于仿象鼻气动连续体机器人构节结构的特点,机器人工作空间是旋转对称而非中心对称的。把机器人的工作空间绕其中轴线旋转120°的整数倍得到的三维空间才会与原工作空间重合。
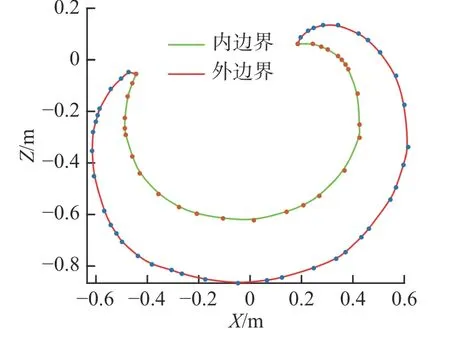
图13 XZ 平面内机器人实际工作空间截面图
给9 个气动肌肉和1 个执行器分别通入图14a)所示随时间变化的气压,机器人便可完成图14b)所示的运动与动作。
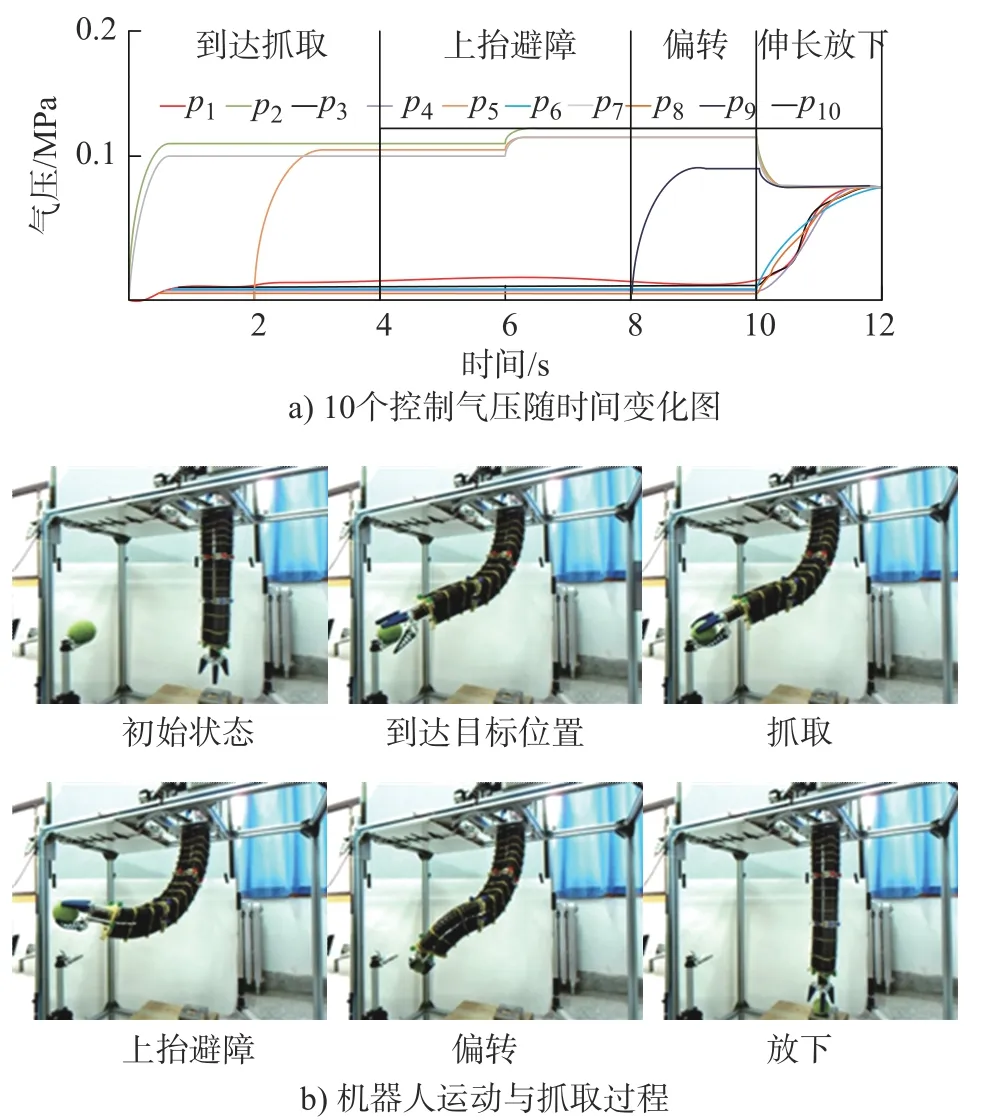
图14 仿象鼻气动连续体机器人运动与抓取过程
图14 展示了机器人伸长、弯曲和偏转运动;可完成设定位置网球的抓取和放下动作;运动状态可由拉线传感器反馈给计算机,用于形成闭环控制。这说明所设计的仿象鼻连续体机器人实现了1.1 节中提到的3 个设计目标。给气动肌肉通入最大工作气压(0.14 MPa),便可得到此时的拉线长度,代入到常曲率运动学模型中便可得到机器人基本变形能力与运动范围,如表3 所示。
表3 中第一构节的最大弯曲角度为62.7°,受负载、间隔盘数量、构节半径等因素影响,二、三构节最大弯曲角度逐渐增大,这些都验证了仿真结果准确性。采用视觉反馈对机器人末端重复定位精度进行测试,在工作空间外边界偏下的位置,机器人末端重复定位误差较大,在工作空间越靠近上边缘的位置,此时各个构节越接近弯曲变形极限,机器人的末端定位精度越高,误差约为1 cm。误差来源主要是气动肌肉材料特性带来的误差即控制气压完全相同的情况下,因柔性材料的迟滞性,每一次气动肌肉的变形量并不都相同。
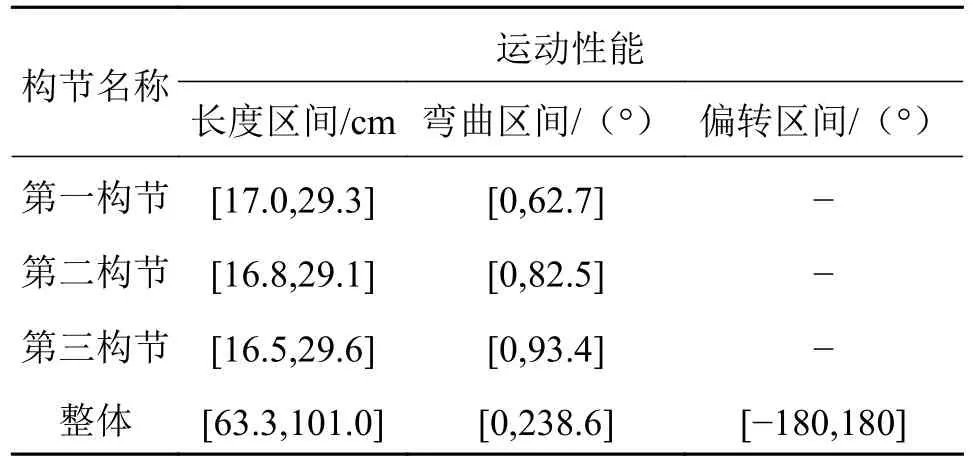
表3 仿象鼻气动连续体机器人空载变形能力与运动范围表
5 结论
针对仿象鼻气动连续体机器人,结合象鼻仿生运动要求,提出了多构节串联的设计方案。再从工作空间、灵巧度和可操作度等方面分析了构节数对机器人设计的影响,最终确定设计3 构节串联仿象鼻气动连续体机器人。这样即可使机器人具备较大的工作空间与较好的运动性能,又不会使控制系统过于复杂。利用Adams 对构节进行仿真的结果表明,构节的间隔盘数量和径向尺寸对其负载能力和变形能力影响较大,设计时各构节需分别考虑以确定最优参数。对样机的测试结果表明,机器人可以完成伸长、弯曲、偏转和给定物体的抓取与搬运工作,实现3 个设计目标。
