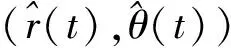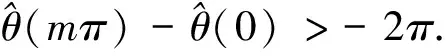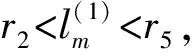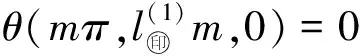一类单侧有界不对称Duffing方程的对称周期解
2022-05-13成红胜
成 诚, 成红胜
(1. 江苏师范大学 数学与统计学院, 江苏 徐州 221116; 2. 盐城师范学院 信息工程学院, 江苏 盐城 224001)
考虑二阶Duffing方程
x″+g(x)=p(t)
(1)
的2π-周期解的存在性和多解性问题,其中p:R→R是2π-周期的连续偶函数,g:R→R是局部Lipschitz连续函数,g(0)=0,满足
(g1) ∃d0>0使得对x≥d0都有
g(x)>2p0,
其中p0:=max{|p(t)|:t∈[0,2π]};
(g2) ∃M0>0,∀s∈R+,|g(s)|≤M0;
(g3) 存在正数0 由于二阶Duffing方程(1)与许多实际问题相关联[1-2],因而广受关注.其中,关于方程周期解的存在性和多解性问题已有许多研究工作.例如,在超线性条件 (2) 下,丁伟岳[3]运用自己证明的推广Poincare-Birkhoff扭转不动点定理证明了方程(1)无穷多个调和解和次调和解的存在性.Ding等[4]在更一般性的超线性条件 (τ0) 下推广了文献[4]的结论,其中 为自治方程x″+g(x)=0的周期轨道 在文献[10]中,在条件(2)和假设p(t)是偶周期函数的条件下,Nakajima证明了无穷多个偶的调和解和次调和解的存在性,并且在g(x)是C1函数的假设下证明了偶的次调和解的稠密性分布结果.对于对称周期解的研究,针对非线性Hill方程也有一些结果,参见文献[11-12].在上述有关二阶方程的对称周期解的研究中没有关于不对称方程的讨论,一个有趣的问题是:文献[10-12]的结论能否推广到一些不对称方程的情形. 本文讨论一类不对称Duffing方程的对称周期解问题.所谓不对称方程是指当x<0和x>0时,回复力g(x)满足不同的非线性条件.在本文中,在一侧回复力是有界函数且另一侧回复力满足半线性条件时,证明方程(1)有无穷多个偶次调和解.同时,偶次调和解是稠密性分布的.由于偶函数是对称函数,因此偶的周期解亦称为对称周期解.本文首先运用相平面分析的方法对等价系统解的动力行为进行分析,得到在充分大的区域外系统解的动力行为.之后利用解的性质在相平面上构造适当大的圆环,使得Poincaré映射在环的边界具有扭转性,再利用偶周期解存在的充分必要条件证明了方程(1)无穷多个偶的次调和解的存在性和稠密性分布结果. 令x′=y,则可得与方程(1)等价的系统 (2) 类似于文献[11]中的做法,构造辅助系统 (3) 其中连续函数η:R2→R称为截断函数,满足 且|η(a,b)|≤1.易见,如果方程(3)的解(x(t),y(t))在区间I⊂R上满足|(x(t),y(t))|≥1,则(x(t),y(t))也是系统(2)定义在区间I上的解. 下面,记(x(t;x0,y0),y(t;x0,y0))是方程(3)在t=0时刻以(x0,y0)为初值条件的解.易证 引理 1.1方程(3)的解(x(t;x0,y0),y(t;x0,y0))是唯一且全局存在的. 从而,由引理1.1有: 推论 1.1对任给的正实数T>0和H>0都存在一个正数R0:=R0(T,H)>0,对任意的(x0,y0)∈R2,只要|(x0,y0)|≥R0,则(2)式的解(x(t;x0,y0),y(t;x0,y0))一定满足 |(x(t;x0,y0),y(t;x0,y0))|>H, ∀t∈[-T,T]. 注 1.1由推论1.1,易见,对任意的T>0,存在正数M:=M(T)>0使得对方程(3)的任意解(x(t),y(t)),只要|(x(t),y(t))|≥M,则 |(x(t),y(t))|≥1,t∈[-T,T]. 从而,(x(t),y(t))也是系统(2)定义在[-T,T]上的解. 因为g(0)=0,故(0,0)是方程(3)的平衡点,从而由解的存在唯一性定理,方程(3)的任意非零解在任何有限时间内不会通过原点.对方程(3)初值不为(0,0)的解,可以定义它的极坐标形式 其中r(t)和θ(t)是关于t的C1函数.显然,∀t∈R,r(t)、θ(t)满足 记(r(t;t0,r0,θ0),θ(t;t0,r0,θ0))为方程(4)的满足初始条件r(t0)=r0和θ(t0)=θ0的解. 引理 1.2∃R1>1,对(2)式的任意解(x(t),y(t)),只要r(t)>R1就有 θ′(t)<0. 证明当(x(t),y(t))∈Ⅰ时,易见-sin2θ(t)≤-sin2δ.由(4)式知存在M1>0,当r>M1时有 其中,p0:=max{|p(t)|:t∈[0,2π]}.从而有 θ′(t)≤-sin2δ<0. 类似可证:存在M2>0,使得当(x(t),y(t))∈Ⅲ且r(t)>M2时有θ′(t)<0. 当(x(t),y(t))∈Ⅱ时,cos(取δ充分小).因此,在Ⅱ内,当r→+∞时有x→+∞.从而,由(g1),对充分大的正数M3>0,当r(t)>M3时(注意到有 从而由(4)式知θ′(t)<0. 当(x(t),y(t))∈Ⅳ时,首先,-sin2θ(t)≤-sin2δ.其次,由(g3)知,存在d1>0,当x≤-d1时有g(x)<0.取M4>0充分大使得当(x(t),y(t))∈Ⅳ且r(t)>M4时,如果-d1 (x(t),y(t))∈Ⅳ 且r(t)>M4时有 类似可证:存在M5>0,使得当(x(t),y(t))∈Ⅵ且r(t)>M5时有θ′(t)<0. 当(x(t),y(t))∈Ⅴ时,由(g3),取M6>0适当大使得当r(t)>M6时x(t)<-d1且g(x)<-2p0.从而,θ′(t)<0. 取R1>max{Mi:i=1,2,…,6},则(1)和(2)式成立.证毕. 引理1.2指出,在充分大的圆盘外,系统(3)的解在总是绕着原点作顺时针旋转. 引理 1.3设τ(R)为方程(3)的解在区域{(x,y):|(x,y)|≥R}内转一圈所用时间的下确界,则 证明对充分大的R>R1,只需计算解在 1.4.2 搭建成本分析。对2015年建造避雨棚时所用的搭建成本进行统计,包括用工、肥料、避雨棚膜、架材、苗木等。 {(x,y):|(x,y)|≥R} 内通过区域 Ω:={(x,y):-x 所需时间即可. θ′(t)=-cos2θ(t)+ 因此,轨线穿过Ω所需的时间τ满足 θ(t1)-θ(t0)<-4π. 证明首先,在XOY右半平面上定义一些区域.记 Ⅰ={(x,y):0≤x Ⅱ={(x,y):x≥d0,y≥d0}, Ⅲ={(x,y):x≥d0,-d0 Ⅳ={(x,y):x≥d0,y≤-d0}, Ⅴ={(x,y):0 其中d0在(g1)中给出. 设(x(t),y(t))是方程(3)的定义在[τ,τ+T]上的解,满足 r(t)>2max ∀t∈[τ,τ+T], 其中τ∈R是任意的一个实数,T>0是一个正实数,M1:=M0+p0,其中M0、p0在(g2)、(g1)中定义.下面将在各个区域讨论r(t)的变化情况. (i) 设∀t∈I1⊂[τ,τ+T],有(x(t),y(t))∈Ⅰ.因为 所以∀t,s∈I1,有 |y(t)-y(s)|≤2M1. 从而, 所以 易见F1(r),F-1(r):R→R都是单调递增的函数.在区域Ⅴ中有类似的讨论,并且存在单调递增的函数 (ii) 设∀t∈I2⊂[τ,τ+T],有 (x(t),y(t))∈Ⅱ. 由(2)式得 ydy=(-g(x)+p(t))dx. 设t0,t1∈I2,t0 (5) 从而有 其中t=t(x)是x=x(t)的反函数且ξ∈[x0,x1],则有 或 因为y0 从而 (9) 因此 (10) 同时,注意到d0≤x0 (11) 从而 (12) 则易见,F-2和F2都是单调递增函数且 F-2(r0) (13) 在区域Ⅵ中有类似的讨论,并且存在单调递增的函数 F±6(r):=F±2(r). (iii) 设∀t∈I3⊂[τ,τ+T],有 (x(t),y(t))∈Ⅲ. ∀t0,t1∈I3,因为 d0(t1-t0) 则 |r(t1)-r(t0)|≤ (14) 从而 (15) 易见,F-3和F3都是单调递增函数.在区域Ⅶ中有类似的讨论,并且存在单调递增的函数 F±7(r)=F±3(r). (iv) 类似于(ii)中的讨论,若 ∀t∈I4⊂[τ,τ+L], 有 (x(t),y(t))∈Ⅳ, 则可以找到2个单调递增的函数F±4(r)使得对任意的t0,t1∈I4,t0 F-4(r(t0))≤r(t1)≤F4(r(t0)). (16) 接下来,在XOY左半平面上定义一些区域.由(g3)知,存在d1>0,使得当x≤-d1时有 g(x)<-(L0+1)p0. 记 Ⅵ={(x,y):-d1 Ⅶ={(x,y):x≤-d1,y≤-d1}, Ⅷ={(x,y):x≤-d1,-d1 Ⅸ={(x,y):x≤-d1,y≥d1}, Ⅹ={(x,y):-d1≤x<0,y≥d1}. (v) 类似于(i)中的讨论,若∀t∈I6⊂[τ,τ+T],有(x(t),y(t))∈Ⅵ,则可以找到2个单调递增的函数F±6(r)使得对任意的t0,t1∈I6,t0 F-6(r) (17) 同样地,若∀t∈I10⊂[τ,τ+L],有(x(t),y(t))∈Ⅹ,则可以找到2个单调递增的函数F±10(r)使得对任意的t0,t1∈I10,t0 F-10(r(t0))≤r(t1)≤F10(r(t0)). (18) (vi) 类似于(iii)中的讨论,若∀t∈I8⊂[τ,τ+L],有(x(t),y(t))∈Ⅷ,则可以找到2个单调递增的函数F±8(r)使得对任意的t0,t1∈I8,t0 F-8(r(t0))≤r(t1)≤F8(r(t0)). (19) (vii) 设∀t∈I7⊂[τ,τ+T],有 (x(t),y(t))∈Ⅶ. 由(g3)和(4)式知,只要取d1充分大,就有 |r′(t)|≤(L0+1)r, 从而对任意的t0,t1∈I7,t0 r(t0)e-(L0+1)T≤r(t1)≤r(t0)e(L0+1)T. (20) 取F-7(r):=re-(L0+1)T及F7(r):=re(L0+1)T,则F±7(r)是2个单调递增的函数. 类似地,可定义2个单调递增的函数F±9(r)使得若∀t∈I9⊂[τ,τ+L]有(x(t),y(t))∈Ⅷ,则对任意的t0,t1∈I9,t0 F-9(r(t0))≤r(t1)≤F9(r(t0)). (21) 这样,在区域Ⅰ,Ⅱ,…,Ⅹ上分别定义了20个单调递增的函数F±1,F±2,…,F±10定义 γ1(r):=F1∘F2∘…∘F10∘ F1∘F2∘…∘F10(r), 且 γ-1(r):=F-1∘F-2∘…∘F-10∘ F-1∘F-2∘…∘F-10(r). 这样,无论初始点在哪一个区域,对于充分大的C>0有∀r>C,对∀t1,t2∈[τ,τ+L]且t1 θ(t2)-θ(t1)<-2π. 类似地,只要r(t1)≥r且r(t2)≤γ-1(r),就有 θ(t2)-θ(t1)<-2π. 显然,γ1(r)和γ-1(r)是单调递增函数.令 γ(r):=γ1∘γ1(r), γ(-1)(r):=γ-1∘γ-1(r), 则γ、γ(-1)即为所求. 若x(t)为(1)的偶周期解,则称初值点(x(0),x′(0))为一个ε-点.由于x(t)是偶函数,所以必有x′(0)=0.若一个偶周期解x(t)的最小周期为2mπ(m∈Z+),则称ε-点(x(0),x′(0))为m阶的. 在下面,对任一个t0∈R和(r0,θ0)∈R+×R,r0>0,设(r(t;t0,r0,θ0),θ(t;t0,r0,θ0))是方程(4)的满足初始条件 r(t0)=r0,θ′(t0)=θ0 的解.特别地,若t0=0,记 (r(t;r0,θ0),θ(t;r0,θ0))= (r(t;0,r0,θ0),θ(t;0,r0,θ0)). 相应地,记(x(t;x0,y0),y(t;x0,y0))为方程(2)的满足(x(0),y(0))=(x0,y0)的解. 下述引理见文献[13]. 引理 2.1方程(1)的解x(t)是一个偶周期解当且仅当存在一个正整数m,使得 x′(0)=x′(mπ)=0. 特别地,ε-点(x(0),x′(0))是m阶的当且仅当x′(kπ)≠0,k=1,2,…,m-1. 定理 2.1假设(g1)~(g3),则存在m1∈Z+,对∀m≥m1,系统(1)至少存在2个最小正周期为2mπ的偶周期解. 证明取r1>max易见r3>r2>r1.记闭圆环 B(r2):={(x,y):r1≤|(x,y)|≤r3}. 由引理1.2,在B(r2)内有 θ′(t)<0, ∀t∈R. 因此,由(4)式、θ′的连续性和系统的周期性,存在正数b>0,在闭圆环{(x,y):r1≤|(x,y)|≤r3}内有 θ′≤-b, ∀t∈R. 可以证明,对上述的a,取 则对任给的θ0∈R及T≥T0,方程(4)的以(r2,θ0)为初值解 (r(t),θ(t)):=(r(t;0,r2,θ0),θ(t;0,r2,θ0)) 满足 θ(T)-θ0<-2π. (22) 令m1为充分大的正整数且满足 m1π≥T0, 则对任意固定的整数m≥m1以及方程(4)的满足初始条件r(0)=r2的任一解(r(t),θ(t)),都有 θ(mπ)-θ(0)<-2π. r(t)≥r4, 0≤t≤mπ, 则有 θ(mπ)-θ(0)>-2π. 特别地 θ(mπ;r2,ϑ0)-θ(0;r2,ϑ0)<-2π 和 θ(mπ;r5,ϑ0)-θ(0;r5,ϑ0)>-2π, 其中ϑ0≡0(modπ). 从而 下面,任取方程(1)的2个ε点p1、p2,其中 p1=(c1,0),p2=(c2,0),c1 主要结果是: 类似于文献[10]中定理3的证明,有1 预备引理
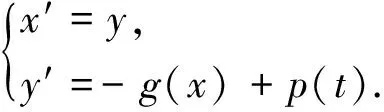
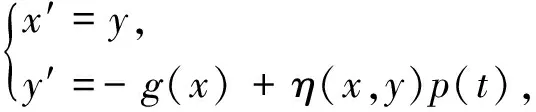
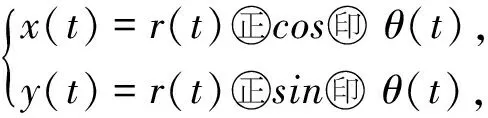
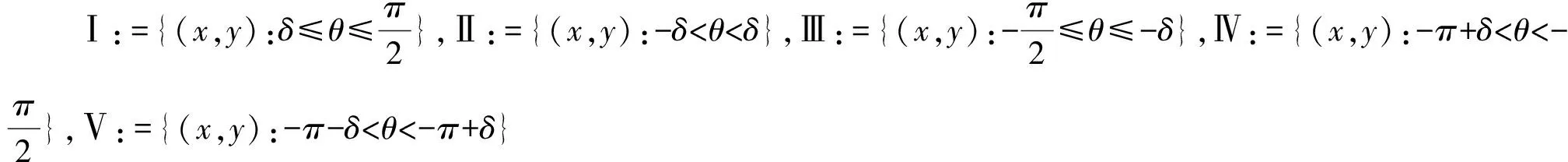
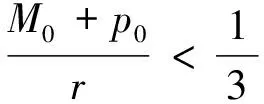
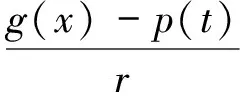

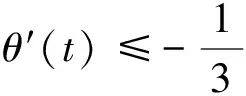
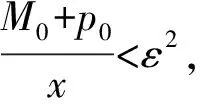


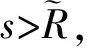
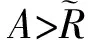
2 主要结论