受非线性白噪声驱动的随机非自治不可压缩非牛顿流体的弱拉回吸引子

晏 涛, 邹爱红, 张 露, 舒 级*

(1. 四川师范大学 数学科学学院, 四川 成都 610066; 2. 四川师范大学 可视化计算与虚拟现实四川省重点实验室, 四川 成都 610066)

假设O是R2上的光滑区域,考虑在具有非线性扩散项的白噪声驱动下的随机非自治不可压缩非牛顿流体：

x=(x1,x2);

▽·u=0,u|∂O=0,

(1)

其中未知向量函数u=u(x,t)=(u(1),u(2))表示流体的速度,

g(x,t)=g(t)=(g(1),g(2))

τ

eij=e

(2)

其中μ0、μ1、α、ε1依赖于温度和压力的参数,本文μ0、μ1、α、ε1是正常数且0<α<1,在(2)式中如果τij(e(u))和eij(u)是线性关系,就称相应的流体是牛顿流体.一般来说,气体、水、机油、醇和简单的碳氢化合物往往是牛顿流体,它们的运动可以用Navier-Stokes方程来描述.如果τij(e(u))和eij(u)是非线性关系,那么这个流体就叫做非牛顿流体.例如,熔融的塑料、聚合物溶液和涂料往往是非牛顿流体.由于速度的梯度|▽u|相对较大,方程(1)可以看成是“修正的”随机Navier-Stokes方程.显然,当α=μ1=0,(1)式退化为随机Navier-Stokes方程,而当μ1=μ0=0时退化为随机欧拉方程;它们都是牛顿流体.注意到,(1)式中的随机项在It积分下是有意义的.

本文将在适当的Bochner空间中研究方程(1)弱拉回均方随机吸引子的存在唯一性,这种弱拉回均方随机吸引子不同于逐点拉回随机吸引子.随机动力系统的逐点拉回随机吸引子的概念首先在文献[1-3]中提出,随后许多专家也进行了广泛的研究;自治的随机方程可以参考文献[4-24],非自治的随机方程可以参考[25-29].特别地,随机方程(1)的逐点拉回随机吸引子的存在唯一性可以在文献[2,6,14]中查阅,但是这些论文对扩散项σ施加了非常严格的条件,要求σ(t,u)在u中是线性的,或者具有非常特殊的结构,比如反对称.据作者所知,当σ是一般的Lipschitz非线性函数时,目前还没有关于逐点拉回随机吸引子存在的结果.

为了研究同时具有非线性漂移和非线性噪声的随机反应扩散方程的渐近行为,Wang[30]引入了弱拉回均方随机吸引子,并在文献[31]中进一步研究.之后,Wang[32]讨论了具有一般Lipschitz非线性扩散项的随机非自治Navier-Stokes方程的弱拉回均方随机吸引子的存在性.本文在σ(t,u)是Lipschitz非线性函数的条件下,证明了随机非自治不可压缩非牛顿流体方程(1)的弱拉回均方随机吸引子的存在唯一性(见定理2.2).这似乎是关于具有一般Lipschitz非线性扩散项的随机非自治不可压缩非牛顿流体方程的弱拉回均方随机吸引子存在性的第一个结果.

下文首先在适当的Bochner空间中定义了带Lipschitz非线性扩散项的随机非自治不可压缩非牛顿流体方程(1)的均方随机动力系统,然后构造了(1)式的一个弱紧拉回吸收集,并证明了弱拉回均方随机吸引子的存在唯一性.

1 预备知识

本节在滤子概率空间中给出了非自治随机不可压缩非牛顿流体(1)的解的存在性,并定义了一个均方随机动力系统.为此,需要将问题(1)重新表述为抽象的随机微分方程,本文使用了以下符号：

Lp(O)-2维勒贝格空间并定义了范数‖·‖Lp(O);特别地,‖·‖L2(O)=‖·‖;

Hm(O)-2维索伯列夫空间{φ=(φ1,φ2)∈L2(O),▽kφ∈L2(O),k≤m}并有范数‖·‖Hm(O),其中k、m是非负的整数;

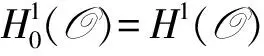
H=L2(O)中V的闭包并有范数‖·‖;H′=H的对偶空间;

V=H2(O)中V的闭包并有范数‖·‖V;V′=V的对偶空间,(·,·)为H中的内积,〈·,·〉为V和V′的对偶内积.

进一步引入一些算子.令

(3)

由文献[33],有以下引理.

引理 1.1存在2个正常数c1和c2它们仅依赖于O且有

从a(·,·)的定义和引理1.1可得a(·,·)在V上定义了一种正定对称双线性形式.作为Lax-Milgram引理的推论,得到了一个等距算子A∈Γ(V,V′),并有

〈Au,v〉=a(u,v), ∀u,v∈V.

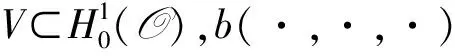
b(u,v,w)=-b(u,w,v),

b(u,v,v)=0, ∀u,v,w∈V.

(5)

对任意的u∈V有

〈B(u),w〉=b(u,u,w), ∀w∈V,

(6)

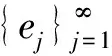
Qej=qjej, ∀j∈N,qj≥0.

W是一个定义在(Ω,F,{Ft}t∈R,P)上的Q维纳过程并在H上取值,从文献[34]中可得

W(t)=在L2(Ω,F,H),

W

其中S*是S的伴随算子.

最后,由u∈V,设

定义N(u)

∀v∈V.

那么函数N(u)从V到V′是连续的.当u∈D(A)时,N(u)能通过

∀v∈H

(7)

延拓到H.从物理角度看,(1)和(2)式的初边值问题可表示为:

(8)

▽·u=0,x∈O,

(9)

u=0,τijlnjnl=0,x∈∂O,

(10)

u|t=τ=u0,

(11)

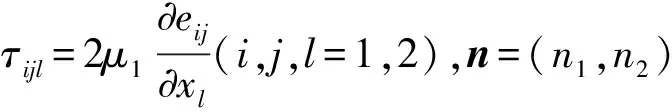
除去p,问题(8)～(10)在螺线向量场中的弱形式可以表示如下

(12)

且有初值

u(τ)=u0,

(13)

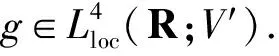
在本文中,假设σ:R×V→L2(H0,H)是满足以下条件的连续映射：存在非负常数β1,β2,…,β5使得对所有的t∈R和u,v∈V,有

(14)

(15)

现在给出(12)～(13)式解的存在性.

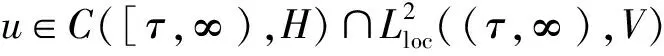
依概率几乎处处成立.

在(14)和(15)式的条件下,(12)和(13)式的解的存在唯一性可参考文献[34].

命题 1.3假设(14)和(15)式成立，则存在ε0>0使得对每一个ε∈(0,ε0),τ∈R和u0∈L4(Ω,Fτ;H),问题(12)和(13)有唯一解u∈L4(Ω,C([τ,τ+T],H))∩L2(Ω,L2((τ,τ+T),V)),对每一个T>0,并有

E(

‖u(s)‖2)ds)≤M1(1+E(‖u0‖4)), (16)

其中M1>0是一个不依赖于u0的常数.

因为u∈C([τ,∞),H)依概率处处成立,由(16)式和勒贝格控制收敛定理可得u∈C([τ,∞),L4(Ω,F;H)),因此(12)和(13)式能定义一个均方随机动力系统.给定t∈R+和τ∈R,设Φ(t,τ)是从L4(Ω,Fτ;H)到L4(Ω,Fτ+T;H)的一个映射且有

Φ(t,τ)(u0)=u(t+τ,τ,u0),

其中u0∈L4(Ω,Fτ;H),u是(12)和(13)系统的具有初值u0的解.通过解的唯一性,可知对每一个t,s≥0和τ∈R,有

Φ(t+s,τ)=Φ(t,s+τ)∘Φ(s,τ).

因此,Φ是文献[32]中定义1.1下的在(Ω,F,{Ft}t∈R,P)上L4(Ω,F;H)中的均方随机动力系统.

回顾在O上的庞加莱不等式:存在一个正常数λ使得

(17)

令B={B(τ)⊆L4(Ω,Fτ;H):τ∈R}是一个非空有界集族使得

(18)

其中

‖B(τ)‖L4(Ω,Fτ;H)=

记D为具有性质(18)的所有非空有界集族的集合:

D={B={B(τ)⊆L4(Ω,Fτ;H):

B(τ)≠0,τ∈R}},

(19)

其中B(τ)有界且B满足(18)式.

为了证明Φ的弱D拉回均方随机吸引子,假设确定的外力项g满足

显然(20)式不需要当s→±∞时g(s)在V′中有界.作为(20)式的一个推论,有

2 非自治不可压缩非牛顿流体的弱D拉回均方随机吸引子

本节证明问题(12)和(13)在(Ω,F,{Ft}t∈R,P)上L4(Ω,F;H)中弱D拉回均方随机吸引子的存在唯一性.先对解进行一致估计,然后为系统构造了一个D拉回弱紧吸收集.

引理 2.1假设(14)和(15)式成立,则存在ε0>0使得对每一个0<ε≤ε0，每一个τ∈R和B={B(t)}t∈R∈D,并存在T=T(τ,B)>0使得对所有t≥T,问题(12)和(13)的解u满足

E(‖u(τ,τ-t,u0)‖4)≤

M2+M2e

其中u0∈B(τ-t),M2是不依赖于τ和B的正常数.

证明从形式上推导出期望的一致估计,但是所有的计算都可以通过像Galerkin方法这样的极限过程来验证.首先,根据It公式和(12)式得到

d(‖u(r)‖2)=2ε(u(r),σ(r,u(r)))dW+

(-4μ1a(u,u)-2〈u(r),N(u〉)+

2〈u(r),g(r)〉+

(21)

d(‖u(r)‖4)=4ε‖u(r)‖2×

(u(r),σ(r,u(r)))dW+

2‖u(r)‖2(-4μ1a(u,u)-

2〈u(r),N(u)〉+2〈u(r),g(r)〉+

(22)

其中σ*是σ的伴随算子.对(22)式取期望,对r≥τ-t,有

8μ1E(‖u(r,τ-t,u0)‖2a(u,u))+

4E(‖u(r,τ-t,u0)‖2〈u(r,τ-t,u0),N(u)〉)=

4E(‖u(r,τ-t,u0)‖2〈u(r,τ-t,u0),g(r)〉)+

2ε2E(‖u(r,τ-t,u0)‖2

4ε2E(‖σ*(r,u(r,τ-t,u0))×

(23)

现在对(23)式右边的每一项进行估计.首先,有

4‖u(r,τ-t,u0)‖2|〈u(r,τ-t,u0),g(r)〉|≤

4‖g(r)‖V′‖u(r,τ-t,u0)‖2×

‖u(r,τ-t,u0)‖V≤

μ1c1λ‖u(r,τ-t,u0)‖4+

(24)

2ε2‖u(r,τ-t,u0)‖2×

2ε2(β1‖u(r,τ-t,u0)‖2+

β2‖u(r,τ-t,u0)‖4+

(25)

对(23)式右边的最后一项,有

‖u(r,τ-t,u0)‖2≤

‖u(r,τ-t,u0)‖2≤

‖u(r,τ-t,u0)‖2,

根据(25)式,对所有0<ε≤ε0,有

(26)

现在对(23)式左边每一项进行估计.

8μ1‖u(r,τ-t,u0)‖2a(u,u)≥

8μ1c1‖u(r,τ-t,u0)‖2×

(27)

由文献[33],〈u(r,τ-t,u0),N(u)〉是非负的,所以有

4‖u(r,τ-t,u0)‖2×

〈u(r,τ-t,u0),N(u)〉≥0.

(28)

由(23)～(28)式,对0<ε≤ε0和r≥t-τ有

4μ1c1E(‖u(r,τ-t,u0)‖2

3μ1c1λE(‖u(r,τ-t,u0)‖4)+

(29)

因此,由(17)式对0<ε≤ε0和r≥t-τ,则

μ1c1λ‖u(r,τ-t,u0)‖4≤

(30)

利用Gronwall引理,由(30)式可以得到

E(‖u(r,τ-t,u0)‖4)≤e-μ1c1λtE(‖u0‖4)+

(31)

因为u0∈B(τ-t)和B∈D,当t→0时,

e-μ1c1λtE(‖u0‖4)=

e-μ1c1λτe-μ1c1λ(τ-t)E(‖u0‖4)≤

e-μ1c1λτe-μ1c1λ(τ-t)‖B(τ-t)‖L4(Ω,Fτ-t;H)→0.

因此,存在T=T(τ,B)>0使得

e-μ1c1λtE(‖u0‖4)<0

对所有t≥T,结合(31)式从而完成证明.

现在准备证明Φ的弱D拉回均方随机吸引子的存在性.

定理 2.2假设(14)和(15)式成立,则存在ε0>0使得对每一个0<ε≤ε0,问题(12)和(13)式的均方随机动力系统Φ在(Ω,F,{Ft}t∈R,P)上L4(Ω,F;H)中有唯一的弱D拉回均方随机吸引子A={A(τ):τ∈R}∈D.

证明给定τ∈R,记

K(τ)={u∈L4(Ω,F;H):

E(‖u‖4)≤R(τ)},

其中

R(τ)=M2+M2e

M2是引理2.1中相同的正常数.因为K(τ)是自反Banach空间L4(Ω,F;H)中的有界闭凸子集,可得K(τ)在L4(Ω,F;H)中是弱紧的.因此,由(20)式可以得到

又因为K={K(τ):τ∈R}∈D,结合引理2.1可知K是Φ的弱紧D拉回吸收集.于是Φ的弱D拉回均方随机吸引子A∈D的存在唯一性可以由文献[32]中命题2.5得到.作为特例,根据引理2.1的证明,如果(14)式中的常数β1是0,并对所有的x∈O和t∈R,外力项g(x,t)=0,那么随机方程(1)对于ε来说是指数稳定的,即所有解在L4(Ω,F;H)中以指数率都拉回收敛到零,具体地说,有以下结果.

定理 2.3假设(14)和(15)式成立且β1=0和g(x,t)≡0,那么存在ε0>0使得对每一个0<ε≤ε0,问题(12)和(13)的均方随机动力系统Φ在(Ω,F,{Ft}t∈R,P)上L4(Ω,F;H)中有唯一的弱D拉回均方随机吸引子A={A(τ):τ∈R}且对所有τ∈R有A(τ)=0.

证明因为β1=0和g(x,t)≡0,由(31)式,对每一个D={D(τ):τ∈R}∈D,可得

t→∞,

这表示0是Φ的一个D拉回弱吸引完全解.因此,由文献[32]中的定理2.6可得结论.