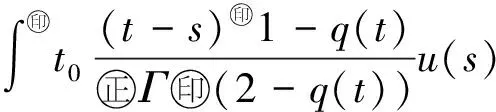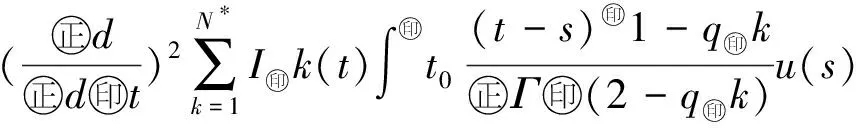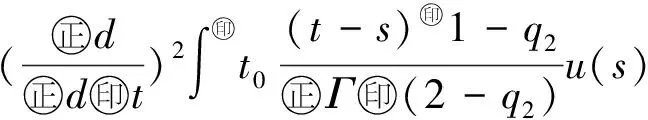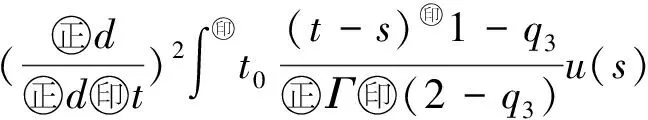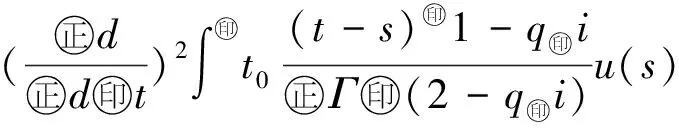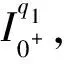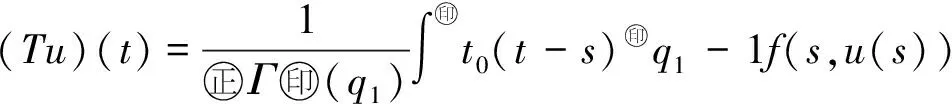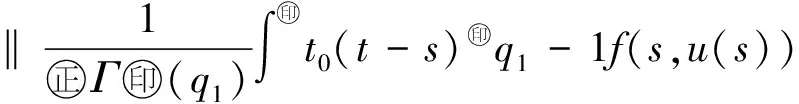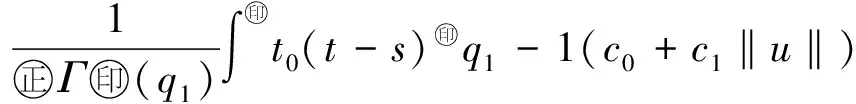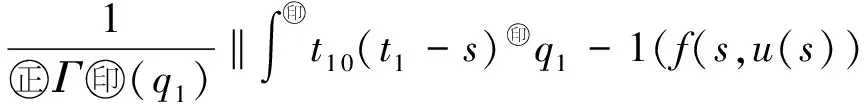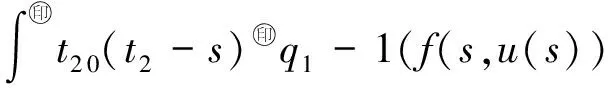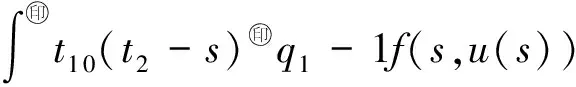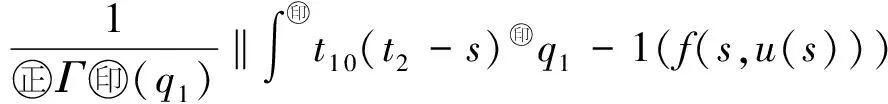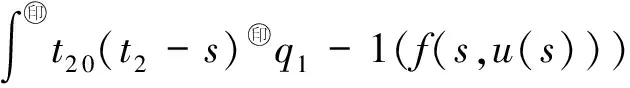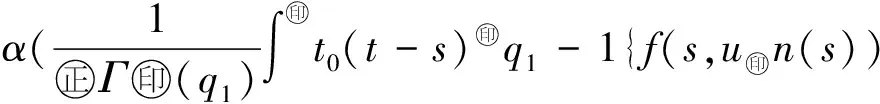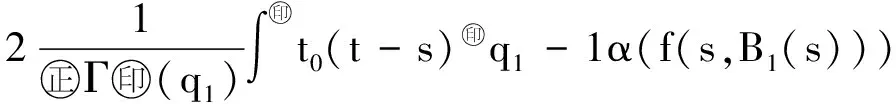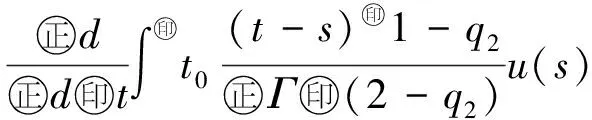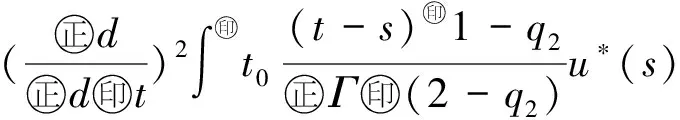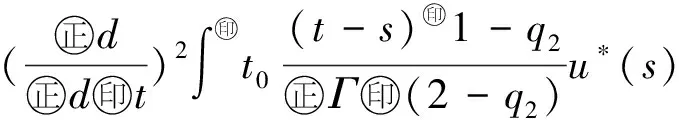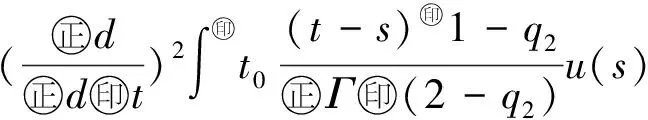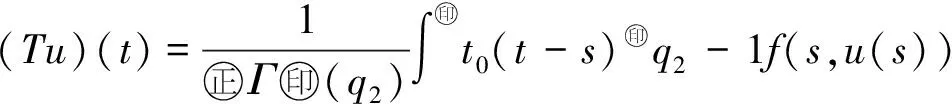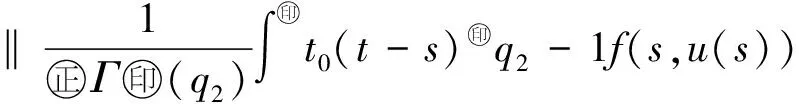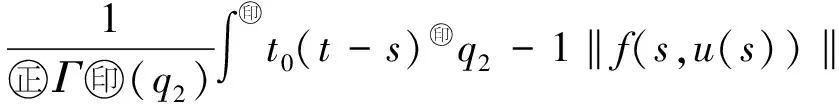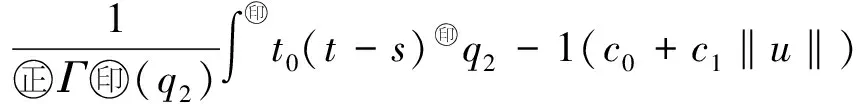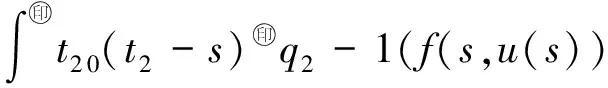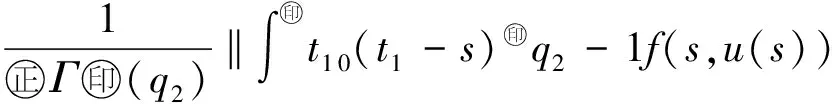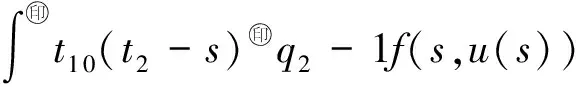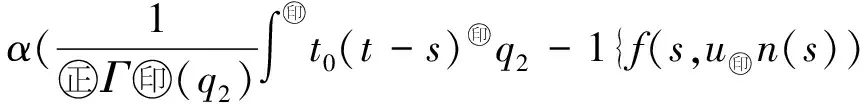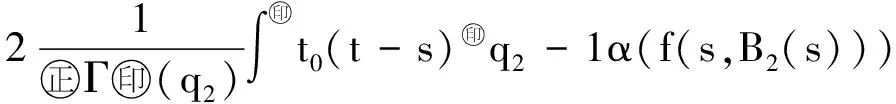Banach空间变阶数微分方程初值问题解的存在性
2022-05-13陈鹏玉
陶 书, 陈鹏玉
(西北师范大学 数学与统计学院, 甘肃 兰州 730070)
解的存在性,其中,是关于变阶q(t)的分数阶导数,函数f:J×E→E连续,J=[0,T].
近年来,分数阶微分方程在物理、化学、工程学等领域得到广泛应用.学者们利用Banach压缩映射原理,Krasnoselskii不动点定理、Schauder不动点定理等非线性泛函分析的工具获得了分数阶初边值问题解的存在性结果[1-9].文献[2]利用经典的分析方法,研究了分数阶微分方程初值问题
文献[9]利用上下解的单调迭代技巧,考虑实数空间R中分数阶微分方程初值问题
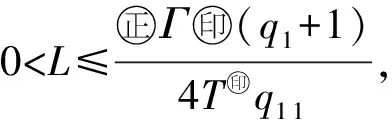
最近,文献[10]利用Banach压缩映射原理,研究了如下变阶数微分方程初值问题
Dds,t>0.
但上述所讨论的问题都局限在实数空间中,在Banach空间中对该类问题的研究相对较少.在一般的Banach空间中,常微分方程作为含无穷维参数的常微分方程及无穷维常微分方程组的抽象模型,是微分方程中一个重要研究课题[8-23].与普通的常微分方程相比较,抽象空间常微分方程的解算子不再具有紧性,为了对相应的解算子应用凝聚映射的拓扑度理论及相关的不动点定理,通常要给非线性项附加一些用非紧性测度描述的“紧性条件”.
受上述文献启发,本文将运用凝聚映射的不动点定理,在Banach空间E中讨论变阶数微分方程初值问题
(1)
1 记号和预备知识
设E为Banach空间,C(J,E)按范数
‖u‖C=maxt∈J‖u(t)‖
构成Banach空间.α(·)、αc(·)分别表示E、C(I,E)中的有界集Kuratowskii非紧性测度,对任意的B⊂C(J,E)和t∈J,记
B(t)={u(t)|u∈B}⊂E,
如果B在C(J,E)中有界,则B(t)在E中有界且α(B(t))≤α(B).
下面给出变阶数Riemann-Liouville型积分和微分的定义.
定义 1.1设
q(t):[a,b]→(0,+∞), -∞ Iq(t)ds,t>a, 定义 1.2设 q(t):[a,b]→(n-1,n), -∞ Dq(t) t>a, 命题 1.1[1]等式 成立,其中f∈L(a,b),0 命题 1.3[1]设α>0,那么微分方程 Dαa+u=0 有唯一解 u(t)=c1(t-a)α-1+c2(t-a)α-2+ …+cn(t-a)α-n, 其中 ci∈R,i=1,2,…,n,n-1<α≤n. 命题 1.4[1]设α>0,u∈L(a,b), 那么下面的等式成立 Iαa+Dαa+u(t)=u(t)+c1(t-a)α-1+ c2(t-a)α-2+…+cn(t-a)α-n, 其中 ci∈R,i=1,2,…,n,n-1<α≤n. Ip(t)a+Iq(t)a+f(t)≠Ip(t)+q(t)a+f(t), p(t)>0,q(t)>0,f∈L(a,b), -∞ 引理 1.1(Sadovskii不动点定理) 设E是Banach空间,U是E中的有界凸闭集,若T:U→U为凝聚映射,则T在U中有不动点. 定义 1.3[10]一个广义区间R的子集I,要么是一个区间([a,b],(a,b),(a,b],[a,b));一个点{a};或者是空集. 定义 1.4[10]如果I是一个广义区间,I的分割是包含在I中的广义区间的有限集P中,使得I中的每一个元素x正好位于P中的一个广义区间J中. 定义 1.5[10]设I是一个广义区间,设f:I→R是一个函数,P是I的一个分割,对于每一个J∈P,f是一个关于p的分段常数,f在J上是常数. 定义 1.6[10]设I是一个广义区间,函数f:I→R在I上称为分段常数,如果存在I的分割P,使得f是关于P的分段常数. 引理 1.2[12]设D⊂E有界时,则存在D的可数子集D0⊂D,使得 α(D)≤2α(D0). 引理 1.3[12]设B⊂C(J,E)有界且等度连续,则α(B(t))在J上连续,且 αC(B)=maxt∈JαC(B(t))=αC(B(J)). 引理 1.4[12]设B={un}⊂C(J,E)有界,则α(B(t))在J上可测,且 假设下列条件成立: (H1) 设P={[0,T1],(T1,T2],(T2,T3],…,(TN*-1,T]}(N*是给定的自然数)是有限区间[0,T]的一个分割,又设q(t):[0,T]→(1,2]是关于P的分段常数函数,即 其中,1 (H2) 存在常数c0,c1>0,使得 ‖f(t,u)‖≤c0+c1‖u‖, ∀t∈J,u∈E. (H3) 存在常数L,满足 使得对任意的t∈J及有界集D⊂E,有 α(f(t,D))≤Lα(D). 为了得到主要结论,首先对方程(1)进行分析.根据条件(H1),有 因此,可得到 (2) 方程(1)可写成 0 方程在[0,T1]可写成 0 (3) 方程在(T1,T2]可写成 T1 (4) 方程在(T2,T3]可写成 T2 (5) 同理,方程在(Ti-1,Ti],i=4,5,…,N*,(TN*=T)可写成 Ti-1 (6) 定义 2.1如果存在函数ui(t),i=1,2,…,N*,使得u1∈[0,T1]满足方程(3)且 t2-q1u1(0)=0; u2∈[0,T2]满足方程(4)且 t2-q2u2(0)=0; u3∈[0,T3]满足方程(5)且 t2-q3u3(0)=0; ui∈[0,Ti]满足方程(6)且 t2-qiui(0)=0,i=4,5,…,N*,TN*=T, 那么,方程(1)有一个解. 注 1如果定义2.1的函数ui(t)是存在的,则方程(1)至少存在一个解,i=1,2,…,N*. 根据前面的论证,有如下结果. 定理 2.2假设条件(H1)~(H3)成立,那么初值问题(2)在区间[0,T]上至少存在一个解u(t). 证明令Ui={u(t)|u(t)∈C[0,T], u(0)=0, ‖u(t)‖≤R, t∈[0,T](i=1,2,…,N*(TN*=T))}, u(t)=c1tq1-1+c2tq1-2+ 其中 t2-q1u(0)=0. 由方程(1)的初值条件和函数f的假设,可得 c1=c2=0. 定义算子T:C[0,T1]→C[0,T1], 0 (7) 则算子T在U1的不动点就是方程(3)的解. 对任意的u(t)∈U1,由于Tu(0)=u(0)=0,Tu(t)在[0,T1]上是连续的,由方程(7)得 ‖Tu(t)‖= 因此,T是U1映到U1的. 对任意的 u∈U1, ∀ε>0,t1,t2∈[0,T1],t1 取 那么当0 ‖(Tu)(t1)-(Tu)(t2)‖= (t2-s)q1-1]‖f(s,u(s))‖ds+ (c0+c1‖u‖)≤ 因此,TU1是等度连续的,显然也是一致有界的.令B⊂U1,由引理1.2知存在可数子集 B1={un}⊂B,n=1,2,…,N*, 那么由引理1.3有 α 对任意的t∈J,根据引理1.4可得 αC(T(B1(t)))= 根据非紧性测度的性质及条件(H3),有 α(f(s,B1(s))≤LαC(B1(s))≤ LαC(B1)≤LαC(B). 于是 αC(T(B1(t))≤ 2Lαds, 对该式两边取最大值,得 α αC(T(B))≤2αC(T(B1))< 从而T:U1→U1凝聚. 由Sadovskii不动点定理知,T在U1中有不动点且该不动点为方程(1)的解.方程(2)在区间(T1,T2]可改写成方程(4),为了考虑方程(4)解的存在性结果,可以讨论方程(4)在区间(0,T2]的定义 0 (8) 由此可见,如果函数u∈C[0,T2],满足方程(8),那么u(t)一定满足方程(4).事实上,如果 t2-q2u*∈C[0,T2] 是方程(8)的一个解,那么 Dq20+u*(t)= 0 (9) 且t2-q2u*(0)=0.因此,可以得到 T1 因此,u*∈C[0,T2]与t2-q2u*(0)=0满足方程 T1 u(t)=c1tq2-1+c2tq2-2+ 其中t2-q2u(0)=0.由方程(1)的初值条件和函数f的假设,可得 c1=c2=0. 定义算子T:C[0,T2]→C[0,T2], 0 (10) 则算子T在U2的不动点就是方程(4)的解. 对任意的u(t)∈U2,由于Tu(0)=u(0)=0,Tu(t)在[0,T2]上是连续的,由方程(10)得 ‖Tu(t)‖= 因此,T是U2映到U2的. 对任意的 u∈U2, ∀ε>0,t1,t2∈[0,T2],t1 取 那么当0 ‖(Tu)(t1)-(Tu)(t2)‖= 所以,TU2是等度连续的,显然也是一致有界的.令B⊂U2,由引理1.2知存在可数子集 B2={un}⊂B,n=1,2,…,N*, 那么由引理1.3有 αC(T(B2))=maxt∈JαC(T(B2(t))). 对任意的t∈J,根据引理1.4可得 αC(T(B2(t)))= 根据非紧性测度的性质及条件(H3),有 α(f(s,B2(s))≤LαC(B2(s))≤ LαC(B2)≤LαC(B). 于是 αC(T(B2(t))≤ 2Lαds, 对该式两边取最大值,得 α αC(T(B))≤2αC(T(B1)< 从而T:U2→U2凝聚. 由Sadovskii不动点定理知,T在U2中有不动点且该不动点为方程(1)的解. 同理,对于i=3,4,…,N*,得到定义在(Ti-1,Ti]的方程(2)有解xi(t)∈Ui和t2-qixi(0)=0,(TN*=T).因此,得到初值问题(1)至少存在一个解. 致谢西北师范大学参与式研讨课教学改革项目对本文给予了资助,谨致谢意.
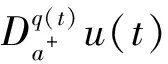
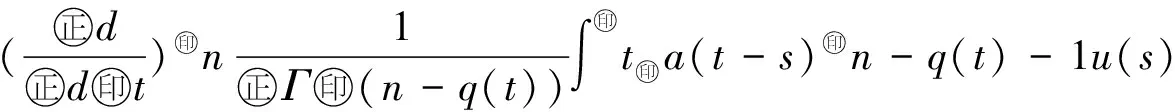
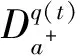
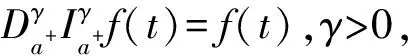
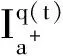
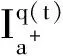
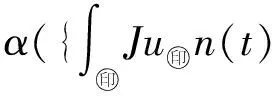
2 主要结果