折叠交叉超立方体的2-额外连通度和2-额外边连通度
2022-05-13郭慧媚阿依古丽马木提
郭慧媚, 阿依古丽·马木提
(新疆大学 数学与系统科学学院, 新疆 乌鲁木齐 830046)
现今,人们构建了各种各样的互联网络.通过互联网络交换信息的具有高性能的多处理器系统需随着实际生活的需要而被开发.一般来说,一个互联网络可以被视为一个无向图G=(V,E),V中的每一个顶点就代表一个处理器,E中的每一条边代表通信线路.连通度κ和边连通度λ通常是用来衡量网络可靠性和容错性的参数[1-2].然而,这两个参数只适用于一些互联网络.实际运用中的互联网络往往比较复杂,这两种测量的参数都有一些缺陷,因为与某一个出错的处理器邻接的所有处理器或与某一个出错的处理器关联的所有通信线路并不总是同时失去运行能力.为了克服这一缺陷并获得更准确的测量,推广经典的连通度的概念很有必要.Harary 是第一个对连接组件增加限制的人,他定义了条件连通度[3].
n-维的超立方体Qn是经典的互联网络.这个网络的许多性质已经被证明.当n≥3时,κ1(Qn)=2n-2;当n≥5时,κ2(Qn)=3n-5[5].当n≥3时,λ1(Qn)=2n-2;当n≥4时,λ2(Qn)=3n-4[6].折叠超立方体FQn是Qn的变体,首先由El-Amawy等[7]提出.文献[6,8]证明了当n≥4时,κ1(FQn)=2n;当n≥8时,κ2(FQn)=3n-2;当n≥5 时,λ2(FQn)=3n-1.Xu等[9]证明了当n≥2时,λ1(FQn)=2n.在1992 年,Kemal[10]定义了n-维交叉超立方体.Chen等[11]证明了当n≥4时,κ1(CQn)=λ1(CQn)=2n-2.Yang等[12]证明了当n≥4时,λ2(CQn)=3n-4;当n≥5时,κ2(CQn)=3n-5.在CQn和FQn的基础上,Zhang[13]在2002年定义了折叠交叉超立方体FCQn.比起前面的几种互联网络,折叠交叉超立方体具有更多良好的性质,比如:更短的直径、更短的平均节间距离,以及非常低的信息流量密度[14].最近,Cai等[15]证明了当n≥4时,κ1(FCQn)=λ1(FCQn)=2n.
本文主要证明了当n≥8时,κ2(FCQn)=3n-2;当n≥5时,λ2(FCQn)=3n-1.为了方便证明,在n+1维上讨论.
1 预备知识
本节介绍一些定义、引理以及标号.

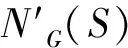
其中V(S)表示S中的顶点集,E(S) 表示S中的边集.图G的围长g(G)表示G中的最短圈.本文中所用到的标号和定义可以参考文献[1].
定义 1.1[16]两个二进制字符串u=u1u0和v=v1v0被称作是配对相关的,当且仅当它们满足
(u,v)∈{(00,00),(01,11),(11,01),(10,10)},
用符号u~v表示;若u和v不配对相关,表示为uv.
n-维交叉超立方体CQn有2n个顶点和n2n-1条边.关于CQn的定义如下.
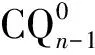
1) 若n是偶数,则un-2=vn-2;

CQn中的任意2个点u=un-1un-2…u0,v=vn-1vn-2…v0是邻接的当且仅当存在一个正整数l,1≤l≤n,使得下列4个条件同时被满足:
1)iun-2…ul=ivn-2…vl;
2)ul-1≠vl-1;
3) 若l是偶数,ul-2=vl-2;
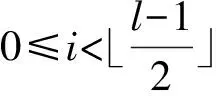
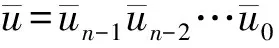
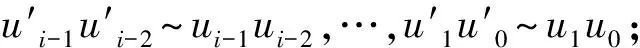
其中

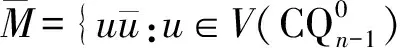
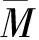
因此,可以将FCQn表示为
其中
V(FCQ
E(FCQ
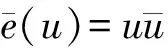
FCQ3和FCQ4如图1所示.
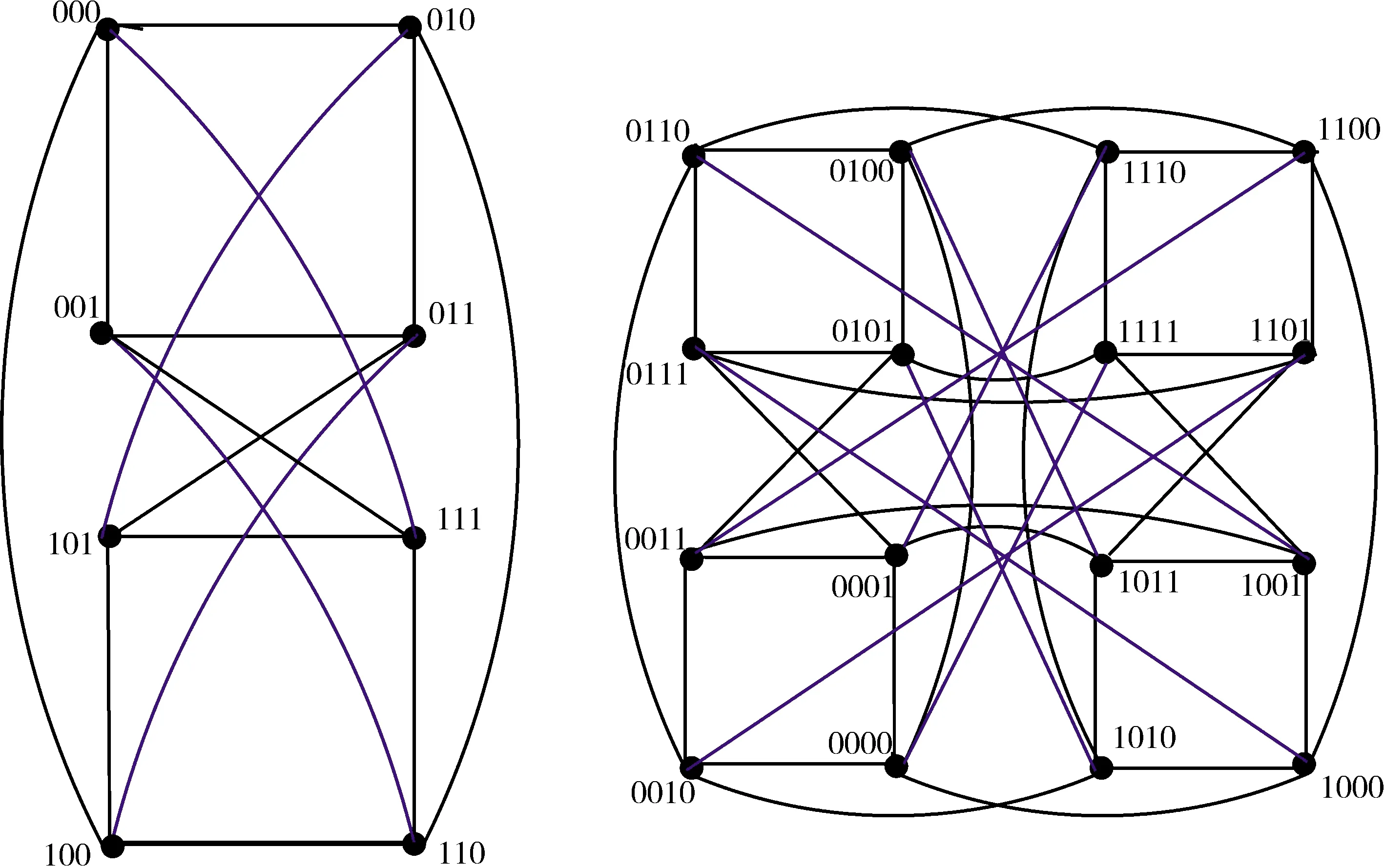
图 1 FCQ3与FCQ4
引理 1.4[16]κ(CQn)=λ(CQn)=n.
引理 1.5[11]当n≥3时,
κ1(CQn)=λ1(CQn)=2n-2.
引理 1.6[6,12]当n≥5时,κ2(CQn)= 3n-5;当n≥4时,λ2(CQn)= 3n-4.
引理 1.7[17]κ(FCQn)=λ(FCQn)=n+1.
引理 1.8[15]当n≥4时,CQn不含三圈.
引理 1.9[15]CQn中的任意2个点u和v最多有2个公共邻点,即|NCQn(u)∩NCQn(v)|≤2.
引理 1.10[16]CQn中的任意2个点u和v含有2个公共邻点当且仅当存在i、j满足0≤i 证明已知uiui-1∈{00,01,10,11},当 综上讨论,引理成立. 引理 1.12[15]FCQn中的任意2个不同的点u和v最多含有2个公共邻点,即 |NFCQn(u)∩NFCQn(v)|≤2. 引理 1.13[15]当n≥4时,FCQn中不含三圈. 引理 1.14FCQn中的任意一个点位于一个四圈中. 当i是偶数时,同样可以找到一个点v满足uj=vi,ui=vj,此时有 所以FCQn中的任意一个顶点u位于四圈uuivviu中,引理成立. 证明这个推论可以直接通过引理1.11以及对照表1~3得到,在这里不做过多赘述. 表 1 与u相关的点 表 2 与uiui-1相关的二进制字符串(I) 表 3 与uiui-1相关的二进制字符串(II) A={ui,(ui)n:i∈{0,1,2,…,n-1}}∩F, B={(uj)t,((uj)t)n:t∈{0,1,2,…,n-1},t≠j}∩F, C={(uk)i,((uk)i)n:i∈{0,1,2,…,n-1},i≠j,k}, |C∩F|≤|F-(A∪B∪D)|= 引理 2.2当n≥7时,κ2(FCQn+1)≤3n+1. 证明设C是FCQn+1中的四圈,P是这个四圈的二长路,显然|NFCQn+1(P)|=3n+1.接下来,将证明NFCQn+1(P)使FCQn+1不连通,并且FCQn+1-(NFCQn+1(P)∪P)是含有至少3个顶点的连通分支. 并且 2n-6-(3n-5)-3>2n-22(n+1)>4, |FCQn+1-(NFCQn+1(P)∪P)|≥3. 2n-(2n-1)-2-(n+2)-1>2n-22(n+1)>4, 通过上述分析,可以得到NFCQn+1(P)使FCQn+1不连通,FCQn+1去掉NFCQn+1(P)后剩下的每个连通分支都至少包含3个顶点,即 κ2(FCQn+1)≤3n+1. 引理 2.3当n≥7时,κ2(FCQn+1)≥3n+1. |F′|=|F1|+1<2n-3+1=2n-2=κ1(CQn), 则0≤|Q|≤n-6,而且Q中的顶点可能位于 当|F1|=n-6+2+n时,可以得到 |F0|≤3n-|F1|=n+4, 且|H|=n+5.当|F1|=n-7+2+n时,可以得到 |F0|≤3n-|F1|=n+5, 因此,当|F|≤3n,且FCQn+1-F既不包含孤立点也不包含孤立边时,FCQn+1-F是连通的.即当n≥7时,κ2(FCQn+1)≥3n+1. 定理 2.4当n≥7时,κ2(FCQn+1)=3n+1. 引理 2.6当n≥4时,λ2(FCQn+1)≤3n+2. 证明在FCQn+1中,设P是一条二长路,那么 引理 2.7当n≥4时,λ2(FCQn+1)≥3n+2. |F1|<2n-2=λ1(CQn), 则 |B∩F|≤3n+1-n-n-3=n-2. 综上所述,当|F|≤3n+1,FCQn+1-F既不包含孤立点,也不包含孤立边时,可以得到FCQn+1-F是一个连通分支.即当n≥4时,λ2(FCQn+1)≥3n+2. 定理 2.8当n≥4时,λ2(FCQn+1)=3n+2. 本文探究了n-维折叠交叉超立方体FCQn的2-额外连通度和2-额外边连通度.FCQn是具有许多良好性质的网络.证明当n≥8时,κ2(FCQn)=3n-2;当n≥5时,λ2(FCQn)=3n-1.也就是说,当n≥8时,至少要去掉3n-2个顶点,当n≥5时,至少要去掉3n-1条边,使得FCQn不连通,并且剩下的每个连通分支至少有3个顶点.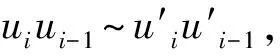


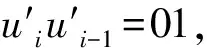
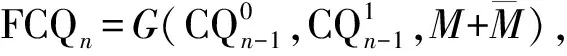
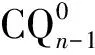
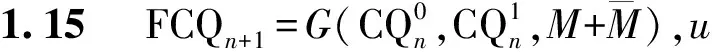




2 主要结果
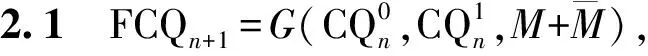
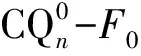


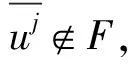

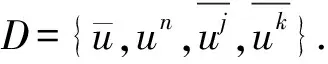
|F|-|A|-|B|-|D|≤n-3.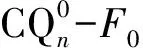
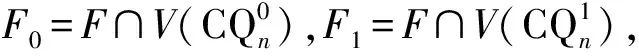
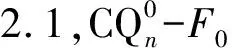
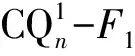

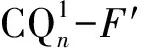






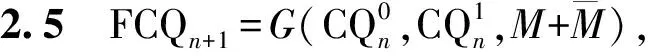

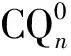
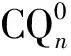
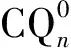
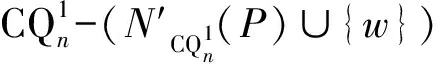
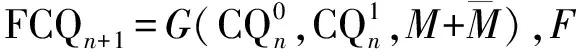

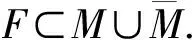





3 结论
